复杂赋存形态水合物储层地震岩石物理建模与应用

潘豪杰，李勇根，魏超，桂志先，李晓明，张翔*，赵懿，张伟

1 长江大学地球物理与石油资源学院，武汉 430100 2 中国石油勘探开发研究院，北京 100083 3 中国石油华北油田勘探部，河北任丘 062552 4 中国石油集团测井有限公司华北事业部，河北任丘 062552

0 引言

天然气水合物是由天然气和水在高压低温条件下形成的笼状晶体化合物，广泛分布于陆域永久冻土带和大陆边缘深水盆地的沉积物中（Kvenvolden,1993）.水合物因其能量密度高、储量规模大、埋藏深度浅、分布范围广和开发前景好而被誉为继煤层气、致密油气和页岩油气之后最具潜力的替代能源（宁伏龙等,2020；文鹏飞等，2021）.然而，水合物的分解又会诱发海洋地质灾害和引起全球气候变化（Riedel et al.,2010）.因此，预测水合物含量和空间展布规律具有重要的科学意义和实用价值.

天然气水合物的存在往往会显著地改变地震波速度、衰减、电阻率、渗透率和剪切强度等基本物理性质（Best et al.,2013;Konno et al.,2015;Yoneda et al.,2019;裴发根等，2020；Ren et al.,2020;Zhang et al.,2021）.然而，这些岩石物理特性变化的幅度不仅与水合物饱和度有关，也与水合物赋存模式密切相关（Ojha et al.,2010）.这种水合物赋存形态和饱和度之间的耦合影响会引起地球物理响应特征的非均匀变化，致使水合物储层的地球物理表征存在多解性和不确定性.此外，受地质与地球物理条件的影响，水合物在实际地层中赋存形态复杂多样、多种模式共存，导致水合物资源量精细评价面临着巨大的挑战.

水合物饱和度的准确预测依赖于可靠的赋存形态信息.为了表征水合物在孔隙空间中的微观赋存模式，许多学者先后提出了取样岩心观察（Holland et al.,2008）、X射线CT 扫描分析（Chaouachi et al.,2015;Sahoo et al.,2018）、电阻率成像测井（Cook et al.,2008）、速度与密度组合敏感因子（Liu and Liu,2018）、纵波速度和电阻率交会模版（Lee and Collett,2009）以及纵横波速度（或衰减）与水合物饱和度交会图版（Dai et al.,2004;Zhan and Matsushima,2018）等识别方法.一般地，取芯分析技术的岩心保真难、取样成本高、覆盖范围小，而且基于该方法识别的水合物产状特征（如块状、脉状和层状等）难以直接建立与地球物理响应特征之间的量化关系.电阻率成像是定性识别孔隙充填和裂缝充填型水合物的有效手段，但其垂向分辨率低且不适用于低角度（<10°）裂缝的识别（Cook et al.,2008;Collett et al.,2019）.与定性识别方法不同，速度与密度组合敏感因子和纵波速度与电阻率交会图版是以岩石物理模型为基础，利用弹性和电性响应特征的差异实现孔隙充填型和裂缝充填型水合物的半定量识别，但其无法区分骨架支撑和胶结等其他赋存形态（Liu and Liu,2018）.纵横波速度（或衰减）与水合物饱和度的交会图版通常能识别水合物的主导赋存形态（Dai et al.,2004;Zhan and Matsushima,2018），但难以合理判识复杂水合物赋存形态.再者，利用不同测量数据（渗透率、速度、电阻率等）识别的主要赋存形态可能差异较大（Yoneda et al.,2019）.因此，亟需发展复杂赋存形态和水合物饱和度同步预测技术，以提高赋存形态识别和水合物饱和度预测的精度.

地震岩石物理模型建立了水合物储层微观结构、物性参数与弹性响应特征之间的量化关系，为厘清水合物饱和度和赋存形态对水合物储层弹性性质的影响奠定了理论基础.目前，国内外许多学者提出了一系列用于计算岩石弹性模量和预测水合物饱和度的岩石物理模型，大致可分为：颗粒有效介质模型、包含物模型和孔隙弹性理论模型.以胶结模型（Dvorkin and Nur,1996）和接触模型（Helgerud et al.,1999）为主的颗粒有效介质模型通常将沉积物颗粒视为理想弹性球的随机集合体，水合物视为胶结物或孔隙充填物，基于颗粒之间的应力与应变关系推导接触刚度和弹性模量，预测的剪切模量和横波速度往往偏高.常用的包含物模型是三相或四相Kuster-Toksöz模型（Lee et al.,1996）和自相容-微分等效介质模型（SCA-DEM）（Jakobsen et al.,2000;Chand et al.,2006;Liu et al.,2018）.前者将球形沉积物颗粒视为包含物，加入到以水合物和水组成的背景基质中，利用迭代方法计算地层有效弹性模量，适用于高孔隙度（超过80%）的水合物地层；后者考虑了水合物和沉积物颗粒的微观结构及其连通性，然而水合物充当包含物和沉积物颗粒一部分时预测的不含水合物地层速度差异很大（Chand et al.,2006）.孔隙弹性理论主要是考虑了沉积物颗粒、水合物和孔隙流体之间的相互作用对水合物地层整体弹性性质的影响，这方面代表性的模型包括改进的Biot-Gassmann理论（BGTL）（Lee,2002）和简化三相方程（STPE）（Carcione and Gei,2004;Lee and Waite,2008）.BGTL模型基于经典Biot-Gassmann方程计算体积模量，利用沉积物速度比与基质速度比之间的关系修正剪切模量，但需要有实验或者测井数据等对各种经验参数进行标定；STPE模型利用改进的Lee-Pride模型（Pride et al.,2004）计算干岩石模量，该方程更适合于含水合物的砂岩储层而非富泥质储层.此外，这些岩石物理模型在实际应用时简化了赋存形态假设，主要针对各向同性或弱各向异性含单一赋存形态水合物储层，难以合理表征各向异性复杂赋存形态水合物储层弹性响应模式.因此，需要根据实际储层矿物、水合物赋存形态及孔隙流体特征选择合适的理论支撑，使岩石物理建模结果能够逼近实际水合物储层特征.

本文针对复杂赋存形态水合物地层，基于边界平均模型、包含物模型、广义有效介质模型和孔隙弹性理论等，建立了同时含六种赋存形态水合物储层岩石物理模型.通过数值模拟分析了不同赋存形态和水合物饱和度对岩石弹性特性的影响，结合声学实验数据验证了所建模型的有效性和可靠性，利用冻土区水合物测井数据测试了单一和多重赋存形态对饱和度预测精度的影响，联合海域水合物纵横波速度和密度测井数据预测了水合物饱和度和赋存形态百分比，为水合物储层地震精细刻画提供重要的理论和技术支撑.

1 多重赋存形态水合物岩石物理建模

按照水合物与沉积物颗粒之间的微观结构特征，Dai等（2004）系统总结了六种水合物微观分布模式：接触胶结、颗粒包裹、骨架支撑、孔隙充填、基质与包含物共存和结核/裂隙充填形态（图1）.然而，不同赋存形态的水合物影响岩石弹性性质的方式存在一定差异.一般地，占据孔隙空间的接触胶结和颗粒包裹型水合物固结沉积物颗粒、降低地层孔隙度并增强沉积物刚度；骨架支撑和基质与包含物共存型水合物可视为固体基质的一部分，降低地层孔隙度并增加岩石基质的弹性模量；孔隙充填型水合物只改变孔隙流体的体积模量而不影响岩石基质模量；结核/裂隙充填型水合物使沉积物颗粒分离，并逐渐形成含水合物的结核和裂隙等，使得水合物地层具有各向异性特征（Lee and Collett,2009）.依据上述六种微观赋存形态水合物对弹性模量影响机制的差异性，选用不同的岩石物理理论构建复杂赋存形态水合物储层岩石物理等效模型.具体岩石物理建模流程包括以下四部分（图2）：（1） 岩石基质模量计算；（2） 干岩石骨架模量计算；（3） 流体饱和岩石模量计算；（4） 各向异性水合物地层速度计算.

1.1 岩石基质模量计算

假设骨架支撑型水合物与沉积物颗粒相结合组成固体基质，共同起到应力支撑作用.在已知各种矿物组分的体积分数和弹性模量时，通过Voigt-Reuss-Hill（Hill,1952）平均模型可以计算固体基质体积模量和剪切模量：

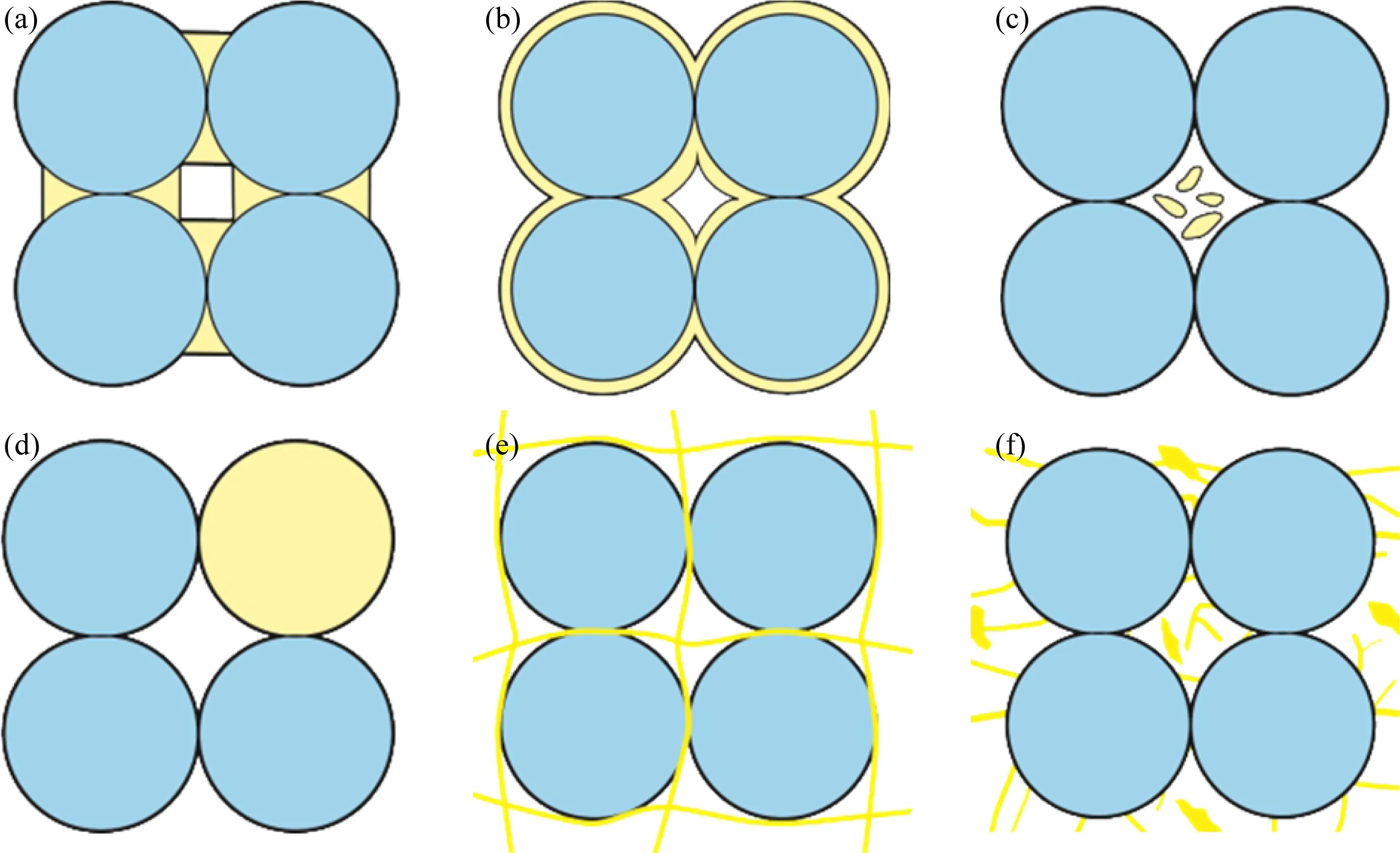
图1 六种天然气水合物赋存形态（a） 接触胶结；（b） 颗粒包裹；（c） 孔隙充填；（d） 骨架支撑；（e） 基质与包含物共存；（f） 结核/裂隙充填.Fig.1 Six basic hydrate morphologies（a） Contact-cementing;（b） Grain-coating;（c） Pore-filling;（d） Matrix-supporting;（e） Matrix-inclusion;（f） Fracture-filling.

（1）

（2）

式中：Ks、Kh和μs、μh分别为固体矿物和水合物的体积模量和剪切模量；骨架支撑型水合物的体积为φh=φγmsSgh,φ,γms和Sgh分别为孔隙度，骨架支撑形态百分比和水合物饱和度.由于骨架支撑型水合物的存在，孔隙度将会降低为φr=φ（1-γmsSgh）.值得注意的是，当不含骨架支撑型水合物（γms=0）时，公式（1）和（2）计算结果为固体矿物基质模量.

图2 复杂赋存形态水合物储层岩石物理建模流程Fig.2 Rock physics modeling of the complex-morphology hydrate reservoirs

考虑基质与包含物共存型水合物与沉积物颗粒间的连通性以及孔隙结构对水合物储层弹性性质的影响，采用各向同性SCA-DEM弹性模型（Han et al.,2012;Attias et al.,2020）计算基质与包含物共存型水合物和固体基质混合得到的岩石基质弹性模量.首先，利用SCA模型计算这两相介质体积含量均为50%条件下岩石基质的弹性模量：

0.5（Kh-KSCA）P*h+0.5（Km-KSCA）P*m=0，

（3）

0.5（μh-μSCA）Q*h+0.5（μm-μSCA）Q*m=0，

（4）

其中KSCA和μSCA分别为SCA模型计算的等效体积模量和剪切模量,P*h、Q*h和P*m、Q*m对应水合物和固体基质时的极化因子.

然后，将SCA模型计算的岩石基质弹性模量作为DEM模型迭代求解的初始值，通过DEM模型将水合物和固体基质的体积含量分别调整至实际值：

（5）

（6）

Kma=KDEM，

（7）

μma=μDEM，

（8）

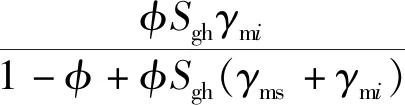
1.2 干岩石骨架模量计算

为了考虑接触胶结和颗粒包裹两种赋存形态水合物对干岩石骨架模量的影响，Pan等（2020a）引入压力相关的广义接触胶结半径并提出了改进的胶结模型，表达式为：

（9）

（10）

（11）

（12）

（13）

为了解决经典的胶结模型与Hashin-Shtrikman-Hertz-Mindlin模型无法耦合的问题，Pan等（2020b）在改进的胶结模型基础上利用Hashin-Shtrikman界限进行约束提出了广义有效介质模型，具体公式为：

（14）

（15）

1.3 流体饱和岩石模量计算

将孔隙充填型水合物视为孔隙流体的一部分，只考虑其对孔隙流体体积模量的影响.假设孔隙充填型水合物、游离气和水均匀分布在孔隙空间中，则孔隙流体体积模量可利用Wood公式（Wood,1941）计算得到：

（16）

在确定出岩石基质弹性模量、干岩石骨架弹性模量和孔隙流体体积模量后，依据Gassmann方程（Gassmann,1951）可计算饱和岩石的体积模量和剪切模量：

（17）

μsat=μdry，

（18）

式中，φe=φ[1-（γhc+γms+γmi）Sgh]为有效孔隙度.

当孔隙流体呈斑块分布时，饱和岩石的体积模量由Hill理论（Hill,1963）计算：

（19）

其中完全水合物饱和、水饱和和气饱和体积模量分别为：

（20）

（21）

（22）

1.4 各向异性水合物地层速度计算

Lee和Collett（2009）将裂隙充填型水合物地层简化为多层完全水合物饱和裂隙和完全水饱和沉积物所构成的横向各向同性层状介质，结合简化三相方程和Backus平均（Backus,1962;王吉亮等,2013））推导了层状介质模型.在此模型假设基础上，采用Gassmann方程或者Hill方程计算各向同性不含裂隙沉积物的弹性参数，利用Backus平均计算各向异性水合物储层的纵横波速度，公式为：

（23）

（24）

（25）

（26）

（27）

ρb=〈ρ〉，

（28）

（29）

（30）

（31）

（32）

2 理论模拟分析

采用上述岩石物理建模方法，定量分析水合物饱和度和赋存形态对纵横波速度、泊松比和纵横波速度比的影响.假设水合物地层矿物组分由50%黏土和50%石英组成，孔隙度为0.4，孔隙流体由水合物和水均匀分布在孔隙空间中，临界孔隙度、配位数、滑动摩擦系数、包含物纵横比和有效压力分别设定为0.39，8，1.0，0.9和5 MPa.表1给出了数值计算所用的各组分弹性模量和密度.

表1 数值计算所用的各组分弹性模量和密度Table 1 Elastic moduli and densities for the mineral components

图3展示了不同赋存形态水合物地层纵横波速度、泊松比和纵横波速度比随水合物饱和度的变化特征.所有赋存形态水合物地层纵横波速度均随水合物饱和度增大而增加，但不同赋存形态水合物地层速度随水合物饱和度的变化趋势差异较大.对于接触胶结和颗粒包裹模式，纵横波速度在低饱和度（<5%）时迅速增加，然后在高饱和度时缓慢增加.然而，这两种赋存模式的水合物地层泊松比和速度比与水合物饱和度之间的关系比较复杂.泊松比和速度比均是先减小，当超过临界水合物饱和度时快速增加.这一现象主要是因为少量水合物可以固结沉积物颗粒，而大量水合物则在颗粒接触处或颗粒表面形成水合物薄膜，降低地层刚度.假设孔隙充填型水合物只影响孔隙流体的体积模量，纵波速度、泊松比和纵横波速度比均随水合物饱和度呈线性增加，横波速度因水合物替换孔隙水引起密度的微弱降低而略微增加.由于骨架支撑型和基质与包含物共存型水合物均被视为固体基质一部分且充当应力承载作用，纵横波速度均随水合物饱和度增加而增加，然而泊松比和速度比随水合物饱和度增加而减小.随着水平和垂直裂隙充填型水合物饱和度增加，纵横波速度缓慢地增加，而泊松比和速度比逐渐降低.

图3 不同赋存形态水合物地层纵波速度（a）、横波速度（b）、泊松比（c）和纵横波速度比（d）与水合物饱和度的变化关系Fig.3 The relationships between hydrate saturation and P-wave （a）,S-wave （b）,Poisson′s ratio（c） and VP/VS ratio （d） of hydrate reservoirs for different morphologies

上述数值模拟结果显示，不同赋存形态水合物地层弹性参数对水合物饱和度的敏感性有所差异，这为水合物赋存形态识别提供了重要的启示.胶结型（颗粒包裹和接触胶结）水合物在低饱和度时与非胶结型水合物在高饱和度时可能具有相同的纵横波速度，这使得利用纵横波速度识别水合物形态存在多解性.与其他水合物地层不同的是，胶结型水合物地层泊松比和速度比随饱和度先减小再增加的特征，为判识胶结型水合物奠定基础.值得注意的是，只有孔隙充填型水合物地层纵波速度、泊松比和纵横波速度比随着水合物饱和度增加而增加，这为识别孔隙充填型水合物提供了理论依据.综合分析不同弹性参数随水合物饱和度的变化趋势，可以为水合物赋存形态识别和饱和度预测提供针对性指导.

3 实验数据测试

水合物声学实验为揭示水合物出现机制、赋存形态演化以及物理特性变化提供了重要的规律性认识.大量的甲烷和四氢呋喃（THF）水合物合成实验测量了不同温压、频率、岩性和合成方法下的声学响应特征参数，为检验岩石物理模型可靠性提供了数据支撑.选取4套在“富气”和“富水”环境下测量的甲烷和THF水合物合成实验声学数据，验证多重赋存形态水合物岩石物理建模方法的有效性（Priest et al.,2005,2009;Dugarov et al.,2019）.通过拟合实验数据与理论模拟曲线，可以确定临界孔隙度、配位数、滑动摩擦系数、孔隙纵横比和有效压力分别为0.38，8，0.4，0.9和5 MPa.数值计算所用到的弹性常数见表1.

图4比较了岩石物理模拟的纵横波速度与声学实验数据.从图中可以看出，在“富气”环境下测量的实验数据大多落在接触胶结和颗粒包裹模型曲线之间，而在“富水”环境下测量的实验数据介于孔隙充填和骨架支撑模型曲线之间.这表明水合物在砂岩中可能以多种赋存形态共存，且在“富气”环境下水合物主要以胶结模式（接触胶结和颗粒包裹）出现，而在“富水”环境下水合物主要以非胶结模式（骨架支撑和孔隙充填）出现.这与前人研究结论一致，即在“富气”环境下，水合物从水所在的颗粒接触处开始形成，然后随着水合物含量增加覆盖颗粒表面进而填充孔隙空间（Priest et al.,2005;Kingston et al.,2008;Cook and Waite,2018）；在“富水”环境下，水合物从气泡所在的孔隙位置开始形成，然后随着水合物含量增加形成水合物颗粒支撑沉积物颗粒（Yun et al.,2005;Kingston et al.,2008）.总体上说，水合物声学响应特征模拟可以捕捉水合物赋存模式及其演化规律，但仍难以确定水合物赋存形态之间相互转化时所对应的临界水合物饱和度.

图4 比较理论模拟与实验测试结果（a） 纵波速度；（b） 横波速度.Fig.4 Comparison of theoretical modeling and experimental data（a） P-wave;（b） S-wave.

4 实际数据应用

选取代表性的加拿大Mackenzie三角洲地区的Mallik 2L-38井、日本Nankai海槽AT1-MC井及新西兰北部Hikurangi边缘U1518B井来验证所建岩石物理模型的有效性和可靠性.其中，Mallik 2L-38井的数据用于分析不同赋存形态对水合物饱和度预测精度的影响；AT1-MC井和U1518B井的纵横波和密度数据用于水合物饱和度和赋存形态的同步定量预测.

4.1 水合物饱和度估算

1998年日本石油公司、日本国家石油集团和加拿大地质调查局在Mackenzie河三角洲的Mallik区域进行了天然气水合物钻探项目，通过钻井资料、测井数据和取芯岩样推测在897～1110 m井段存在天然气水合物（Miyairi et al.,1999）.因此，选取890～1110 m深度段作为水合物饱和度预测研究目的层.图5显示了测井解释的水合物饱和度、孔隙度和泥质含量等物性参数与纵横波速度和密度等测量数据.从图5可以看出，高饱和度水合物主要富集在897～923 m、950～1000 m、1005～1030 m和1075～1110 m等四个深度段的粗粒砂岩中.我们使用上述建模流程对Mallik 2L-38井897～1110 m井段进行各向同性水合物储层岩石物理建模，给定权重胶结系数Wc=0.2，临界孔隙度φc=0.38，配位数n=8.5，滑动摩擦系数τ=0.2，包含物纵横比α=0.4（Chand et al.,2006;Terry and Knapp,2018），以纵横波速度为约束，利用快速模拟退火算法预测不同赋存形态的水合物饱和度.

图6对比了接触胶结、颗粒包裹、孔隙充填、骨架支撑、基质与包含物共存等五种单一形态和多重赋存形态（γhc:γms:γpf=10%:75%:15%）下纵横波速度的预测值与实测值.可以观察到，考虑不同赋存形态利用所建模型计算的纵波速度整体与实测值吻合良好，而横波速度预测值与实测值在950～995 m和1070～1110 m（虚线框部分）之间吻合程度不同.骨架支撑型、基质与包含物共存型和多重赋存模式下横波速度预测相对比较精确，而接触胶结、颗粒包裹和孔隙充填模式下的横波速度预测误差较大.这也侧面反映了Mallik 2L-38井的粗粒砂岩层段中以骨架支撑型水合物为主且含有少量胶结型和孔隙充填型水合物.

图7为考虑不同赋存形态应用本文所建模型计算的水合物饱和度.由图可知，利用纵横波速度均可以获取不同赋存形态所对应的水合物饱和度，但是预测精度存在一定差异.对比观察六种赋存形态水合物饱和度预测值（尤其是虚线框部分），接触胶结型和颗粒包裹型水合物饱和度的估算值都略低于电阻率计算的水合物饱和度参考值；孔隙充填型和基质与包含物共存型水合物饱和度估算值都明显高于参考值；骨架支撑型水合物饱和度略高于参考值；而多重赋存形态水合物饱和度预测值与参考值总体吻合较好，这表明考虑多重赋存形态较单一形态预测精度更高，并揭示了该区域是以骨架支撑型水合物为主，并伴随有混合胶结型和孔隙充填型水合物共同富集于粗粒砂岩中.

图7 六种赋存形态下纵横波速度的预测结果与实测结果对比Fig.7 Comparisons of measured and estimated P- and S-wave velocities for six hydrate modes

图8 不同赋存形态水合物饱和度预测值与电阻率解释饱和度对比Fig.8 Comparison of hydrate saturation estimates for six hydrate morphologies and resistivity-based hydrate saturation

图8从统计分析的角度直观展示了四段粗粒砂岩中不同赋存形态水合物饱和度的预测精度.如图8所示，多重赋存形态水合物饱和度预测值与参考值相关性最强，预测结果的精度最高；接触胶结和颗粒包裹模式预测的饱和度明显偏低，而孔隙充填、骨架支撑和基质与包含物共存模式预测的饱和度明显偏高.这表明水合物岩石物理建模中耦合多种赋存形态可以更逼近真实储层特征，预测的水合物饱和度精度更高.

4.2 水合物饱和度和赋存形态同步预测

与4.1节通过给定多重赋存形态百分比预测水合物饱和度不同，本节聚焦水合物饱和度和多重赋存形态同步量化表征，以降低赋存形态对饱和度预测精度的影响.对研究井位的取芯分析和测井解释表明，AT1-MC井的水合物以孔隙充填、骨架支撑和胶结模式富集于粗粒砂岩储层的孔隙空间（Ito et al.,2015;Konno et al.,2015），而U1518B井的水合物以孔隙充填、骨架支撑和裂隙充填模式赋存于细粒粉砂或粉砂质黏土的孔隙和裂隙空间（Cook et al.,2020;Pan et al.,2020a,b）.依据这一赋存形态假设，仿照Pan等（2020a,b）和杨文强等（2021）的思想，结合所建岩石物理模型和快速模拟退火算法同步预测水合物含量和分布.岩石物理模型所用的组分参数见表1，其他模型参数如表2所示.

表2 AT1-MC井和U1518B井岩石物理建模所用模型参数Table 2 Model parameters used in the calculation at Site AT1-MC and Hole U1518B

图9为应用上述同步预测方法从AT1-MC井的纵横波速度和密度数据中反演得到的混合胶结、孔隙充填和骨架支撑形态百分比及水合物饱和度.从图中可以看出，计算的纵横波速度和密度与实测值吻合度非常高，而且水合物饱和度预测值与电阻率和核磁共振-密度测井解释及岩心测试分析的水合物饱和度也吻合较好.在275～334.9 m层段，预测的水合物饱和度最大值为95%，高于阿尔奇公式计算的最高饱和度84.1%和核磁共振-密度测井估算的最高饱和度68.2%；但估算的平均饱和度36.8%，介于阿尔奇公式计算的平均值46.03%和核磁共振-密度解释的平均值33.68%之间.造成部分预测值与解释结果之间存在差异的主要原因有两个：（1） 声波测井的分辨率低于核磁共振测井及电阻率测井的分辨率，使得纵横波速度无法准确预测出富集于274～286 m薄互层中的水合物含量；（2） 声波测井与电阻率和核磁共振测井存在深度偏移问题，使得相同幅值所对应的深度不一致.预测的赋存形态百分比显示，高饱和度（大于40%）水合物倾向于以骨架支撑形态分布在孔隙空间中，而中低饱和度水合物则以孔隙充填形态存在，同时伴随有少量的胶结形态出现.这一结果与Konno等（2015）的研究结论相一致，即在Nankai海槽粗粒砂岩层段中的水合物主要以骨架支撑型产出.水合物饱和度和赋存形态百分比预测结果的准确性和合理性验证了所建模型的有效性.

图9 AT1-MC井声波和密度反演的水合物饱和度与混合胶结、骨架支撑和孔隙充填体积比Fig.9 Simultaneous quantification of hydrate saturation and the fractions of hybrid-cementing,matrix-supporting and pore-filling from the sonic and density logs of AT1-MC well

图10展示了利用U1518B井的纵横波速度和密度数据预测孔隙充填、骨架支撑和裂隙充填形态百分比及水合物饱和度.结果显示，计算的纵横波速度和密度与实测值具有较好的一致性，尤其是低频趋势上趋于一致.在深度超过304.5 m出现纵横波速度和密度较浅层明显降低的现象，这主要是紧临Ppaku断层带（304.5～361 m），断裂和裂隙比较发育、地层变形强烈等因素导致的（Saffer et al.,2019）.在228～338 m深度段中，预测的水合物饱和度平均值为5.57%，局部高达27.3%.与电阻率和压力岩芯结果吻合相对较好，局部差异可能与测井仪器探测分辨率、测量深度偏移以及裂缝诱导的各向异性等因素相关.从图10中可以看到，相对高饱和度（大于8%）的水合物主要以骨架支撑形态分布在孔隙空间中，而相对低饱和度的水合物主要以裂隙充填形态为主，同时伴随有少量孔隙充填型水合物.这与Cook等（2020）的研究结论比较一致，即U1518区域形成的水合物是由微生物成因气局部扩散而非沿着断层长距离运移形成，主要分布在粗粒沉积物的孔隙空间而非结核和裂隙中.

图11对比了AT1-MC井和U1518B井的水合物赋存形态百分比均值.对于AT1-MC井，混合胶结、孔隙充填和骨架支撑型水合物百分比均值依次为4%，49%和47%，揭示高饱和度水合物倾向于以混合胶结、孔隙充填和骨架支撑等模式分布于粗粒砂岩孔隙空间中.对于U1518B井，孔隙充填、骨架支撑和裂隙充填型水合物百分比均值依次为8%，51%和41%，表明中低饱和度水合物常以孔隙充填、骨架支撑和结核/裂隙充填等形态赋存于薄砂层或粉砂层的孔隙和裂隙空间中.这一特征证实了沉积物岩性和颗粒大小是水合物形成和分布的主控因素.

5 结论

本文针对复杂赋存形态水合物地层，依据不同赋存模式的水合物对岩石弹性模量影响方式差异性，采用各种有效介质理论逐级耦合各类矿物组分、不同赋存形态水合物及孔隙流体等特征，构建了含六种赋存形态水合物储层岩石物理模型，厘清了水合物饱和度和赋存形态与弹性响应特征之间的量化关系，结合实验测量数据和冻土带及海域水合物测井数据验证了所建模型的可靠性和合理性，取得了较好的实际应用效果.在数值模拟方面，模拟了不同赋存形态下水合物饱和度对地层弹性响应特征的影响，为赋存形态准确识别奠定基础.此外，实验数据测试结果表明所建模型可以很好地捕捉不同形成环境下的水合物声学响应特征，识别水合物赋存形态并揭示其演化机制.对比速度计算的不同赋存形态水合物饱和度与电阻率解释结果发现，考虑多重赋存形态的岩石物理建模可以更逼近实际水合物地层，有效提高水合物饱和度预测准确性.另外，水合物饱和度和赋存形态同步量化表征方法不仅提高了水合物饱和度预测精度，而且揭示了水合物微观赋存特征，为水合物含量和空间展布规律的地震预测提供了重要的理论和技术支撑.

图10 U1518B井声波和密度反演的水合物饱和度与骨架支撑、孔隙和裂隙充填体积比Fig.10 Simultaneous quantification of hydrate saturation and the fractions of matrix-supporting,pore- and fracture-filling from the sonic and density logs of U1518B well

图11 基于AT1-MC和U1518B井数据预测不同水合物赋存形态百分比均值对比Fig.11 Comparison of the average proportions of different morphologies estimated from wells AT1-MC and U1518B