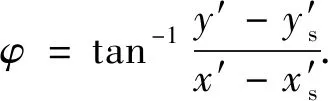随钻超深前视电阻率测井二次场耦合势三维有限体积法高效数值仿真

王亚洲，汪宏年*,莫修文，康庄庄，殷长春

1 吉林大学物理学院计算方法与软件国际中心,长春 130012 2 吉林大学地球探测科学与技术学院,长春 130026

0 引言

目前,随钻电磁波测井已经成为一种重要测井方法（Bell et al.,2006;Seydoux et al.,2014）,是进行地质导向、油水层识别和含油饱和度计算等工作的重要工具.常规随钻电磁波测井中采用的线圈系收发距往往较短（最大收发距3 m）,且工作频率较高（100 k、400 k和2 MHz）,因此其探测范围往往较小（最大探测深度5 m左右）（Li et al.,2005;Fang,2011;于蕾等,2021）.随着大斜度井和水平井在油气勘探开发中的广泛应用,不仅需要地质导向技术实现井眼轨迹优化,还需要精细了解井周数十米范围内的油气层空间分布情况,以便进行深部钻井的智能“巡航”,在更大范围内优化井眼轨迹,提高深层油气开发效率以降低成本（Kennedy et al.,2009;Omeragic et al.,2005）.因此,近十多年来,在常规随钻电磁波测井研究应用基础上,新型随钻超深前视电阻率测井技术也得到了快速发展（Rabinovich et al.,2011）.该项技术采用多频（1、2、4、8 kHz和16 kHz等）、长收发距（5～35 m）多分量线圈系组合测量（Dong et al.,2015;Wu et al.,2018）,并结合现代三维电磁正反演技术对井眼周围35 m径向范围内电导率空间分布进行精细成像,实现钻井优化、地质导向以及储层地质构造和水文地质条件的高分辨率精细描述.

在随钻超深前视电阻率测井技术研究、开发和应用过程中,需要进行仪器参数优化设计、考察复杂地层条件下探测特性并建立一套相应的资料处理和反演方法,特别需要指出的是,当前三维反演效率是满足不了实时处理需要的,所以在随钻资料处理中,可以根据地下电导率空间分布情况,预先设计井眼轨迹,并根据井眼轨迹和地层电导率分布,事先计算出一套正演模拟数据（理论合成响应）,然后将实测资料与理论合成响应进行对比,达到地质导向的目的,这些工作都需要随钻超深前视电阻率测井三维正演模拟技术.从理论上说,根据地层模型以及计算精度要求可以选择不同的数值模拟方法进行随钻超深前视电阻率测井响应的数值模拟.例如,对于分层介质,可以选用传输线法（Michalski and Mosig,1997;Yang et al.,2014）、传播矩阵法（康庄庄等,2020）、广义反射系数方法（Hong et al.,2014,2017）以及数值模式匹配法（Wang et al.,2008;林蔺等,2017;汪宏年等,2021）等算法,而对于复杂的三维地层模型,则可以采用三维有限元法（齐彦福等,2020）、三维有限差分法（Wang and Signorelli,2004;杨守文等,2009）、三维有限体积法（Haber et al.,2000;Wang et al.,2020;陈博等,2021）和积分方程法（陈桂波等,2009;汤井田等,2018）等.其中,有限体积法具有较好的守恒特性且易于实现,而引入耦合势能够有效的解决低感应数问题（Weiss and Newman,2003）.此外,在对源进行离散时,为了获得更高的精度,常常将电磁场分解为背景场与二次场,从而避免了直接对源离散（Irons et al.,2012;彭荣华等,2018）,但增加了额外的背景场计算成本,限制了其在三维数值方法中的应用,目前针对如何快速计算背景场的讨论较少.

随钻超深前视电阻率测井仪器的收发距变化范围大,本文将基于二次场耦合势三维有限体积法研究非均质各向异性地层中任意倾角的斜井中随钻超深前视电阻率测井响应数值模拟算法,以便提高正演模拟效率和整个计算区域内近场和远场的计算精度.为此,本文将通过Yee氏非均匀交错网格与三维有限体积法对二次场耦合势Helmholtz方程进行离散,并根据传输线算法形成层状地层中电磁场并矢Green函数库,同时结合二维Newton插值快速计算异常体内任意位置上的背景电场和散射电流,有效提高体分布散射电流源离散效率.在此基础上,采用并行直接求解器PARDISO快速稳定求解多源正演问题.最后,将算法应用于随钻超深前视电阻率测井仪器的正演模拟,验证了算法的有效性,并讨论了建库插值方法的计算效率.

1 基本原理

本节首先给出仪器结构和地层模型,并通过地层模型与电磁场的分解引入二次场与二次场耦合势Helmholtz方程,然后重点讨论体分布电流源计算与离散,给出背景场快速计算方法,以提高二次场方法的计算效率.

1.1 地层模型与电磁场分解

中国科学院地质与地球物理研究所目前正在自主研发随钻超深前视电阻率仪器,图1是仪器结构示意图,该仪器主要由一个三分量正交共位发射线圈Txyz（图1b）和三个不同收发距三分量正交共位接收线圈Rxyz（图1a）组成,并且发射器靠近钻头.为方便起见本文假定三个不同收发距L分别为5 m、15和35 m,而五个工作频率则假定为1、2、4、8 kHz和16 kHz （Dong et al.,2015;Wu et al.,2018）.

图2是倾斜井眼与三维非均质各向异性地层模型分解示意图.其中,井眼倾角为θ,而地层模型由起伏地层界面和几个局部异常体组成（图2a）,各层水平和垂直电导率分别用σH,n和σV,n,n=1,2,3表示.为便于描述倾斜或水平井眼情况下的正演过程,引入地层坐标系x′y′z′和井眼坐标系xyz（图2a）,其中,地层坐标系的z′轴垂直于层状背景地层界面d1和d2,且x′y′平面与背景地层界面平行.井眼坐标系的z轴与仪器钻进方向一致,y轴与地层坐标系中y′轴平行,井眼坐标系可由地层坐标系绕y′轴逆时针旋转θ角得到.

参照图2a中地层电导率空间分布,可以将其分解为层状背景模型（图2b）与三维局部异常体的组合（图2c）,对电磁场进行相应的分解,可以得到总电磁场方程（见附录A中（A1））、背景电磁场方程（A3）以及二次电磁场方程（A4）.其中背景电磁场采用传输线方法求解,二次电磁场则需要采用数值方法求解,并且为了克服低感应数问题引入耦合势（A5）,整理后得到二次场耦合势Helmholtz方程:

图1 随钻超深前视电阻率仪器结构示意图（a） 三分量阵列接收器;（b） 三分量发射器.Fig.1 Schematic diagram of the instrument structure of LWD ultra-deep look ahead multicomponent resistivity logging（a） Three-component array receivers;（b） Three-component transmitters.

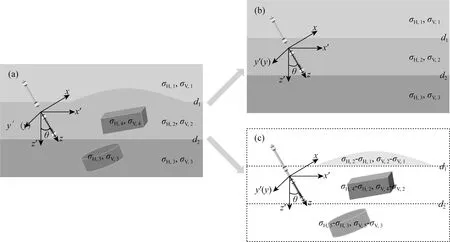
图2 复杂地层模型与分解示意图（a） 三维各向异性地层模型;（b） 水平层状背景地层模型;（c） 三维局部异常体模型.Fig.2 Schematic diagram of complex formation model and decomposition（a） 3D anisotropic formation model;（b） Horizontal layered background model;（c） 3D local abnormal bodies model.

=-iωμ0ΔJS,p（r,rs）

（1）

和

（2）

为求解方程（1）和（2）,选择足够大计算区域Ω并在其外边界∂Ω采用理想电导体边界条件（PEC）:

（3）

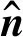
1.2 三维有限体积法

（4）

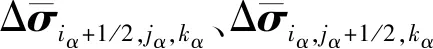
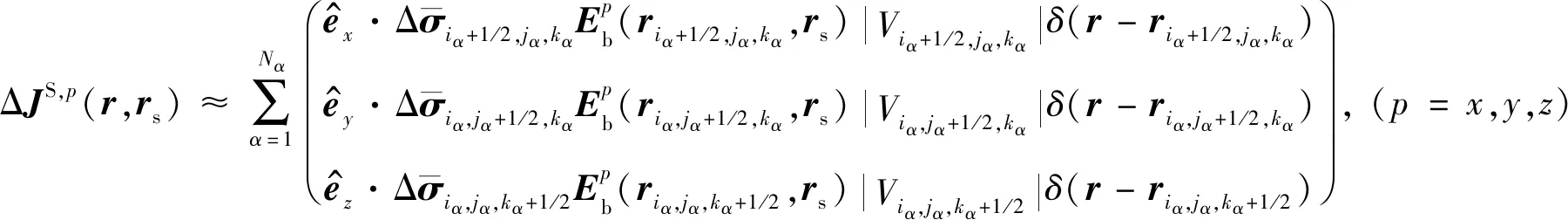
（5）

借助有限体积法对方程（5）分别在剖分单元Vi+1/2,j,k、Vi,j+1/2,k和Vi,j,k+1/2上进行体积平均,从而得到方程（1）的右端项离散结果:

（6a）

（6b）

（6c）

（7）

（8）

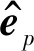
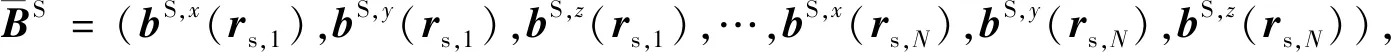
（9）

将方程（9）的二次场数值结果与背景场结合,可以计算出各个发射源产生的电磁场:

（10）

1.3 背景电磁场快速算法

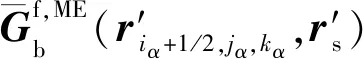
（12）

其中,基函数为

（13）

将式（12）的计算结果代入到附录（B6）式中就可以得到地层坐标系中背景电场并矢Green函数,结合如下转化公式:

2 数值结果

本节首先利用2.5D数值模式匹配算法（2.5D NMM）（Wang et al.,2008;林蔺等,2017）的数值结果对本文采用的二次场三维有限体积法（3D FV）进行对比验证,然后讨论背景电场计算过程,并将算法应用于随钻超深前视电阻率测井仪器的正演模拟.在数值结果中,将以发射源与接收器中心点作为记录点的位置,以便于不同收发距正演结果的对比,并将正演模拟结果转化为视电导率,以降低频率和收发距对正演结果的影响.视电导率各个分量为（张烨等,2012）:

（15）

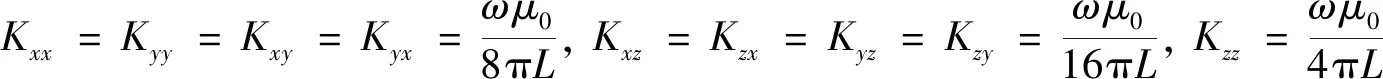
此外,在如下二次场耦合势三维有限体积法数值模拟中,网格节点数为（Nx,Ny,Nz）=（52,52,122）,并且x和y方向中间取30个步长为1 m的等间距网格,在中间网格外面再取10个步长为2 m等间距网格,最外围是12个渐变网格;而z方向的中间是40个步长为1 m等间距网格,在其外部则是40个步长为2 m等间距网格,然后是30个步长为3 m的等间距网格,最外围则是12个渐变网格,渐变网格根据Lebedev网格（Davydycheva et al.,2003）进行选取.文中所有数值结果都是在CPU型号为Intel（R） Xeon（R） Platinum 8269CY、主频2.50 GHz的工作站上计算得到的.

2.1 算法检验

为便于用2.5D NMM对二次场耦合势有限体积法加以检验,假定在水平和垂直电导率分别为0.2和0.1 S·m-1的均匀各向异性地层中包含着一个垂直柱状异常体（见图3）,该柱状异常体的水平和垂直电导率分别为0.125和0.05 S·m-1、其半径和高度分别为10和20 m,而井眼轨迹正好穿过圆柱的轴线.此外,还给出总场耦合势有限体积法的计算结果,以对比二次场方法与总场法的精度.

图4是仪器工作频率为1 kHz,收发距分别是5、15和35 m时三种不同正演算法计算得到的三个主分量的结果对比,其中,图4（a1）、（a2）和（a3）,图4（b1）、（b2）和（b3）以及图4（c1）、（c2）和（c3）分别对应收发距为5、15和35 m时的主分量视电导率σa,xx、σa,yy和σa,zz,黑色实线是NMM得到的结果,绿色星点是二次场耦合势有限体积法得到的结果,蓝色虚线是总场耦合势有限体积法得到的结果.二次场耦合势有限体积法与NMM得到的结果吻合很好,其相对误差（绝对值）均小于3%（见图4（a1′）、（a2′）和（a3′）,图4（b1′）、（b2′）和（b3′）以及图4（c1′）、（c2′）和（c3′）中绿色星点）,而总场耦合势有限体积法的误差明显更大（见图4（a1′）、（a2′）和（a3′）,图4（b1′）、（b2′）和（b3′）以及图4（c1′）、（c2′）和（c3′）中蓝色虚线）.此外,对比二次场法和总场法的相对误差曲线可以发现,二次场法的相对误差虽然都较小,但在异常体所在位置相对误差值会增大,产生这一现象的主要原因是这些深度点对应的发射源均位于柱状异常体内部,导致发射源所在单元中背景电场插值误差增大,从而影响了计算精度.而总场耦合势有限体积法相对误差却与二次场法相对误差变化特征完全不同,在异常体所在位置,总场法的相对误差明显降低,而在异常体外部的相对误差却明显增大,产生这一现象的主要原因是总场法中磁偶极子源的离散精度受网格大小影响非常明显,在异常体所在区域,因为网格尺寸较小（1 m）导致其离散误差下降,而在异常体外部采用了较大的网格尺寸（2 m）,引起离散误差明显增大.因此可以得出结论,在相同网格尺寸下,总场法的计算精度明显低于二次场方法,随钻超深前视电阻率测井的数值模拟需要考虑较大的计算区域,采用二次场方法有利于放宽对网格大小的要求.

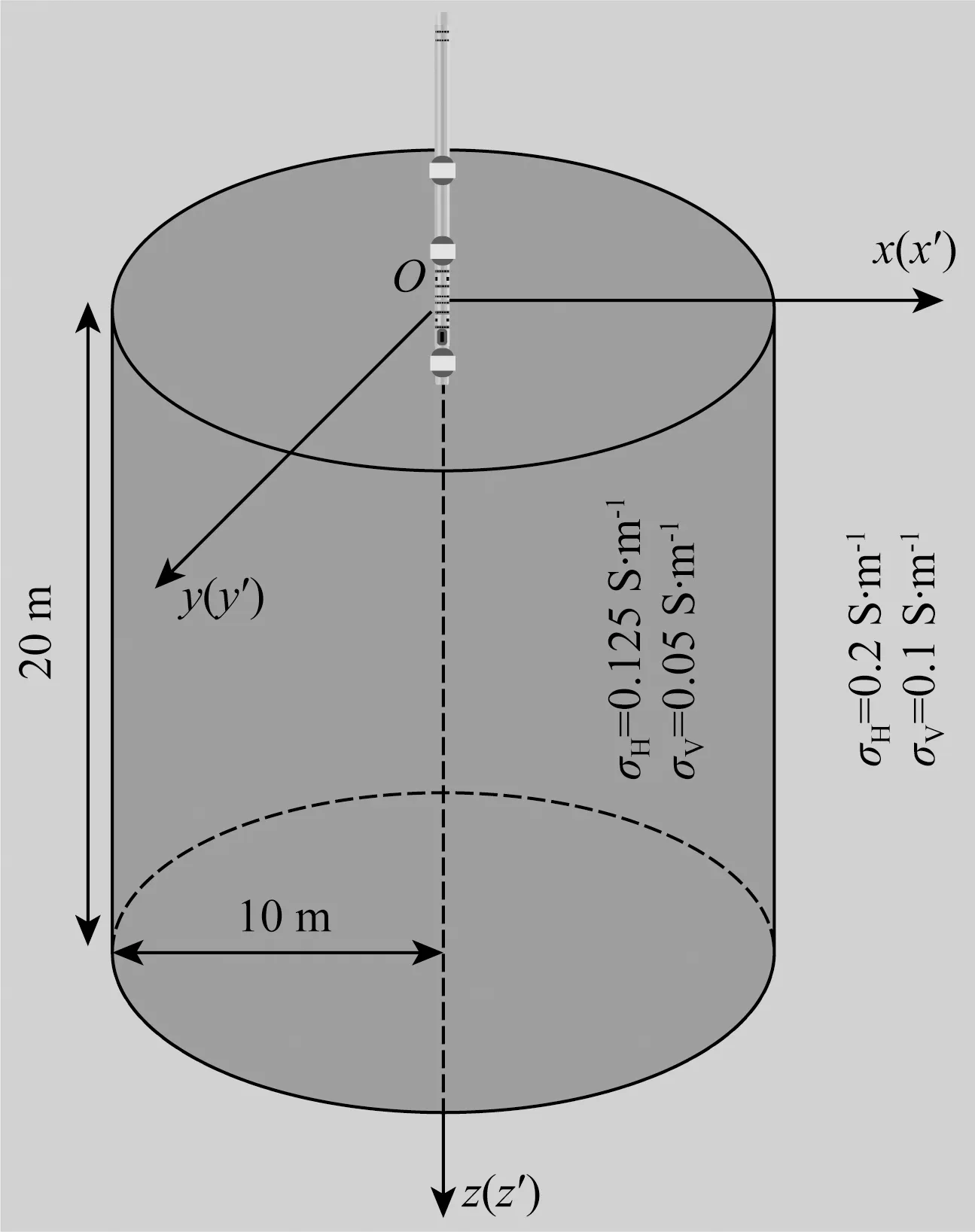
图3 圆柱异常体模型示意图Fig.3 Schematic diagram of cylinder model

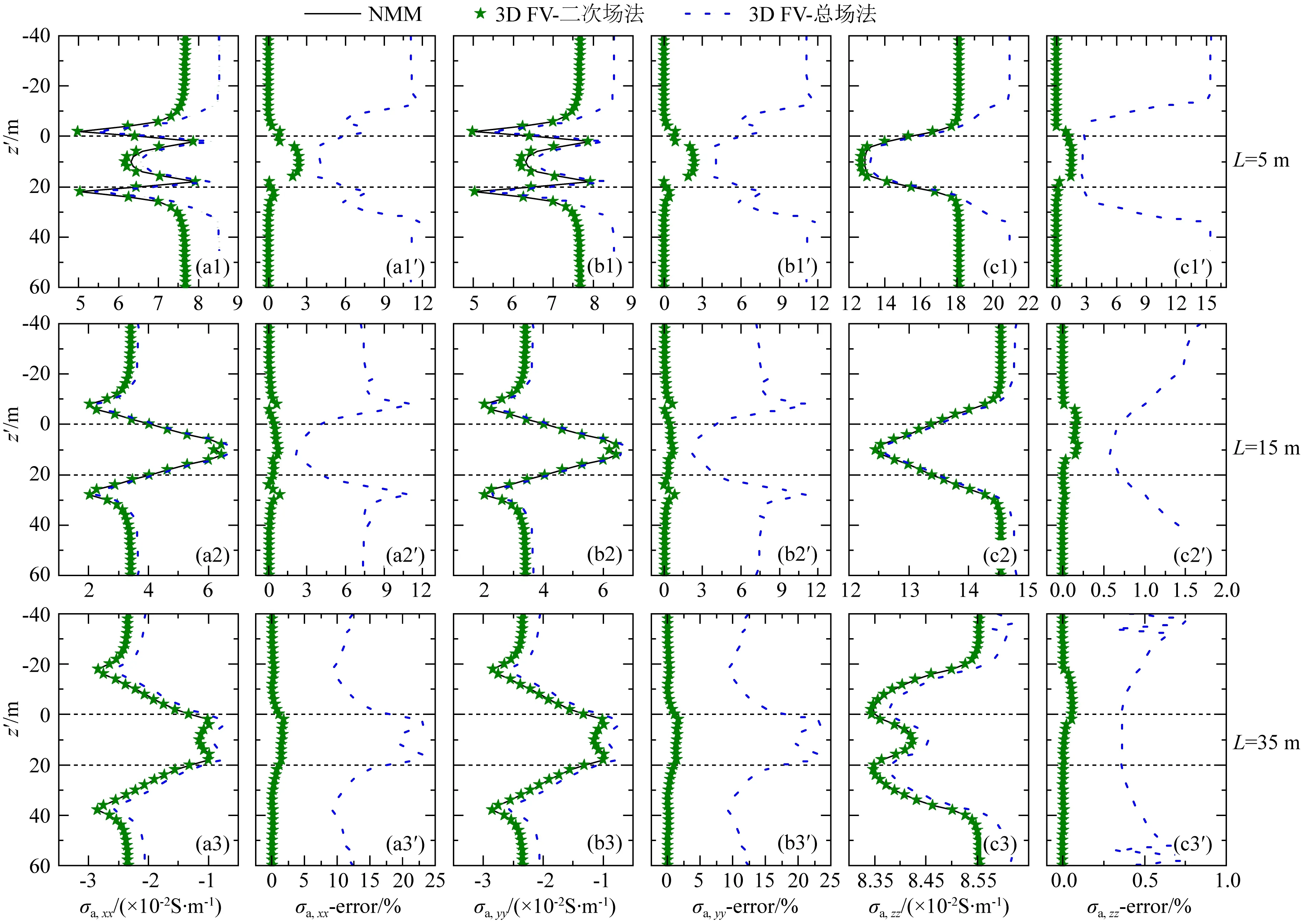
图4 圆柱模型中3D FV与NMM计算结果对比与误差分析Fig.4 The comparison of results obtained by 3D FV and NMM and error analysis in a cylinder model

2.2 长方体异常体模型

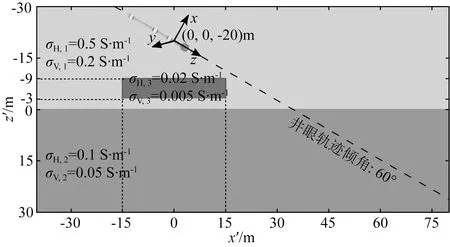
图5 长方体异常体模型示意图Fig.5 Schematic diagram of cuboid model

图5是双层各向异性层状背景地层中含有单个长方体异常体模型示意图.双层背景模型中,顶层水平和垂直电导率分别为0.5和0.2 S·m-1,底层水平和垂直电导率分别为0.1和0.05 S·m-1,异常体位于上部地层且水平和垂直电导率分别为0.02和0.005 S·m-1.在地层坐标系o′x′y′z′中,层界面位于z′=0 m处,异常体中心位置坐标为（0,0,6）m,在x′、y′和z′三个方向上的长度分别为30、30和6 m,且上下边界与背景地层界面平行.此外,假定倾斜井眼位于x′z′平面内且倾角为60°,井眼轨迹经过地层坐标系中的点（0,0,-20）m,并选择该点作为井眼坐标系oxyz的原点.整个井眼中共包含81个等间距测点,每一个测点都需要对三个不同位置发射源产生的背景电磁场进行计算,但不同测点对应的发射源位置可能会重复,所以在正演过程中实际只需要计算167个位于不同位置的三分量发射源产生的背景电磁场.

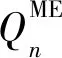
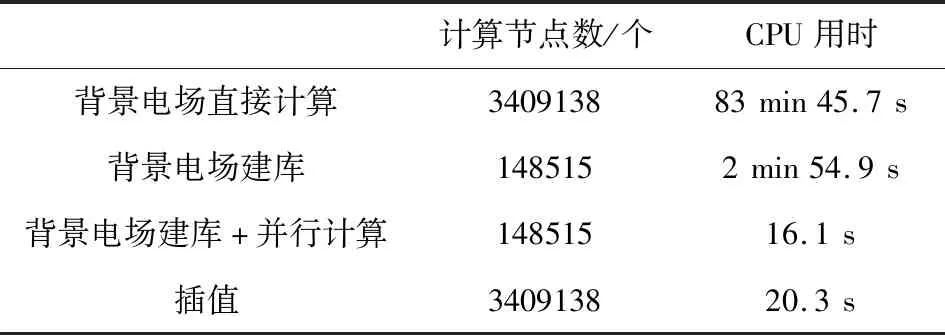
表1 计算背景电磁场CPU耗时对比Table 1 Comparison of CPU time for background electric field by different algorithms

为了对插值法计算精度进行考察,分别用插值法与传统TLM算法计算了倾斜井眼轨迹上背景视电导率（图6）,选定的收发距和工作频率分别为35 m和1 kHz.图6（a）、（b）、（c）、（d）和（e）分别对应五个背景视电导率分量σa,xx、σa,yy、σa,zz、σa,zx和σa,xz,其中黑色实线是TLM算法得到的结果,而绿色圆点是插值法得到的结果,两种方法得到的曲线吻合的非常好;图6f给出了对应的相对误差,各个分量的相对误差（绝对值）均不超过1%.

图7是模型5中三个不同收发距（L=5、15 m和35 m）和五个不同工作频率（1、2、4、8和16 kHz）情况下总视电导率和背景视电导率正演模拟结果,其中,图7（a1—a5）、图7（b1—b5）和图7（c1—c5）分别是收发距为5 m、15 m和35 m时五个不同频率下五个视电导率分量σa,xx、σa,yy、σa,zz、σa,zx和σa,xz的曲线,图中的实线表示总视电导率,虚线为背景视电导率.从图可以明显看出,收发距越长异常体对视电导率曲线的影响范围越大,说明收发距增加能够明显提高仪器的探测范围;此外,也可以看到工作频率变化对视电导率的影响,在源距不变的情况下，频率越低异常体对视电导率曲线的影响也越大,说明频率改变也能够有效调节仪器的探测范围.因此,通过多频率多源距的组合测量方式,能够获得仪器周围不同探测距离内的地层电导率分布信息,有利于进行井眼周围三维电导率反演成像.

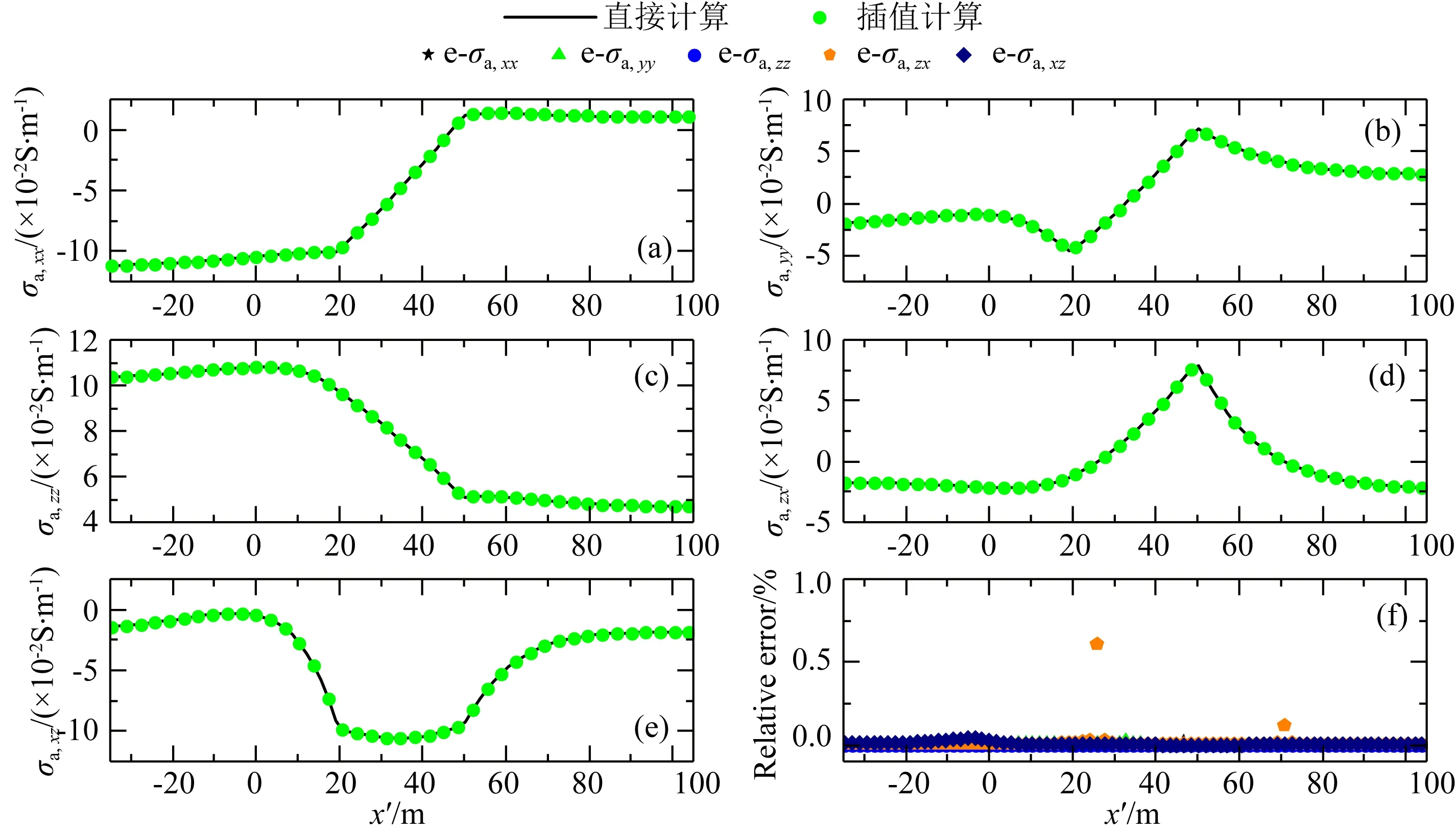
图6 插值法与传输线法得到的背景磁场响应对比Fig.6 The comparison of results obtained by interpolation method and conventional TLM

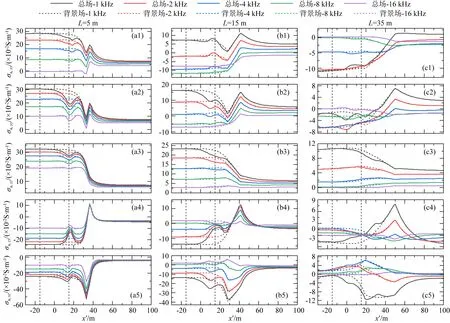
图7 长方体异常体模型中不同收发距与频率下仪器响应Fig.7 The instrument responses at different source distances and frequencies in cuboid model

2.3 二维起伏界面模型

图8 二维起伏界面模型示意图Fig.8 Schematic diagram of 2D undulating interface model

下面将考察二维起伏界面模型（图8）中的测井响应,模型中背景介质为双层模型,顶层的水平和垂直电导率分别为0.1和0.05 S·m-1,底层的水平和垂直电导率分别为0.01和0.005 S·m-1.在地层坐标系x′y′z′中,层界面位于z′=100 m处,起伏界面中心位置位于x′=0 m处,宽D取40 m,高H分别取4、8和12 m,以便考察起伏界面高度对仪器响应的影响,起伏界面在x′z′垂直平面上的截线方程为z′=H（x′+D/2）（x′-D/2）/（D/2）2+100.仪器位于底层地层中,井眼倾角为89°,并且井眼坐标系以地层坐标系中的点（0,0,105）m为原点.

首先给出起伏界面周围磁场的空间分布,为简洁起见,这里仅给出H为8 m时的结果.图9是单位发射源Mz在位于井眼坐标系的坐标原点时产生的磁场（虚部）在y′=0垂直截面上的分布情况.其中,图9（a1—a5）、图9（b1—b5）和图9（c1—c5）分别为背景磁场、二次磁场和总磁场在五个不同频率下的计算结果,结果显示,随着频率增加,发射源附近的背景磁场、二次磁场和总磁场的场值会逐渐变大,不同频率对应的磁场空间分布形态相似.在起伏界面周围,背景磁场方向沿逆时针方向（图9（a1—a5））,而二次磁场方向沿顺时针方向（图9（b1—b5））,因此起伏界面的存在使得总磁场的场值变小,从总磁场中可以明显看出起伏界面对磁场分布形态的影响（图9（c1—c5））.

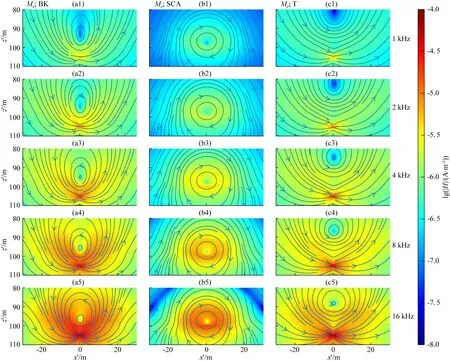
图9 Mz发射源激发的磁场在y′=0垂直平面的空间分布图Fig.9 Spatial distribution of magnetic field due to Mz source in y′=0 plane

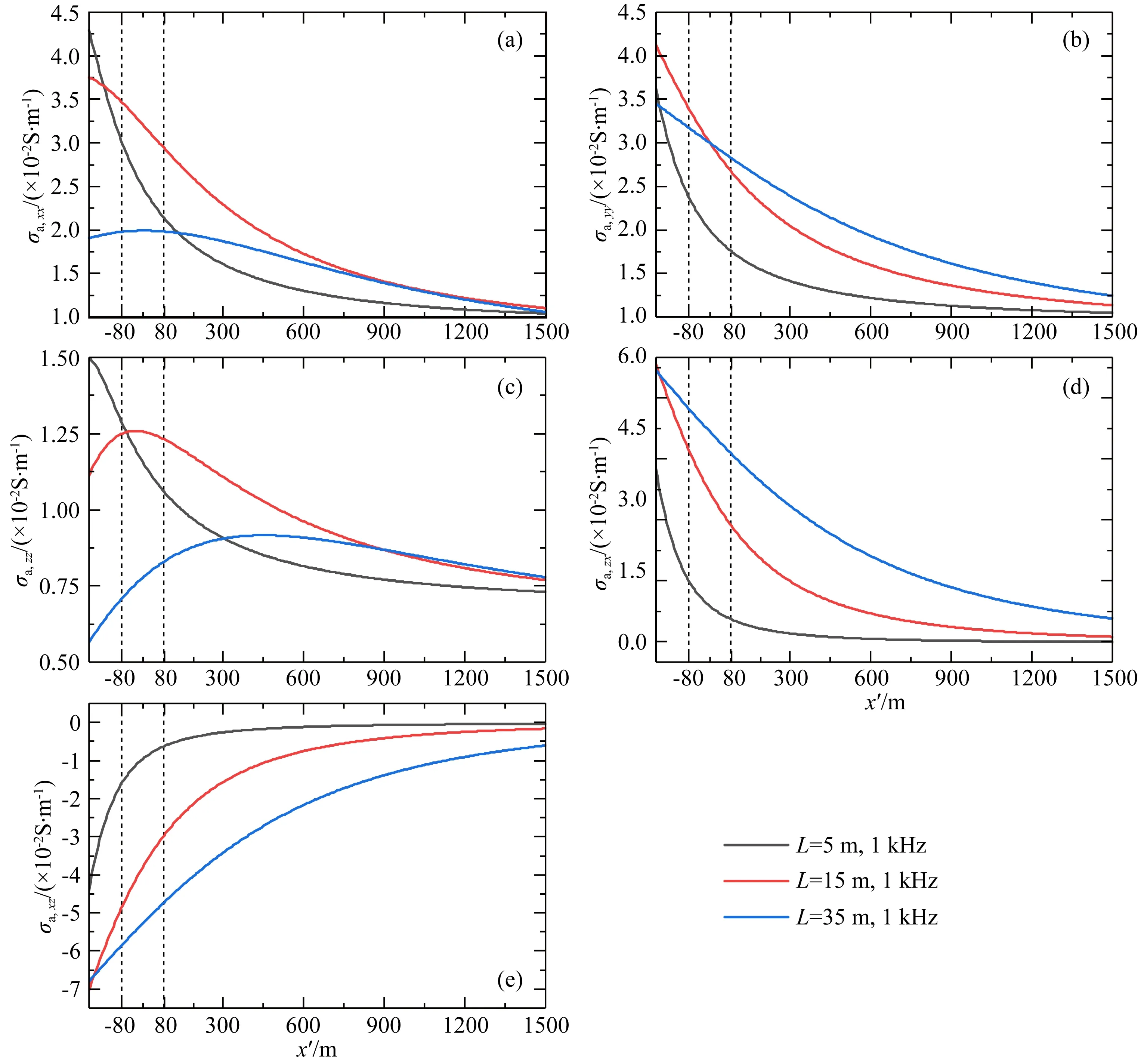
图10 89° 斜井中双层背景介质的仪器响应Fig.10 The instrument responses for a double-layer background medium in 89° deviated well

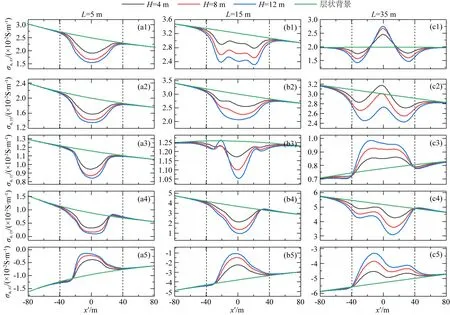
图11 89° 斜井中不同二维起伏界面高度下的仪器响应Fig.11 The instrument responses for different heights of 2D undulating interface in 89° deviated well

此外,在考察二维起伏界面对仪器响应的影响之前,先讨论图8模型中双层背景介质的测井响应,以便于了解在89°的大斜度井中不同源距的响应特征以及探边能力.为此,仪器工作频率选定为1 kHz,图10（a）、（b）、（c）、（d）和（e）给出了三个不同源距五个背景视电导率分量σa,xx、σa,yy、σa,zz、σa,zx和σa,xz的正演结果,整个背景响应沿水平方向x′的测量范围为-200～1500 m,即记录点从距离层边界1.5 m逐步增加到31.2 m.先观察并比较图10（a）、（b）和（c）中三个不同源距的主分量背景测井曲线,可以看出,短源距L=5 m三个主分量测井曲线在整个的计算范围内均是随变量x′单调变化的（也是层边界距离的单调函数）,这将十分有利于确定层边界位置,但当变量x′增加到大约600 m以后视电导率的变化变缓,说明其探边能力较弱;源距L=15 m两个主分量σa,xx和σa,yy与L=35 m主分量σa,yy在整个计算范围内也是单调变化的,并且视电导率在更远处才趋于平缓,说明其探边能力明显增强.此外,不难看出,L=15 m的主分量σa,zz和L=35 m的主分量σa,xx和σa,zz曲线不是单调变化,即在不同位置可能有相同的测量结果,显然不利于层界面反演.不过,与主分量不同的是,三个不同源距的交叉分量σa,zx和σa,xz均是随变量x′单调变化的,但其衰减较快,探测深度比主分量小.不同源距不同分量测井曲线的不同特征对于层界面反演是十分有利的,可以用不同曲线分别进行层界面反演,根据反演结果是否一致能够判断出层界是否起伏或层界面附近是否有异常体,因此采用多源距多分量组合测量是十分必要的,能够起到相互补充信息的目的.

在给出了层状背景响应的基础上,将进一步考察层界面起伏情况下的仪器响应,由于起伏地形仅有40 m的宽度,所以仅给出x′变化范围为-80～80 m（记录点与水平层界面距离为3.6～6.4 m）内的正演结果,在该范围外测井响应受起伏地形的影响已非常小,并且为简洁起见,这里仅给出工作频率为1 kHz的结果.图11（a1—a5）、图11 （b1—b5）和图10 （c1—c5）分别是源距为L=5、15和35 m时五个视电导率分量σa,xx、σa,yy、σa,zz、σa,zx和σa,xz的曲线,其中黑、红和蓝三条实线分别对应4、8和12 m三个不同高度的起伏界面,绿色实线则是层状背景介质中的背景视电导率曲线.起伏界面的存在直接增加了仪器与层界面的距离,起伏界面高度越大,各个分量的视电导率受底部地层的影响也越大,因此从图11中可以看出,三个不同源距测井响应与背景响应间的偏离程度随着起伏界面高度的增加而变大,然而,源距L=5 m的探测深度相对较小,起伏界面高度8 m和12 m间的测井响应已经相差较小（图11（a1—a5））,并且其各分量视电导率曲线形态与起伏界面形态匀是单峰曲线,从而有助判断界面形态.此外,由于源距L=15和35 m的探测范围较大,三个不同界面起伏高度H对应的五个视电导率分量间的差异十分明显（图11（b1—b5）和图10（c1—c5））,除了图11（b4）和（b5）对应的源距L=15 m交叉分量σa,zx和σa,xz以外,其他所有视电导率曲线均出现多峰现象,非常不利于层界面深度的反演.

3 结论

本文基于二次场耦合势三维有限体积法建立了一套随钻超深前视电阻率仪器数值模拟算法,有效保证了在大计算区域内电磁场的计算精度,与NMM的对比显示其相对误差小于3%,而在相同的剖分网格上,总场耦合势三维有限体积法的计算精度明显较差.此外,采用建库插值方法计算背景电场,在给出的算例中使背景电场的计算效率提高25倍,并能保证较好的计算精度,大大降低了在多发射源、大异常体情况下二次场方法的计算成本,提高了二次场方法在三维数值算法中的应用价值.

数值结果进一步证实了源距变大、工作频率变小能增加仪器的探测范围,探测范围变大使得在层状背景介质或含有异常体、起伏界面情况时,相应的测井响应变化特征会更为复杂,而短源距测量结果由于其探测范围较小,在仪器离界面距离较近时,其响应往往是层边界距离的单调变化函数,有利于用于层边界距离的反演;而不同源距交叉分量响应均具有随层边界距离的单调变化特征,也有利于层边界反演.

最后需要说明的是,在三维地层条件下,整个仪器的响应十分复杂,要想准确确定远离井眼的地层中电导率的空间分布,须研究开发出相应的三维反演算法.

附录A 电磁场分解

在井眼坐标系下,三维各向异性地层中多分量随钻超深前视电阻率测井响应实质上可以表示为求解如下Maxwell方程的问题（时谐因子取e-iω t）:

（A1）

其中,

（A2）

（A3）

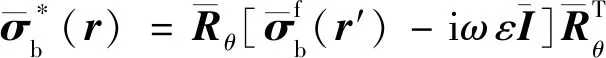
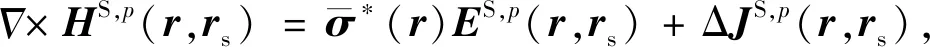
p=x,y,z

（A4）

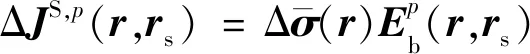
（A5）

附录B 水平层状TI介质中并矢Green函数计算

（B1）

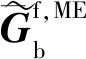
（B2）

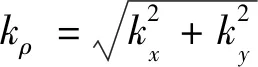
（B3）

（B4）

为对方程（B3）和（B4）进行二维Fourier逆变换确定频率-空间域中的并矢Green函数,定义如下形式Sommerfeld型积分:

（B5）

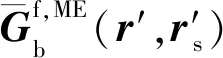
（B6）