模拟地震波传播的优化质量矩阵Legendre谱元法

刘少林，杨顶辉，孟雪莉，汪文帅，徐锡伟,李小凡

1 应急管理部国家自然灾害防治研究院，北京 100085 2 中国科学院地质与地球物理研究所，岩石圈演化国家重点实验室，北京 100029 3 清华大学数学科学系，北京 100084 4 宁夏大学数学统计学院，银川 750021 5 中国地质大学地球物理与空间信息学院，武汉 430074

0 引言

数值求解地震波运动方程不仅有利于认识复杂介质中地震波传播规律，同时是全波形地震成像的基础.迄今为止，研究者已开发出多种算法用于地震波运动方程直接求解，如有限差分法（Finite Difference Method，FDM）（Madariaga，1976；董良国等，2000；Zhang et al.，2012；Zhang and Yao，2013；刘少林等，2013；Liang et al.，2018），伪谱法（Pseudo-Spectral Method，PSM）（Wang and Takenaka，2011；杜启振等，2015；Li et al.，2021；Zou and Cheng，2018），有限元法（Finite Element Method，FEM）（Smith，1975；张怀等，2009）,谱元法（Spectral Element Method，SEM）（Komatitsch and Vilotte，1998；Komatitsch and Tromp，1999，2002；Yan et al.，2009；刘玉柱等，2020；刘少林等，2021；Shen et al.，2022）.FEM和SEM以其网格的灵活性以及能自动满足自由地表边界条件等优点而引起众多研究着的关注，并逐渐被应用于实际地震波的正演模拟与成像之中（Wei et al.，2018；Lei et al.，2020）.

FEM采用变分原理将地震波运动方程转化为积分形式（Marfurt，1984；Cohen，2002），并将求解域采用任意网格离散，最后在离散单元上对地震波方程数值离散并求解.不难发现FEM具有较好的网格灵活性，可适应任意复杂地质模型，同时可将FEM得到的地震波方程弱形式所包含的边界积分项设置为零，即可满足自由地表边界条件.虽然FEM具有以上显著优点，但也存在明显不足.其不足主要表现在三方面.首先，FEM求解地震波运动方程时计算量较大.FEM离散地震波运动方程以后得到的质量矩阵为非对角矩阵（Marfurt,1984），因此FEM需要求解大型线性方程组，计算量较大.虽然可通过质量集中算法将质量矩阵对角化（Liu et al.，2014b；刘少林等，2014），集中质量矩阵必然造成FEM精度损失（刘少林等，2014）.其次，FEM需要较大的计算机内存空间.地震波运动方程离散以后，FEM在每个单元上形成的单元刚度矩阵为稠密矩阵，存储稠密矩阵的非零元需要较大的计算机内存.虽然可采用FEM的存储改进算法，如核矩阵算法（Liu et al.，2014a）和单元矩阵重组算法（Meng and Fu，2017；苏波等，2019），能有效改进FEM存储量大的弊端，但这些算法往往会增加FEM的计算量.最后，FEM精度较低.在使用FEM模拟地震波场时，FEM在单元内对求解函数插值逼近时常采用低阶插值，虽然低阶插值计算量较小、计算速度快，但低阶插值面临着精度低、数值频散明显等缺点（Fichtner，2011；刘少林等，2014）.然而采用高阶插值不仅计算量增加而且Runge现象明显.FEM所具有的缺点，阻碍了该方法在地震波模拟领域的广泛应用（Bielak et al.，2005）.

SEM是一种极具潜力的地震波场数值模拟方法，该方法兼顾有限元法网格的灵活性与谱方法的高精度性.SEM最早在流体力学领域提出并得到发展和应用（Patera，1984），流体动力学数值模拟结果表明SEM具有精度高、快速收敛等优点.最早将SEM引入至地震学领域得益于Priolo和Seriani（1991）的研究.Priolo和Seriani（1991）利用SEM实现了二维声波的数值模拟，研究表明采用高阶SEM模拟声波时，SEM一个波长内的采样点数为7即可获得高精度模拟结果.随后，Seriani（Seriani et al.,1992;Seriani,1998）将SEM推广至弹性波的数值模拟.值得指出的是，早期的SEM在离散单元内采用Chebyshev多项式插值（Priolo and Seriani，1991）（记该类SEM为Chebyshev-SEM），但由于Chebyshev多项式带权正交（Wang et al.，2007），Chebyshev-SEM无法形成对角质量矩阵，在地震波场模拟时，在每一个时间步更新过程中都需要通过迭代方式求解大型线性方程组（Seriani，1997），因此计算量较大.虽然可采用矩阵张量积算子将稠密的单元刚度矩阵分解成若干个子矩阵，并将单元刚度矩阵与解向量的乘积分解为子矩阵与解向量的乘积，该矩阵分解算法能有效提升Chebyshev-SEM的并行计算效率（Seriani，1997），但并不能降低其计算量，在模拟三维地震波场时计算效率依然较低（Seriani，1998）.

SEM除了可采用Chebyshev正交多项式以外，还可以采用Legendre正交多项式（记该类SEM为Legendre-SEM）.Legendre-SEM相比于Chebyshev-SEM具有三方面的优点.首先，Legendre-SEM计算量较小.Legendre-SEM采用GLL点作为多项式的插值点，同时GLL点也为数值求积的积分点，由于积分点与插值点重合的特性，单元质量矩阵为对角矩阵（Komatitsch and Vilotte，1998），对角质量矩阵避免了迭代求解线性方程组，大幅减少了计算量.此外，插值点与数值积分点重合的特性可使得Legendre-SEM单元刚度矩阵具有稀疏的特点（刘少林等，2021），减少了矩阵与解向量乘积计算过程中的浮点运算次数.分析表明Legendre-SEM的浮点运算量与FDM相当（刘少林等，2021）.其次，Legendre-SEM的存储量较小.将Legendre-SEM的刚度矩阵采用矩阵张量积表示以后（刘少林等，2021），不难发现Legendre-SEM只用存储GLL点处雅克比矩阵及其行列式的值，无需存储稠密单元刚度矩阵，因此存储量较小.事实上，在相同网格点规模条件下Legendre-SEM采用任意非规则网格所需要的存储量与FDM相当（Komatitsch and Tromp，2002）.最后，Legendre-SEM单元内插值所使用的GLL点实际上是Fekete点（Fichtner，2011），Fekete点能保证多项式插值具有最优特性，插值多项式能对求解函数最优逼近.由于Legendre-SEM具有以上显著优点，该方法已逐渐成为一种重要的地震波模拟工具（周红，2018）.

少数研究者试图发展SEM的优化算法.例如Seriani和Oliveira（2007）将集中质量矩阵与一致质量矩阵优化加权组合用于降低Chebyshev-SEM的数值频散.然而该质量矩阵加权优化策略只在规则正方形单元网格中有效，而无法推广至一般非规则网格.由于Legendre-SEM在正交多项式和插值点选取上保证了其具有较高的数值精度，以至于文献中较少报道关于Legendre-SEM的优化格式.

值得指出的是，Legendre-SEM质量矩阵所包含的积分项中多项式的阶数不低于2N阶（其中N为单元插值多项式的阶数），而GLL数值求积的精度为2N-1阶，由于数值求积精度不足导致质量矩阵元素存在误差，质量矩阵所包含的误差在一定程度上会影响Legendre-SEM数值模拟精度.为了提升Legendre-SEM精度，需要对质量矩阵改进.借鉴有限差分法优化的思想（Zhang and Yao，2013；Wang et al.，2014；Liu,2020），构建关于质量矩阵的目标函数，将质量矩阵优化，减小质量矩阵积分项数值近似而代入的误差.通过数值频散分析和数值算例证实了本文提出的质量矩阵优化方法能提升Legendre-SEM地震波数值模拟精度.

1 理论与方法

为了论述方便记优化质量矩阵Legendre-SEM为优化谱元法（Optimal spectral-element method，OSEM），记常规的Legendre-SEM为传统谱元法（Conventional spectral-element method，CSEM）.

1.1 CSEM基本原理

为了本文论述的完整性，以2D弹性波运动方程为例简要介绍CSEM的基本原理，更详细的原理介绍请见Fichtner（2011）和刘少林等（2021）.2D非均匀各向同性介质中的弹性波运动方程可表示为

（1）

（2）

其中n为空间Ω边界处的单位法向量.根据自由地表边界条件和无穷远处自由边界条件，公式（2）中包含的边界积分项为0，因此地震波方程弱形式可简化为：

（3）

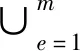
（4）

其中Ni（ξ1,ξ2）为关于单元控制点的形函数.通过求解方程（1-λ2）P′N（λ）=0（其中PN（λ）为N阶Legendre多项式）得到N+1个零点，通过这N+1个零点在每个四边形单元内可确定（N+1）2个插值点（等参坐标ξ1和ξ2每个坐标方向有N+1个插值点）.根据插值点以及插值点上u和v的离散值，在每个单元上的u和v可由以下公式近似：

（5）

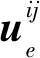
（6）

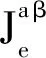
（7）

（8）

（9）

（10）

其中K1和K2的具体表述形式如下：

（11）

其中⊗为矩阵运算的张量积算子（Seriani，1997）.假设震源为点源，公式（1）中震源项可由矩张量表示：

（12）

其中M表示矩张量，xs表示震源位置，且震源位于标号为es的单元中，S（t）为震源时间函数.将（12）式以及公式（5）中ve的表示形式代入至（3）式等号右端第二项，关于震源项的离散形式有以下公式：

（13）

其中Fe具有以下形式：

（14）

其中Gij具有以下形式：

（15）

综合公式（6）、（9）和（13），公式（3）的离散形式为

（16）

由于测试向量v的任意性，公式（16）可进一步简化为

（17）

1.2 优化质量矩阵

从公式（7）和（A4）可知，质量矩阵所包含的积分项中被积多项式的阶数为2N+1阶（在2D情况下，单元的控制点数为4个），虽然由于GLL积分点和积分权的对称性，对于GLL数值求积公式能对任意奇数阶多项式精确求积（积分值为0），但对N+1点GLL数值求积公式只能对阶数不超过2N-2的偶数阶多项式精确求积，而无法准确估计2N阶多项式的积分值.由公式（7）可知，可通过调整数值积分权ωα从而使得质量矩阵的近似误差最小化.基于该考虑，构造以下目标函数:

（18）

其中变量c1和c2反映单元网格的变形程度，其具体形式见附录A.总体而言c1和c2的变化范围为[-0.2,0.2]（附录A）.为了保证质量守恒和能量守恒（Zhang and Yao,2013），需要对积分权系数增加以下限定条件：

（19）

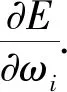
图1 利用CGM得到优化系数的流程图Fig.1 Flow chart for illustrating coefficient optimization using CGM

为了显示方便，表1只给出了优化权系数的左半部分.应该说明的是，当N=1时，在公式（19）的限定下，ωi无法进一步优化，因此表1不再列出N=1时的优化系数.为了对比优化积分权系数与常规GLL积分权系数的区别，表2给出了常规GLL积分权系数.从表1和表2对比可知，优化后的权系数与标准积分权相差较小，总体而言两者的相对差别在1/1000以内.两者的差别随着N的增加而变小，产生这种现象的原因在于SEM采用高阶多项式插值时标准的GLL数值求积得到的质量矩阵离散误差（公式（18））相比于低阶时要小，因此高阶插值时积分权系数无需过多调整即可使得公式（18）达到极小.

应该指出的是，第一，本文的质量矩阵优化策略不会增加或减少SEM的计算量.本文构造目标函数（18）式，通过优化选取数值积分权系数，从而减小质量矩阵离散误差，该过程并未改变数值积分点和插值点的位置，数值积分点和插值点仍保持一致，因此质量矩阵仍具有对称性（公式（7））.第二，公式（11）中K矩阵包含的积分权仍采用标准的GLL数值求积积分权.从K矩阵的推导过程可知（刘少林等，2021），由于空间梯度算子的作用（公式（1）和（2）），使得K矩阵所涉及的部分被积函数的阶数低于质量矩阵中被积函数的阶数，以至于标准的GLL数值求积在用于K矩阵的形成过程中引入误差相对较小，因此，本文不再讨论K矩阵的优化.第三，由于公式（18）不包含模型速度，因此优化系数不依赖于模型速度结构，当优化系数选定以后，OSEM可以用于不同模型的地震波场模拟，而无需再次进行系数优化.

表1 GLL数值求积的优化权系数Table 1 Optimized weights for GLL quadrature rule

表2 GLL数值求积的标准权系数Table 2 Standard weights for the GLL quadrature rule

2 理论分析

本节分析OSEM的数值频散特征和数值稳定性.根据De Basabe和Sen（2007）的讨论，可通过求解矩阵的一般特征值问题分析OSEM的数值频散与稳定性分析.本节只给出主要分析过程和结果，更加详细的原理推导过程请见文献De Basabe和Sen（2007）和刘少林等（2014）.

在理论分析中，空间网格由规则的正方形单元组成（Liu et al.,2017a），采用二阶中心差分近似公式（17）中的时间微分（Liu et al.，2017b）.假设地震波运动方程（公式（1））的解可写成如下简谐波的形式：

（20）

（21）

（22）

SEM的数值频散对地震波的传播角度和波速比并不敏感（De Basabe and Sen，2007），为了讨论方便，选取波数与x1坐标轴之间的夹角为30°和波速比r为1.6.为了减小时间离散误差对结果的干扰，选择较小的时间步长，使得q=0.005.OSEM和CSEM的数值频散如图2所示.图2显示，OSEM与CSEM的数值频散总体相似，都表现出SEM弱频散的特点.当N=2、3、5、7、8和9时，OSEM和CSEM的数值频散曲线几乎重合，为了对比需要，将频散曲线局部放大.从图2（a）、（b）、（d）、（f）、（g）和（h）中局部放大图可看出，OSEM计算的S波数值速度与物理速度之比相比于CSEM更靠近1，表明OSEM比CSEM具有更弱的数值频散.当N=4和6时（图2（c）和（e）），OSEM的数值频散明显小于CSEM.当N=4和6时，数值频散明显得到改善的可能原因是这些阶对应的优化系数相比与其他阶的优化系数更加接近全局最优系数.

从公式（22）不难看出，数值算法稳定性条件为

（23）

3 数值算例

本节通过三个数值算例说明OSEM在地震波场模拟时的高精度性.为了尽量减弱人工边界处的虚假反射，在边界截断处加入约10个波长（地震波主频对应的P波波长）厚度的PML吸收层（Komatitsch and Tromp，2003；Liu et al.，2014a；Xie et al.，2016；谢志南和章旭斌，2017；谢志南等，2019）.为了减小时间误差的干扰,数值模拟时采用远小于稳定限的时间步长.事实上，CSEM的高精度性已被大量文献所证实（Komatitsch and Vilotte，1998；De Basabe and Sen，2007；Liu et al.，2014b），为了定量讨论OSEM精度，本文选择10阶的CSEM作为参考.

3.1 均匀模型

选择如图3所示的各向同性均匀介质模型检验OSEM的计算精度.模型大小为2000 m×1000 m.模型介质的P波速度为2000 m·s-1，S波速度为1250 m·s-1，密度为2000 kg·m-3.一个垂直方向的集中力源位于（1000 m,50 m）处，其震源时间函数为主频为10 Hz的Ricker子波.两个接收器R1和R2分别位于（1500 m,0 m）和（1800 m,0 m）处.本次模拟空间网格单元尺寸为10 m，时间步长为0.05 ms.为了定量评估误差，定义接收点的最大误差max=‖Unum-Ur‖∞，其中U表示由归一化位移水平或垂直分量的时间序列组成的向量，上标num和r分别表示接收器处数值解与参考解.表3给出了OSEM计算得到的位移垂直分量最大误差（由于水平分量结果类似，因此不再讨论）.为了对比需要，表3也给出了CSEM的计算结果.

表3给出了当空间插值为2-9阶时OSEM和CSEM的最大误差.从表3可知OSEM和CSEM模拟均匀介质中地震波传播时均具有高精度的特点.当阶数为2时，OSEM和CSEM的相对误差均在2%以内.随着阶数的增加，OSEM和CSEM的相对误差均变小，当阶数为9阶时，相对误差减少至0.2%以内.OSEM和CSEM虽然都能较精确模拟均匀介质中弹性波，但OSEM的误差要小于CSEM.

3.2 分层模型

为检验OSEM在分层模型中的计算精度，设计了如图4所示的分层模型.模型的大小为4000 m×2000 m，模型内部存在两个分界面.上层界面由一倾斜面构成；下层界面由一起伏面构成.这两个分界面将模型分层三层，从上至下分别编号为A、B和C，每一层的参数如表4所示.采用四边形单元将模型离散，网格单元的平均尺寸为30 m.一个爆炸震源位于模型中心，其震源时间函数是主频为10 Hz的Ricker子波.两个接收器为R1和R2分别位于（3500 m,0 m）和（4500 m,0 m）处.空间采用8阶多项式插值.时间离散步长为0.01 ms.

图2 OSEM与CSEM数值频散曲线红色线是OSEM;黑色线是CSEM.（a）—（h）分别对应的空间插值阶数为2-9阶.（a）、（b）、（d）、（f）、（g）和（h）中OSEM和CSEM数值频散曲线几乎重合,为了对比需要,将频散曲线局部放大.Fig.2 The numerical dispersion curves of OSEM and CSEMThe red curves are calculated from OSEM;the black curves are computed from CSEM.Plots （a）—（h） are generated with spatial interpolations with second- to ninth-order,respectively.When N=2,3,5,7,8 and 9,the numerical dispersions of OSEM and CSEM are nearly consistent.For comparison purposes,portions of these dispersion curves in plots （a）,（b）,（d）,（f）,（g） and （h） are zoomed in.

表3 CSEM和OSEM模拟均匀介质中地震波传播的误差对比Table 3 A comparison of the maximum errors from CSEM and OSEM when modeling seismic waves in homogeneous media

图3 均匀介质模型用于检验OSEM的地震波数值模拟精度Fig.3 Homogeneous model is employed to investigate the accuracy of OSEM

OSEM模拟结果如图5和表5所示.从图5可看出，总体上看OSEM和CSEM得到的合成波形与参考波形几乎重合，两者在模拟层状介质中地震波传播时都具有高精度性.从图5可看到，在振幅较强的直达P波之后可看到明显的透射、反射震相.为了更清楚对比OSEM和CSEM的波形模拟精度，图6展示了波形误差.从图6可看出，总体上OSEM的波形误差（青色线）小于CSEM的波形误差（蓝色线）.为了定量对比OSEM和CSEM的计算精度，表5给出了OSEM和CSEM在R1和R2处合成波形水平分量和垂直分量的最大误差.从最大误差对比可看出，OSEM的精度要明显高于CSEM.

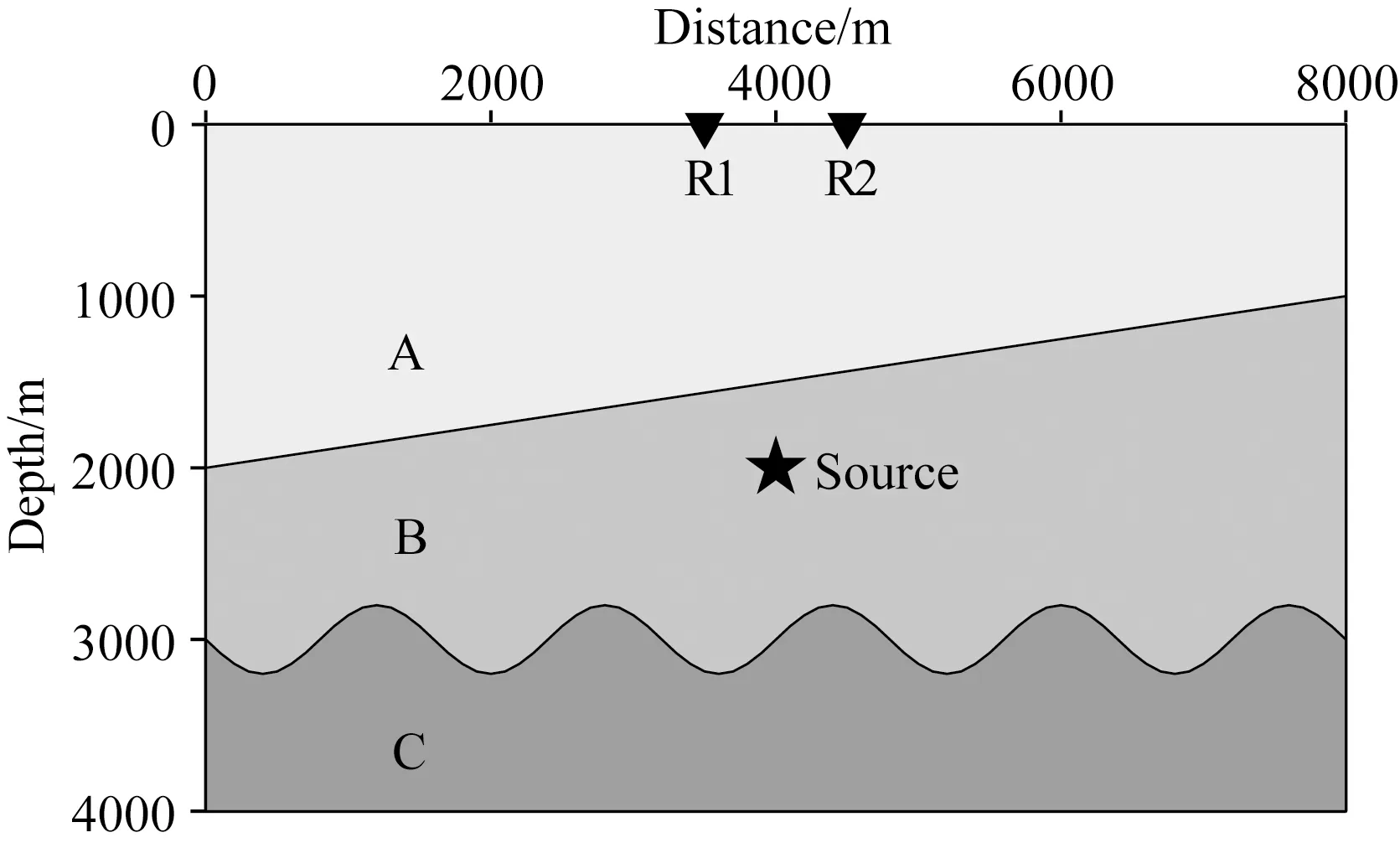
图4 分层介质模型两个分层界面将模型分成三层，从上往下分别记为A、B和C，每一层的介质参数如表4所示.图中五角星表示震源；三角形表示接收器.Fig.4 A model with three layersTwo interfaces divide the model into three layers,which is marked by A,B,and C,respectively.The parameters of each layer are shown in Table 4.The upper interface is an inclined line;the lower interface is an undulating line.

图5 合成波形与参考波形对比（a）与（c）分别为R1处波形的水平分量与垂直分量；（b）与（d）分别为R2处波形的水平分量与垂直分量.图中青线和蓝线分别由OSEM和CSEM计算得到；红线为参考波形.Fig.5 A comparison between the synthetic and reference waveformsPlots （a） and （c） respectively show the horizontal and vertical components of waveforms at R1.Plots （b） and （d） respectively show the horizontal and vertical components of waveforms at R2.Cyan lines are generated by OSEM;blue lines are computed by CSEM.Red lines represent reference waveforms.

表4 分层模型介质参数Table 4 Media parameters of the layered model in Fig.3

图6 OSEM和CSEM得到的合成波形误差对比（a）和（b）为R1处的合成波形误差；（c）和（d）为R2处的合成波形误差.（a）和（c）为水平分量误差；（c）和（d）为垂直方向误差.Fig.6 A comparison between errors of synthetic waveformsPlots （a） and （b） are at the receiver R1;plots （c） and （d） are at the receiver R2;Plots （a） and （c） are for the horizontal components;plots （b） and （d） are for the vertical components.Cyan lines are generated by OSEM;blue lines are computed by CSEM.

表5 层状介质中OSEM与CSEM模拟精度对比Table 5 A comparison of the accuracy of OSEM and CSEM in layered model

3.3 起伏模型

设计如图7的所示模型用于检验OSEM在起伏地表模型中地震波模拟精度.模型水平方向延伸10000 m，垂直向下延伸至地下5000 m处.如图7所示，模型除了地表具有强烈起伏外，模型内部还存在分层界面.模型上下两层的P波、S波以及密度参数显示在图7中.一个爆炸源位于（5000 m,1000 m）处，其震源时间函数是主频为15 Hz的Ricker子波.5个接收器（图7中黑色三角形）从上往下分别编号为1-5.采用四边形单元离散模型，四边形单元的平均尺寸为30 m，该网格尺寸能保证最短波长内平均单元采样数约为2.OSEM空间插值多项式的阶数为4.时间步长为0.01 ms.模拟结果如图8所示.

图7 地表起伏模型模型地表处起伏强烈，此外模型内部具有一倾斜界面.模型介质参数在图中给出.五角星代表震源；地表处的三角形表示接收器.Fig.7 A model with rugged topographyBeside the topography,an incline interface is inside the model.The parameters of the model are presented in the plot.The star at （5000 m,1000 m） denotes the source;the triangles represent the receivers.

为了对比，图8也展示了CSEM波形模拟结果.从模拟结果可看出，OSEM和CSEM均能准确模拟地表强烈起伏模型中地震波传播.从合成地震记录中可看到除了振幅较强的直达波以外，还在直达波之后发现明显的反射波，以及可看到来自地表起伏界面的多次反射波.从图8难以直接看出OSEM和CSEM两者精度差别.为了定量对比，计算OSEM和CSEM的水平和垂直分量最大误差，OSEM的水平和垂直分量最大误差分别为3.881776×10-2和4.219775×10-2，CSEM的水平和垂直分量最大误差分别为4.048275×10-2和4.297425×10-2.由此对比可以知，OSEM的精度要高于CSEM.

4 讨论与结论

本文提出了一种质量矩阵优化策略用于减小SEM质量矩阵中包含的误差.本文核心思想在于构造数值积分与真实积分的最小二乘目标函数，通过优化方法选取数值积分权用于减少质量矩阵误差.通过理论分析和实际算例证实了该优化策略能有效提升SEM地震波模拟的计算精度.本文对SEM的优化并不增加计算量，而只用修改SEM质量矩阵中所包含的积分权便可获得精度提升.应该指出的是，随着插值阶数的提高，OSEM的精度提升越来越小.在实际地震波场模拟时，为了在计算效率与精度之间达到平衡，往往空间插值阶数不超过5阶.因此，当采用OSEM用于实际地震波场模拟时，建议空间采用2-5阶插值.

应该指出的是，本文提出的优化策略并未破坏SEM正交多项式的正交性，因此SEM的高精度性以及指数收敛性仍得到了保持.实事上，传统的SEM通过选取正交多项式和Fekete点用于多项式插值和逼近待求解函数，使其具有较高的数值精度.本文的贡献在于，可通过优化策略将SEM的精度进一步提升.本文在优化目标函数的过程中，只采用CGM用于系数的优化，以至于只能得到局部最优的优化系数.如果采用全局优化方法（如模拟退化方法、蒙特卡洛方法），有可能获得全局最优的优化系数，从而有望进一步提升SEM精度.本文提出的质量矩阵优化策略可方便推广至三维SEM，通过构造三维情况下关于质量矩阵的目标函数（与公式（18）类似），可得到适用于三维SEM的优化权系数和优化质量矩阵.

图8 接收器记录的波形对比（a）和（b）分别为水平方向位移和垂直方向位移；青色线、蓝色线和红色线分别为OSEM、CSEM和参考解得到的合成波形.Fig.8 Comparison of synthetic waveformsPlots （a） and （b） show horizontal and vertical components of displacements,respectively;Cyan,blue and red lines are generated by OSEM,CSEM and reference solution,respectively.

致谢感谢两名匿名审稿专家对本文提出的建设性意见.感谢与中国科学院地质与地球物理研究所刘有山副研究员的讨论.本文的计算模拟在中国地质大学（武汉）地球物理与空间信息学院的TS10000服务器上完成.

附录A

（A1）

由公式（A1），雅克比矩阵可表示为

（A2）

其中a1-a4和b1-b2的表达形式如下：

（A3）

由公式（A2）可知雅克比矩阵行列式的值可表示为

附图A1 四种典型四边形单元用于讨论c1和c2（a）—（d）对应的（c1,c2）值分别为（0,0）、（0.2,0.2）、（-0.2,-0.2）和（-0.2,0.2）.Fig.A1 Four typical quadrilateral elements to discuss the values of c1 and c2The elements in plots （a）—（d） are with （c1,c2） of （0,0）,（0.2,0.2）,（-0.2,-0.2） and （-0.2,0.2）,respectively.