地震辐射能量测定方法研究及其在汶川8.0级地震中的应用

孔韩东,刘瑞丰,边银菊,李赞,王子博,胡岩松

中国地震局地球物理研究所，北京 100081

0 引言

地震时以地震波的形式传播的能量称为地震辐射能量，它是地震释放总能量的一部分，正是这部分能量对地震波传播经过的区域造成了破坏.地震辐射能量是衡量地震大小的基本参数，可以反映地震破裂的动态过程，断层在不同的错动时间历程所激发的地震波的波形和幅值可能有明显的区别，即辐射的地震波的频谱显著不同，因而对建筑的影响和破坏也不同，研究地震辐射能量的大小一直是地震学的重要问题.

地震辐射能量的测定始于1915年Galizin对1911年帕米尔地震的地震辐射能量的研究.地震辐射能量的测定方法大致可以归结为两种：一种是利用地震矩和应力降，属于静态测量法；另一种是直接通过地震波形计算，属于动态测量法.动态测量法又可以分为两种：一种是通过远场位移波形计算；另一种是通过断层面上应力、位错进行计算.其中，用远场位移波形计算可以直接对台站波形记录中的体波进行积分或对震源时间函数进行积分.Kanamori（1977）曾尝试基于静态震源参数（如地震矩M0和断层面积S）计算地震辐射能量.近年来随着数字地震学的发展，已经可以使用数字地震观测资料直接测定地震辐射能量.Boatwright（1980）和Kanamori等（1993）在时间域求速度记录平方的积分得到地震辐射能量.Shoja-Taheri和Anderson（1988）在频率域求速度记录平方的积分得到地震辐射能量.Boatwright和Choy（1986）计算地震辐射能量时，使用经验路径法校正远场P波速度记录，使测定结果更加准确.Newman和Okal（1998）简化了他们的计算过程，使之适用于海啸地震的实时预警.Convers和Newman（2011）用以上算法，测定了1990年以来全球MW≥6.0地震的地震辐射能量和能量震级，并在美国地震学研究联合会（IRIS）的地震能量查询网站（http:∥www.iris.edu/spud/eqenergy）公布.Vassiliou和Kanamori（1982）基于Haskell（1964）的工作给出了利用震源时间函数计算地震辐射能量的公式，后被许多学者采用（Kanamori et al.,1993;Singh and Ordaz,1994;Boatwright et al.,2002;Boatwright and Seekins,2011）.Mayeda和Walter（1996）、Mayeda等（2003）和Morasca等（2005）利用S波直达波后的散射尾波计算地震辐射能量.Pulido和Irikura（2000）在时间域求震源时间函数的微商，再积分计算地震辐射能量.Izutani和Kanamori（2001）在频率域求震源谱的积分，计算地震辐射能量.Ide（2002），Favreau和Archuleta（2003）、Mori等（2003）通过地震的动态破裂模型（dynamic rupture model）计算地震辐射能量.Di Giacomo（2010）和李赞等（2019）通过理论格林函数法校正路径效应，使用远场P波计算地震辐射能量.针对计算地震辐射能量时存在的频带限制的问题，前人也做了很多研究（Ide and Beroza,2001;Venkataraman et al.,2002;Singh et al.,2004,华卫等,2012）.

目前，国际上仅有美国地质调查局（United States Geological Survey,USGS）国家地震信息中心（National Earthquake Information Center,NEIC）在地震发生后会常规产出地震辐射能量和能量震级.德国地球科学研究中心（GFZ）曾采用Di Giacomo（2010）提出的方法测定地震辐射能量和能量震级，现在已经不再发布.在国内，一些学者也做过相关工作（如刘杰等,2003;兰从欣等,2005；华卫等,2012；郑建常等,2016等），但都没有形成系统的方法和成熟的软件.国内的地震台网日常产出中也没有地震辐射能量和能量震级这两个基本地震参数.如果能够对地震辐射能量的测定方法进行系统研究并开发出一套自己的地震辐射能量和能量震级测定软件，使地震辐射能量和能量震级变为可常规产出的地震参数，对于我国地震行业的发展将具有重要意义.基于这个目的，我们从地震点源模型出发，对地震辐射能量测定的理论公式进行了推导，独立开发了一套可以快速测定地震辐射能量和能量震级的软件系统，并以2008年汶川8.0级地震为例进行软件展示.

1 地震辐射能量计算方法

从应力做功的角度考虑，可以沿包围震源的曲面S对震源在整个地震发生时间内发射的弹性地震波的能量通量积分计算地震辐射能量（Kostrov,1974）：

（1）

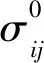
（2）

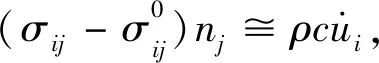
（3）

基于矩张量表示的点源地震模型产生的体波远场位移表达式分别为（陈运泰和顾浩鼎,1990）：

（4）

（5）

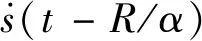
将公式（4）（5）代入公式（3），对立体角和时间积分，可以得到远场地震辐射能量的计算公式：

（6）

（7）

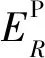
（8）

（9）

地震波携带的总能量在频率域中可以表示为

（10）

将ω=2πf代入公式（10）可得：

（11）

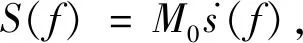
（12）

式中只有远场震源时间函数谱S（f）一个未知量.因此，求地震辐射能量的问题就转化为了求远场震源时间函数谱的问题.

震源时间函数描述震源的时间历史，它可以是地震断层的滑动量或滑动率的时间历史，也可以是地震震源地震矩或地震矩率的时间历史.如果用地震矩描述震源，不考虑体力和应力的间断性，则在一个分界面Σ两侧的位移间断[uj（ξ,τ）]所引起的弹性位移具有如下所示的简单表示式（陈运泰和顾浩鼎,1990）：

（13）

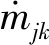
当断层的尺度和所考虑的波长相比很小的时候，可以将地震震源看作是一个点源，此时，公式（13）有更简单的形式（Lay and Wallace,1995）：

（14）

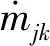
（15）

代入公式（12），可得：

（16）

由公式（14）可知，s实际观测波形在格林函数解卷积后可以得到震源时间函数，同时可以消除路径效应的影响.本文通过计算理论格林函数并合成理论地震图，然后提取振幅谱衰减函数（spectral amplitude decay functions）校正地震波在传播过程中与频率相关的能量损失（Duda and Yanovskaya,1993）.与经验方法相比，使用理论格林函数法消除路径效应有如下优势：理论格林函数使用数值模拟的方法，从一个已知点源出发，可以解释不同频率的传播效应.为适用于全球浅源地震，选用AK135一维速度模型（Kennett et al.,1995;Montagner and Kennett,1996）.图1给出了震源深度h=12.8 km的远场理论地震图.我们使用反演出的震源机制解对理论地震图进行震源校正，使合成结果更接近真实情况，避免了不准确的震源机制对地震辐射能量测定结果的影响.然后，按以下方法从时间序列中提取振幅谱衰减函数：计算每个震中距上的P波序列的傅里叶谱，然后提取指定频率的振幅谱衰减.图2 以周期T=16 s为例，展示了振幅谱衰减函数.根据不同周期（频率）的振幅谱衰减函数，可以对实际波形进行衰减校正.

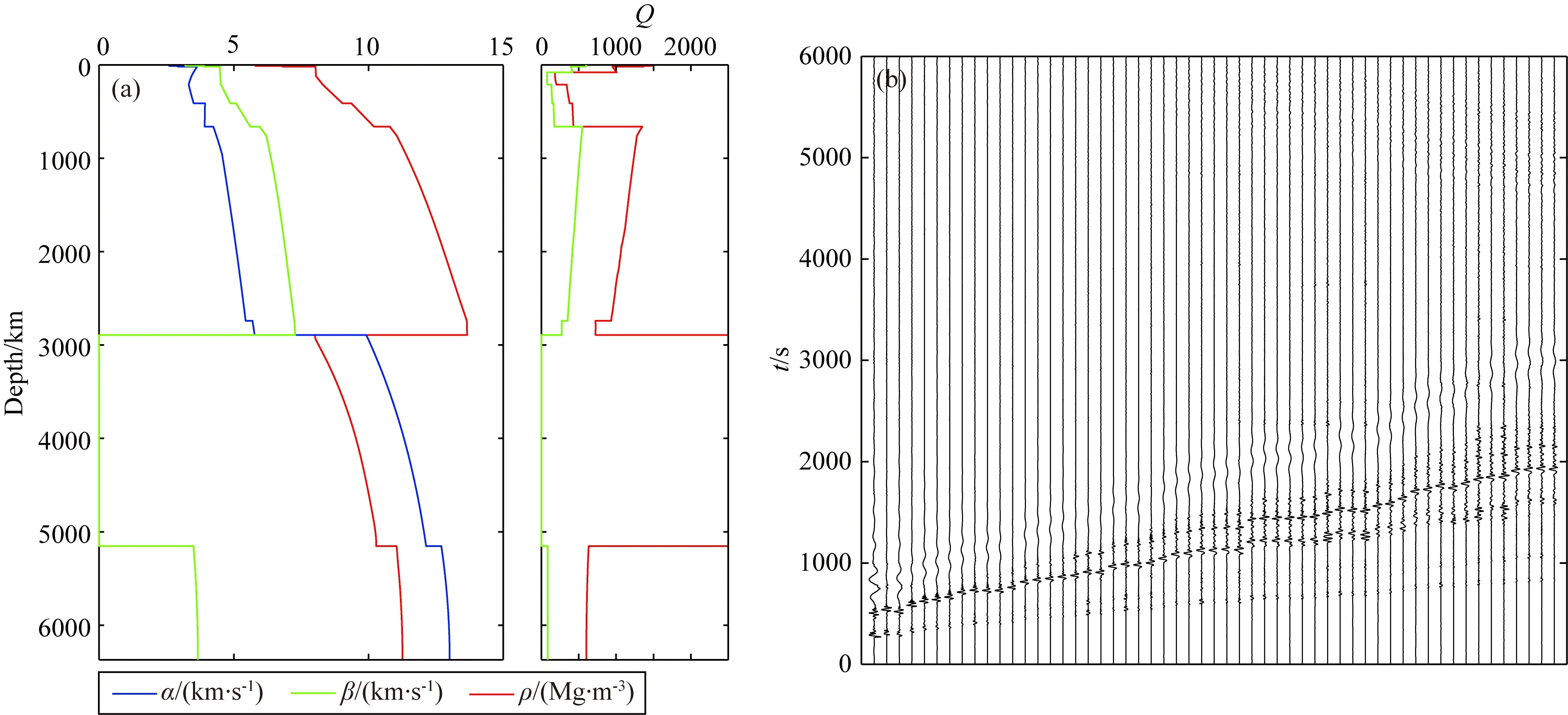
图1 （a） AK135一维地球参考模型及（b） 远场P波理论地震图（h=12.8 km）（横轴按震中距由小到大排序）Fig.1 （a） The one-dimension reference Earth model AK135;（b）Theoretical seismogram of teleseismic P-wave （h=12.8 km）,the x-axis is sorted by epicenter distance

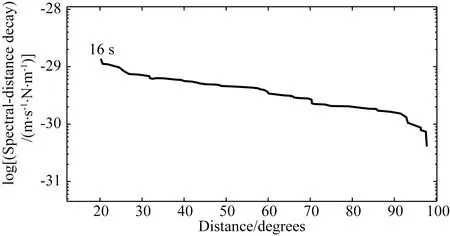
图2 振幅谱衰减函数（T=16 s）Fig.2 Spectral amplitude decay functions for period T=16 s

由公式（16）可知，计算地震辐射能量时，理论上应该对震源谱覆盖的整个频段积分.但在实际应用中，由于存在各种限制无法实现.因此，只能尽可能地选取合适的频段.此时，公式（16）变为

（17）

其中，f1和f2分别为积分频段的上限和下限.本文使用的积分频段为f2=12.4 mHz至f1=1 Hz.

为实用起见，根据震源深度不同将地震分为两组.根据AK135模型一维平均球面结构中的数据确定公式（17）中α、β和ρ各自的取值，即当震源深度h<18 km 时，α、β和ρ分别取6.8 km·s-1、3.9 km·s-1、2.92 g·cm-3；当震源深度18 km≤h≤70 km时，α、β和ρ分别取8.0355 km·s-1、4.4839km·s-1、3.641 g·cm-3.选择18 km作为分界面是因为其上下深度的变化不会在Me的估算中引入很大的差异（Di Giacomo et al.,2010）.

根据远场地震辐射能量的计算公式，选择震中距20°～98°的垂直向P波资料测定地震辐射能量.因为在传播过程中地震波受沿路径衰减的影响非常明显，P波携带的地震辐射能量虽然比例较小，但受衰减的影响比S波要小的多，因此常被用于地震辐射能量的测定（Boatwright and Choy,1986;Choy and Boatwright,1995;Tajima and Fumiko,2007;Allmann and Shearer,2009;Di Giacomo et al,2008,2010;Di Giacomo,2010;李赞等,2019;王子博等,2021）；而且P波传播速度更快，可以第一时间被地震台接收.

2 地震辐射能量测定软件的开发

以上述理论为基础，我们开展了地震辐射能量测定软件的自主研发工作.软件主要包括数据处理、快速震源机制反演、时窗计算、理论格林函数计算和地震辐射能量计算五个主要模块，软件各模块的主要功能及大致运行流程如图3所示.

（1）数据处理模块

该模块的主要功能是将地震仪器接收到的波形数据去除仪器响应后还原成真实的速度记录.模块采用时间域剔除仪器响应的技术（Kanamori et al.,1999;Kanamori and Rivera,2008），从观测数据中去除仪器响应，避免了可能由于奇异值造成的频率域结果不稳定和可能由于面波限幅对体波的影响.

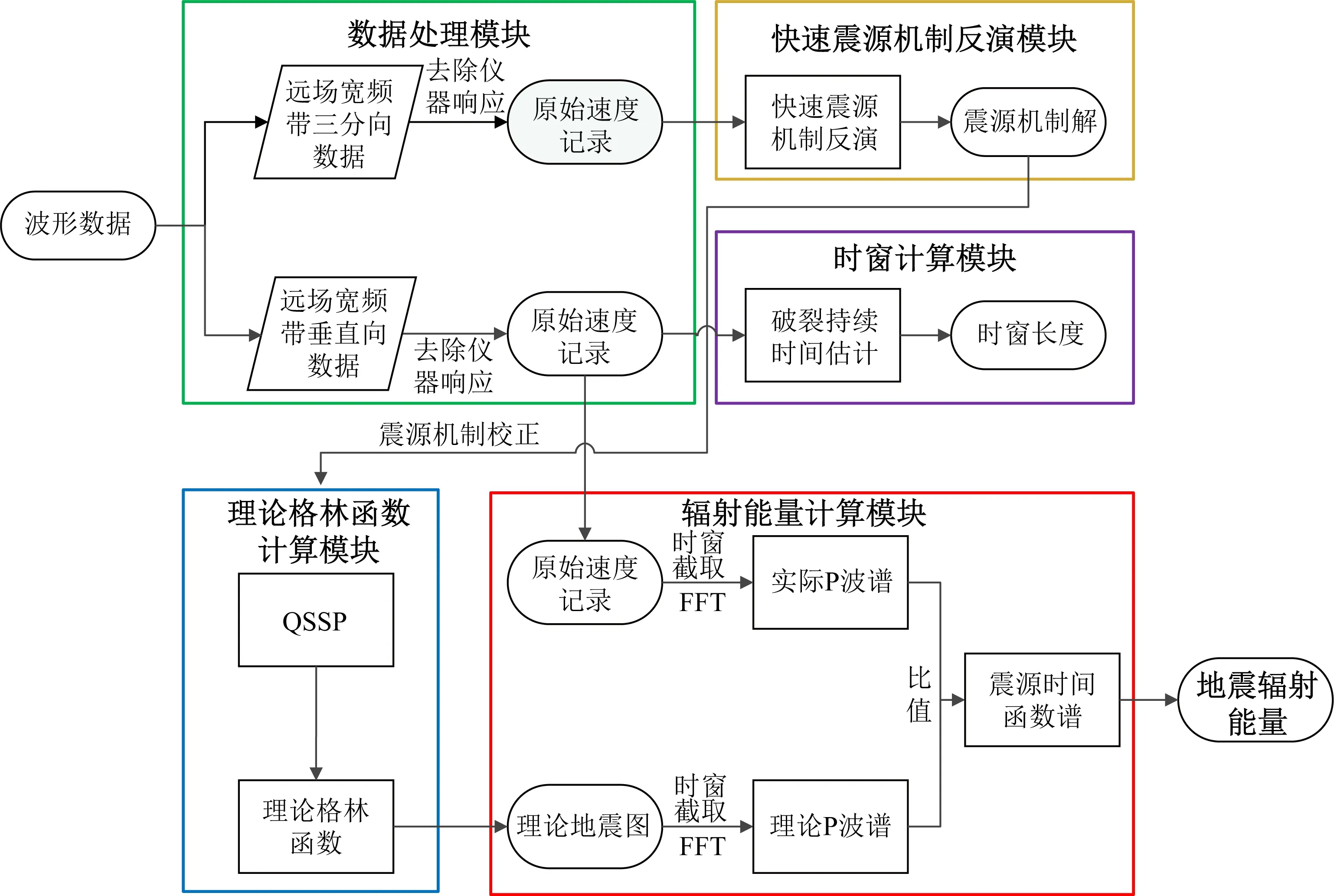
图3 地震辐射能量测定程序的主要模块及流程Fig.3 The major modules and flowchart of the seismic radiated energy determining software

（2）快速震源机制反演模块

该模块的主要功能是快速反演震源机制，得到的震源机制解用于合成理论地震图.计算地震辐射能量时加入震源机制校正，可以提高测定结果的可靠性和稳定性.震源参数中的地震矩还可以用于计算矩震级、能矩比、慢度系数和等效震级差等新的地震参数，丰富软件产出，为地震灾害评估机构提供更多参考.

（3）时窗计算模块

该模块的主要功能是计算时窗长度.测定地震辐射能量时需要截取P波，我们将截取P波的时间窗口的长度称为时窗长度.

通过粗略估计地震的破裂持续时间可以确定时窗长度.因此，我们参考了Bormann和Saul（2008,2009）估计地震破裂持续时间的工作.确定时窗长度的具体流程为：计算经1～3 Hz滤波的各个台站的P波速度记录的包络，将所有包络以P波初至为参考对齐并求平均包络，将包络幅值低于最大值40%时的时间点设为时窗长度.这一方法避免了时窗饱和效应对震级测定的影响（Bormann et al.,2007），它类似于Hara（2007）和Lomax等（2007）的方法，是对实际破裂持续时间的一种粗略的估计（一般大于实际破裂时间）.通过求多个台站波形包络线的平均值，可以对整个P波列的持续时间进行稳定估计，保证与地震辐射能量测定相关的信号包含在时窗内.图4为本文使用汶川地震数据计算时窗长度过程的示例.

（4）理论格林函数计算模块

该模块的主要功能是计算理论格林函数，用于校正地震波在地球内部介质中传播的路径效应.模块使用QSSP软件包（Wang et al.,2017）计算理论格林函数，然后合成理论地震图.QSSP利用广义反透射系数法（Wang,1999），数值稳定性高，在球状地球模型下的低频部分可以给出更可靠的格林函数，可以使计算地震辐射能量时的积分下限f2由原来的16.6 mHz（Di Giacomo et al.,2008）扩展到12.4 mHz（Di Giacomo et al.,2010）.

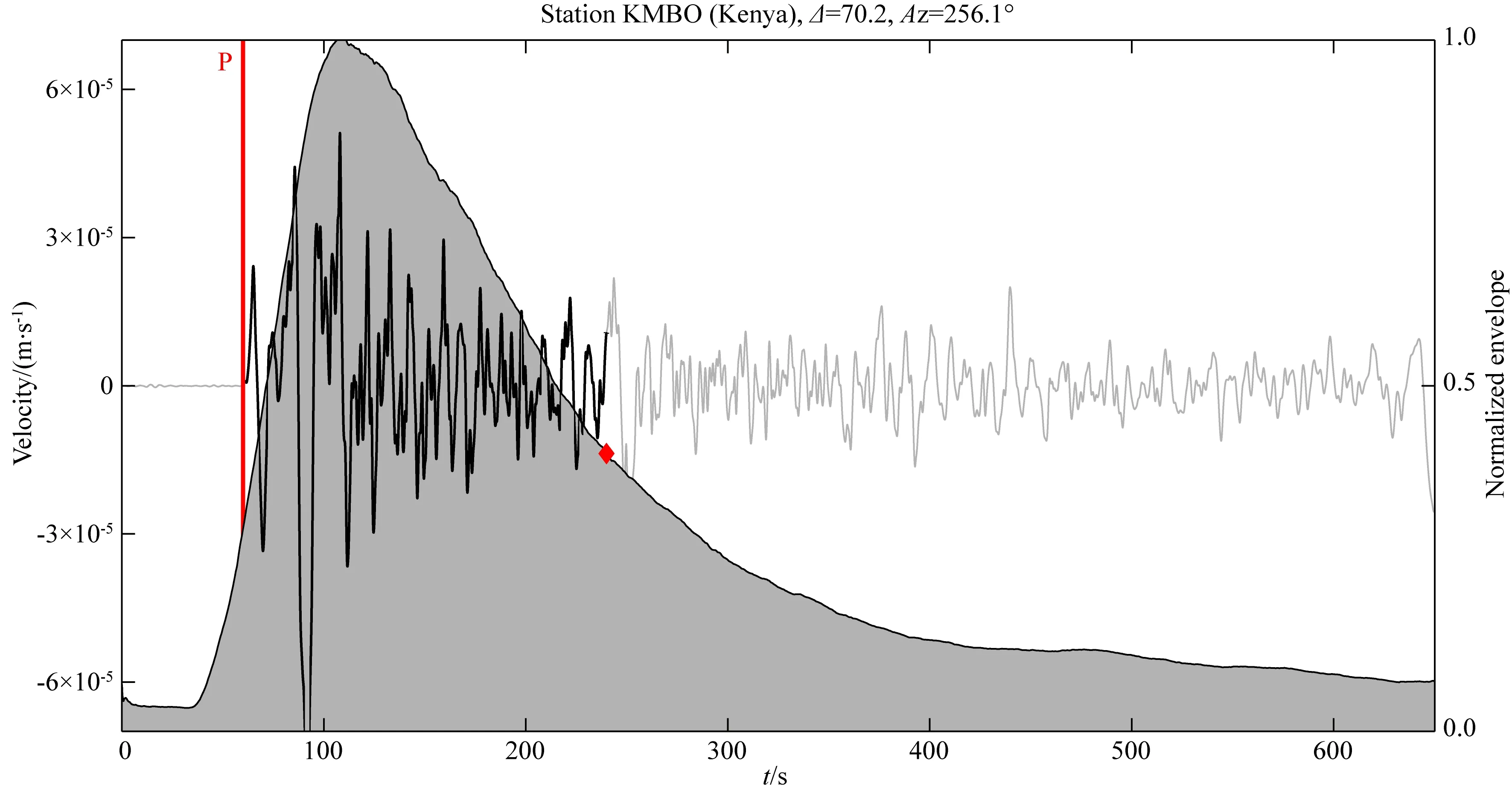
图4 汶川地震时窗长度确定过程的示例图中波形为KMBO台站记录到的汶川地震的垂直向记录.红色竖线标记了P波到时,灰色填充区域表示用于约束最终破裂持续时间的高频速度振幅包络（Bormann and Saul,2008,2009）,黑色标记的波形尾端的红色菱形符号指示了最终用于计算单台能量震级的时间窗的终止位置.Fig.4 An example of determining the time window of the Wenchuan earthquakeThe vertical component recording of the Wenchuan earthquake at station KMBO（Kenya） is shown.The P arrival time has been marked with a red line.The gray shaded area represents the envelope of high-frequency velocity amplitudes used to constrain the overall rupture time duration （Bormann and Saul,2008,2009）,and the diamond at the end of the black trace marks the end of the time window after the P-wave onset for which the final Me single station value is calculated.

（5）地震辐射能量计算模块

该模块的主要功能是计算地震辐射能量.模块通过求震源时间函数谱，并在一定频带对其积分计算地震辐射能量.

由公式（17）可知，积分频带会影响地震辐射能量的测定.地震辐射能量的计算需要在一个频率比较宽的范围对地震波在传播过程中的几何扩散（geometrical spreading）以及频率依赖的衰减（frequency-dependent attenuation）进行校正.校正频率大于1 Hz的成分时，不仅需要详细了解地球的精细结构和衰减特性，还需要详细了解台站下方的精细结构和衰减特性，这通常是不可能的.因此，一般仅计算震级大于5的地震的地震辐射能量，而且使用的是震中距大于20°的远震记录.这样做就可以通过假设平均一维层状结构来合理准确地模拟地球的过滤效果（the Earth filter effects）.AK135模型中的Q值是由周期最小为1 s的数据获得的（Montagner and Kennett,1996）.对于更短的周期，衰减函数是不可靠的.因为与实际数据相比，它们的频谱衰减太大.所以，用AK135模型计算更高频的格林函数并不合适.因此，我们将积分上限固定为1 Hz.1 Hz的限制意味着，目前我们的程序仅适用于MW>5.5的地震.但地震辐射能量的测定并不会因此受限，因为强震到特大地震的拐角频率通常都落在我们使用的频带内.并且地震辐射能量与速度的平方成正比，计算中未考虑的震源频谱部分（ff2）不会显著影响能量震级的测定，最差的情况下也仅约为0.2（Di Giacomo,2010）.积分下限f2与P波时间窗tP有关，一般不低于1/tP.

不同作者（例如,Di Bona and Rovelli,1988;Singh and Ordaz,1994;Ide and Beroza,2001）已经研究过带宽限制对能量测定的影响.尤其是Ide和Beroza（2001）指出，对于ω-2模型来说，超过80%的地震辐射能量都由高于角频率的地震波携带.Bormann和Di Giacomo（2011）总结了能量震级的低估程度与震级的关系.对那些应力降非常高并因此导致角频率fc>f2的中强地震（如MW=5.5）来说，在12.4 mHz到1 Hz带宽范围内测定地辐射能量可能造成的Me低估约为0.7.除去这一极端情况，对6.5f2）的中等到强震（5.58），能量震级的低估可能达到0.2～0.3.但是，以上数据的使用必须非常谨慎，只能作为Me可能低估范围的粗略指导.因为这些数值是从一个非常简单并常见的震源模型中获得的，并不能解释真实条件下震源频谱的复杂特性.

地震辐射能量还可以进一步转化为能量震级.在本文撰写前，李赞等（2019）已使用本程序测量了大量地震的地震辐射能量和能量震级，结果十分稳定和可靠.

3 地震辐射能量测定实例：2008年汶川8.0级地震

我们使用全球台网（Global Seismograph Network,GSN）和美国数字宽频带地震台网联合会（International Federation of Digital Seismograph Networks,FDSN）提供的宽频带垂直向P波记录，将信噪比或数据质量存在问题的台站剔除后，共有55个台站用于测定汶川地震的地震辐射能量.

汶川地震的地震辐射能量测定过程如下：将55个台站的垂直向P波记录去除仪器响应后还原为真实的速度记录；通过时窗计算模块得到汶川地震的P波时窗为180 s；由快速震源机制反演模块反演震源机制，使用QSSP计算理论格林函数并合成理论地震图；在地震辐射能量计算模块中，将每个台站的速度记录进行格林函数解卷积消除路径效应，即在频率域中求实际波形的与理论波形的频谱的比值，最后在12.4 mHz～1 Hz上对其积分得到每个台站的地震辐射能量.由地震辐射能量可以进一步得到汶川地震的能量震级，并结合地震矩和矩震级得到了能矩比、慢度系数和等效震级差等新参数（参见表1）.针对程序产出的各个地震参数，我们进行了详细分析.

表1 本文程序产出的汶川地震的地震参数Table 1 The seismic parameters calculated by the procedure of this paper

3.1 地震辐射能量

经测定，汶川地震的平均地震辐射能量为2.84×1016J，各个台站的地震辐射能量分布如图5 所示.从图中可以看出，各个台站的地震辐射能量大小并没有随震中距或方位角的变化而产生明显的分布特征.这表明使用理论格林函数法消除路径效应对不同方位角和震中距的台站的地震辐射能量测定结果的修正效果较好，使地震辐射能量的测定结果更加准确.汶川地震的破裂过程是不对称的双侧破裂过程，主要的破裂向东北方向传播了约200 km，但在东北方向300 km处也存在着较小的滑动位移量；在震中西南方向，滑动位移和破裂延伸范围总体上比较小，从而表观上表现为向北东方向的单侧破裂（陈运泰等,2009;张勇等,2009）.刘瑞丰等（2018）的研究表明，汶川地震的破裂总体上由震中向北东方向传播，由于地震多普勒效应导致震中东北方向震动加强，而震中西南方向减弱，因而在震中东北方向台站测定的面波震级偏大，而在西南方向的台站测定的面波震级偏小.如图5所示，震源东南方向的台站的地震辐射能量较大，并不是沿北东破裂方向；西南方向台站的地震辐射能量较小，与汶川地震破裂方向所产生的地震多普勒效应一致；其它两个方向的台站的地震辐射能量分布比较平均.汶川地震的地震辐射能量的分布与破裂方向性没有明显的依赖关系，这与理论格林函数法消除路径效应后的结果有一定关系.

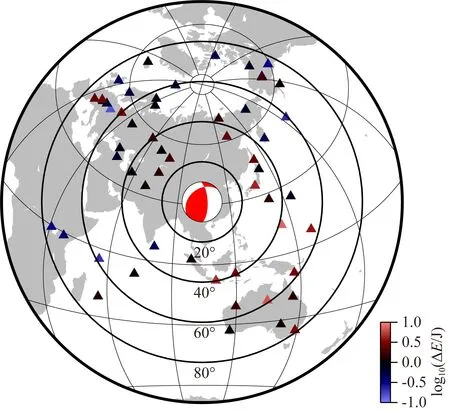
图5 汶川地震单台地震辐射能量与平均地震辐射能量差Fig.5 The difference of radiated energy for a single station with the average radiated energy of the Wenchuan earthquake

3.2 能量震级

与地震矩可以导出矩震级类似，地震辐射能量可以导出能量震级.Singh和Pacheco（1994）以矩震级为参考标度，首次提出了能量震级的概念；随后，Mayeda和Walter（1996）效仿Kanamori（1977）也引入了能量震级.Choy和Boatwright（1995）通过测定400个地震的地震辐射能量，用类似地震矩标定矩震级的方法，重新标定了地震辐射能量和震级的经验关系：

lgER=1.5MS+4.4，

（18）

通过这一经验关系给出了能量震级计算公式：

（19）

我们可以通过公式（19）计算汶川地震的能量震级.需要说明的是，根据单台辐射能量直接求得的平均辐射能量离散度比较大，会使得到的能量震级结果变得不可靠.因此，我们先将各个台站的辐射能量转化为能量震级，再求所有台站的能量震级的算数平均值，这样可以避免辐射能量离散较大对能量震级最终测定结果的影响.最后，我们得到汶川地震的平均能量震级为8.04，标准差为0.25.图6给出了各个台站的震中距和相应的能量震级.从图中可以看出，各个台站的能量震级不随震中距的变化而改变，说明使用理论格林函数法消除路径效应对地震辐射能量的测定结果的修正效果较好.

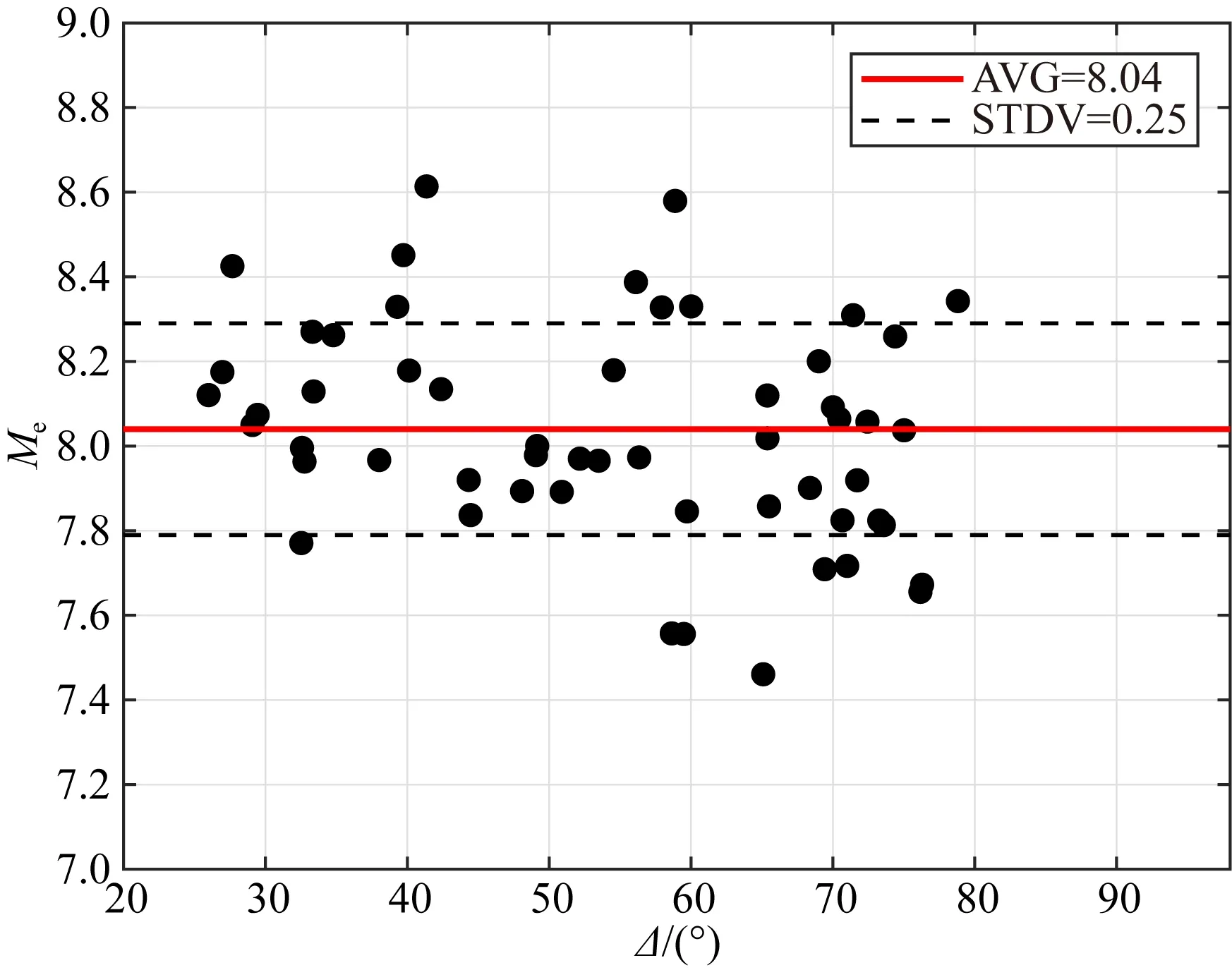
图6 汶川地震各台站的能量震级随震中距（Δ）的分布Fig.6 The distribution of energy magnitude of each station with epicenter distance of the Wenchuan earthquake

表2给出了不同机构和作者测定的汶川地震的能量震级.Di Giacomo（2010）在测定能量震级时假设没有断层面和几何滑动的先验信息，而是使走向、倾向和倾角以15°的步长在震源球上变化，计算每个距离上由震源参数（走向、倾向和倾角）的不同组合产生的一组时间序列，这种做法相当于对震源机制进行一种近似平均处理.USGS使用Boatwright和Choy（1986）的方法计算能量震级，这种方法需要了解断层面解和深度，以对特定的辐射花样进行校正.本文利用快速震源机制反演出的结果对震源进行校正，并使用理论格林函数法消除路径效应.由表2可知，本文结果与USGS的结果基本一致，与Di Giacomo（2010）的结果略有差别.与USGS相比，虽然在消除路径效应时使用的方法不同，但我们在计算能量震级时都对震源进行了一定程度的约束.Di Giacomo（2010）对震源进行了近似平均处理，与实际震源仍有一定差别，得到的结果与我们略有不同.由于USGS并未公布各个台站能量震级的详细测定结果，因此，无法得到它们的残差.Di Giacomo（2010）的残差分布由最小的0.27（震中距50°～60°）到最大的0.328（震中距20°～30°）不等，同样使用理论格林函数法消除路径效应，本文测定结果的标准差为0.25，较之更为稳定.通过以上对比可知，震源机制会对能量震级测定产生影响，合适的震源机制校正可以提高测定结果的稳定性和可靠性.值得注意的是，Di Giacomo（2010）的目的是提出一种能量震级快速测定方法，以达到实时测定全球浅源地震的能量震级的目的，对于计算过程中的一些近似处理都以满足快速测定的误差要求为准.Boatwright和Choy（1986）的方法采用修正过的并且精确的深度和震源机制解（来自宽频带波形模拟或矩张量解），这使USGS需要更长的时间才能发布能量震级.本文自主开发的能量震级快速测定程序可以在发震后接收到波形数据时快速完成震源机制反演，一定程度上兼顾了时效性和准确性.

表2 不同机构和作者发布的汶川地震的能量震级（单位：Me）Table 2 The energy magnitude of Wenchuan earthquake from different author and organization

3.3 震源机制解

在快速震源机制反演模块中，在30°～90°震中距范围内的GSN与FDSN台站中，按噪声水平、台站分布逐级筛选了42个台站的长周期垂直分量（LHZ）数据.利用快速震源机制反演方法（张喆和许力生,2021）对0.005～0.01 Hz频带内的位移数据进行反演，得到了汶川地震的震源机制解（表3）.其中，地震矩M0为8.97×1020N·m，相当于矩震级MW7.9.为了检验反演结果的可靠性，我们将理论地震图与观测波形进行了对比（图7）.大多数台站的相关系数都在0.90以上，二者的平均相关系数达到0.91，表明我们反演得到的震源机制解比较准确.

表3 汶川地震的震源参数Table 3 The source parameters of the Wenchuan earthquake

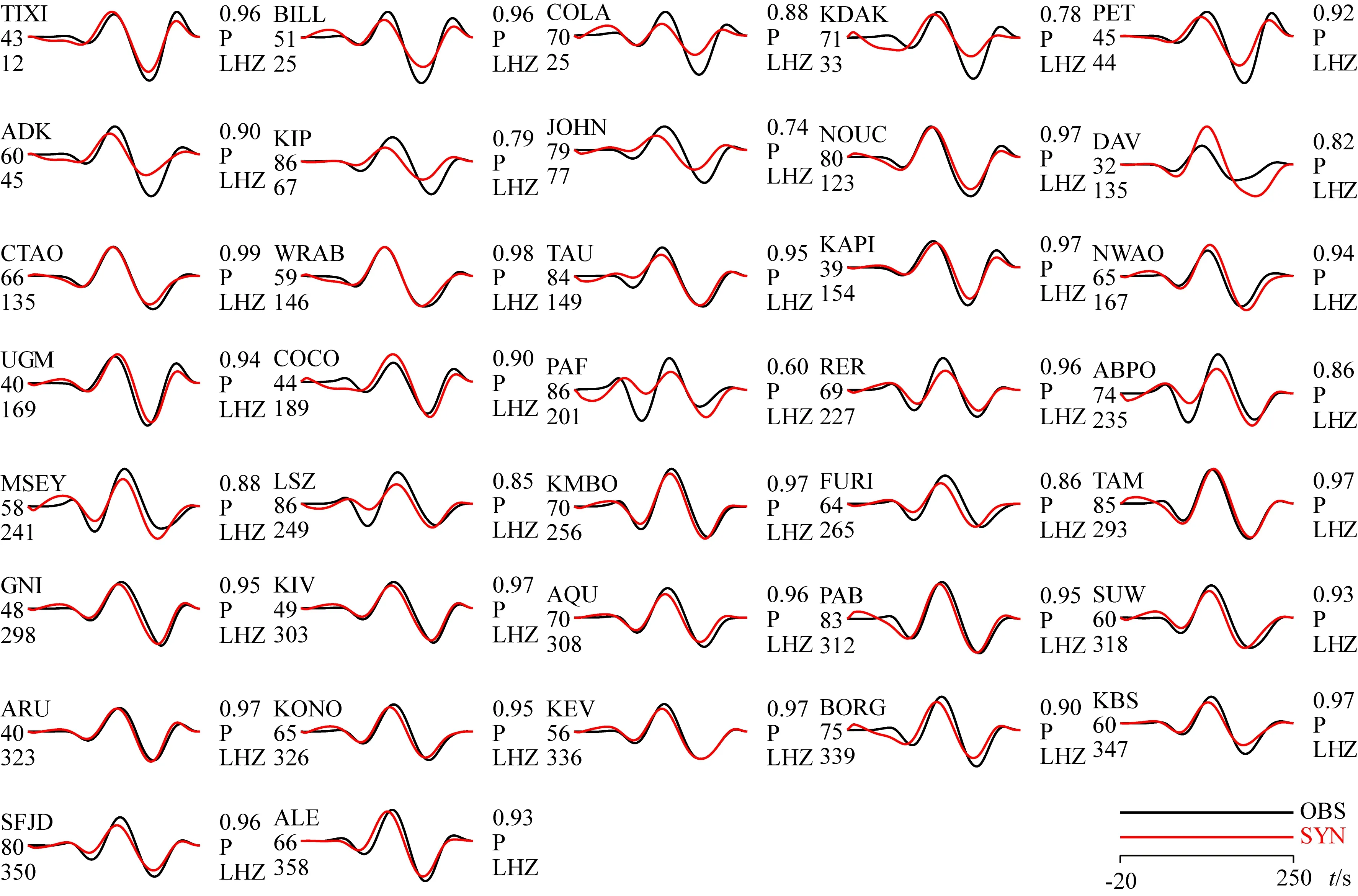
图7 观测波形与理论地震图的比较每幅子图左侧从上至下依次为台站名,震中距和方位角,右侧从上至下依次为相关系数和震相名.波形滤波频带为0.005～0.01 Hz.Fig.7 The comparison of observed waveforms with theoretical seismogramOn the left side of the subplot are station code,epicentral distance,and station-azimuth,respectively,and on the right side are the correlation coefficient and phase name,respectively.A frequency band of 0.005～0.01 Hz is used.

3.4 能矩比

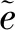
（20）

能矩比是反映地震辐射能量释放效率的重要参数，通过计算能矩比可以了解汶川地震的能量释放效率.本文测定的汶川地震的地震矩为8.97×1020N·m，地震辐射能量为2.84×1016J，由公式（20）可得汶川地震的能矩比为3.17×10-5.全球M≥5.8浅源地震的平均能矩比为1.2×10-5（Choy et al.,2006），其中，走滑型地震的平均能矩比为4×10-5（Convers and Newman,2011），逆冲型地震的平均能矩比为0.8×10-5（宋金,2020）.由以上数据对比可知，汶川地震的能矩比约为全球平均能矩比的2.6倍；略低于走滑型地震的平均能矩比；远高于逆冲型地震的平均能矩比，约为其4倍.Choy等（2006）指出走滑型地震的平均能矩比远高于逆冲型地震.而汶川地震是以逆冲断层为主的地震，其能矩比仅略低于走滑型地震的平均能矩比.说明与一般逆冲型地震不同，汶川地震的能量释放效率异常高，与它造成的巨大破坏相匹配.综上所述，汶川地震属于能量释放效率明显偏高的逆冲型地震，即与相同地震矩的地震相比，汶川地震释放的地震辐射能量更大，在其它因素相差不大的情况下引起的地震动更大、造成的破坏更大.即使是同一地震构造区发生的具有非常相似震源机制和地震矩的地震，也可能存在显著不同的地震辐射能量（Di Giacomo et al.,2010;李赞等,2019;宋金等,2020;王子博等,2021）.因此，仅通过分析地震矩这一单一的静态参数难以全面、直观地反映地震造成的灾害程度.而地震辐射能量是一个与震源直接相关且具有明确物理意义的重要地震参数，可以有效弥补地震矩在评估地震灾害和危险性上的不足.

3.5 慢度系数

能矩比取对数可以得到新的地震参数，慢度系数Θ（Newman and Okal,1998）：

（21）

与动辄需要用科学计数法表示的能矩比相比，慢度系数能够更直观地显示地震辐射能量的释放效率，更符合非专业人士对“大小”的认知.汶川地震的能矩比为3.17×10-5，由公式（21）可得慢度系数为-4.50.

对于应力降明显不同的地震，Θ不是一个固定的常数，其变化范围在-3.2～-6.9，全球浅源地震的平均慢度系数约为-4.92，走滑型地震的平均慢度系数约为-4.39，逆冲型地震的平均慢度系数约为-5.09.通过以上数字可以快速分辨汶川地震的地震辐射能量释放效率在所有类型地震中所处位置，这一优势使慢度系数较能矩比更适合在普通群众中推广.

3.6 等效震级差

Choy（2012）在慢度系数的基础上提出了等效震级差ΔM的概念：

ΔM=Me-MW，

（22）

用于区别地震辐射能量异常高、中等和异常低的地震，是快速评估地震危害和损害类型差异的重要判定参数.当ΔM≥0时，地震辐射能量异常高；当ΔM<-0.5时，地震辐射能量异常低，汶川地震的等效震级差为0.14，属于地震辐射能量异常高的地震.

同时测定能量震级和矩震级并计算等效震级差，可以快速分析地震辐射能量的释放情况，进而评估地震危险性.因此，在地震发生后快速测定并发布能量震级十分重要.矩震级虽然不受震级饱和效应影响，但矩震级对应的地震矩仅代表断层错动的“零频”（静态位错）成分大小，与位错的时间历程无关，从而无法反映地震的动态破裂过程.除地震断层错动的零频信息外，还需考虑震源谱上各种频率尤其是高频信息.所以，仅凭矩震级难以全面评估地震的振动效应.而地震辐射能量是对全频段震源谱的平方积分，侧重反映震源辐射的高频分量，描述了地震的动态破裂过程，由地震辐射能量导出的能量震级比矩震级更适合描述地震的潜在破坏性（Boatwright and Choy,1986;Bormann et al.,2002;Choy and Kirby,2004）.

4 结论

本文开展了地震辐射能量测定方法的研究，从地震辐射能量测定公式的推导出发，自主开发了地震辐射能量和能量震级快速测定的软件系统，包含数据处理、时窗计算、快速震源机制反演、理论格林函数计算和地震辐射能量计算五个主要模块.我们以汶川地震为例展示了程序各模块的主要功能和计算过程，通过对结果的分析和讨论，得到以下研究结论：

（1）利用55个台站的远场P波资料测定出汶川地震的地震辐射能量为2.84×1016J，各个台站的地震辐射能量与方位角和震中距没有明显的依赖关系，理论格林函数有效地消除了地震波在地球介质中传播时产生的路径效应.

（2）汶川地震的能量震级为8.04，标准差为0.25.本文的测定结果与USGS发布的结果高度一致，与Di Giacomo的结果略有差别.我们与USGS在测定地震辐射能量时都对震源进行了一定程度的约束，相比于Di Giacomo对震源进行的近似平均处理，更为接近实际震源.能量震级测定结果的残差分析表明，震源机制校正可以使能量震级的测定结果离散更小、更稳定.因此，有必要在测定能量震级时加入震源机制校正.

（3）通过快速震源机制反演得到汶川地震的震源参数：地震矩为8.97×1020N·m，转化为矩震级为7.9；震源机制解：节面Ⅰ走向231°、倾角35°、滑动角138°，节面Ⅱ走向357°、倾角68°、滑动角63°.使用该震源机制解合成理论地震图并与观测波形对比，结果显示，大多数台站的相关系数在0.9以上，二者平均相关系数达到0.91，表明反演出的震源机制解较为可靠.

（3）汶川地震的能矩比为3.17×10-5，约为全球浅源地震平均能矩比的2.6倍，略低于全球走滑型地震的平均能矩比，约为全球逆冲型地震平均能矩比的4倍.汶川地震属于能量释放效率非常高的逆冲型地震，即与相同地震矩的地震相比，汶川地震释放的地震辐射能量更大，在其它因素相差不大的情况下引起的地震动更大、造成的破坏更大.

（4）能矩比取对数可以得到新的地震参数慢度系数.汶川地震的慢度系数为-4.50，高于全球浅源地震的平均慢度系数-4.92和逆冲型地震的平均慢度系数-5.09，略低于走滑型地震的平均慢度系数-4.39.慢度系数可以更直观地显示地震辐射能量释放效率的高低，符合非专业人士对地震“大小”的认知，更适合在普通群众中推广.

（5）汶川地震的等效震级差为0.14，属于地震辐射能量异常高的地震.同时测定矩震级和能量震级才能计算等效震级差.能量震级可以弥补矩震级在描述地震动态破裂过程上的不足，联合测定矩震级和能量震级能够更全面地评估地震的灾害危险性.

致谢感谢两位匿名审稿专家和责任编委对本文提出的宝贵意见.本文使用的数据来自地震学联合研究会（IRIS）数据中心，部分图片由GMT（Wessel et al.,2019）绘制.