基于重磁泊松定理的磁化方向估计及应用：以相山铀矿田为例

王彦国，邓居智，葛坤朋，刘祜

1 东华理工大学核资源与环境国家重点实验室，南昌 330013 2 东华理工大学地球物理与测控技术学院，南昌 330013 3 核工业北京地质研究所，北京 100029

0 引言

磁法数据处理与解释是磁法勘探的核心环节，但磁异常受磁化方向影响，与地质体没有明显的对应性，直接进行异常解释难度较大.化极处理可以将斜磁化感磁异常转换为垂直磁异常，在一定程度上有助于异常的解释与推断（罗潇等，2021；张志厚等，2021；韩梅等，2022）.然而，当研究区存在与现代地磁场方向不一致的强剩磁时，磁异常往往较为复杂，化极很难获得满意的效果（王妙月等，2004）.此时，确定出地质体的磁化方向对于磁法数据处理、正反演计算及解释推断具有重要意义（谢汝宽等，2021）.目前，磁化方向估计的方法主要有三类：互相关估算法、磁矩积分法、重磁相关分析法.

互相关估算法主要是通过试算不同的磁化倾角与偏角下的化极数据与另一种少受磁化方向影响的转换数据进行互相关计算，寻找出最大相互系数时的磁化方向.Roest 和Pilkington（1993）利用2维磁解析信号与磁源重力异常水平梯度的互相关进行了磁化方向估计；Nicolosi 等（2006）利用不同磁化方向上的平均等效源正演磁异常与实测磁异常进行互相关计算来获取最佳的磁化方向；Dannemiller 和Li （2006）利用不同磁化方向下的化极磁异常垂向导数与磁解析信号的互相关估计磁化偏角与倾角；Gerovska等（2009）利用总磁异常强度与不同磁化方向上的化极异常进行互相关来估算磁源磁化方向；Guo等（2014）使用归一化磁源强度与不同磁化角度下的化极数据开展互相关计算；Zhang等（2018）则是在归一化磁源强度的垂向导数及不同磁化角度下的化极异常垂向导数的互相关基础上估算磁化方向.这类估算地质体磁化方向的方法，主要是针对单一场源或磁化方向相同的多场源进行，或者是根据磁异常特征对研究区进行分区计算，另外方法受低纬度化极影响较为严重.

磁矩积分法是利用三分量磁异常与对应坐标乘积的平面积分来获取不同方向上的磁矩，进而计算出磁化方向.Helbig（1963）提出了场源三分量磁异常积分与一阶磁矩的关系式；管志宁和李保国（1984）在一阶磁矩表达式基础上推导出了二阶磁矩积分，并提出了磁源总磁矩、中心位置及磁化方向估计的迭代算法；Phillips（2005）在Helbig（1963）研究基础上，利用网格数值积分近似代替无穷积分，并采用滑动窗口计算场源磁化方向；Foss 和McKenzie （2011）详细探讨了窗口大小对磁化方向估计结果的影响；谢汝宽（2021）等在Phillips（2005）的研究基础上，采用了限定估算区域方法来避免叠加异常的相互影响，获得了叠加异常下的各个场源磁化方向.但这类方法需要具备磁异常三分量，限制了在仅有总磁异常强度地区的使用.另外计算窗口的选择也是一个关键问题，窗口选择过大，则易受叠加异常影响，窗口选择过小，则积分区间不足，都会严重影响磁化方向估计的精度.

重磁相关分析法是从重磁泊松定理出发，利用重磁场的相关性来研究地质体的磁化方向.Garland（1951）首先提出了重磁泊松定理，并用于确定单一地质体磁化强度与密度的比值；Cordell和Taylor（1971）建立了波数域重磁泊松公式，结合重力异常和磁源重力异常振幅谱，用于计算垂直磁化下的柯尼希斯贝格比（剩磁与感磁比）及总磁化方向；Bilim和Ates（1999）采用不同磁化方向转换的磁源重力异常与观测重力异常进行均方误差计算，将最小均方误差对应的磁化方向做为最终结果.目前，该类方法主要是针对单一场源进行的，难以用于磁化方向不一致的多场源叠加重磁异常的计算中.

本文在重磁泊松定理基础上，推导出了磁异常一阶导数、重力位三阶导数、地磁场方向及场源磁化方向之间的关系式，并构建了求解磁化强度三分量的线性方程组，进而获得了重磁同源体的磁化方向.本文方法无需进行化极处理，无需事先已知场源物性及位置信息，可以快速地反演出叠加重磁场下的各个场源磁化方向.文中通过模型试验验证了方法的正确性和有效性，同时应用于了江西相山铀矿田的重磁数据之中，获得了多个测算点上的磁化方向，并对反演结果进行了解释推断.

1 基本原理

对于均匀磁化场源，其重力位与磁位可用泊松定理（Garland，1951）予以描述：

（1）

其中U、V分别是磁位和重力位，ρ为剩余密度，Mx、My和Mz是磁化强度M在x、y、z三个方向上的分量，G为万有引力常数.

磁感应强度的三个分量可由磁位求得：

（2）

其中u0为真空中导磁率.

磁异常ΔT可由磁感应强度三个分量表示：

（3）

其中αT、βT、γT是现代地磁场强度与x、y、z三个坐标轴之间的夹角，可由地磁倾角I0与偏角D0表示，即：cosαT=cosI0cosD0，cosβT=cosI0sinD0，cosγT=sinI0.

求磁异常的x、y、z三个方向导数，得：

（4）

（5）

（6）

令：

（7）

则公式（4）—（6）可改写为：

（8）

显然通过求解方程组（8）可得到每个测点的Mx、My和Mz.但为了使计算结果更加可靠，可采用滑动窗口实现.若窗口内的数据点数为n，构建的超定方程组为：

（9）

利用最小二乘法求解公式（9）即可得到磁化强度的三个分量.

获得磁化强度三分量后，场源磁化倾角IM与磁化偏角DM可分别表示为：

（11）

该方法的计算流程为：

（1）利用波谱转换将重、磁异常换算出重力位三阶混合偏导数和磁异常一阶导数.

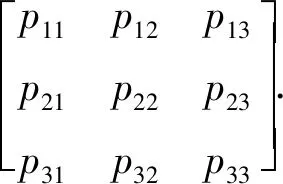
（3）给定一个计算窗口，利用公式（9）对工区进行全覆盖计算，获得磁化强度三个分量Mx、My和Mz.这里需要指出的是，公式（9）中还包含未知数ρ，在计算中可事先给定剩余密度ρ=1 g·cm-3即可.这是由于计算场源磁化方向时，利用了比值计算，消除了密度ρ大小的影响.

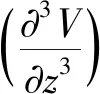
2 模型试验

2.1 单一模型试验

为了验证本文方法的正确性，首先设计了一个单一球体模型，埋深为1 km，半径为0.5 km，剩余密度为1 g·cm-3，磁化强度为 1 A·m-1，磁化倾角和偏角均为-45°.地磁场强度为48000 nT，地磁倾角为45°，地磁偏角为-5°.设计的测线长度为10 km，测线101条，测网密度为0.1 km×0.1 km.图1a、b是模型体产生的重力异常与磁异常，图1c、d则是利用0.5 km×0.5 km（25个数据）的滑动计算窗口获得的整个试验区内磁化倾角与偏角.图中可以看出，在模型体及外围一定区域内，反演获得的磁化倾角和偏角都在-45.5°～-44.5°之间，而球体模型质心位置，磁化倾角与偏角的反演结果均是-45°，与理论值完全重合.该试验表明了本文算法是可行的.

2.2 组合模型试验

为了检验本文方法在复杂情况下的应用效果，设计了一个包含5种类型场源的组合模型，各模型参数见表1，模型体相对位置见图2.所有模型体均处于强度为48000 nT，磁倾角为45°，磁偏角为-10°的地磁场之中.图3a、b分别是组合模型产生的理论重力异常与磁异常，其中网格间距为0.1 km×0.1 km.可以看出，受叠加异常影响，球体和岩珠的重力异常极小值与场源质心位置不重合，而受磁化方向影响，磁异常与场源并无明显的对应关系.

图4a、b分别给出了重力垂向二阶导数和磁一阶解析信号图.可以看出，重力异常的极值点与场源位置存在良好的对应性，磁解析信号极大值可以反映出球体、岩珠、棱柱体位置，但极值位置与模型体中心位置存在一定偏差，这主要是解析信号仍在一定程度上受磁化方向影响.不过，磁解析信号极大值可以较好地反映出岩脉位置及薄层边界位置.图4c、d是反演得到的场源磁化倾角与磁化偏角，其中选择的计算窗口为0.5 km×0.5 km.为了更加合理地评价反演结果，图中给出了重力垂向二阶导数（∂3V/∂z3）极值点及磁解析信号极大值点处的反演结果，以及场源周围一定区域的反演值构成的磁化倾角与偏角等值线图及平均估计值.从反演结果中可以看出，无论是重力极值点、磁解析信号极值点、还是平均估计值，三者都较为接近，均与理论磁化角度相近，反映了在复杂条件下，本文方法仍是有效的、可行的.反演误差主要来自于异常叠加的影响，另外磁化偏角的偏差比磁化倾角的大些.

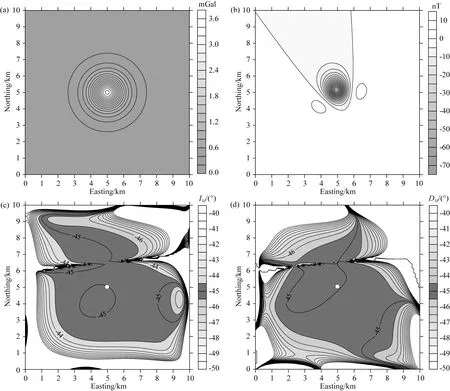
图1 单一球体模型试验（a） 重力异常；（b） 磁异常；（c） 磁化倾角估计值；（d） 磁化偏角估计值.Fig.1 Model test for one single sphere（a） Gravity anomaly;（b） Magnetic anomaly;（c） The estimated magnetization inclination;（d） The estimated magnetization declination.

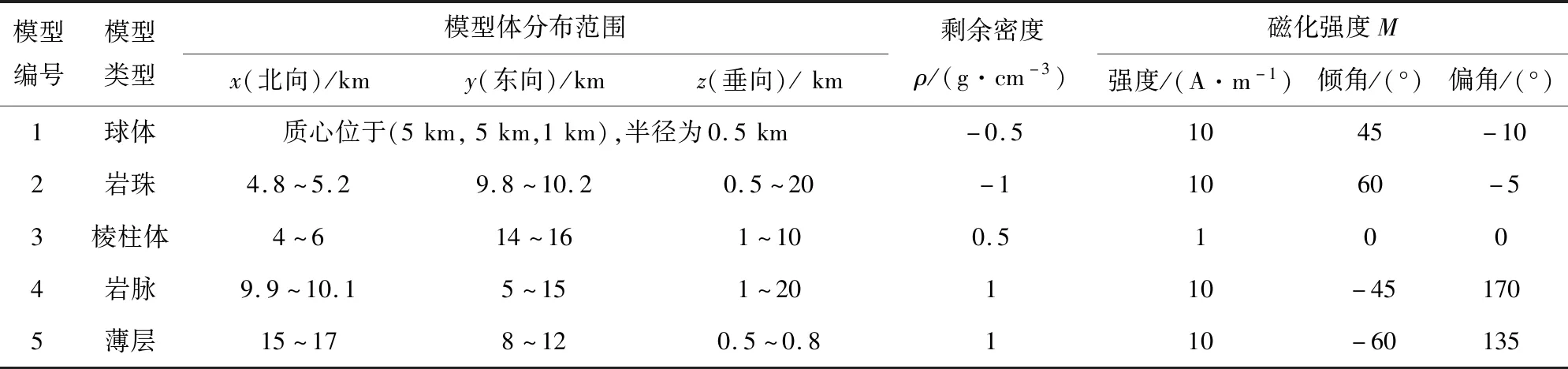
表1 组合模型参数Table 1 Parameters of multi-sources

为了反映本文方法的优越性，选择了Dannemiller和Li（2006）提出的不同磁化方向下化极磁异常垂向导数与解析信号的互相关系数估计磁化方向的方法进行对比.本文中该方法的计算过程为：首先选取磁化倾角与磁化偏角间隔均为5°，然后利用不同磁化方向对整个区域的磁异常进行化极、垂向导数及解析信号计算，最后根据图3b中各个模型的异常区域计算互相关系数，结果见图5.可以看出，相关系数的极大值基本真实地反映出球体1、岩珠2及薄层5的磁化方向，但是在棱柱体3上有3个明显的极大值，在岩脉4上有2个极大值.另外，表2给出本文方法在重力二阶垂向导数极值点处磁化方向反演结果及Dannemiller和Li（2006）方法的磁化方法估计结果，易看出，本文方法计算的磁化方向误差更小，尤其磁化倾角计算精度明显大于Dannemiller和Li方法的.

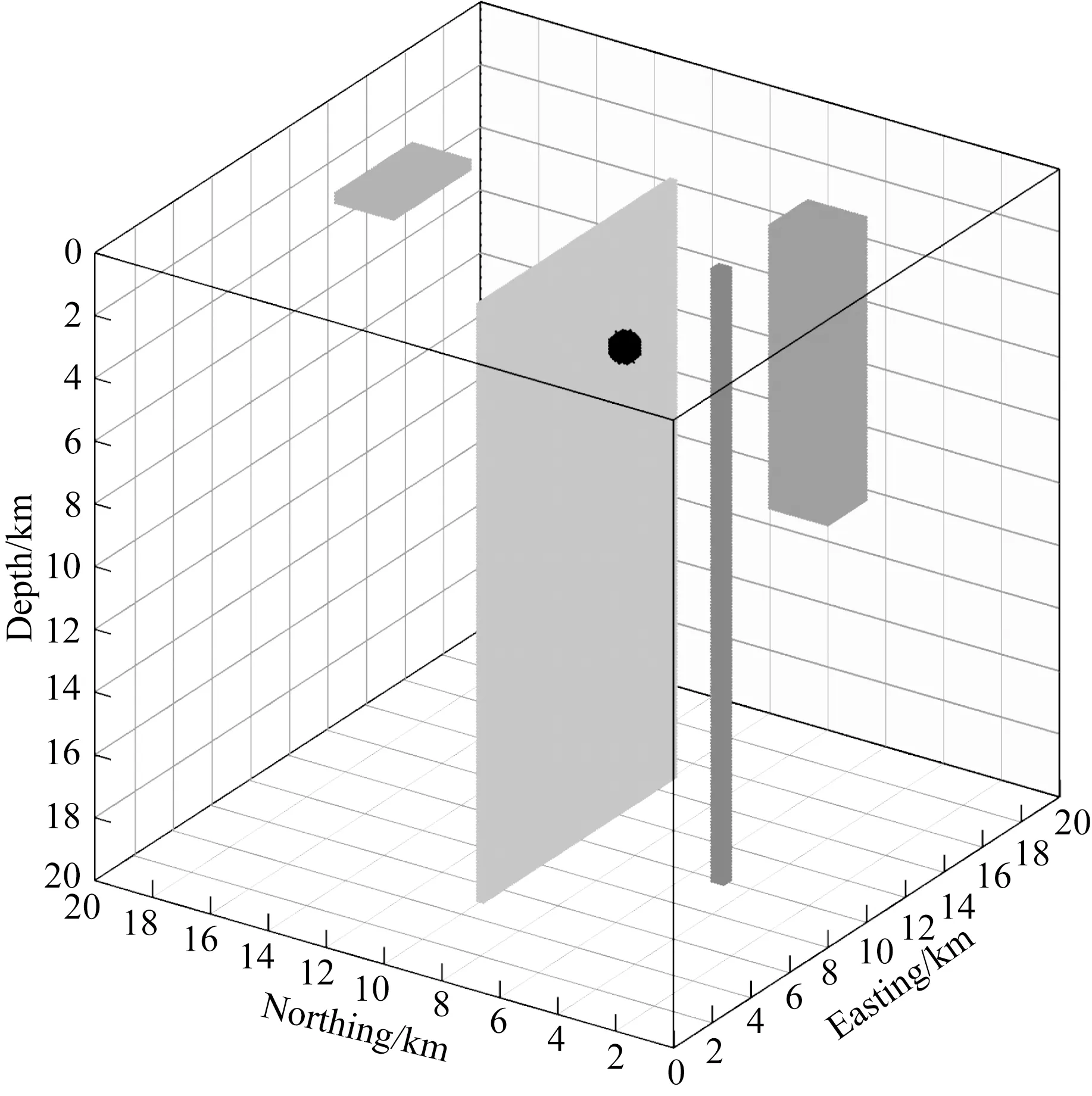
图2 组合模型立体分布图Fig.2 Stereogram of synthetic model

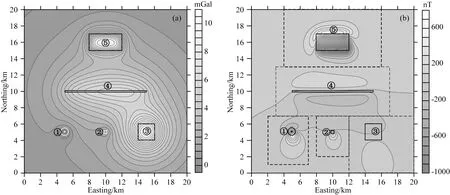
图3 组合模型的正演重磁异常（a） 重力异常；（b） 磁异常.实线是模型体边界；虚线是为实现Dannemiller 和Li （2006） 方法圈定的不同模型体异常区范围.Fig.3 Forward gravity and magnetic anomalies of multi-sources（a） Gravity anomaly;（b） Magnetic anomaly.The solid lines are boundaries of the models,and the dotted lines show the target anomalies of the models for the method presented by Dannemiller and Li,2006.

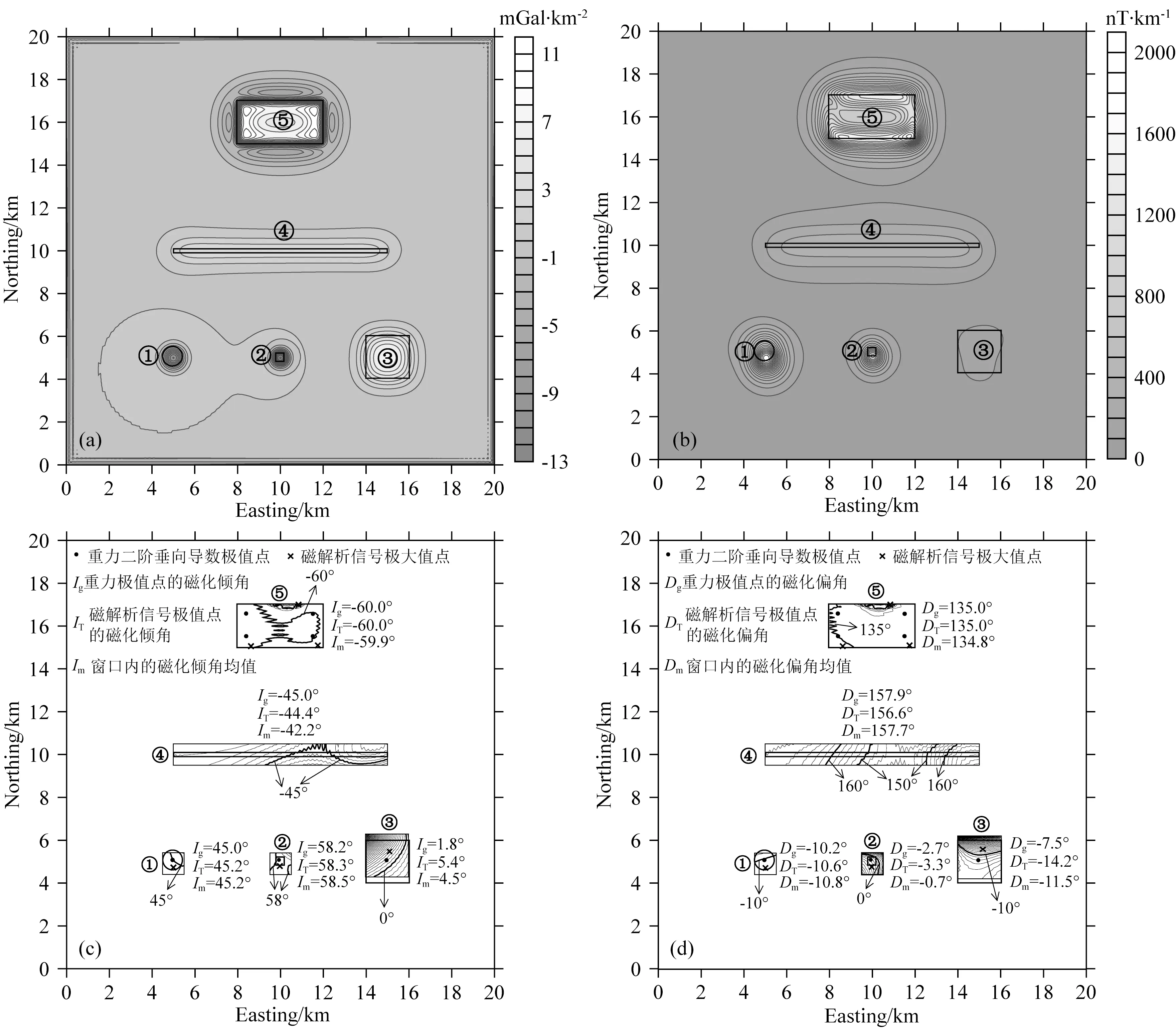
图4 组合模型的磁化方向估计结果（a） 重力垂向二阶导数；（b） 磁解析信号；（c） 磁化倾角估计值；（d） 磁化偏角估计值.Fig.4 The estimated magnetization directions of multi-sources（a） The second-order vertical derivative of gravity anomaly;（b） The analytic signal of magnetic anomaly;（c） The estimated magnetization inclination;（d）The estimated magnetization declination.

为了了解噪声干扰对本文算法的影响，对叠加重、磁异常（图3a、b）均添加了1%的随机噪声（图6a、b），易看出噪声明显引起了重、磁异常等值线的不规则波动.图7a、b是直接利用波谱转换得到的重力垂向二阶导数和磁异常解析信号，可以看出，受噪声影响，重力垂向二阶导数的有效异常完全淹没在噪声干扰之中，已无法识别出场源的异常信息；由于磁解析信号只求取了磁异常的一阶导数，因此受噪声影响有限，还可以看出球体、岩珠、岩脉及薄层的异常信息，但棱柱体异常较弱，同样被噪声所覆盖.由于直接换算得到的重力位三阶导数和磁异常一阶导数受噪声影响严重，直接进行磁化方向反演已完全失效，因此这里不予展示.

为了削弱噪声的影响，将重、磁异常分别向上延拓了0.3、0.5、0.7 km，然后再进行磁化方向反演工作.表2给出了不同延拓高度时本文方法和Dannemiller和Li方法的磁化方向估计结果.可以看出：（1）含噪异常经过向上延拓处理后，两种方法的计算精度相对于无噪声时都有所下降；（2）三个延拓高度下，本文方法得到的磁法方向（尤其磁化倾角）精度都高于Dannemiller和Li方法；（3）两种方法均在向上延拓0.5 km时，磁化倾角的估计精度最高，不过本文方法估计的磁化倾角精度明显高于Dannemiller和Li方法的，而且Dannemiller和Li方法仍会在棱柱体上方获得多个磁化方向；（4）虽然向上延拓0.5 km时，两种方法效果均最好，但其他延拓高度下的磁化方向计算结果同样是可信的，也就是说，在一定延拓高度内，选择不同延拓高度的计算结果都是可行的.图7c、d是延拓0.5 km后的重力垂向二阶导数及磁解析信号.可以看出，此时重力垂向二阶导数和磁解析信号的稳定性获得了较大幅度的提升，异常的极值也能很好地反映场源位置.图7e、f是本文方法获得的磁化方向反演结果，可以看出，无论是重力垂向二阶导数极值点、磁解析信号极值点，还是场源附近区域内平均值，估计得到的磁化倾角比较接近，也与理论值较为吻合，不过重力垂向二阶导数极值点处的估计值更加准确些.相对于无噪声时的反演结果，各个模型体上的磁化方向估计误差都有所增加，这主要是重、磁异常进行向上延拓处理后，叠加异常的相互影响更加严重导致的.图8给出了向上延拓0.5 km时Dannemiller和Li方法在各个模型体上的磁化方向估计结果，对比无噪声时反演结果可以看出，除了在岩珠上磁化方向误差明显增加外，其他模型体上的磁化方向估计值与无噪声时基本相同，不过该方法仍在棱柱体上获得了3个磁化方向.该试验结果表明，在重、磁异常中无噪声时，本文方法可以很好地估计出叠加模型下各个场源的磁化倾角与磁化偏角，Dannemiller和Li（2006）提出的磁化方向试算方法同样可以较好地估计出磁化方向，但精度明显低于本文方法的，而且会出现多解情况；当重、磁异常含有噪声时，经向上延拓处理后，虽然磁化方向的估计误差会有所增加，但仍能有效地反演出场源的磁化方向，而小规模场源（如岩珠）的磁化方向估计误差会明显增加，另外本文方法的磁化倾角估计精度仍明显高于Dannemiller和Li方法的.

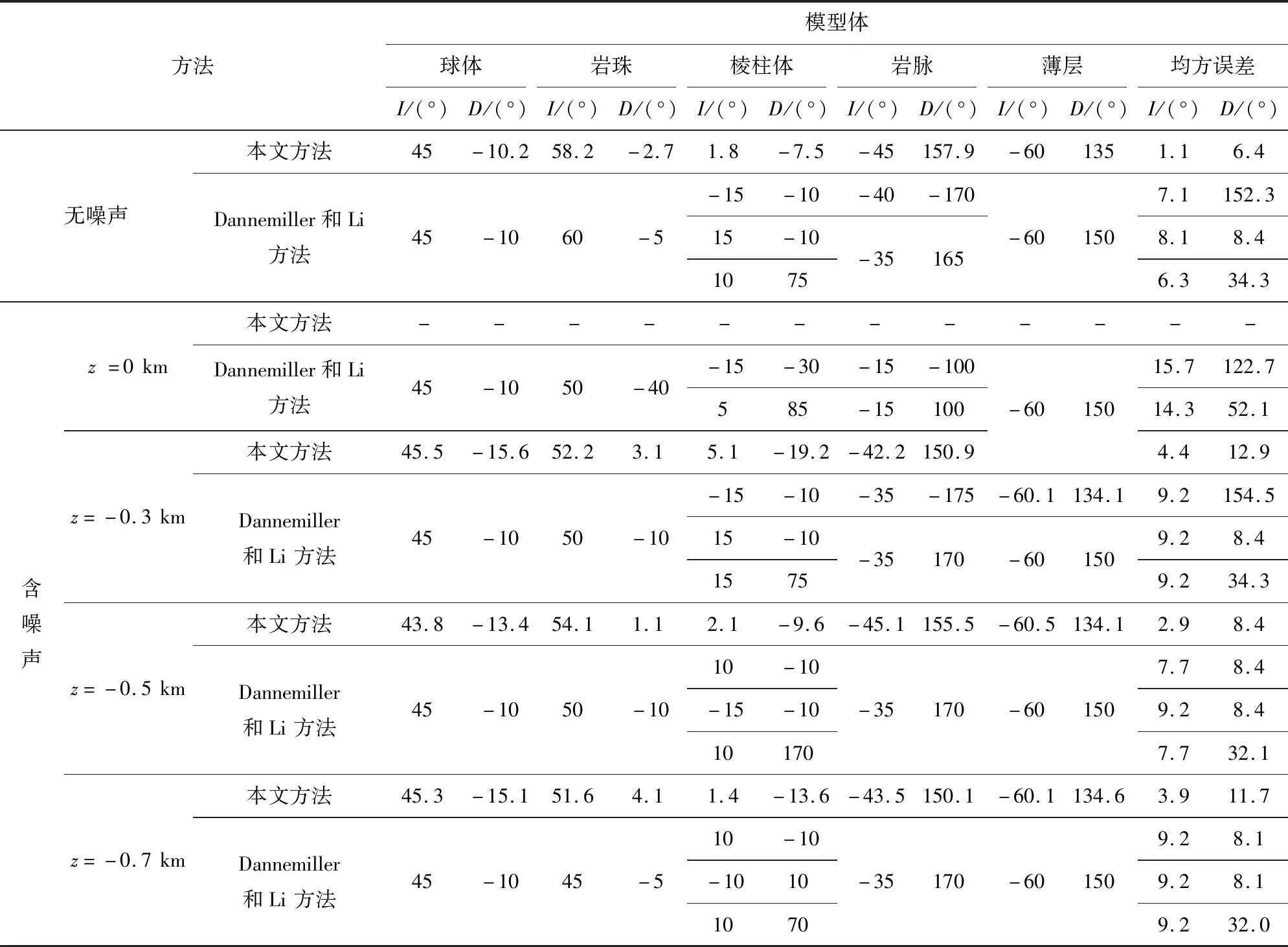
表2 两种磁化方向估计方法在组合模型磁异常无噪声干扰及含噪声时延拓不同高度（z）的计算结果Table 2 The estimated magnetization directions of different models using two methods when the magnetic anomaly including noise-free and noise-corrupted but by upward continuation of different altitudes

图5 基于不同磁化方向下化极磁异常垂向导数与解析信号相关系数的磁化方向估计结果（a） 球体1；（b） 岩珠2；（c） 棱柱体3；（d） 岩脉4；（e） 薄层5.Fig.5 The estimated magnetization directions of different models using the correlation between the vertical derivative and the analytic signal of the reduced-to-pole field（a） Sphere 1；（b） Stock 2；（c） Prism 3；（d） Dike 4；（e） Sheet 5.

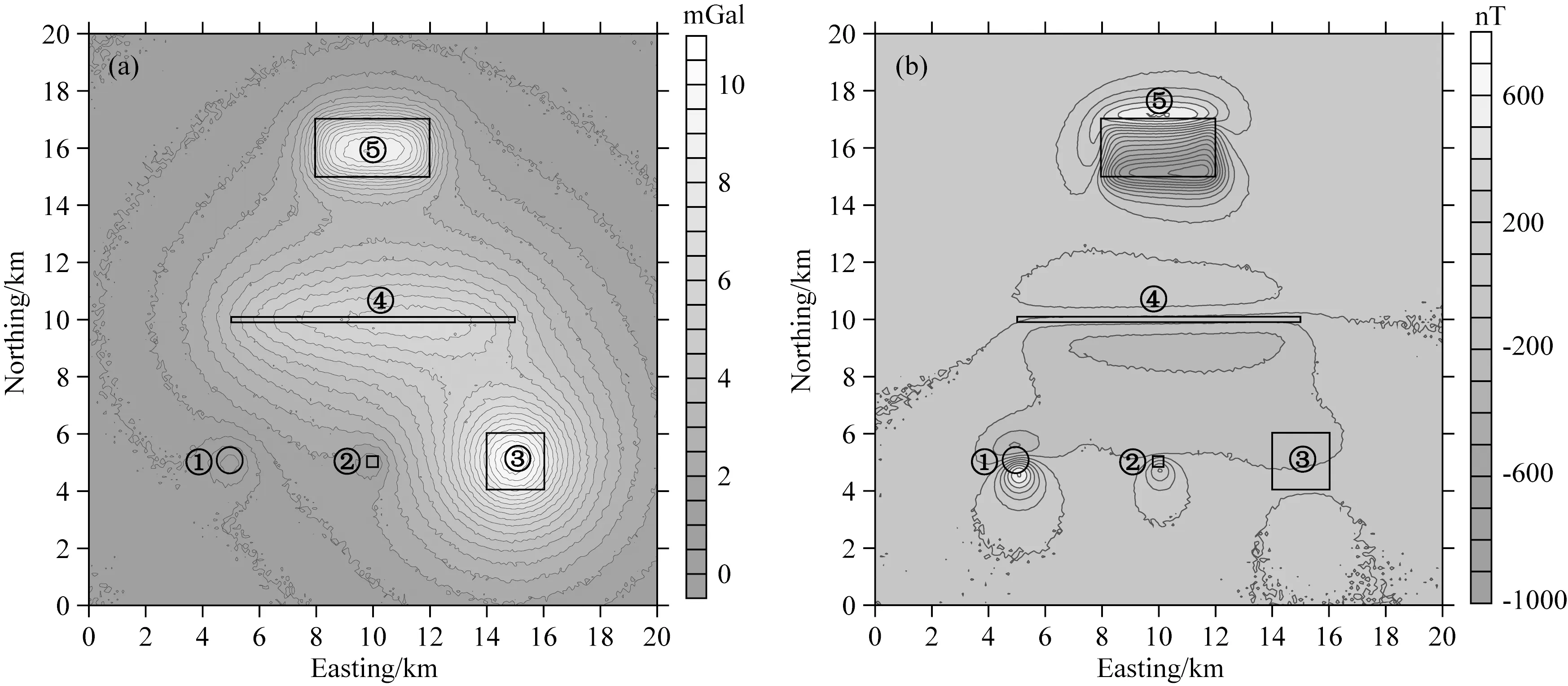
图6 含1%噪声的组合模型重磁异常（a） 重力异常；（b） 磁异常.Fig.6 Both gravity and magnetic anomalies of multi-sources added by 1% random noise（a） Gravity anomaly;（b） Magnetic anomaly.

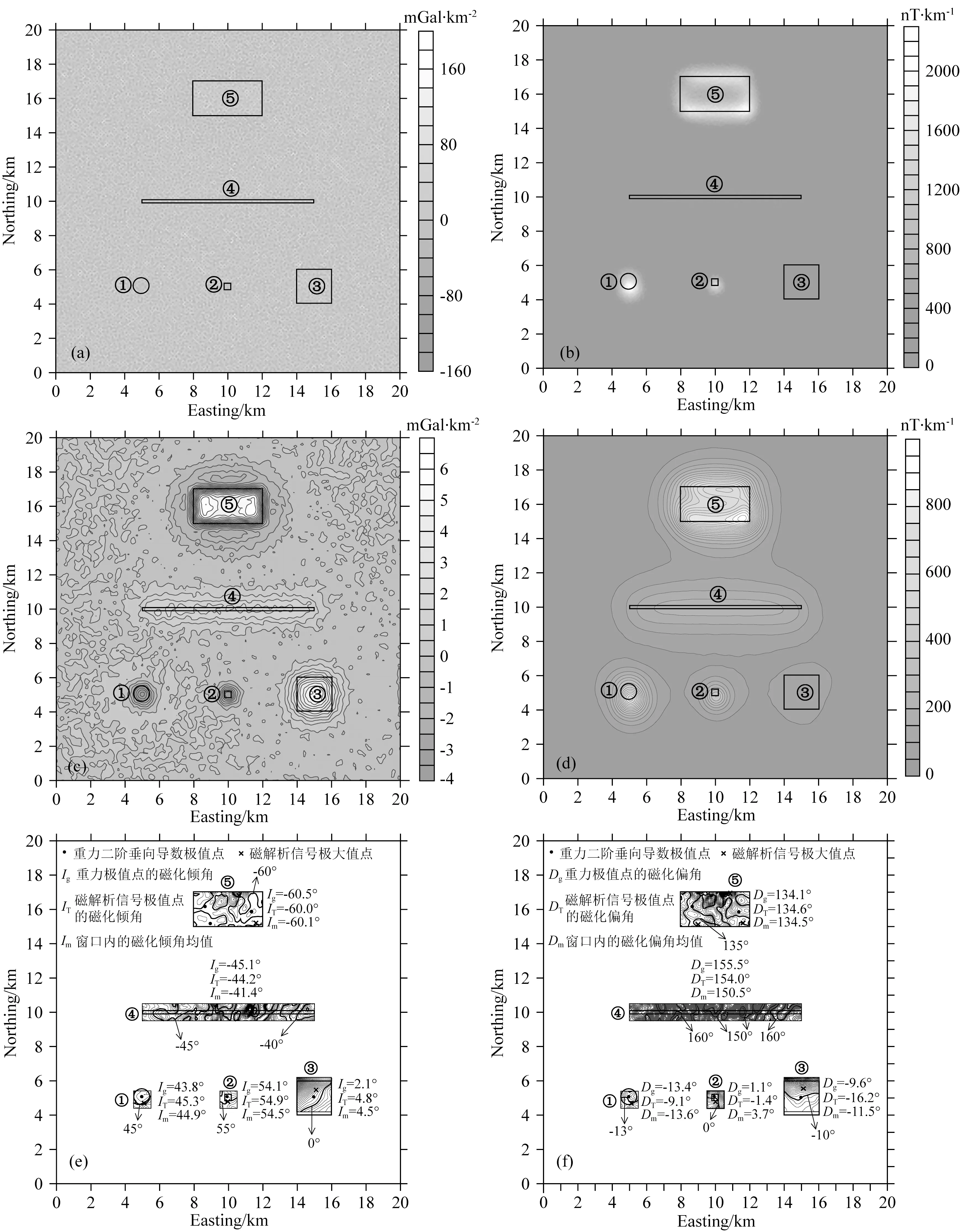
图7 含噪组合模型的磁化方向估计结果（a） 重力垂向二阶导数；（b） 磁解析信号；（c） 重力异常向上延拓0.5 km后的垂向二阶导数；（d） 磁异常向上延拓0.5 km后的解析信号；（e） 磁化倾角估计值；（f） 磁化偏角估计值.Fig.7 The estimated magnetization directions for the noisy gravity and magnetic anomalies of the multi-sources（a） The second vertical derivative of gravity anomaly;（b） The analytic signal of magnetic anomaly;（c） The second vertical derivative of gravity anomaly by upward continuation of 0.5 km;（d） The analytic signal of magnetic anomaly by upward continuation of 0.5 km;（e） The estimated magnetization inclination;（f） The estimated magnetization declination.

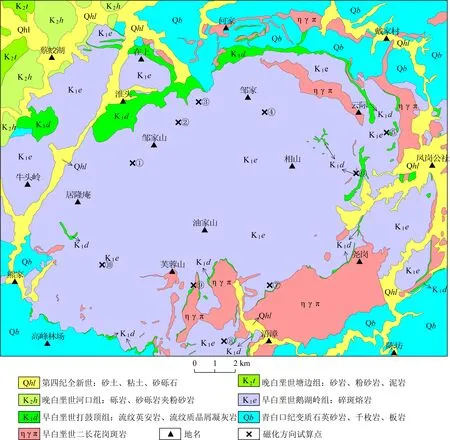
图9 江西相山铀矿田地质图（修自吴赞华，2015）Fig.9 Geological map of Xiangshan uranium orefield in Jiangxi Province （modified from Wu,2015）

3 实例应用

为了检验算法的实际资料应用效果，选取了江西相山铀矿田地区的地面1∶5万重、磁数据进行测试.江西相山火山盆地是我国第一大、世界第三大火山岩型铀矿田（Dahlkamp,2009）.相山火山盆地位于华夏板块湘桂赣地块北东缘乐安—抚州断隆带上，该区遭受了扬子—加里东期、海西—印支期造山作用，燕山期处于NEE向赣杭构造火山岩带西南端与近SN向赣中南花岗岩带的交接地带，发生了强烈的构造-岩浆-成矿作用（毛景文等，2011；郭福生等，2017）.相山铀矿田中心区域出露大面积的早白垩世鹅湖岭组碎斑熔岩，向外依次分布着条带状的早白垩世打鼓顶组流纹英安岩、早白垩世花岗斑岩及青白口纪变质岩，在西北侧还存在着晚白垩世的沉积岩（图9）.

为了了解哪类岩石具备重磁同源性，图10给出了相山火山盆地的主要岩石密度、磁化率散点图，可以看出，碎斑熔岩和花岗斑岩密度主要分布均在2.6～2.65 g·cm-3之间，均值均为2.64 g·cm-3，属于低密度体；流纹英安岩密度值主要分布在2.65～2.70 g·cm-3之间，均值为2.69 g·cm-3，为中高密度体；而变质岩密度主要分布在2.7～2.8 g·cm-3之间，均值为2.76 g·cm-3，为高密度体.碎斑熔岩磁化率一部分在10～100×10-6SI，属于低磁性，但仍有一部分分布在100～1000×10-6SI，相当于中强磁性；流纹英安岩磁化率同样是一部分在10～100×10-6SI，一部分在100～1000×10-6SI，还有少量部分大于1000×10-6SI，即流纹英安岩磁性变化较大，弱、中、强磁性均有存在；花岗斑岩磁化率大部分分布在10×10-6SI附近，少部分则位于100～1000×10-6SI，整体为弱磁性；变质岩的磁化率分布较为集中，主要在20～30×10-6SI之间，为弱磁性岩石.上述岩石密度、磁化率分析结果表明，变质岩为高密度弱磁性岩石，非重磁同源物质；花岗斑岩为低密度弱（中）磁性岩石，不建议做为重磁同源体；碎斑熔岩为低密度，弱与中强度磁性并存的物质，具有中强度磁性的碎斑熔岩则可认为是重磁同源型岩石；流纹英安岩为中高密度，弱、中与强磁性并存的岩石，具有中、强磁性岩石可作为重磁同源型物质.

图11a、b是相山铀矿田的1∶5万布格重力异常与总磁异常图，布格重力异常整体表现为中心重力低、外围重力高的异常特征，主要与大面积分布的低密度碎斑熔岩和高密度的变质岩有关.磁异常主要以局部异常为主，正磁异常主要分布在研究区的南侧与东侧，异常主要以SN、NE、NEE向为主，这些正磁异常在近正北侧都可以寻找到相对应的负磁异常分布；然而，在邹家山—邹家一带，存在大面积的负磁异常，且这些负磁异常幅值明显大于周围零星分布的正异常幅值，有可能该区域岩石存在与当代地磁场方向（地磁倾角和偏角分别为40.5°和-3°）不一致的剩磁.

为了寻找重磁同源位置，图12a、b给出了向上延拓500 m（1倍点距）后的重力二阶垂向导数和磁解析信号，并根据两者的极值关系选取了10个测算点，这些测算点都处于碎斑熔岩的分布区内，不过⑤—⑨号点附近都有流纹英安岩出露.利用3×3（1.5 km×1.5 km）窗口计算出了这10个测算点的磁化倾角与偏角，结果见表3.可以看出，①—④号点上的磁化倾角均为负值，且磁化偏角均位于东南向，基本与当代地磁场方向相反，由于这4个点是重力二阶垂向导数的极小值，且远离低密度的花岗岩，因此认为这些点的重磁同源体为低密度的碎斑熔岩.⑤—⑨号测算点上的磁化方向基本与现代地磁场方向一致，即认为这些点上的岩石磁异常主要是受现代地磁场感应而形成的，由于这5个测算点都是重力二阶垂向导数的极大值，故认为重磁源为流纹英安岩.⑩号点虽然磁化倾角也是正值，但明显小于地磁倾角，可能是碎斑熔岩和流纹英安岩综合反映的结果，不过该点位于重力二阶垂向导数的极大值处，认为流纹英安岩规模较大些.图12c、d给出向上延拓1 km（2倍点距）的重力二阶垂向导数和磁解析信号，并在图中选取了①、④、⑦、⑨这4个测算点进行磁化方向的估计，结果同见表3.可以看出，①和④号测算点上的磁化方向与现代地磁场方向基本相反，而其他2个测算点上的磁化方向与现代地磁场方向基本一致，反演结果与向上延拓500 m时重磁异常估计的磁化方向基本相一致，反映了磁法方向估计结果的可靠性.重、磁异常综合特征及磁化方向估计结果表明：（1） 碎斑熔岩之下可能广泛分布着流纹英安岩，尤其相山—云际—凤岗一带，地表零星分布的流纹英安岩可能在深部是连通的，而居隆庵地区的大量钻孔资料已揭示了这一现象（周玉龙等，2010；谢琛等，2018），这为相山铀矿田西部层间接触面部位寻找铀矿提供了参考；（2）碎斑熔岩具有强剩磁，且剩磁方向与现代地磁场方向基本相反，而流纹英安岩为顺磁性物质.

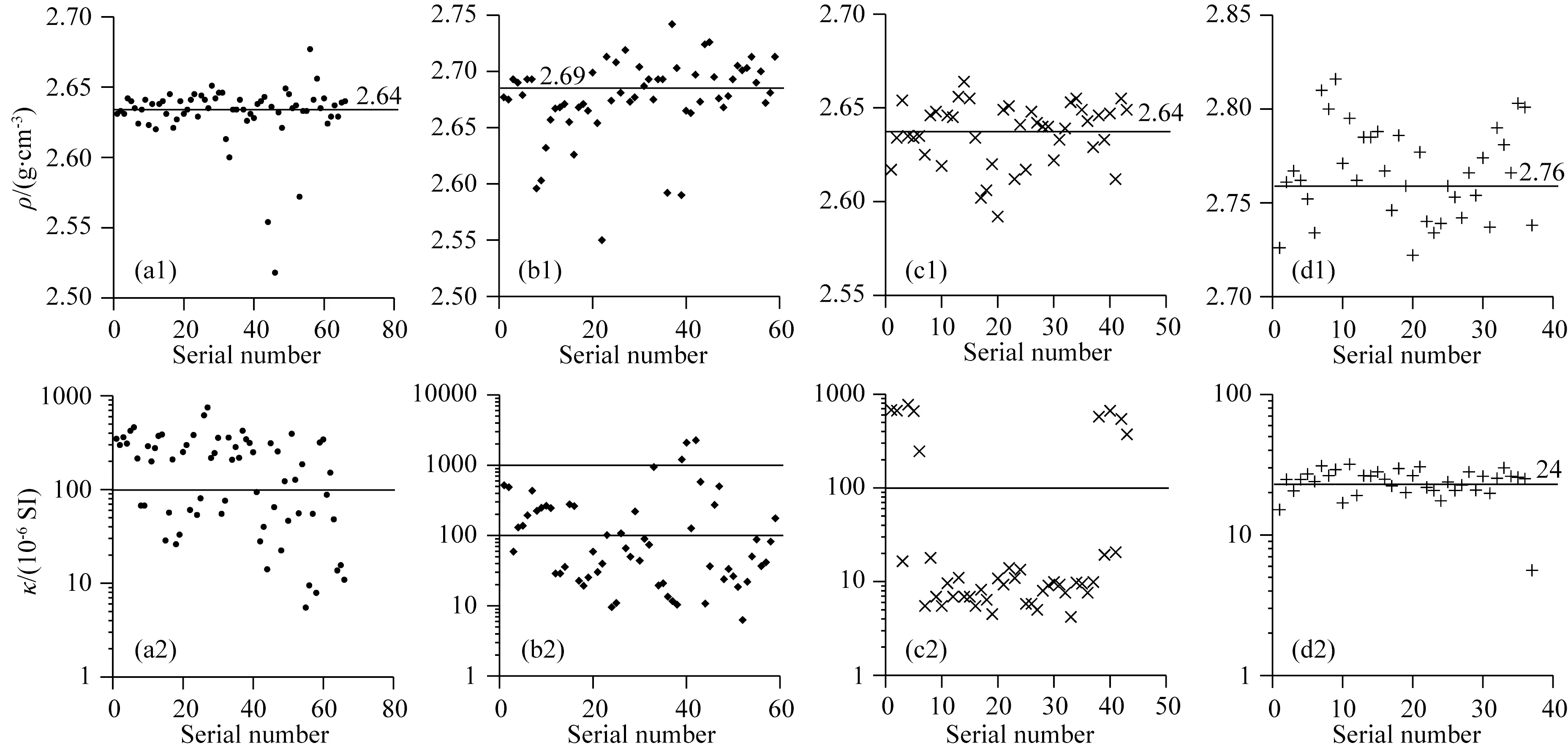
图10 相山地区主要岩石的密度、磁化率散点分布图（a1）、（b1）、（c1）、（d1） 碎斑熔岩、流纹英安岩、花岗斑岩及变质岩密度分布图；（a2）、（b2）、（c2）、（d2） 碎斑熔岩、流纹英安岩、花岗斑岩及变质岩磁化率分布图.Fig.10 Scatter diagrams of density and magnetic susceptibility of main rocks in Xiangshan uranium orefield（a1），（b1），（c1），（d1） Desity distributions of porphyroclastic lava,rhyodacite,granite porphyry and metamorphic rock;（a1），（b1），（c1），（d1） Magnetic susceptibility of porphyroclastic lava,rhyodacite,granite porphyry and metamorphic rock.

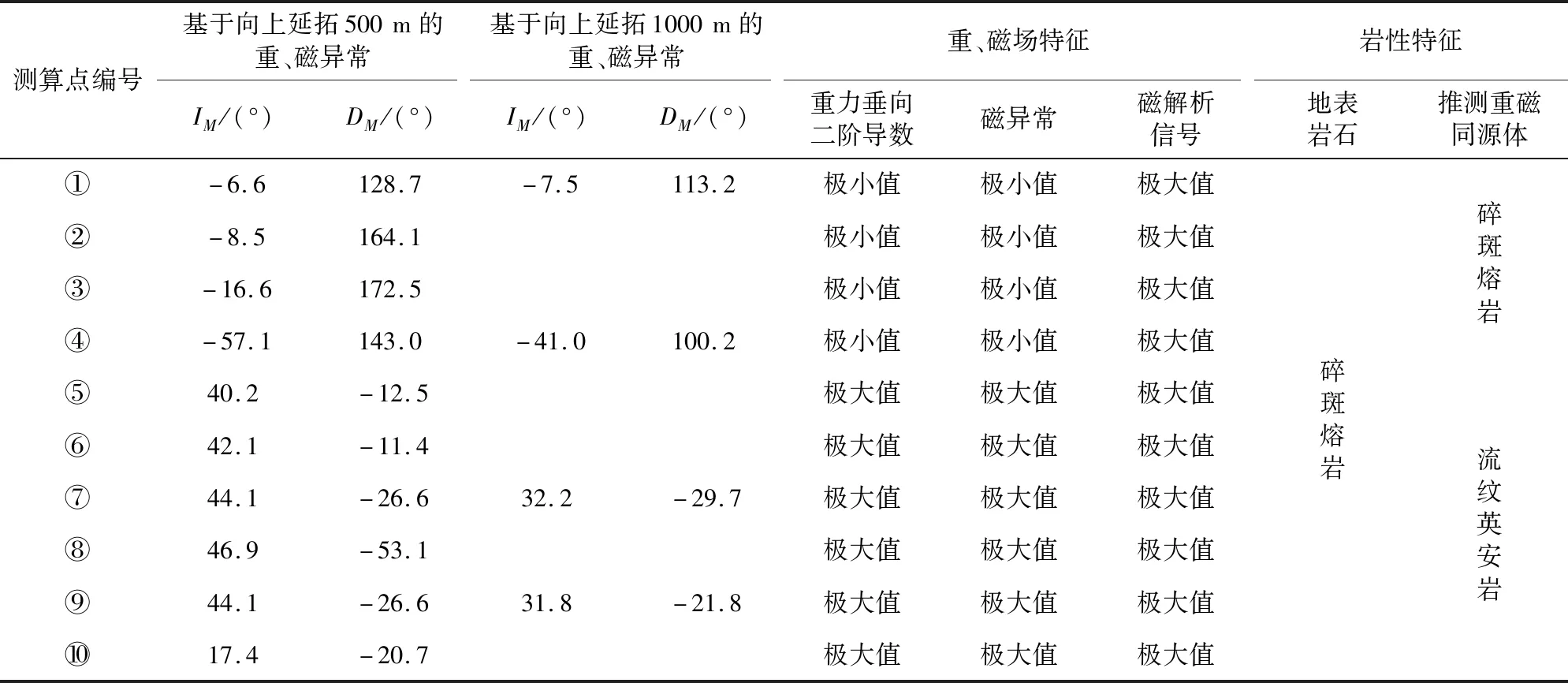
表3 相山铀矿田测算点的磁化方向估计结果Table 3 The estimated magnetization directions at different computing points of Xiangshan uranium orefield

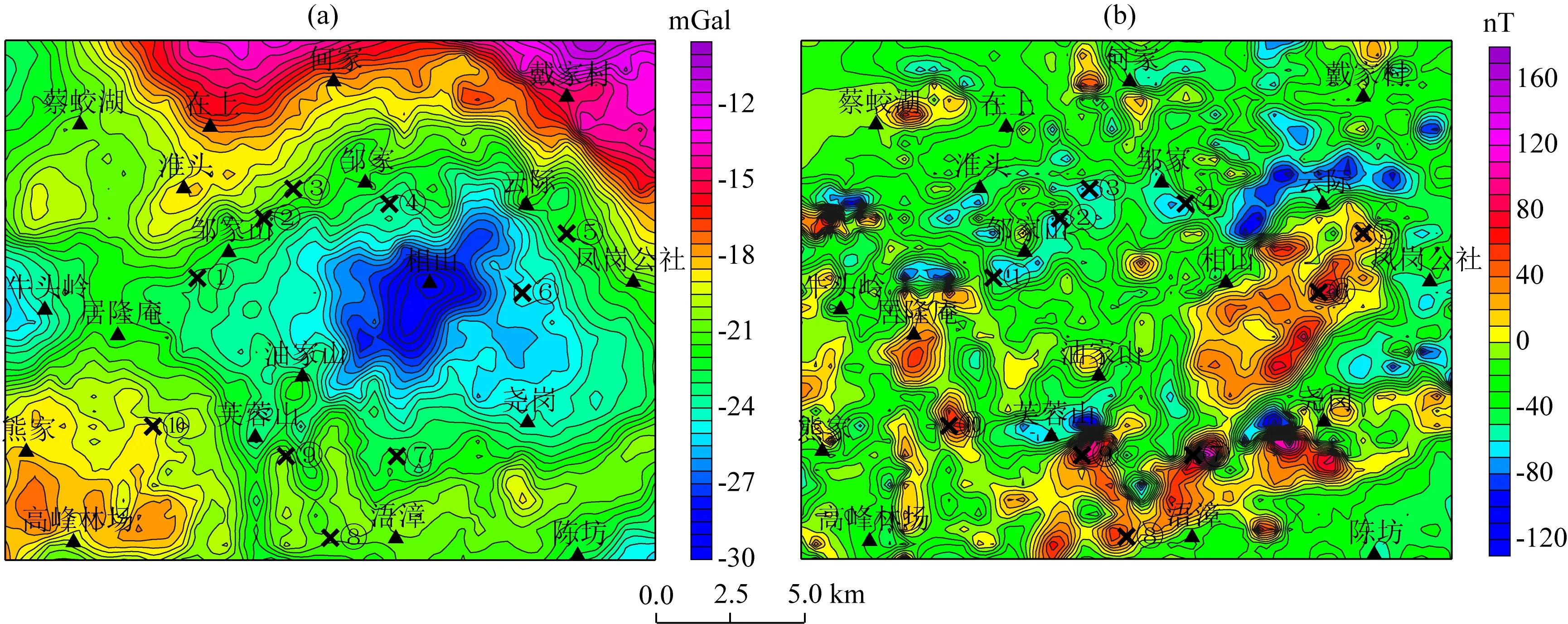
图11 相山铀矿田重磁异常（a） 布格重力异常；（b） 磁异常.Fig.11 Gravity and magnetic anomalies of Xiangshan uranium orefield（a） Bouguer gravity anomaly;（b） Magnetic anomaly.

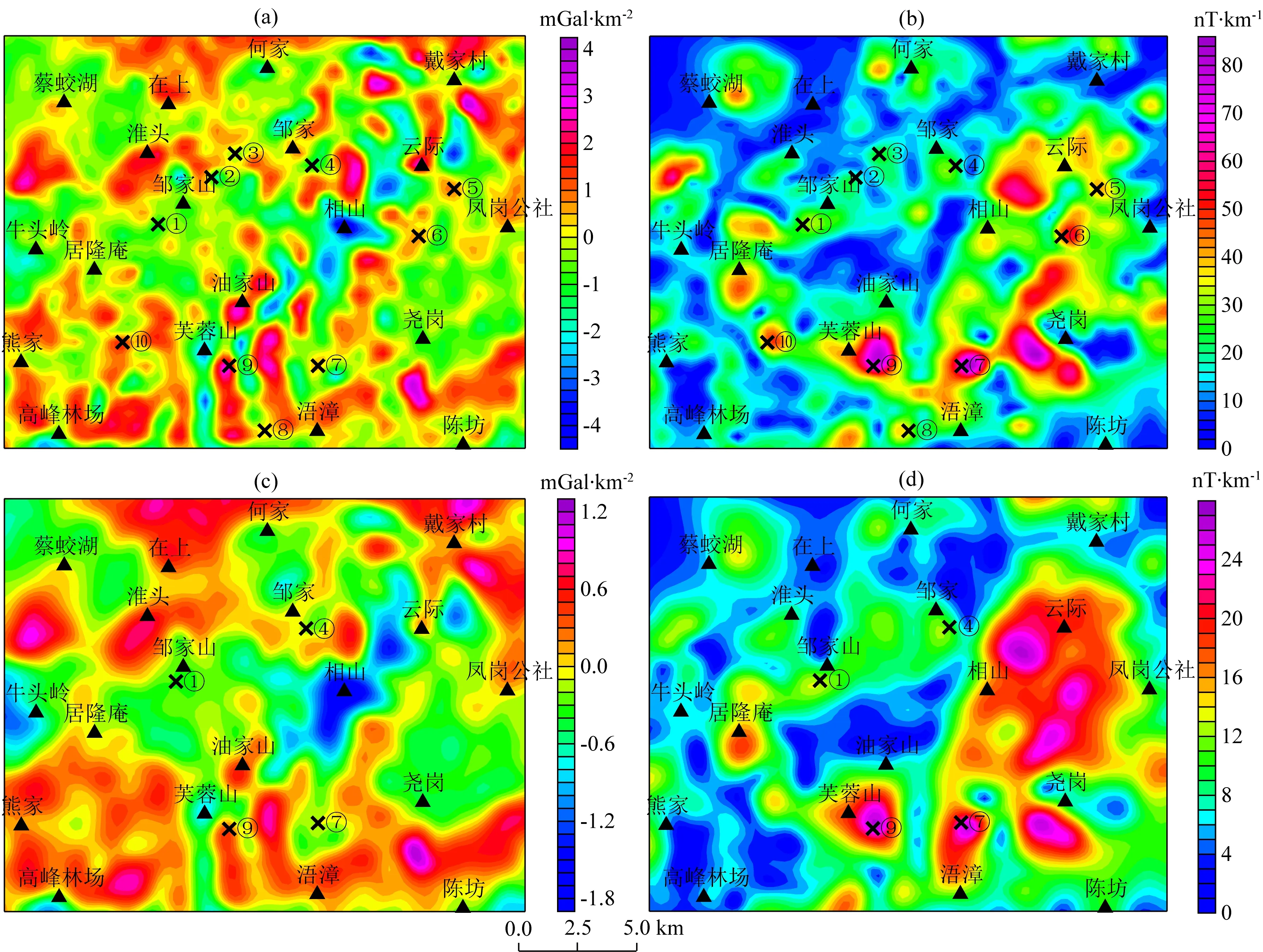
图12 相山铀矿田重、磁异常处理结果（a） 向上延拓500 m后的重力垂向二阶导数；（b） 向上延拓500 m后的磁异常解析信号；（c） 向上延拓1000 m后的重力垂向二阶导数；（d） 向上延拓1000 m后的磁异常解析信号.Fig.12 The processed results of gravity and magnetic anomaly over Xiangshan uranium orefield（a） The second vertical derivative of gravity anomaly by upward continuation of 500 m;（b） The analytic signal of magnetic anomaly by upward continuation of 500 m;（c） The second vertical derivative of gravity anomaly by upward continuation of 1000 m;（d） The analytic signal of magnetic anomaly by upward continuation of 1000 m.

4 结论与建议

从重磁泊松定理出发，推导出了磁异常一阶导数与重力位三阶导数及磁化强度的关系式，通过求解所构建的线性超定方程组，获取磁化强度的三个分量，进而得到了场源磁化倾角与偏角.从模型试验及实例应用结果中可得到以下认识：

（1）对于单一重磁同源体，本文方法在场源水平范围内外较大范围内都能获得准确的磁化方向.

（2）对于复杂的叠加场源，本文方法仍可以快速有效地获取各个场源的磁化倾角与磁化偏角，但反演精度受叠加异常影响而有所降低.

（3）当重磁异常含有较强噪声时，需要利用向上延拓来压制噪声干扰，提高反演解的稳定性和精度，但噪声干扰和延拓处理会降低磁化方向的估计精度，尤其对磁化偏角的影响较大.

（4）类似于Dannemiller和Li（2006）提出的互相关估算法，其优势是只需要单独的磁异常，但该方法在低纬度应用效果不理想，且对于同一数据体可能会产生多个磁化方向估计结果；本文方法相对这类方法而言，具有计算速度快和反演精度高的优点.

（5）在相山铀矿田重磁资料应用中，选择的10个测算点磁化方向反演结果表明，该地区的碎斑熔岩具有强剩磁，其下方广泛分布着顺磁性的流纹英安岩，这对该地区岩石磁学研究及铀矿找矿具有重要的参考价值.

由于本文方法建立在重磁泊松定理基础上，因此在重磁非同源体位置上是不适用的.在实际资料处理中要在充分分析地质情况与岩石物性（密度、磁化率）特征，结合重磁场及转换异常特征来判断引起重、磁异常的场源是否为同源.另外，在使用过程中有以下几点建议：

（1）当确定了重磁异常具有同源性的基础上，具体的反演位置建议选用重力二阶垂向导数极（小、大）值与磁解信号极大值重合位置或相距较近的地方.

（2）当重、磁异常较为复杂时，建议选择较小的计算窗口来减小不同场源异常的相互干扰.

（3）由于方法使用了重力二阶导数和磁一阶导数，因此对噪声具有一定的敏感性，建议使用一定点距的向上延拓来削弱噪声影响，一般延拓1～3倍点距即可.如果延拓点距过大，叠加异常影响严重，反演精度会有所降低.