水位降落时土坝坝体渗流特性的交互式有限元模型

臧育樱，田 淳，赵燕兵

(太原理工大学 水利科学与工程学院，太原 030024)

1 研究背景

土坝渗流和坝坡稳定性是影响土坝安全的关键问题。坝前水位降落造成坝体内渗流场随之发生改变，不同程度地影响坝内孔隙水压力分布，危害坝体稳定性，极易造成上游滑坡等重大灾害[1-3]。

坝坡稳定性分析常用方法有极限平衡法和有限元法。目前对库水位降落时坝坡稳定性分析多采用极限平衡法[4]，例如张大伟等[5]建立二维模型对库水位降落时上游坝坡稳定性进行分析，朱朋等[6]对三峡库区滑坡体水位降落过程进行计算，得出滑坡体安全系数随水位降落不断降低。但极限平衡法存在诸多弊端，例如需要假定滑裂面，无法模拟坝坡从局部破坏逐渐扩展以至贯通成滑裂面的渐进破坏过程等[7]。而有限元法则可较为真实地反映材料非线性本构关系，实现各种复杂边界条件的求解，其中强度折减法在推求安全稳定性系数方面应用广泛。常见的有限元分析软件ABAQUS、ANSYS无自带水位变动边界设置[8]，多应用于稳定渗流分析中，对非稳定渗流一般将库水位降落划分为缓降和骤降，仍按照稳定渗流的方式进行计算。对缓降认为坝内孔隙水压力随水位降落同步发生变化，对骤降则认为坝内孔隙水压力随水位降落不发生变化，这些都是对实际问题的一种假设，与实际情况不相符，例如刘博[9]按照缓降方式对比加固前、后的心墙坝内浸润线变化，Lane等[10]采用强度折减法确定水位缓降以及水位瞬时骤降这2种极端情况下的坝坡稳定性。目前水位降落过程中坝内各部位的变形和孔压分布规律的研究较少,故有必要对非稳定渗流开展瞬态有限元分析方法的研究。

2 计算原理

2.1 流固耦合计算原理

土坝上下游水位差产生的孔压以体积力的形式，通过透水介质作用于土体，改变坝内应力场。使坝内土体发生变形，改变土体孔隙比和渗透系数，造成渗流场变化，二者相互作用，相互影响。耦合模型矩阵形式为

(1)

式中：K为土体刚度矩阵(kN/m3)；Δδ为位移增量(m)；ΔF为由外荷载引起的节点荷载增量(kN/m2)；ΔFS为变化的渗流体积力引起的节点荷载增量(kN/m2)；k(σij)为变化的渗透系数(m/s)；σij为有效应力张量场(Pa)；H为水头(m)；f为渗流场水头分布函数。

2.2 强度折减法计算原理

在弹塑性土体材料计算中，通过不断增大的折减系数Fr，对土体材料的黏聚力c和内摩擦角φ进行折减(式(2))。通过使土体单元在原荷载作用下因c、φ减小而发生塑性破坏，形成完整的贯通破坏带。此时，对应的折减系数为边坡稳定安全系数。

(2)

式中：c和c′分别为折减前后土体的黏聚力(kPa)；φ和φ′为分别为折减前后土体的内摩擦角(°)；Fr为安全系数。

3 程序二次开发

3.1 水位变动边界设置

库水位降落的非稳定渗流场计算是以上游水位最高时的稳定渗流场为基础的。对土坝渗流应力耦合分析时，在坝体和坝基的表面应同时定义静水压力和设置孔压边界条件[11]。

在稳定渗流计算中，渗流场处于动态平衡过程，静水压力、孔隙水压力改变只与边界条件的变化相关，与时间无关，仅与垂向坐标y呈线性相关。

即静水压力荷载为

F=γw(h(0)-y) 。

(3)

孔隙水压力荷载为

U1=γw(h(0)-y) 。

(4)

在非稳定渗流计算中，上游水位是时间t的函数，设为h(t)，静水压力、孔隙水压力非线性变化，是时间t和垂向坐标y的函数，设为F(t,y)、U1(t,y)。

静水压力荷载为

(5)

孔隙水压力荷载为

U1=γw(h(t)-y) 。

(6)

式中：F为静水压力(kN/m2)；U1为孔隙水压力(kN/m2)；γw为水体重度(kN/m3)；h(0)为上游初始水位(m)；h(t)为上游t时刻水位(m)；y为垂向坐标变量(m)。

3.2 自动处理库水位下降参数插件程序的实现

由于ABAQUS中的LOAD模块仅能施加作用点固定的静态荷载，故本文采用Fortran和Python语言联合开发ABAQUS用户子程序，实现交互式的非线性动态荷载的施加。该用户子程序命名为UL插件程序，其可根据上游初始水位H、水位下降高度Δh和下降历时t等水位降落参数，并基于DLOAD荷载子程序接口和DISP边界子程序接口与LOAD模块进行实时对接，实现随时间和空间位置发生变化的静水压力和孔隙水压力的赋值功能。UL程序进行了人机交互的可视化界面处理，可与ABAQUS深度兼容，只需在ABAQUS中启用该程序，根据提示输入不同方案下的水位降落参数，实现特定库水位降落过程的渗流场和应力场的计算。

4 模型验证

应用上述模型，计算均质土坝水位降落过程中的渗流场和应力，分析坝体渗流特性和坝坡稳定性，并与理论分析和已有研究结论进行对照。

4.1 渗流场验证

选用模型坝高74 cm，坝顶宽度10 cm，坝底长306 cm，坝面坡比为1∶2，上游水位H1=60 cm，下游水位H2=0 cm的均质土坝作为算例，进行渗流场的模型验证，模型源于文献[12]。

4.1.1 稳定渗流对比结果

恒定库水位下，对渗透系数为0.001 7 cm/s的模型坝体分别采用数值模拟和水力学三段法计算坝内浸润线，计算结果对比如图1所示，模型计算浸润线逸出点高度为26.94 cm，水力学法计算值为25.67 cm，模型计算结果较水力学法高4.43%，两种方法计算所得浸润线位置基本一致，证明采用本文模型对坝体进行稳定渗流场计算可行。

图1 坝体稳定渗流浸润线对比

4.1.2 非稳定渗流对比结果

分别对渗透系数为0.001 7、0.000 2 cm/s的两种不同土质的坝体水位降落过程进行计算。随着库水位降落，坝体内浸润线随之降落并出现分水岭，分水岭凸点高程逐渐降低，与已有成果得到的水位降落下浸润线变化规律一致。陶同康[12]通过沙槽试验，刘洁等[13]、沙金煊[14]通过摄动法分别对各时段自由面分水岭凸点高程进行计算，同本文数值模拟计算结果对比见图2，各方法计算偏差见表1，说明模型对非稳定渗流场计算合理。

表1 浸润线凸点高程计算偏差表

图2 非稳定渗流浸润线凸点高程对比

4.2 应力场验证

模型选用坝高21.3 m，坝顶宽度7.3 m，基础底厚7.3 m，上游水位H1=17.1 m，下游水位H2=0 m，坝体、坝基采用同种材料的均质土坝[15]，示意图见图3。

图3 土坝示意图

计算上游水位自17.1 m降落至坝底过程中坝坡瞬态安全系数，0 h时刻坝体为17.1 m形成的稳定渗流，以位移-折减系数曲线出现明显拐点时为失稳条件。采用强度折减法分别计算水位下降0、85 h和90 h时的下游坝坡安全系数。分别同贾苍琴等[15]计算结果进行比较，见表2。本文计算结果同极限平衡法平均偏差为0.99%，同贾苍琴等有限元法平均偏差为4.85%，模型计算水位瞬态降落过程安全系数的方法较为合理。图4、图5分别为水位未发生降落时、水位降落85 h时刻滑动面对比。

表2 3种方法的安全系数比较

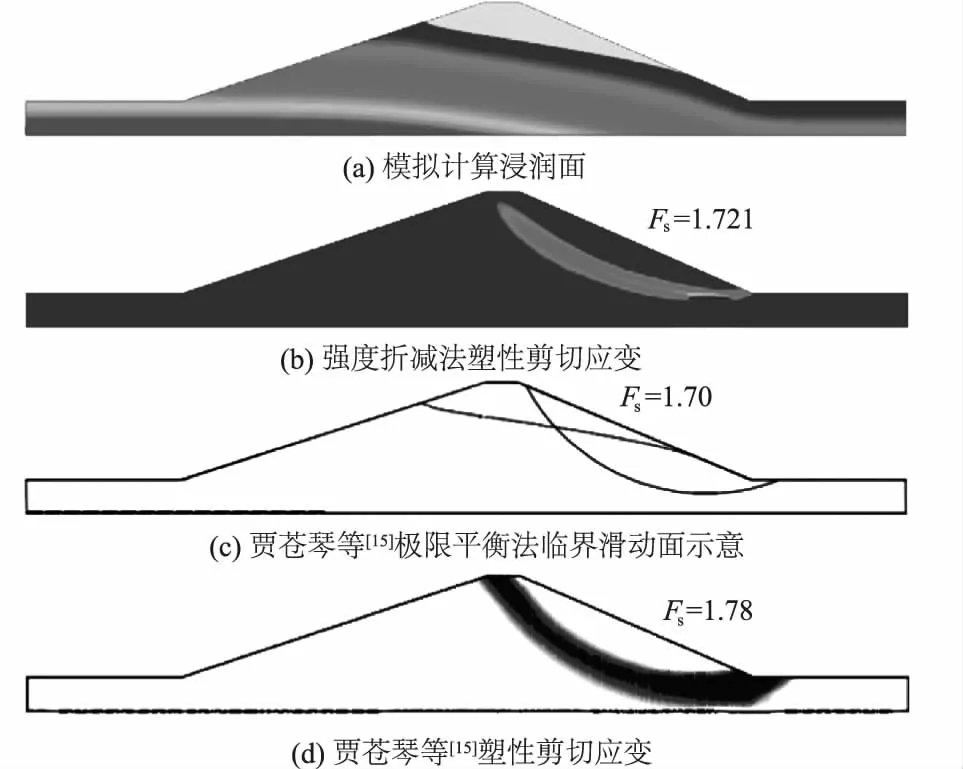
图4 水位未发生降落0 h时各方法计算的临界破坏机制对比

图5 水位下降85 h时各方法计算的临界破坏机制对比

5 工程算例

5.1 工程概况

十里河水库位于山西左云县西南，该坝为均质土坝，坝体全长为1 230 m，坝顶高程1 325.9 m，顶宽4 m，坝高16 m，上游坝坡1∶2.75。下游马道以上坝坡1∶2.25，马道以下坝坡1∶2.5。坝基上层为3 m厚的强透水的卵石混合土层，坝轴线上游马道附近碎石层中加设坡比为1的黏土截水槽。根据碾压土石坝规范，确定非常运行条件水位变动范围，自校核洪水位1 325.54 m降至死水位1 318.2 m。具体工程布置剖面见图6。

图6 十里河水库大坝横剖面图

5.2 模型设置

根据大坝剖面图，模型范围取坝体和坝基两部分。坝基深度取20 m，水平方向向上、下游各取约30 m，总长150 m，采用CPE4P四节点单元，网格总数15 877个，节点16 255个，如图7。坝基约束左右两侧水平位移，底部同时约束水平、竖向位移，上下游坝坡、河床和坝基两侧均为透水边界，坝基底部为不透水边界。模型整体施加重力荷载，上游坝坡施加非线性的静水压力荷载及孔隙水压力边界。模型分区中①为坝体素填土区；②为强透水的卵石混合土层；③为截水槽黏土层；④为坝基素填土层，具体材料参数见表3。

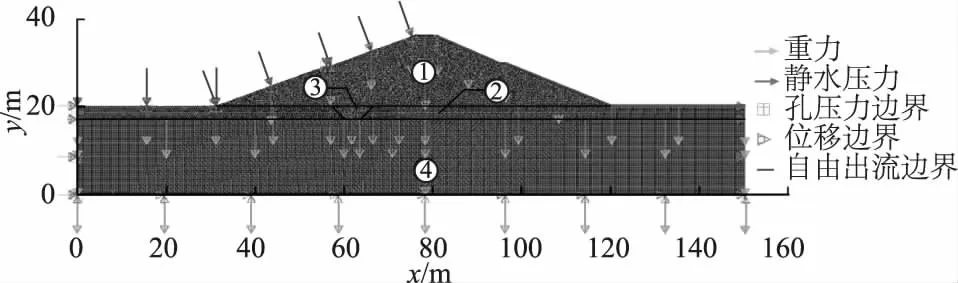
图7 十里河水库大坝模型设置及分区示意图

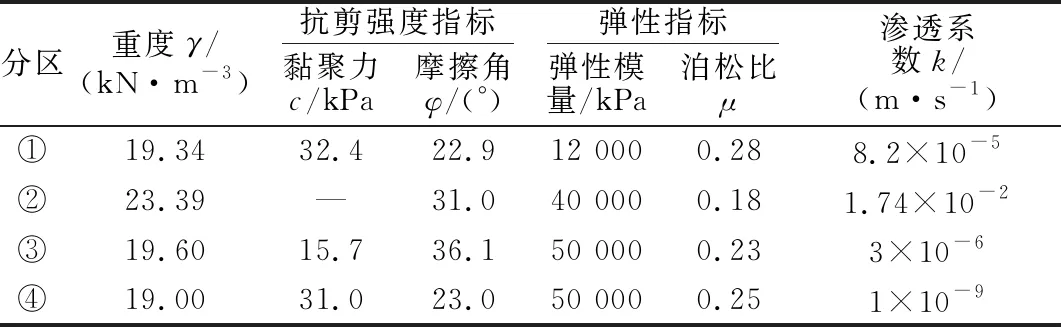
表3 材料参数

5.3 计算结果分析

5.3.1 浸润线分析

上游水位自1 325.54 m分别以速率0.05、0.10、0.50、1.00、1.50 m/d下降146.8、73.4、14.68、7.34、4.89 d至1 318.2 m，取初始时刻、水位降落完成时和水位每下降1.5 m(时间间隔分别为30、15、3、1.5、1 d)典型时刻浸润线，绘制成浸润线随时间变化图，见图8。水位下降过程中渗流场3个主要特征：①坝体中浸润线的下降同库水位下降相比，明显滞后。坝前水位下降速度越大，滞后现象越明显。②坝体上游临水侧浸润线呈凸形，出现分水岭且降速越大，浸润线上曲率越大。③浸润线最高点位置随着下降高度的增加向下游移动。这些特征均对上游坝坡不利，增大上游坝坡下滑的趋势。

图8 不同降水速率下坝体浸润线随时间变化

5.3.2 速度矢量分析

渗流场对坝体影响主要在上游部位，图9为上游水位以0.5 m/d速率下降至1 323.54、1 320.54、1 318.2 m时上游坝坡速率矢量图。在水位降落初期，坝体内孔隙水压力的消散速度与水位的降落速度相适应如图9(a)、图9(b)所示，表现为浸润面降落相比于库水位降落稍有滞后，仍为从上游流向下游。随库水位持续降低，浸润面滞后现象显著并产生分水岭，当水位降至1 320.54 m，如图9(c)所示。临水侧流场转变为靠近上游部分的水流朝向上游流动，而其余部分仍朝下游流动，当水位持续下降现象更为明显，如图9(d)所示。

图9 0.5 m/d降水速率下典型水位坝体流速矢量图

5.3.3 瞬时抗滑稳定性分析

上游水位分别以0.05、0.10、0.50、1.00、1.5 m/d速度下降时，上、下游坝坡的安全系数随上游水位变化关系如图10所示，降水完成时不同降速的上、下游坝坡安全系数见表4。

图10 不同降速下坝体上下游安全系数

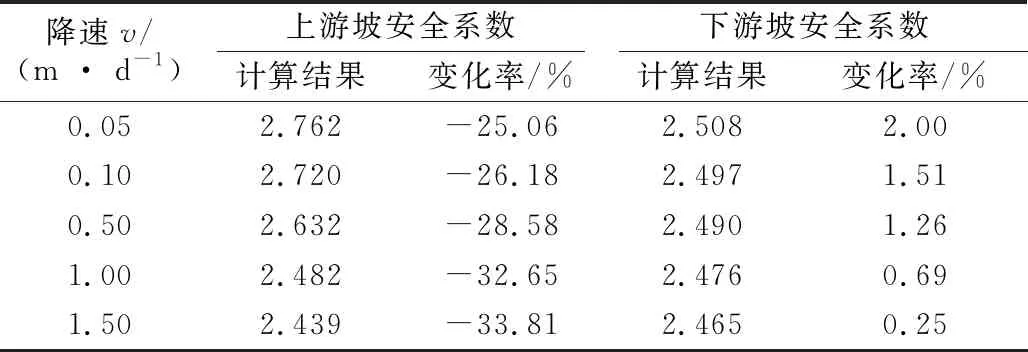
表4 降水完成时上、下游边坡安全系数

图10、表4表明：

(1)稳定渗流状态下，十里河水库大坝强透水层结合黏土截水槽的工程措施，能有效降低坝体内浸润线、逸出点高程，减少坝内渗径，加快坝内孔隙水压力的消散，增大下游坝坡安全系数，从而提高坝体的整体稳定性，使得下游坝坡安全系数受库水位降落影响不大。

(2)库水位降落完成时，下游坝坡安全系数稍有增大，上游坝坡安全系数持续减小且水位下降速度越大安全系数越低。库水位在1 325.54 m未降落时，上游坝坡安全系数为3.685，下游坝坡为2.459，降水完成后，上游坝坡安全系数降低率为30%左右，下游坝坡变化率仅为0.3%～2%左右，当降速为1.5 m/d时，上游坝坡安全系数降低率为33.81%，下游坝坡增加仅为0.25%。

(3)当上游水位降落4.5 m至H=1 321.04 m时，如图10虚线所示，水位下降速度越大，降落至同一位置时，上游坝坡安全系数越小。当降速为1.5 m/d时，此时上游坝坡安全系数为2.69，降速为0.05 m/d时，安全系数为3.009。

(4)水位降落初期，上游坝坡安全系数随水位下降速度的增加而大幅减小，随着降落时间的持续，安全系数变化幅度受水位下降速度的影响减小。

(5)在初始水位形成的稳定渗流情况下，坝体下游坡安全系数较小，较为危险。水位下降速度较小时，上游坝坡安全系数远大于下游坝坡，坝体的整体安全系数由下游坝坡决定。当水位下降速度增大，随降水历时的增加，坝体的整体安全系数逐渐转为由上游坝坡决定。如当以1.5 m/d降至1 318.6 m附近，上游坝坡安全系数小于下游坝坡，坝体整体稳定性由上游坝坡决定。

6 结 论

本文旨在结合算例探讨二次开发的库水位降落土坝模型的可靠性，并对水位降落瞬态过程中坝体渗流及稳定性进行分析，结果如下。

(1)借助Fortran语言编写UL子程序，Python 语言对UL子程序进行可视化处理，实现了交互式的非线性动态静水压力和孔隙水压力荷载的施加。

(2)利用二次开发模型，对坝体渗流和稳定性进行计算，对比理论分析和已有研究成果中浸润线位置、坝坡瞬态安全系数，结果均较为合理，验证了模型的可靠性。

(3)针对十里河水库大坝进行计算分析得出：①库水位降落时，浸润线降落较库水位降落存在滞后现象且出现分水岭，降落速度越大，浸润线降落的滞后现象越明显；②随水位降落历时的增加，临水侧流场自上游流向下游转变为靠近上游部分的水流朝向上游流动；③在降水初期，上游坡安全系数降幅随水位下降速度的增大而增大，随降水历时的增加，上游安全系数降幅受水位下降速度的影响减小。且降落至任意水位时，水位下降速度越大上游坝坡安全系数越低。水位自1 325.54 m降至1 318.2 m时，0.05 m/d降速时上游坡安全系数减小25.06%，1.5 m/d降速时减小33.81%。

(4)二次开发的UL子程序拓展了ABAQUS有限元法在非稳定渗流中的应用，可将其推广应用于各类降水工程中非稳定渗流场、应力场的计算。