周期函数的变换与最值问题的探究
广东省中山市桂山中学(528463) 蔡晓波
1.问题的提出
fn(x)=sin((4n+1)x),n ∈N 均在x=处取得最大值.
这个现象巧妙的地方在于:1.存在一个x值,使得无数个周期函数同时取得最值;2.fn(x),n≥1 实际上可以看成是由f0(x)伸缩变换得到.十分的巧妙,很好的体现了数学美.那么对于一般的周期函数满足怎样的变换规律才能使得多个周期函数在同一个x值取得最大值呢? 本文就如上问题展开讨论,与各位同行共勉.
2.相关结论
结论1函数f(x)为周期函数,最小正周期为T,且f(x)在(0,T] 内仅在a1,a2,a3,···,an取得最值,且0 结论2f(x)是最小正周期为T的周期函数且为奇函数,若f(x)在[0,T)内在x=a(0 证明下面仅证x=a为最大值的情况.设f(a)=M(M >0),则M为f(x) 最大值.由f(x) 为奇函数可得:f(−a)=−M,故f(−a)=f(T −a)=−M.由a ∈(0,T) 可得:T −a ∈(0,T).若在[0,T) 内存在x0使得f(x0)=−N <−M(N >0),则f(−x0)=N >M.故f(T −x0)=N >M与f(a)=M为最大值矛盾,即f(x)在x=T −a处取得最小值.x=a为最小值时,证明与上述过程类似,不再赘述. 根据结论1 和2,我们可以得出一些推论,在此之前我们先来看看几个引理: 引理1设数集A={x|x=k ∈Z},B={0,1,2,···,a −1},其中a,c ∈N+为常数且 互质;b为常数且b ∈B,则集合A包含的全部整数元素集合为{x|x=ak+p,k ∈Z,p为常数,且p ∈B},且当b取不同的值时对应的p不相同. 船舶靠离泊过程中的碰撞事故,可能是由于多种因素而导致的,这些因素类型多样,并且涵盖多方面内容,应当充分总结船舶靠离泊航行过程中的实践经验。船舶靠离泊航行过程中的安全事故的产生,很少是由单一因素所导致的,通常是由于多种因素的影响,多种过失链的积累,会对船舶靠离泊安全带来影响。船舶靠离泊航行安全事故的发生,基本上都与人为因素息息相关,而这些人为因素的产生,主要是由于相关人员责任意识的缺乏,专业技能较差,人员决策能力与指挥能力不足,以及航行经验与专业的不足等因素,这些因素都会对船舶靠离泊航行安全带来影响。 为证明该结论,我们先来看另一个引理. 引理2a,c ∈N+且互质,k ∈A={0,1,2,3,···,c −1},设ak除以c的余数为u,则当k取不同的值时,对应的余数u不相同;当k取遍集合A中的每个元素时,u组成的集合为A. 下面证明引理1: 下证当b取B中的不同元素时,对应的p不同. 设b1,b2∈B,b1b2且b=b1时集合A包含整数元素集合{x|x=ak+p1,k ∈Z,p1为常数,且p1∈B},上述证明过程中对应的M=M1,k′=k′1;b=b2时集合A包含整数元素集合{x|x=ak+p2,k ∈Z,p2为常数,且p2∈B},上述证明过程中对应的M=M2,k′=k′2. 综上所述:集合A包含的全部整数元素集合为{x|x=ak+p,k ∈Z,p为常数,且p ∈B},且当b取不同的值时对应的p不相同. 结合以上结论,我们可得如下推论: 推论1函数f(x) 为周期函数,最小正周期为T,且f(x) 在(0,T] 内仅在有限处取得最值,最大值为M,最小值为−M,则存在x0∈(0,T] 使得对于任意的n ∈N+,g(x)=|f(nx)|在x0处取得最大值M的充要条件是f(x)在x=0 处取得最值. 为了证明该结论,我们先来看看下边的引理. 引理3设数集A={x|x=,k ∈Z},若A包含无数个整数元素,则p,q必为有理数. 证明1.若p,q仅有一个为有理数,比如设p为有理数,q为无理数,且=m ∈Z,则q=为有理数,与q为无理数矛盾. 类似的可证得p为无理数,q为有理数也不成立,故p,q不可能仅有一个为有理数. 综上所述p,q必为有理数. 推论1 的证明充分性.因为f(x)在x=0 处取得最值,故|f(0)|=M(M为f(x) 最大值).因为f(x) 的最小正周期为T,故|f(nT)|=|f(0)|=M且|f(nx)|≤M,即g(x)=|f(nx)|≤M,所以当x0=T时g(x0)=g(T)=|f(nT)|=M. 必要性.根据推论1 的大前提,可设f(x) 在(0,T] 内仅在a1,a2,a3,···,am,m ∈N+取得最值,且0 根据{c1,c2,···,cm} ⊆{1,2,3,···,a −1},可得cja,结合引理1 可知集合A不包含形如a′k,k ∈Z 的整数,而集合A′又仅有有限个整数,故不存在x0∈(0,T]使得对于任意的n ∈N+,g(x)=|f(nx)|在x0处取得最大值M.故f(x)在x=T处必须是最值,即x=0 处为最值.显然,我们熟悉的余弦函数f(x)=cosx就是在x=0 处取得最值,且最大值为1,最小值为−1,故|cosnx|≤1,当x=0 时可让等号成立. 推论3若f(x) 是最小正周期为T的奇函数,当x0=(m,n为常数,m,n ∈N+,m 综上所述当u=nk+1或u=nk −1,k ∈Z 时,g(x)在x0或T −x0处取得最值.另外,根据推论3,我们可得如下推论: 设p=(m,n0为常数,m,n0∈N+,m≤且互质,n0≥ 2).根据推论3 可得:当u=n0k+1或u=n0k −1,k ∈Z 时,f(ux)在x0处取得最值.因为f(x) 即奇函数且最大值为M,故最小值为−M,故|f(ux)|≤M,当x=x0时,等号成立.又因为对于任意的n ∈N+,g(x)=|f((2n −1)x)|在x0处取得最大值M,故{u|u=2k+1,k ∈N}⊆{u|u=n0k+1或u=n0k −1,k ∈Z}.故3∈{u|u=n0k+1或u=n0k −1,k ∈Z}. 综上所述,n0=4. 上述的结论均是周期函数的变换与最值问题相关的结论,那么对于一般的周期函数的函数值与变换又有什么关系呢? 实际上,根据上述证明过程,我们不难发现可以将其推广到周期函数的一般函数值中去,且证明过程极其类似. 例如结论1 可以推广为: 结论3函数f(x) 为周期函数,最小正周期为T,且f(x) 在(0,T] 内仅在a1,a2,a3,···,an取得函数值m,且


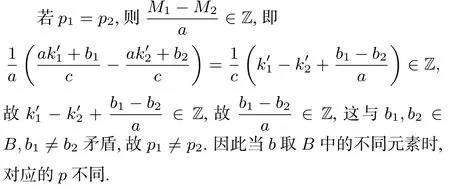









3.结论再拓展

4.回归教、学习题巩固



