不平衡网压下MMC⁃BESS的新型SOC均衡控制研究

贺坤，王灿，张坎，陈凯平，朱汉钦，符志宇，徐雷

（1.湖南长高高压开关有限公司，湖南 长沙 410200；2.长沙理工大学电气与信息工程学院，湖南 长沙 410114）

基于模块化多电平换流器（modular multilevel monverter，MMC）的高压柔性直流输电技术作为当代电压源换流器的新型直流输电技术，是当今柔性直流输电技术的研究重点。同传统直流输电技术相比，基于MMC的柔性直流输电技术具备独立调节有功与无功功率的能力[1-3]。但在其控制方面，子模块电容电压的均衡问题和各桥臂之间的环流问题一直是研究的重点[4-6]。

储能系统的加入，对于增加电网供电的可靠性和给予电网功率支撑方面起到了明显的作用。模块化多电平储能换流器目前已经引起国内外研究人员的关注[7-8]。由于储能电池的电压随电荷状态变化的影响很小，故在电池的正常工作状态可以视其电压恒定不变，储能子模块的电容电压就可以等效为电池电压[9]。故对于模块化多电平储能换流器，其避免造成储能容量配置浪费的子模块荷电状态的均衡控制成为研究的重点。现有许多文献都提出了子模块的荷电状态（state of charge，SOC）均衡控制，如通过控制相、桥臂、子模块功率的角度研究了三级SOC策略，实现SOC的均衡控制[10]。文献[11]建立电池组的非线性模型，采用模型预测方法得到SOC控制策略，但该方法控制复杂，参数难以整定。文献[12]分析了电源间的功率传输关系，提出了一种故障容错工况下的SOC均衡控制策略。

但对于不平衡网压状况下，上述方法都有所不足。不平衡网压工况下，相间功率不均衡和二次谐波对子模块SOC均衡的影响更为明显，过调制现象更加严重，进而影响SOC均衡速率和系统安全运行。基于以上，本文提出一种新型模块化多电平储能换流器功率均衡控制策略，该方法针对于相间，上、下桥臂间和子模块间提出两种不同的均衡控制策略，从而缩短均衡时间，避免能量配置上的浪费，防止过调制情况下对SOC均衡控制的影响。最后，通过仿真实验平台验证了所提方法的有效性和优越性。

1 MMC-BESS拓扑结构厔数学模型

MMC-BESS的拓扑结构如图1所示。图1中，vj和ij（j=a，b，c）分别为交流侧相电压和相电流；upj和unj分别为上、下桥臂的桥臂电压；ipj和inj分别为流经上、下桥臂的桥臂电流；Zs和Z0分别为交流侧等效阻抗和桥臂等效阻抗；udc为直流母线电压；icirj为j相环流；C为子模块电容；E代表与子模块电容并联的储能电池。由图1可以得知，若忽略电池SOC变化给电池电压造成的细微影响，MMC-BESS的子模块电容电压可以等效为电池电压，在理论分析中电池电压视为恒定值。

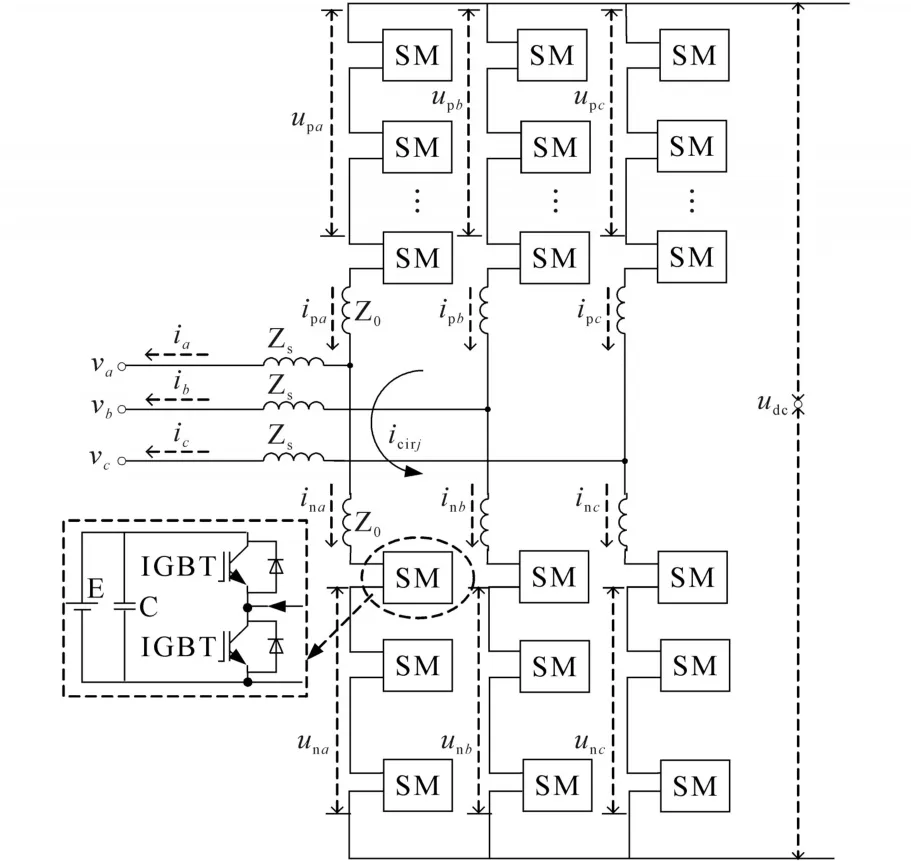
图1 MMC-BESS拓扑结构Fig.1 MMC-BESS topology

根据图1所定义的桥臂电流方向，桥臂电流可以表示为

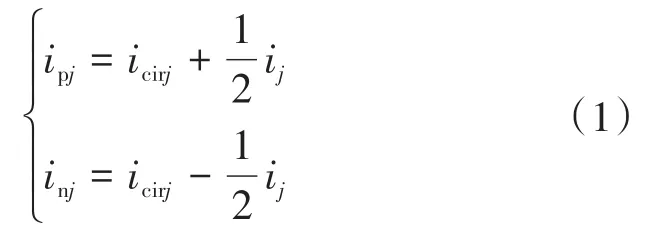
利用KVL可以建立MMC第j相电路方程：

将式（1）代入到式（2）中可以得到：

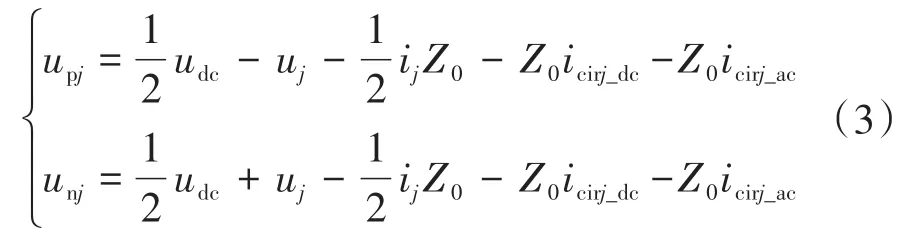
式中：icirj_ac为循环电流中的交流分量；icirj_dc为循环电流中的直流分量。

对于MMC-BESS系统来说，子模块电容电压的波动受储能电池充放电的影响很小。因此，在正常工况下，桥臂总输出电压可以看作是稳定的，不会出现以往传统MMC拓扑中提及的以二倍频为主的谐波电压分量。在三相参数完全相同的情况下，MMC-BESS内部直流侧电流由三相均分，交流侧相电流由上、下桥臂均分，桥臂电压中的谐波分量Z0icirj_ac应为0，桥臂电流的表达式可以修正为

式中：idc为直流侧电流。

因此，在正常工况下，环流中不包含二倍频谐波分量。环流表达式可以写为

对于储能电池而言，SOC的不均衡会降低系统的能源转换效率，造成资源配置的浪费。本文采用运用广泛的安时积分法对储能电池的SOC进行估计，该方法通过计算储能电池工作期间的充放电量来估算SOC，其定义表达式为

式中：S(t)为储能电池t时刻的SOC值；S(0)为储能电池初始时刻的SOC值；Q为储能电池的总电量。

式中：（it）为储能电池t时刻的充放电电流；Pm为储能电池的功率；um为储能子模块电容电压。

2 正常工况下常规SOC均衡控制策略

常规SOC均衡控制策略主要是以不同子模块电池SOC分布和各系统级的功率参考值为依据，对功率进行再分配，从而控制子模块电池的充放电流大小，从而达到SOC均衡的目的。

定义Ssum_avg为三相桥臂SOC总平均值；Sj_avg为j相桥臂的SOC平均值；Spj_avg和Snj_avg分别为j相上、下桥臂的SOC平均值，它们的表达式关系如下：

对式（6）求导可得：

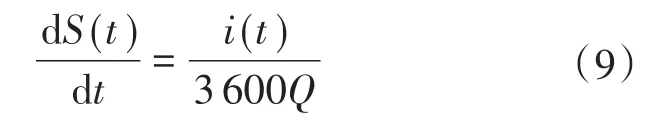
三相桥臂SOC总平均值Ssum_avg同j相桥臂的SOC平均值Sj_avg比较后，差值经比例放大得到j相桥臂子模块SOC均衡的均衡功率差值，结合式（7）和式（9）可以得到反馈值Sj_avg，同理可得桥臂间和子模块间的SOC均衡控制策略，整体的三级SOC均衡控制策略如图2所示，其中，Psum_avg为三相桥臂总功率平均值，Pj_avg为j相桥臂的功率平均值，为j相上、下桥臂第x个子模块电池的总荷电状态平均值，N为子模块个数。

图2 三级SOC均衡控制框图Fig.2 The block diagram of three-level SOC balanced control strategy

由图2可以发现，传统SOC均衡控制方法是依据SOC的差值变化量来调节子模块电池组间的功率分配，在发生不对称故障时，相间功率会发生突变，但SOC本身的变换是非常缓慢的，若此时继续用SOC平均值作为反馈量，系统子模块SOC达到平衡的时间将被拉长，造成资源上的浪费。因此，需要对不平衡网压下系统进行重新分析。

正常工况下，以整流端为例，忽略器件损耗，MMC-BESS在交流侧吸收的有功功率Pj_ac应该等于直流侧输出的有功功率Pj_dc，如下式所示：

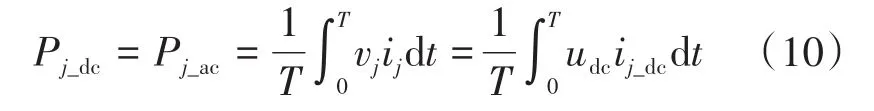
式中：T为周期时间；ij_dc为交流侧相电流中的直流分量。

根据能量守恒定理，即使在不对称故障下，交流侧吸收的有功功率依旧应该等同于直流侧输出的有功功率。但在网压不对称的工况下，交流侧相电压不平衡，因此交流侧相电流也会出现不平衡：

由式（11）所示，交流侧相电流的不均衡将导致MMC-BESS桥臂电流的不均衡，虽然子模块电容电压被稳定在电池工作电压，但各相间流经子模块的电流将出现差异。交流侧传输过来的二倍频功率脉动将进入直流侧，第x个子模块电容电压将会产生相应的二倍频纹波。根据瞬时功率理论，子模块瞬时功率表达式可以写为

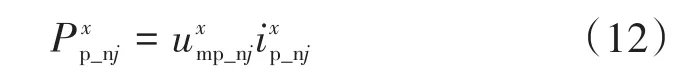
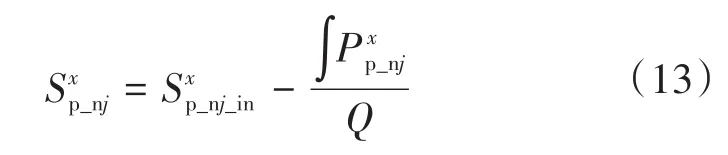
从式（12）中可以得到，子模块电池的荷电状态收到子模块瞬时功率的影响。由于在交流侧不平衡故障下，MMC-BESS系统三相交流功率不一致，储能电池在与交流侧进行能量交换后会将二倍频能量波动带到直流侧，MMC-BESS相与相间的传出功率不一致，将导致相与相间子模块电池SOC不一致。

由于电池组在工作条件和原始参数等方面存在差异，同一相上、下桥臂的等效电动势也可能有所差异，这是无法避免的。因此，在不平衡网压下，控制上、下桥臂子模块电池SOC均衡也非常重要。

3 新型SOC均衡控制策略

3.1 基于环流优化的相、桥臂间SOC均衡控制策略

MMC-BESS子模块拓扑结构如图1所示，根据荷电状态的定义，可以得到第x个子模块SOC与电池组流通电流表达式

根据能量平衡理论和式（12），交直流侧的功率应保持一致，对桥臂所有子模块输出功率进行叠加，可以得到：

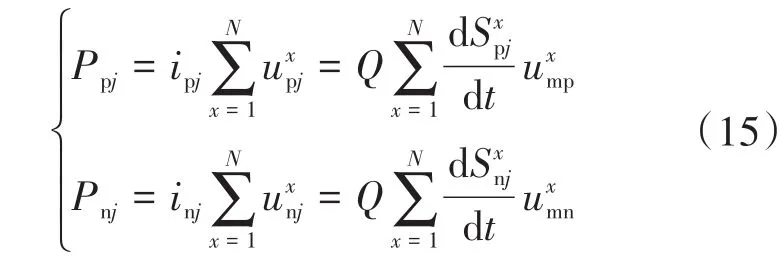
为控制子模块电池各个时刻的SOC均衡，将SOC平均值带入式（15）中，可以得到上桥臂的平均输出功率[13]：

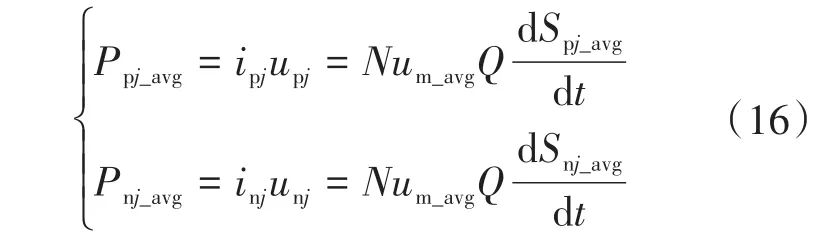
式中：下标“avg”为相应变量的平均值。

将式（1）和式（2）代入式（16）中可以得到单相总桥臂输出功率Psumj和单相上、下桥臂功率差Pp→n：

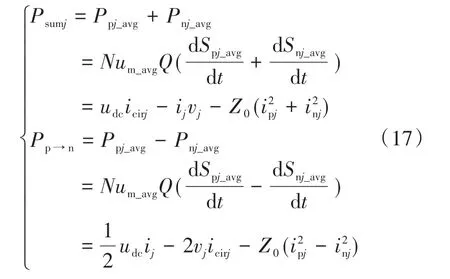
忽略式（17）中的交流分量，可以得到：

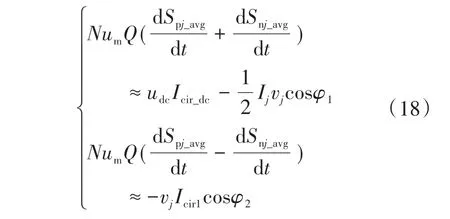
式中：φ1为变换器出口电压超前电网电压的相角；φ2为基频环流的相角；Icir_dc为环流的直流分量幅值；Icir1为环流的基频分量幅值。

由式（18）可知，环流中的直流分量可以控制相间子模块电池的SOC均衡，环流中的基频分量可以控制上下桥臂间子模块电池的SOC均衡。

在正常工况下，SOC的均衡控制通常采用相间SOC平均值（Spj_avg+Snj_avg）和上、下桥臂间SOC平均值（Spj_avg，Snj_avg）作为输入信号进行控制。但在不平衡网压下，三相功率出现偏差，故障相的SOC平均值会比较正常相偏差过大，此时若仍选择SOC平均值作为控制对象，控制时间将会过长，造成能源分配上的浪费。因此，针对于不平衡网压下的相间SOC均衡，本文采用各相总能量Wj作为反馈量实现相间SOC均衡。其中Wj的表达式为

为实现相间能量的均衡分配，各相的能量补偿量可以表示为

同时为应对不同控制目标下的输出功率变化，在相间SOC均衡控制中加入各相功率平均值Pj_avg的前馈环节。各相总能量Wj与三相总能量平均值Wj_avg比较后，输出经PI控制器后同各相功率平均值比较，输出得到各相功率参考值，参考值除以直流母线电压udc，最终得到在不平衡网压工况下的环流直流分量参考值。

相间SOC均衡控制框图如图3所示。

图3 相间SOC均衡控制框图Fig.3 Block diagram of phase-to-phase SOC balance control

在不对称故障下，受到交流电流中负序分量的影响，子模块电容电压会产生二次谐波电压分量，此时，上、下桥臂间的子模块电池组SOC变化会出现不一致，上、下桥臂的输出功率受到桥臂间SOC的影响，由上文可知，桥臂间的SOC均衡可以通过控制循环电流中的基频分量实现。设计上、下桥臂间的SOC均衡控制结构如图4所示，计算得到各相上、下桥臂的能量平均值Wp_nj_avg，与上、下桥臂能量Wpj和Wnj比较后，对MMC-BESS中的各相上下桥臂的输出功率平均值Ppj_avg和Pnj_avg进行求解，最后得到实现上、下桥臂间SOC均衡的环流基频分量参考值，其参考值的计算公式为

图4 桥臂间SOC均衡控制框图Fig.4 Block diagram of SOC balance control between bridge arms

式中：下标“ref”为相应变量的参考值。

3.2 基于判决函数的子模块间SOC均衡控制策略

不平衡网压下，子模块间的SOC均衡控制与正常工况下类似，但常规控制在调节过程中，子模块电压可能会超出输出范围、出现过调制的情况，此时系统中会产生大量谐波分量，谐波电压分量会影响子模块电压的均衡，进而造成影响SOC均衡控制的恶性循环。这种现象在不平衡网压下会更加明显，若此时不对SOC均衡控制增益进行调控，系统子模块SOC达到平衡的时间将被拉长。

因此，增益K3应该被限制为

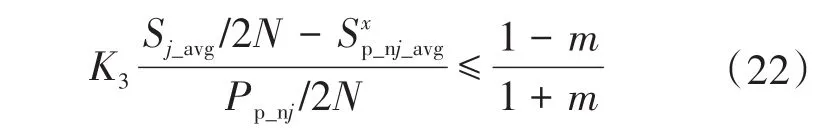
为进一步加快子模块间的SOC均衡控制速率，采用判决函数对SOC指令值进行再分类，子模块间的SOC均衡控制框图如图5所示，判决函数的分类流程示意图如图6所示。

图5 子模块间SOC均衡控制框图Fig.5 Block diagram of SOC balance control between SMs

图6 判决函数分类流程框图Fig.6 The flow block diagram of the judgment function classification

3.3 不平衡网压下桥臂能量波动抑制

正常工况下，MMC-BESS的子模块电容电压被稳定为电池电压，但当系统发生不对称故障时，交流电流中会产生影响功率均衡的负序分量。以抑制负序电流为目标，同时为抵御2倍频波动对子模块电容电压的影响，本文采用2倍频环流注入的方法，进一步降低不平衡网压工况下对MMC-BESS系统的冲击，所注入的2倍频环流参考值为

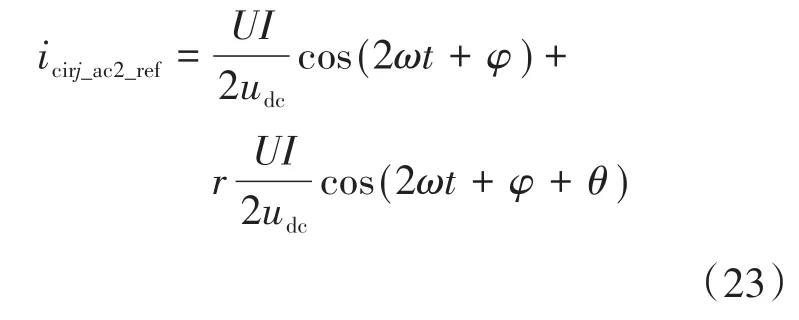
式中：U，I分别为三相交流电压、电流的幅值；ω为交流系统电压的角频率；θ为负序网压的相位；φ为交流侧相电流的相角；r为交流系统电压的不平衡度。

为实现系统相间SOC均衡、桥臂间SOC均衡以及2倍频波动抑制，最终得到的环流参考值可以表达为

式中：下标“1”，“2”分别为相应变量的 1，2 倍频变量。

综合以上，图7为系统总体控制框图，在该控制策略下能保证在不平衡网压下的正常运行，并且保持相间和桥臂间的SOC均衡。

图7 系统总体控制框图Fig.7 System overall control block diagram

4 实物验证

为验证在不平衡网压下，新型SOC均衡控制策略的可行性，配合传统SOC均衡控制策略进行对比实验，搭建了11电平的实验平台，平台照片如图8所示，平台具体参数如下所示：子模块个数N=10个，桥臂电感L=2.5 mH，桥臂电阻R=0.1 Ω，直流侧电压Udc=0.4 kV，子模块额定电容C=12 mF，负载电阻R=20 Ω，负载电感L=10 mH。在1 s时，B相电压跌落50%，并网侧三相电压波形vsj如图9所示。

图8 实验平台照片Fig.8 The photos of the experimental platform

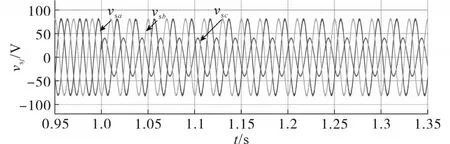
图9 并网侧三相电压波形图Fig.9 Three-phase voltage waveforms diagram on grid-connected side

图10为本文所提控制策略和传统控制策略两种均衡控制策略下的并网侧三相电流isj波形，通过观察可以发现，两种均衡控制都能使三相电流保持平稳，并且将幅值控制在合理范围内。但新型SOC均衡控制策略相比较传统控制策略而言平衡速度更快，并且纹波水平明显更小。

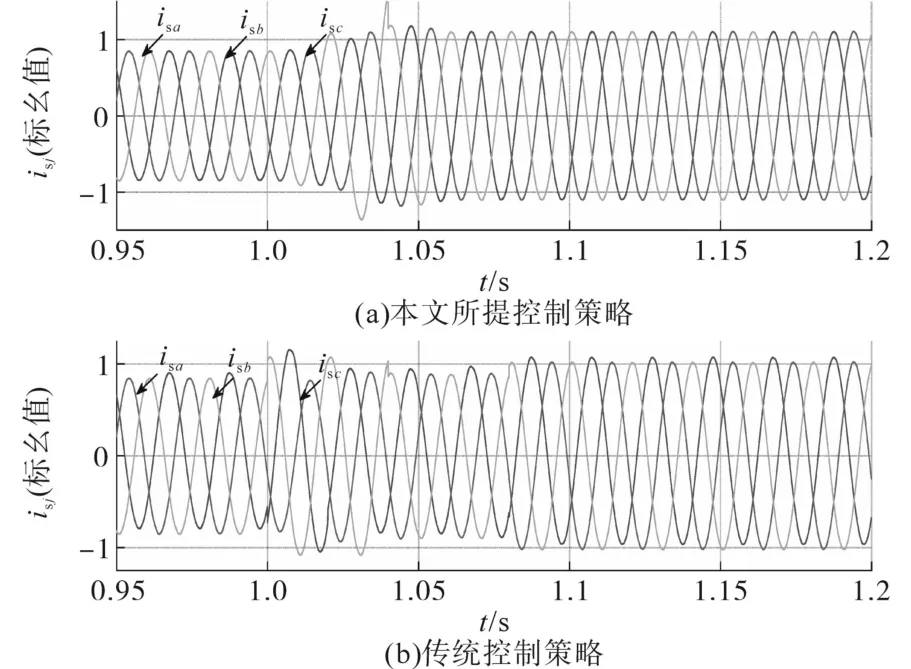
图10 并网侧三相电流波形图Fig.10 The waveforms of the grid-connected three-phase currents

图10中，1 s时，b相电压跌落，三相并网功率Pmj如图11所示。此时，SOC均衡控制策略启动，三相电池组的输出功率如图12所示。

图11 三相并网功率波形图Fig.11 The waveforms of the three-phase grid-connected powers

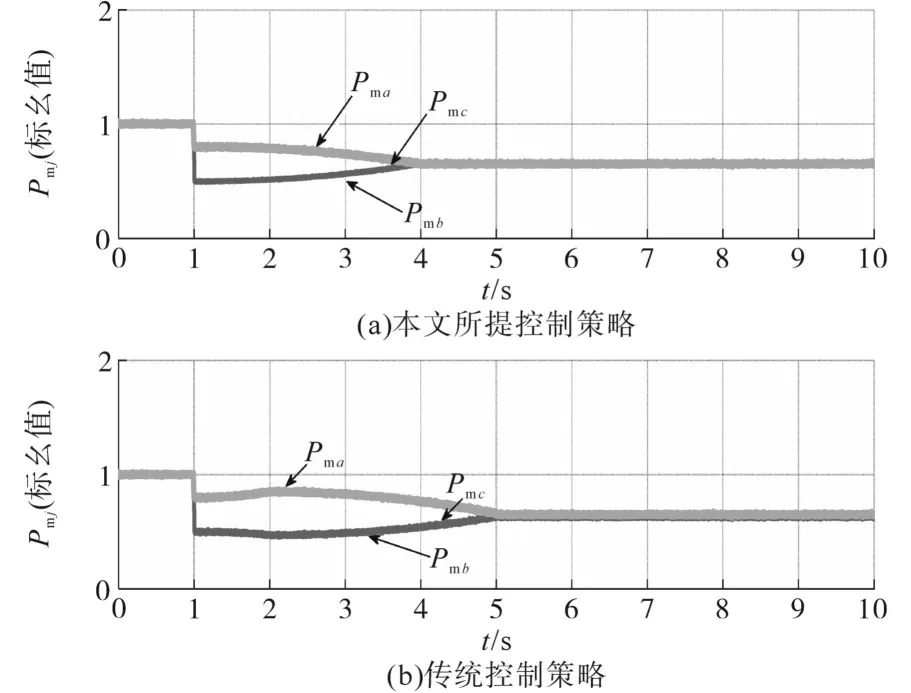
图12 三相电池组输出功率波形图Fig.12 Waveforms of three-phase battery pack′s output powers

由图12a可知，即使是在三相并网功率不一致的工况下，新型SOC均衡控制策略依旧能使得电池组输出功率趋于一致，并且相比较图12b中的传统控制策略来说，输出功率的平衡速度明显更快，这是由于本文所提控制策略跳过SOC估算环流，采用能量反馈量直接控制的结果。

两种控制策略在不对称故障下电池组SOC曲线如图13所示。

图13 电池组SOC曲线Fig.13 SOC curves of the battery pack

图13中，1 s时b相电压跌落，因此b相SOC值高于其他两相。在3.6 s左右，本文所提控制策略已经实现相间的SOC均衡，这跟三相电池组输出功率的结果基本一致。而在常规控制策略下，SOC的均衡时间较长，由于仿真平台的电压等级和电平数较小，若是在实际工程运用中，两种控制策略下SOC的均衡时间差将更长，这段时间造成的能源浪费不可小觑。

5 结论

1）通过对不对称故障下的MMC-BESS系统进行分析，计算其相间和桥臂间子模块SOC平均值公式，得到了桥臂环流中直流分量和基频分量与子模块SOC之间的关系，优化桥臂环流分量可以实现相间和桥臂间SOC的精准控制。

2）在不对称故障下，MMC-BESS系统相间输出功率出现不均衡，但SOC本身的变化率是缓慢的，因此无法实时反馈SOC平均值。若改用桥臂能量作为反馈量，在调控桥臂输出功率的同时，可以绕过SOC平均值对SOC均衡进行间接控制，其均衡速度大大加快，避免了SOC均衡过程中的能源浪费。对于子模块间的SOC均衡，在增益限制的基础上采用判决函数对调制信号重新调整，该方法可以避免过调制的发生，同时大大提高了SOC的收敛速率。

3）本文未考虑子模块电池组的健康状态（state of health，SOH）参数的影响，SOH的改变是否会对不对称故障下的SOC均衡造成影响，这也是后续研究需要考虑的内容。