全方位无线电力传输发射器的电磁结构设计

吕江平，李亚光

（1.上海电力大学电气工程学院，上海 200090；2.东北电力大学计算机学院，吉林 长春 132012）

无线电力传输技术（wireless powertransmis‐sion，WPT）作为一项突破性的技术在许多应用领域得到了广泛的关注，对传统的电力电缆传输技术的应用提出了挑战[1]。WPT将电能通过电磁场传递给负载，而电源和负载之间没有物理连接。这一特性使WPT能够为在恶劣环境下工作的设备提供高稳定性，如电动牙刷、电动剃须刀、自动水下航行器（autonomous underwater vehicles，AU⁃Vs）、植入式医疗设备[2]等。特别是WPT由于接收器的移动性，解决了可穿戴设备、助听器、移动设备等便携设备频繁充电的问题[3]。此外，还提出了各种方法来应用WPT为自动导向搬运车系统（automated guided vehicle system，AGVS）、电动汽车（electric vehicles，EVs）等大功率应用充电[4]。平面线圈结构简单、使用方便，在WPT系统中，收发结构是决定功率传输能力的关键。然而，它们以固定的方向产生磁通量，从而限制了接收机的自由定位和移动性。此外，当接收机偏离设计时，功率传输效率大大降低[5-6]。

早期针对全向WPT系统的研究提出了由两组方形线圈组成的发射机和由三个正交线圈组成的接收机[7-10]。这些发射机会产生一个旋转磁场，将磁通量扩展到二维（2D）。然而，这些结构有一个限制，他们是高度敏感的垂直失调的接收器。文献[11]提出了一种由三组方形线圈组成的发射机来实现真正的全向WPT。这个发射器产生一个三维（3D）磁场，这样接收器就可以在大范围内提供恒定的功率。文献[12]提出了一种碗状结构来实现均匀的全向磁场分布。发射机由缠绕在碗状表面的三个线圈组成。每个线圈中的电流大小被独立调制以产生一个三维磁场。虽然这些发射机产生2D或3D磁场，但电力传输只能在发射机内部进行。这大大减少了自由定位和灵活性。这些发射机通过控制线圈中电流的大小来自由改变磁场的方向，从而实现真正的全向WPT。接收机无论在什么位置都可以接收功率，从而最大限度地提高负载的移动性。然而，这类发射机的互感较小，导致功率传输距离较短、效率较低。为了提高全向WPT输电距离、提高效率，文献[13]提出了一种双三维发射机，发射机使用一个中间三维线圈来提高互感、提高传输效率。然而，中间的三维线圈会引起线圈之间额外的磁耦合，从而增加了系统的复杂性。文献[14]提出了交叉偶极线圈，以扩大功率传输范围，减少发射机体积，一个平面型交叉棒芯被用来最小化发射机的体积。由于铁心的高磁导率，变送器产生一个相对于匝数和线圈直径的强磁场。然而，旋转磁场虽然改善了自由定位和输电面积，但输电效率和输电距离低于平面线圈。另外，为了减小发射机的体积，去掉了z轴方向产生磁场的线圈，不能实现真正的全向WPT。因此，需要研究如何在不增加发射机体积和系统复杂性的前提下提高功率传输距离和效率。

基于此，本文提出了一种优化的磁结构，以提高全向WPT的电力传输效率，首先，分析了全向WPT系统的功率损耗，研究了影响系统效率的参数，在功率损耗分析的基础上，在不增加发射机体积和系统复杂度的情况下，采用了一种核心结构来提高效率。此外，本文提出了四种不同结构的候选核心结构来选择最优核心结构。利用有限元分析软件对各候选材料核心参数的互感进行了分析。为了进行公平的比较，计算每个核心结构的效率和体积，并利用这些值对候选结构的性能进行比较。采用多目标优化设计方法，从多种结构中选择最优磁结构。以效率和核心容量为目标变量，利用帕累托优化技术得到最优设计集。最后，给出了各种实验结果，验证了优化磁结构的有效性。

1 全向WPT系统设计

1.1 全方位无线电力传输电路概述

图1为传统全向WPT系统的示意图。

图1 传统全向WPT系统Fig.1 Conventional omni-directional WPT system

由图1可知，WPT系统主要由电压源、发射机和接收器组成。发射机是由三个互相正交的通电圆形线圈L1，L2和L3组成，且三个线圈公用一个圆心；接收器L4是由一个圆形线圈组成，其直径和匝数与发送线圈的直径和匝数相同，其位于发射机周围一定距离d的任意空间内。d为接收器线圈圆心与发射机线圈圆心的直线距离，即为输电距离；φ为极角，即d与发射器z轴的夹角；θ为方位角，即d在发射器xy平面上映射与x轴的夹角，故d，φ和θ共同决定了接收器的位置。C1，C2，C3和 C4为线圈上的串联补偿电容器；RL为负载电阻；I1，I2和I3为发射机电流；I4为接收器的电流。

图2为全向WPT系统的等效电路。

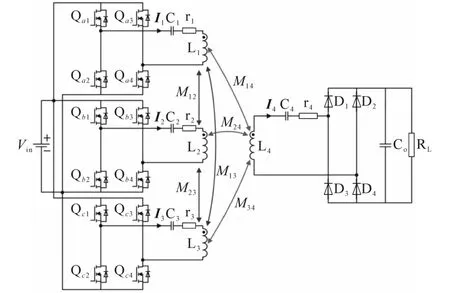
图2 全向WPT系统的等效电路Fig.2 Equivalent circuit of an omni-directional WPT system

由图2可知，该系统由三个发射电路和一个接收电路组成，发射电路与输入电压Vin并联，每个发射机电路由全桥逆变器、发射机线圈、寄生电阻和补偿电容组成，接收电路由补偿电容、接收线圈、寄生电阻、整流器和负载RL组成。Qn1～Qn4（n=a，b，c）为开关；r1～r4为等效寄生电阻；L1～L4为线圈的自感；D1～D4为整流二极管，Co为滤波电容。M12，M13，M23为发射线圈间的互感。M14，M24，M34分别为发射线圈和接收线圈之间的互感。当电流流过每个发射机线圈时，就会产生磁通密度。根据毕奥-萨伐尔定律[15]，发射机三线圈上的电流I1，I2和I3分别在发射机中心处产生磁通量密度B1，B2和B3，其计算公式如下：

合成的磁通密度Br为[16]

式中：R为线圈的半径；μ0为空气的渗透性；âx，ây，âz为笛卡尔坐标系中的单位向量；N为线圈的匝数。

因此，通过采用各种电流控制方法，全向WPT系统可以自由改变合成磁通密度Br的方向。在本文中，采用电流大小控制，使Br集中在接收器。发射机线圈电流的频率和相位是相同的。发射机线圈电流的大小调制方式如下：

式中：I为合成电流矢量的峰值幅值；Ii为Ii的峰值振幅，i=1，2，3。

1.2 系统功率损耗与效率分析

系统效率是输出功率与总功耗的比值。因此，要分析系统效率，首先要分析总损耗。系统的损耗由开关损耗PQ、补偿电容损耗PC、线圈损耗Pcoil、铁心损耗Pcore、整流损耗Prec、输出功率Po组成。开关损耗PQ由导通电阻rQ，cond上的功耗PQ，cond、开关损耗PQ，sw、死区损耗PDT组成。假设各开关器件的导通电阻相同，则PQ，cond的表达式为

式中：下标“rms”为相关变量的有效值。

为了减少PQ,cond，应选择rQ，cond较低的开关。移相控制时，开关电压为输入电压Vin，开关电流为Iicos（αi∕2），其中αi为相移角。利用开关电压和电流，计算PQ，sw为

式中：tOFF，tON分别为关断、开通时间；fs为开关频率。

PQ,sw与开关频率成正比，因此，降低开关频率会降低PQ,sw。

死区损耗PDT包括二极管导通损耗和反向恢复损耗：

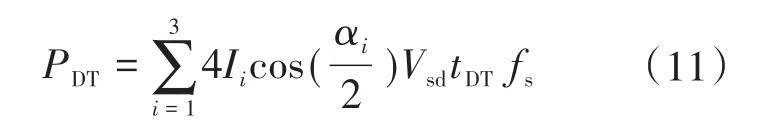
式中：Vsd为恢复电压；tDT为死区时间。

PDT与Vsd，tDT及fs成正比，因此，减少这些因素会降低PDT。

补偿电容损耗Pc为

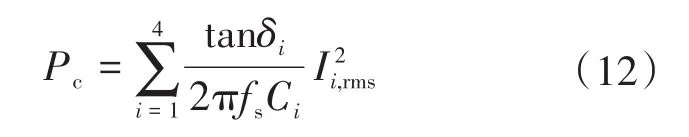
式中：δi为相角；tanδi为损耗因子。

低损耗因子的电容器可以减少Pc的损耗；Pc与开关频率成反比。

全向WPT在高频率下工作，环形并联线圈的Pcoil,cond计算方法为

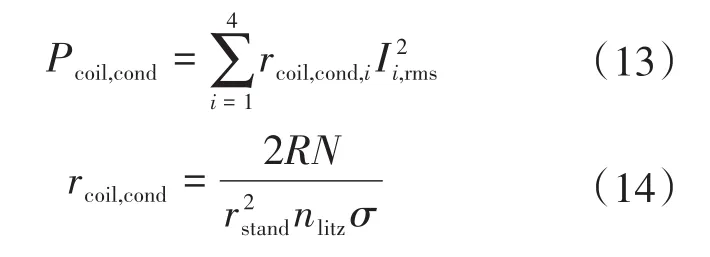
式中：rcoil,cond为各线圈的传导电阻；rstand为磁链的半径；nlitz为利茨线的股数；σ为铜的电导率。

临近效应Pcoil,prox的损耗是由相邻导体产生的磁场引起的：

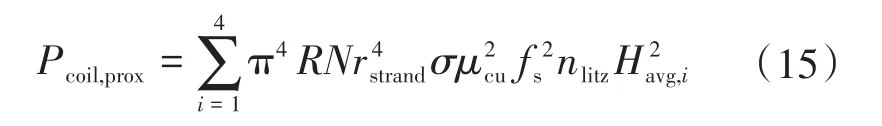
式中：μcu为铜的磁导率；Havg为导线横截面的平均磁场强度，为了准确分析，用有限元分析软件代替数学模型来估计Havg。

全向WPT系统在谐振频率附近工作。因此，线圈中的电流是正弦的，它产生一个正弦磁场。对于正弦磁场，利用Steinmetz方程可估计铁心损耗Pcore：

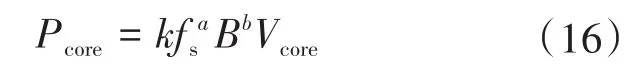
式中：B为磁感应强度峰值幅值；Vcore为内核的体积；k，a，b为核心材料的斯坦梅茨系数。

Pcore随开关频率的降低而减小。

根据图2由基尔霍夫电压定律可得：

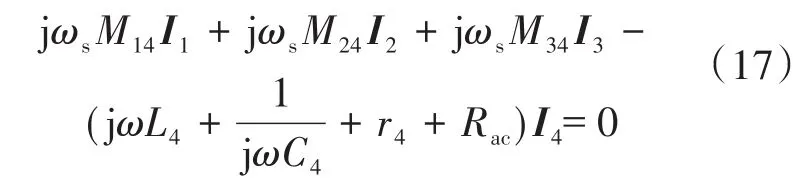
式中：ωs，ω分别为截止频率和角频率；Rac为等效交流电阻。

当全向WPT系统工作在谐振频率时，可得：

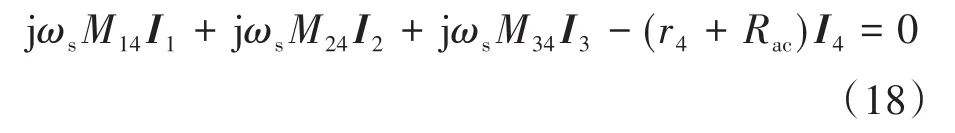
结合式（5）～式（7）及式（18），得到I4和I4，rms为

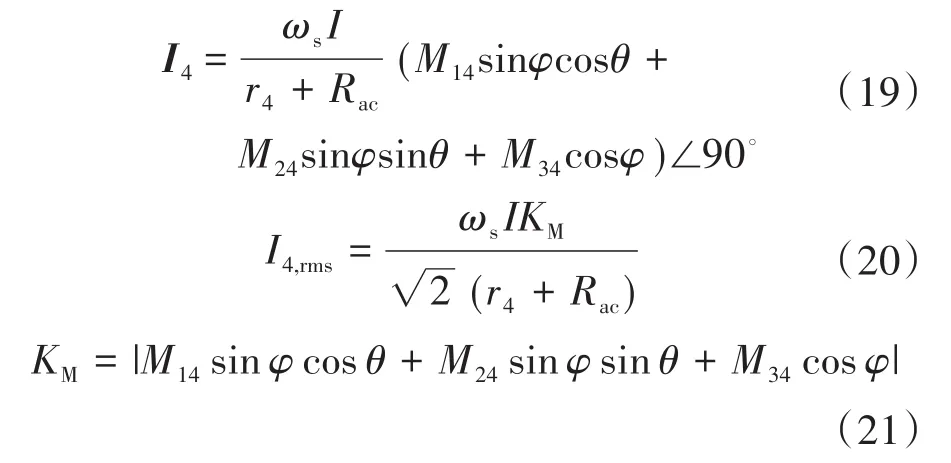
式中：KM为发射机与接收机之间的互感因子。

整流器损耗Prec可表示为

式中：Vth为二极管的阈值电压；rD为二极管的寄生电阻。

为了降低Prec，应选择低Vth和低rD的二极管。

输出功率Po可表示为

如果发射电流的大小是固定的，Po取决于角频率和互感因子。

系统效率η计算为

为了提高效率，应增加Po，同时减少功率损耗。

随着频率的增加，Po增加，而PQ,sw，PDT，Pcoil,cond，Pcoil,prox和Pcore同时增加。因此，高的工作频率并不能保证效率的提高。另外，由于开关频率影响系统的功率密度和质量因数，所以开关频率的选择非常复杂。如果开关频率固定，则PQ,cond，PQ,sw，PDT，Pcoil,prox，PC,1-PC,3和Pcoil,cond,1-Pcoil,cond,3均为常数。则系统效率变为

I4,rms与KM成正比，因此，当KM增加时，Po，PC,4，Pcoil,cond,4和Prec也增大。由于rC,4和rcoil,cond,4一般比Rac小得多，系统效率可近似为

如果未使用铁心，则Pcore=0。Vth造成的损耗与KM成正比，Po与KM的平方成正比；因此，提高KM可以获得更高的效率。另一方面，如果将铁心添加到发射机中，提高KM并不能保证获得高效率。

因此，为了实现高效率，需要设计一种既考虑KM又考虑Pcore的磁结构。

2 磁结构优化设计

2.1 候选磁结构分析

为了提高KM，发射器和接收器之间的互感应该增加。如果电力传输距离是固定的，互感由发射机的几何形状决定[17-20]。虽然增加线圈的匝数和直径是提高互感的一种简单方法，但它增加了变送器的体积。本文在变送器内部插入铁心，在不增加变送器体积的情况下提高了互感。铁心具有较高的相对磁导率，集中发射机产生的磁通量。因此，发射机中心处产生的磁通量密度Br增强，通过接收线圈的相互磁通量增加。但在这种情况下，由于Pcore的存在，高KM并不能保证高效率。本文候选磁结构如图3所示，它们出自文献[3-11]中的经典磁结构。

由图3可知，磁结构在xy，yz和zx平面上均对称。由于约束条件，大多数多面体都有非常多的面，且类似于一个球形磁芯。立方体核是面数最少的多面体。因此，球形核和立方体核代表多面体。交叉的棒磁芯和三正交的平面磁芯分别代表棒磁芯和板磁芯组成的磁性结构。球形铁心的几何形状与发射机线圈的几何形状相似，如图3a所示。Rsp为磁芯半径。球形磁芯是唯一一种可以完全占据发射机体积的结构。立方体磁芯如图3b所示。lcu为立方体磁芯的边长。由于立方体核的截面是正方形的，所以它所能占据的最大体积比球形磁芯要小。交叉钢筋磁芯由三个钢筋铁心组成，如图3c所示，其中，lcb和Wcb分别表示棒材芯的长度和宽度。虽然交叉的棒芯占有较小的体积，但每个棒芯都位于发射机的x-，y-和z-轴上，以引导磁通量到所需的路径。三正交平面磁芯由三个圆形磁芯组成，如图3d所示。Dtp和Htp分别为圆形核的直径和高度。三正交平面磁芯具有球面磁芯和交叉钢筋磁芯相结合的优点。由于这个磁芯的几何形状类似于发射机线圈，它可以占据一个很大的体积。此外，每个圆线圈位于xy，yz和zx平面。线圈R=75 mm，N=16。在有限元软件中，将多圈线圈建模为一个具有等效截面面积的体积线圈。磁芯材料为PM-12，相对磁导率为3 200。等效半径Rs=65 mm，lcu=90 mm，lcb=130 mm，Wcb=10 mm，Dtp=130 mm，Htp=10 mm。利用有限元软件对上述磁结构进行了建模及磁通密度分析。图4为Il=4 A及I2=I3=0时磁感应强度的仿真结果。

图3 候选磁结构Fig.3 Magnetic structure candidates

图4中，励磁电流的总安匝设为64 A，箭头表示磁通量密度Br的方向，颜色表示Br的大小。球形磁芯占据发射机内部大部分空间，使磁通密度沿x轴方向对齐，如图4a所示。yz平面内的磁通密度表明，球形磁芯发射机的磁通密度整体增强。特别是，球形磁芯非常靠近发射机线圈，大大增强了发射机线圈附近的磁通密度。图4b为带有立方磁芯的变送器的磁通密度。与球形磁芯一样，立方磁芯使磁通密度沿x轴方向排列。然而，立方体磁芯的几何形状与发射机的几何形状不同；因此，一些磁通量路径不能被引导到期望的方向。yz平面的磁通密度明显高于球形核的磁通密度。这是因为立方体磁芯的截面积小于球形磁芯的截面积。由于立方体磁芯的截面为正方形，因此发送线圈周围的磁通密度不会增强。图4c所示为带有交叉棒磁芯的发射机的磁通密度。与球形或立方体磁芯不同，交叉钢筋磁芯体积小；因此，大部分磁通不能被引导到期望的方向。但是，由于三个棒芯位于合成磁通密度Br的基向量B1，B2，B3的方向，因此，x，y，z轴附近的磁通密度大大增强。从yz平面的磁通密度可以看出，发射机中心附近的磁通密度非常高。但总体磁感应强度并未增强。三正交平面磁芯的发射机的磁通密度如图4d所示。与交叉棒磁芯相似，三个平面磁芯位于xy，yz，zx三个平面，引导每个平面附近的磁通量向B1，B2，B3移动，因此，在y轴和z轴附近的磁通密度增强，从yz平面上的磁通密度可以看出。此外，这个磁芯的几何形状与发射机相似。因此，发射机线圈附近的磁通密度要高于交叉的磁芯。利用有限元分析软件对M14～M34进行了估算。输电距离为150 mm时，随着磁芯参数的增加，磁芯体积增大。磁芯体积越大，磁通量越集中，Br越强，互感也越好。因此，随着磁芯参数的增加，互感系数也随之提高。

为了比较上述磁结构的性能，本文计算了各磁结构的效率和磁芯体积，如图5所示。在图5中，磁芯的性能可以用磁芯单位体积的效率η来评价。单位体积η高的发射机具有较低的磁芯体积，但与没有磁芯的发射机相比，它们在η方面的改善不大。相比之下，单位体积η低的发射机比没有磁芯的发射机的η有明显的提高。但由于磁芯体积很大，导致发射机成本高、重量大。因此，不适合选择同时满足单位体积η高和低体积的磁性结构。

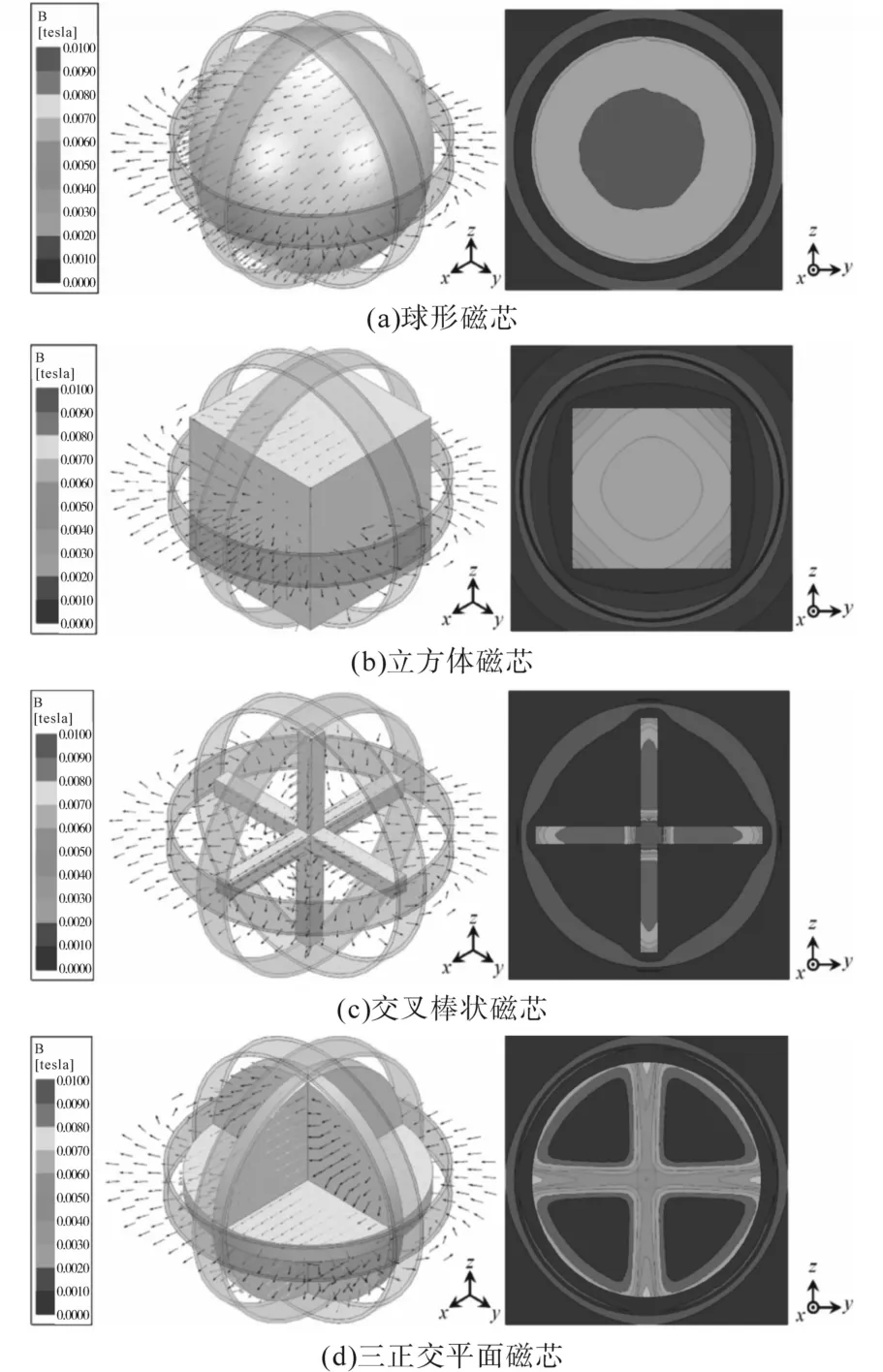
图4 发射器的模拟磁通密度Fig.4 Simulated flux density of emitter

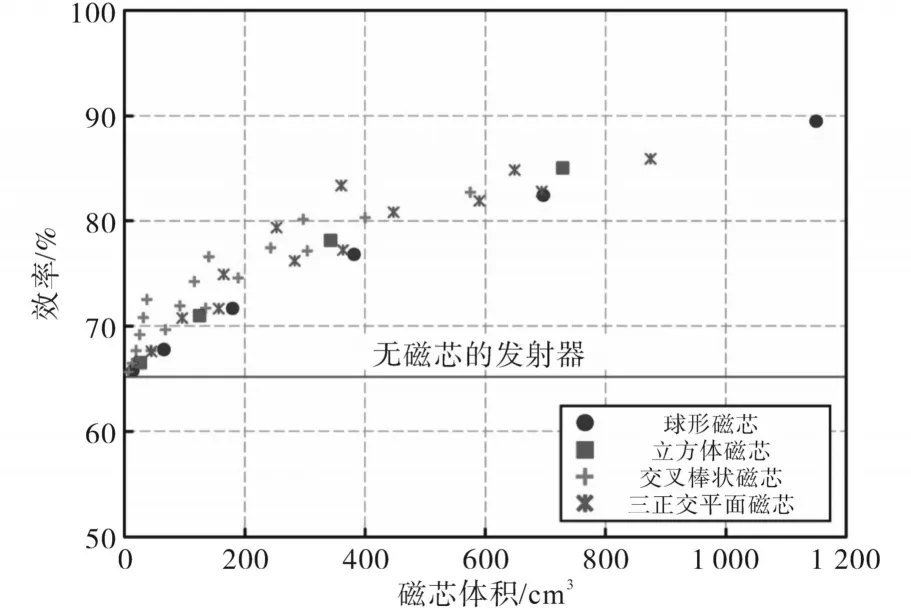
图5 磁芯体积对效率的影响Fig.5 Efficiency versus the volume of the core

2.2 多目标优化设计

多目标优化是指同时优化两个或多个变量的问题[18-19]。本文将其应用于磁结构优化设计时，目标变量为磁芯的效率和体积，设计变量为磁芯参数，约束条件为磁结构不能重叠或穿透发射器。多目标优化是指寻找最优设计变量，使目标变量最小化。因此，为了使目标变量最小，用代替η作为目标变量。由于目标变量的单位和范围不同，采用min-max归一化方法，如下所示：

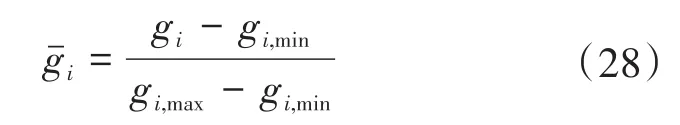
式中：gi为目标变量；gi,max，gi,min是目标变量的最大、最小值；i为gi的归一化目标变量。

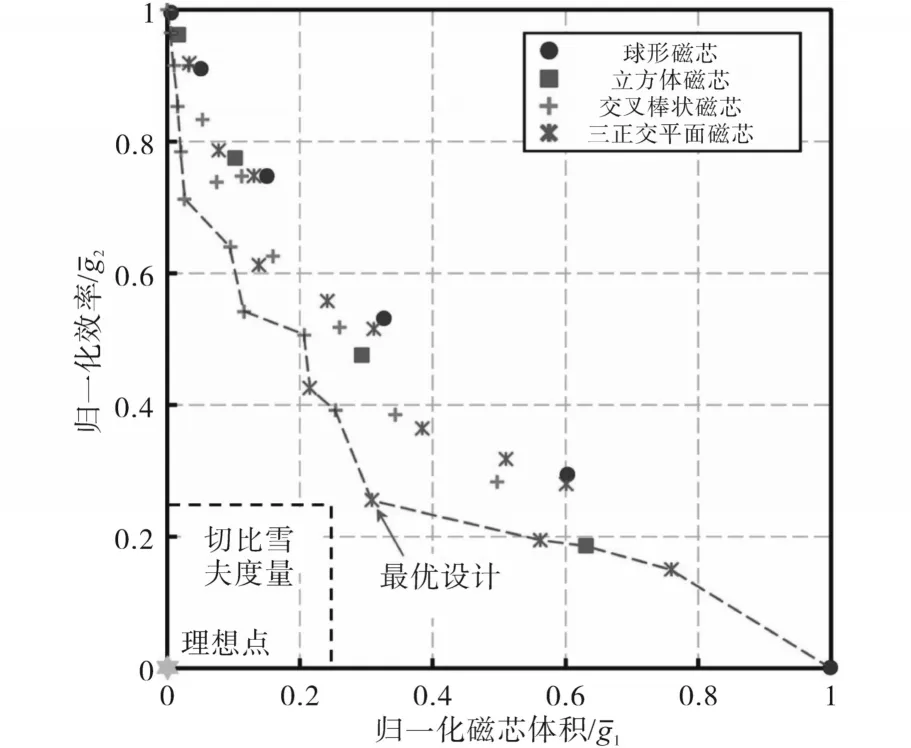
图6 多目标优化结果Fig.6 Results of multi-objective optimization

多目标优化的解不是唯一的，根据目标变量的权重存在各种最优解。这些多目标优化解称为帕累托最优集。选取16个磁结构作为帕累托最优集，如图6所示。

3 实验验证

为了验证所提磁结构的有效性，本文建立了全方位WPT样机，如图7所示。样机的工作原理图见图2，相关参数如下：标准输入电压Vin=50 V，开关频率fs=200 kHz，传统发射器的自感L1=L2=L3=54.7 μH，所提发射器的自感L′1=L′2=L′3=90 μH，接收器的自感L4=54.7μH；传统补偿电容C1=C2=C3=10.8 nF，所提补偿电容C′1=C′2=C′3=7 nF，接收器的补偿电容C4=10.8 nF。

图7 实验结构图Fig.7 Experimental structure diagram

图7中，全桥逆变器采用650 V GaN HEMT，磁芯材质为PM-12，相对磁导率为3 200，最佳磁结构中Dtp=130 mm，Htp=10 mm；发射线圈R=75 mm，N=16。每个发射机电路由全桥逆变器、补偿电容和发射机线圈组成。接收电路由接收线圈组成。其它还有整流器、负载电阻RL等等。接收方是在球坐标系中以P(d,φ,θ)为中心。接收器总是朝向发射机的中心。

图8为在球坐标系下接收器中心为（150 mm，60°，15°）时Il，I2，I3的实验波形。每个发射机线圈电流的参考值由式（5）～式（7）确定，I=4 A。此外，全桥逆变器采用移相控制，以控制发射机线圈电流。

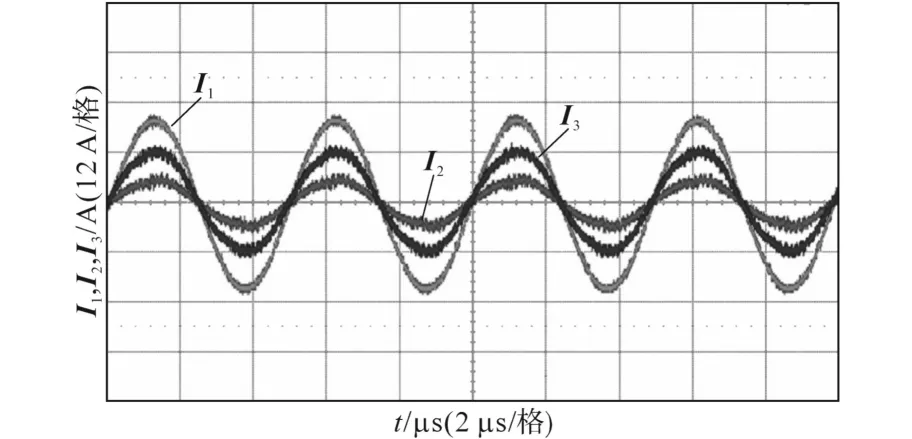
图8 接收器中心位置为φ=60°，θ=15°时I1，I2，I3的实验波形Fig.8 Experimental waveforms of I1，I2，and I3when the receiver is centered at φ=60°and θ=15°

采用如图8所示的电流幅度控制得到以下实验结果。

图9为根据d的效率比较图，在图9中，接收器的中心分别位于（d，0°，0°），（d，45°，45°）和（d，90°，45°），d取值范围为150～220 mm。实线和虚线分别代表实验效率和仿真效率。所设计的系统在所有功率传输距离上，无论接收器位置如何，都比传统系统具有更高的效率。此外，对于所设计的系统，随着d的增加，效率降低的幅度较小。实验结果与仿真结果一致性较好。

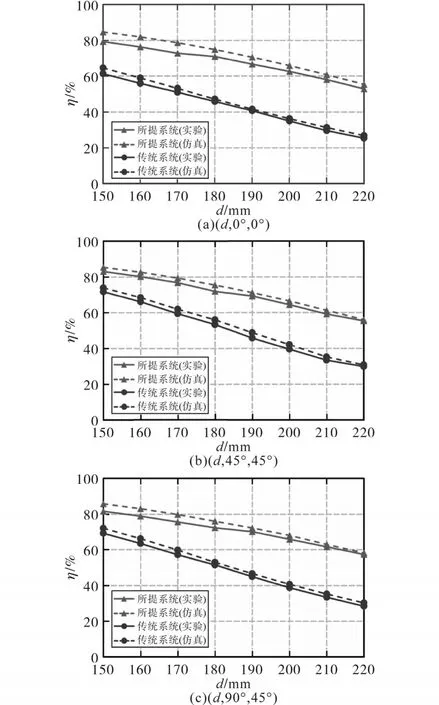
图9 不同接收器的中心位置d下效率的比较图Fig.9 Comparison of efficiencies with respect to d when the receiver is centered at

图10为当接收器以（d，0°，0°）为中心时，KM，Pcore相对于d的变化情况。利用有限元分析软件对KM进行了估算，并计算Pcore。所提系统比传统系统在所有d上具有更高的KM。

图10 接收器中心在（d，0°，0°）时KM，Pcore相对于d 的变化情况Fig.10 KM，Pcorewith respect to d when the receiver is centered at（d，0°，0°）

由图10可知，任意d值下所设计系统的KM值比传统系统都要高得多。这是因为优化的磁结构使得磁通集中，提高了Br值。当d减小时，由于接收器产生的磁通，铁心的磁通密度增大，因此，所设计系统的Pcore增加。然而，Pcore却低至数十MW。忽略式（27）中的Pcore，两个系统中较高的KM都会产生较高的系统效率。图11为与图10相同条件下的计算效率，效率用式（25）计算。

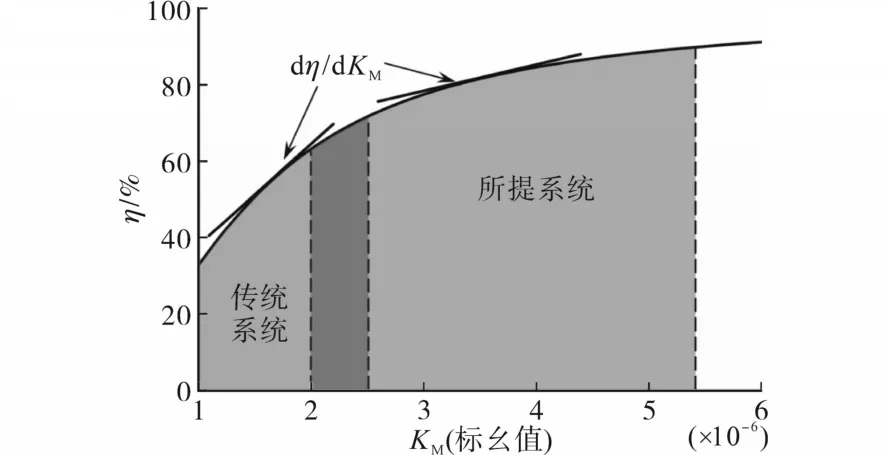
图11 不同KM的系统效率图Fig.11 System efficiency diagram with different KM

图11中，所提系统和传统系统虽然部分区域有重叠，但所提系统的KM一般都高于传统系统。随着KM的增加，效率相对于相互因子KM的变化率降低。因此，虽然随着KM的增加，所提系统的KM比传统系统减少的更多，但所提系统的效率下降的更少。

图12为所提系统与传统系统效率矢量的比较图。

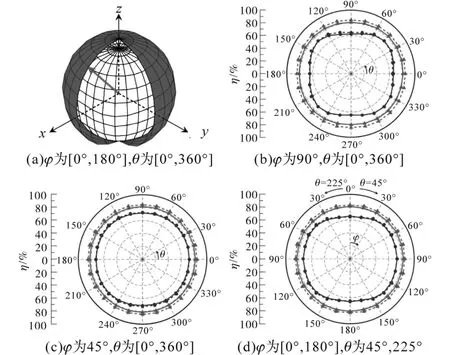
图12 所提系统与传统系统的效率矢量比较图Fig.12 Efficiency vector plot comparison between the designed and conventional systems

图12中，效率用球坐标系中的径向距离表示，d固定为150 mm，发射机最外层到接收器的距离为75 mm。为了进行详细的分析，图12详细描述了效率矢量图的各个横截面，其中，外圈曲线、内圈曲线分别代表所提系统和传统系统；实线和虚线分别代表实验效率和模拟效率。图12b为φ固定在90°，θ从0°变化到360°时的效率，所设计的系统比传统系统具有更高的效率，在所提系统中，在θ=225°时，效率最高为83.0%；在θ=90°时效率提高了18.6%，是三维空间中最大的效率。此外，dη∕dθ的效率相对于θ的变化率较小，因此，效率向量的轨迹非常近似于一个圆，如图12b所示。相比之下，在传统系统中，dη∕dθ较高，因此，效率向量的轨迹就像一个正方形。即与传统系统相比，所设计系统的效率分布相对均匀。图12c为当φ固定在45°和θ从0°到360°变化时的效率，所提系统比传统的系统有更高的效率。在θ=225°时，所提系统的最大效率为82.3%。图12d为φ从 0°到 180°变化时的效率，θ分别为45°和225°，所提系统在所有4个方面都比传统系统有更高的效率，在φ=60°时，所提系统的最大效率为83.0%，所提系统的效率向量轨迹类似于一个圆，传统的效率向量轨迹类似于一个椭圆形。因此，所设计的系统提高了接收器各位置的效率，在三维空间中效率分布均匀。实验结果与仿真结果一致。

图13为所提系统和传统系统在100 W输出功率下的计算损耗。在设计的系统中，Prec是损耗最大的，占总损失的27.7%。PQ,sw和Pc分别占总损失的21.4%和17.5%。设计系统的计算总损耗和测量损耗分别为20.8 W和21.9 W，损失估计误差为5.0%。在传统系统中，PQ,sw为最大的损失组成部分，占总损失的29.7%。Prec和Pc分别占总损失的19.0%和15.7%。根据式（23），Po与KM的平方成正比。传统系统的KM比设计系统低，故要求增加相同的输出功率。因此，PQ,cond，PQ,sw，PDT，PC和Pcoil,cond增大，而传统系统的效率降低。传统系统的计算总损耗和测量损耗分别为32.6 W和35.8 W，损耗估计误差为8.8%。计算结果表明，计算值与实测值吻合较好。造成损耗估计误差的主要原因有：第一，功率损耗模型没有考虑温度。由于功率耗散，功率器件和无源器件的温度升高，改变了寄生参数。第二，由于开关损耗模型假定开关电压和开关电流是线性的，因此没有考虑环流和超调的影响。由于GaN HEMTs的寄生电容很小，寄生电感会导致明显的超调。最后，原型机制造误差也会导致损耗估计误差。磁性结构样机和环形线圈是手工制作的，因此它们的结构与有限元软件模拟的结构并不完全匹配。

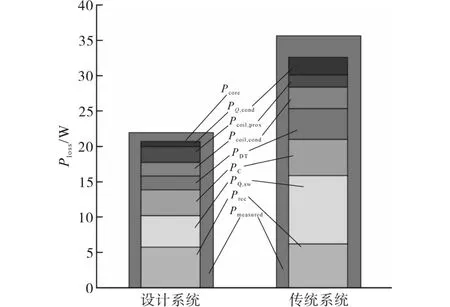
图13 在Po=100 W时，设计系统和常规系统的计算损耗比较Fig.13 Calculated loss comparison of the designed and conventional systems at Po=100 W

4 结论

为了在不增加发射机体积和系统复杂度的情况下提高功率传输效率，本文提出了一种全向WPT系统的最佳电磁结构。首先，详细分析了全向WPT系统的功率损耗，确定了影响系统效率的参数。铁心被插入发射器内部，以避免增加发射机的大小。接着，本文提出了四种磁结构候选方案，并利用有限元分析结果解释了KM改进原理。根据不同的磁芯参数计算了磁芯的效率和磁芯体积，并通过多目标优化设计选择了最优磁芯结构，实现了磁芯体积和效率的均衡。根据所设计的参数制备了最优磁结构，建立了全方位WPT样机。最后，通过仿真和实验，结果证明所提方法的有效性和优越性。