计及短路直流分量的支路断路器开断能力校核
曹炜,桂世成,黄阮明,何必伦,钦焕乘
(1.上海电力大学电气工程学院,上海 200090;2.国网上海市电力公司经济技术研究院,上海 200233)
随着我国负荷需求不断增加,电网的规模与容量不断扩大,短路电流的超标问题也越来越严重。部分电网中出现了断路器短路电流遮断容量不足的问题[1-2],因此需要更准确地校核断路器的遮断容量。传统校核断路器遮断容量能否满足要求的方法是将故障点短路总电流周期分量计算值与断路器的额定开断电流进行比较,从而判断短路电流是否越限。但在实际发生短路时,流经断路器的短路电流与网络接线方式、断路器动作顺序有关,并不一定与故障点的短路电流相同。因此,传统的断路器遮断容量校核方法并不完全准确,会使针对该断路器的短路电流限制措施有所不同。过于乐观的校核结果可能会导致短路故障无法快速切除,造成系统稳定性下降。反之,过于保守的校核结果会增加多余的限制短路电流的设备,造成投资浪费。因此,计算流经断路器设备的最大短路电流而非故障点总的短路电流十分重要。此外,断路器安装地点的温度、海拔高度以及电磁干扰等环境因素都或多或少会影响断路器的开断能力[3]。
由于节能降耗的要求,随着电力设备的X∕R比值的增大,短路电流直流分量衰减速度也越来越慢,对断路器实际开断能力的影响也越来越明显[4-5]。因此,在断路器的遮断容量校核中考虑直流分量对断路器开断能力的影响也是必要的。而传统的短路电流直流分量计算方法有国标GB∕T15544.1—2013《三相交流系统短路电流计算》建议采用的等效频率法[6]、行业标准NB∕T35043—2014《水电工程三相交流系统短路电流计算》建议采用的极限频率法[7]。上述方法仅限于计算短路点总的直流分量,无法计算流经断路器的直流分量衰减时间常数。
此外,高压交流断路器标准[8]中明确规定了断路器开断成功应该满足的条件,但在实际电网中存在的直流分量衰减时间常数超标问题标准中并未给出解决方法。IEEE C37.010标准[9]中采用E∕X法考虑短路电流交流分量和直流分量的衰减,如果故障时的E∕X超过断路器最大对称开断能力的80%应该多乘一个折减系数。文献[10]中介绍了三种考虑直流分量超标的等效折减方法,其中矩形累计电荷等效法最为保守。
本文在以上工作的基础上应用阻抗修正的支路短路电流直流分量计算方法,并根据断路器的动作顺序分析流过断路器的短路电流的差异,从而确定流过断路器的最大短路电流。基于华东某实际电网算例采用折减系数法校核比较了断路器分支中的最大可能短路电流和短路位置处的短路电流周期分量,以表明所提出的方法与传统方法之间的差异。
1 断路器校核中折减方法对比
1.1 标准中对断路器开断的要求
额定短路开断电流在国标《GB1984—2014—交流高压断路器》[8]中给出的定义为在国标规定的使用和性能条件下,断路器所能开断的最大短路电流。在标准中,表征额定短路开断电流特征的主要为:交流分量有效值及断路器动作瞬间的额定短路开断电流的直流时间常数。值得注意的是:
1)断路器动作时的直流分量百分数不超过20%,额定短路开断电流仅需由交流分量的有效值表征;
2)直流分量百分数是额定短路开断电流的直流时间常数和短路电流起始时刻的函数。
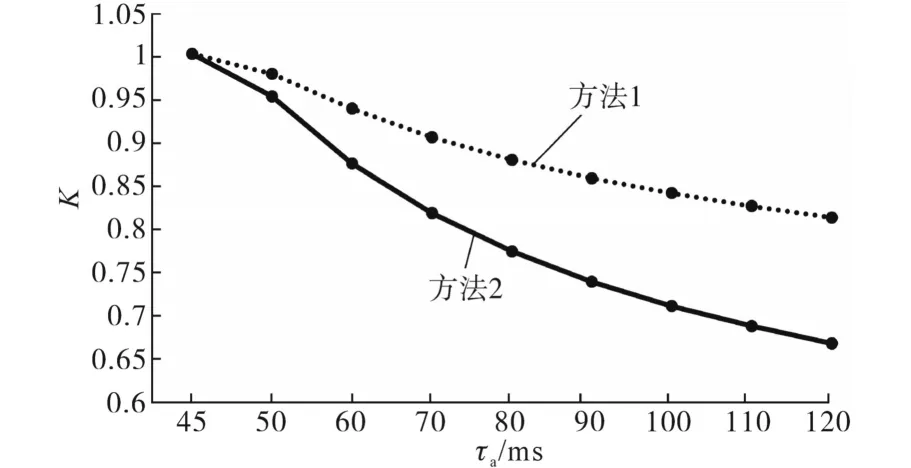
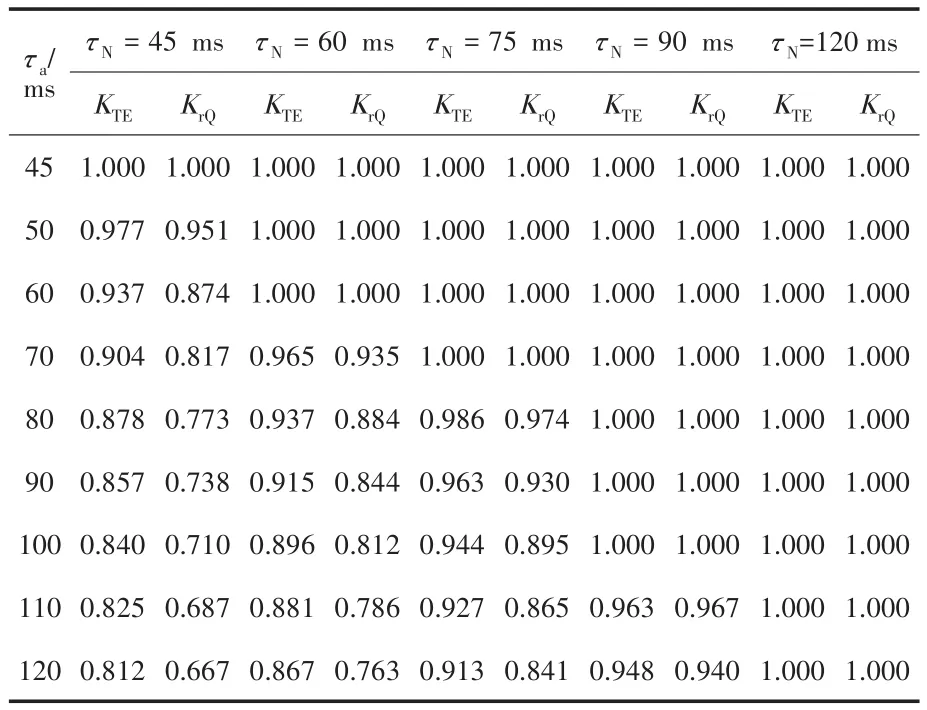
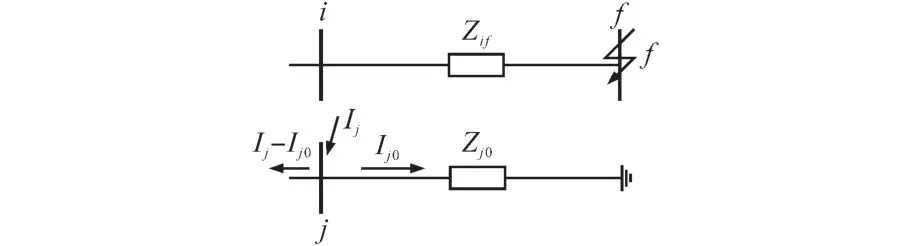
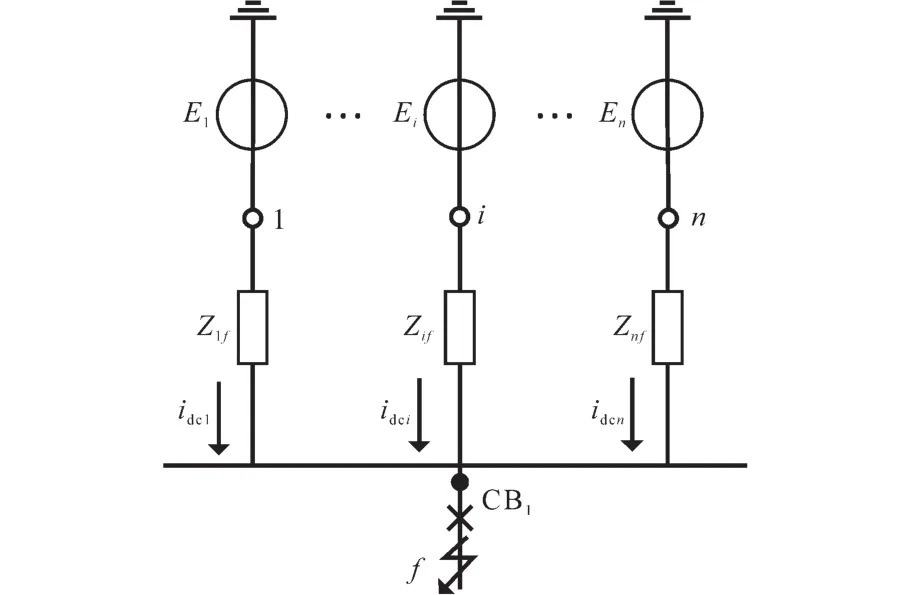
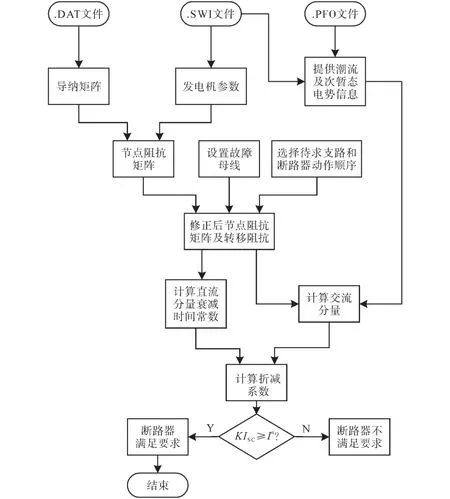
在上述条件中,断路器应能开断直到额定短路开断电流的任一短路电流,该电流包含直到额定值的任一交流分量及与其相关规定的直流时间常数对应的任一直流分量。《GB1984—2014—交流高压断路器》中明确规定了选择断路器时对开断电流的要求,同时开断电流中包含了对直流分量的要求。从短路电流工程计算角度出发,并不追求完整的瞬时电流曲线,而是需要计算出具有意义的特征量:断路器开断电流交流分量Ib、断路器开断电流直流分量衰减时间常数τdc(idc),断路器成功开断时短路电流需要同时满足以下条件:①I″ 在实际情况中普遍存在满足条件①,但不满足条件②的情况。假设断路器额定开断时间常数为τN=45 ms,电网中实际短路电流直流分量时间常数为τa=60 ms。由图1可知,大半波的持续时间会增加、峰值增大。 图1 不同直流时间常数下的短路电流波形Fig.1 The waveforms of short-circiut current with different DC time constant 由1.1节图1中的波形,根据《IEEE Std C37.010》[9]和《GB 1984—2014高压交流断路器》[8]两个标准分别推演出全电流等效法和矩形累计等效电荷法。 1.2.1 全电流等效法 全电流等效法基于IEEE C37.010标准中的介绍进行推导,利用全电流有效值在一个周期内进行等效折减,用全电流等效折减系数KTE以表征断路器开断能力的下降: 式中:τN为断路器额定直流分量时间常数;τa为实际电网中的直流时间常数;t为断路器开断时间。 1.2.2 矩形累计等效电荷法 矩形累计等效电荷法考虑最后大半波的峰值电流和持续时间围成的矩形,在τN>τa时,利用最后半波矩形累积电荷相等的原则,得出用矩形累计等效折减系数KrQ表征断路器开断能力的下降: 式中:t1,分别为断路器和实际电网开断于大半波时的起始时间;t2,分别为断路器和实际电网开断于大半波时的结束时间。 实际上,全电流等效法和矩形累计等效电荷法都是等效能量法的不同形式,其中全电流等效法利用电流有效值在一个周期内进行等效折减,而矩形累计等效电荷法利用的是最后大半波的实际波形和峰值电流围成的矩形波形进行电荷等效折减。 在实际工程中,断路器多在短路后第三个周波的大半波中,假设断路器开断时间t=40 ms,将两种方法的折减系数在不同的额定时间常数和电网实际时间常数中进行比较,如图2和表1所示。如图2所示,表示断路器额定开断时间常数为45 ms时,不同电网实际直流分量时间常数下断路器开断电流能力的折减系数K下降趋势图,其中,方法1表示全电流等效法,方法2表示矩形累计等效电荷法。如表1所示当τa≤τN时,断路器开断能力没有下降,折减系数为1;当τa>τN时,相同情况下KTE>KrQ。因此采用全电流等效法校验断路器的结果最为乐观,采用矩形累计等效电荷法的结果最为保守。而目前全电流等效法采纳的范围最为广泛,不论是《IEEE Std C37.010》标准[9]还是教科书《发电厂电气部分》[3]中均使用的是该方法。 图2 τN=45ms时的折减系数下降趋势Fig.2 Downward trend of reduction factor whenτN=45ms 表1 不同时间常数下2种方法折减系数Tab.1 Reduction factor of two methods under different time constants 目前国内常用的机电暂态仿真软件均无法计算分支中短路电流直流分量。电磁暂态仿真软件虽能准确得到故障时支路中短路电流波形,从而分离出直流分量及衰减时间常数,但电磁暂态仿真工作量大,不适合应用于实际大规模电网中。 图3为电力系统网络发生故障后的局部结构图。母线i,j,f均为系统中的节点,当母线f发生故障时,目前的方法仅能计算母线f处总的短路电流(即iif+ijf)的直流分量衰减时间常数。而分别计算支路中iif和ijf的短路电流直流分量衰减时间常数则需要进行网络变换。接下来将介绍网络变换的网络模型。 图3 电力系统故障局部示意图Fig.3 Partial schematic diagram of power system failure 在进行网络变换前需要求取节点阻抗矩阵。使用支路追加法建立节点阻抗矩阵的优点在于,修改与部分网络耦合的树枝支路时不必生成整个阻抗矩阵,减少了工程中的计算量。因此本文采用支路追加法对需要变换的支路进行修改,获得网络变换后的节点阻抗矩阵。 假设计算图3中支路(i,f)的直流分量时间常数,首先需要在支路(j,f)支路上追加阻抗值为-Zjf的支路,如图4所示。 图4 追加支路示意图Fig4 Schematic of additional branch 追加-Zjf的支路后会引起网络中各个节点的电压变化,为了保持原有各个节点的注入电流不变需要对节点阻抗矩阵中元素进行修改。设原网络中注入母线f和母线j的短路电流分别为If和Ij。当母线f和母线j之间追加-Zjf后,母线f的注入电流变为If-Ifj,母线j的注入电流变为Ij+Ifj。此时可以计算出系统网络中任意节点母线i的电压为 式中:Vi为母线i的电压值;Zim,Zif,Zij分别为母线i与母线m、母线f、母线j之间的互阻抗;Im为注入母线m的电流;Ifj为追加-Zfj连支上的电流;n为网络节点数。 式(5)中i=j和i=f时得到如下等式: 式中:Zjj,Zff分别为母线j、母线f的自阻抗。 由式(5)~式(7)可求得如下关系式: 由式(8)可知,网络中母线i与母线m之间修正的互阻抗Z′im为 此时,系统网络已完成待求支路的拆分,还需要在母线j处需要追加阻抗值为Zjf的接地连支Zj0。如5图所示,当追加接地连支Zj0后,原网络中母线j注入电流由Ij改变为Ij-Ij0。 图5 网络中追加接地连支Fig.5 Add ground connection to the network 此时系统网络中任意节点i的电压为 式中:Vi为母线i的电压值;Zim,Zij分别为母线i与母线m、母线j之间的互阻抗;Im为注入母线m的电流;Ij0为追加接地连支Zj0上流过的电流。 接地连支Zj0上的电压方程为 由式(10)~式(11)得: 将式(12)代入式(10)中得: 由式(12)可知,网络中节点i与节点m之间修正的互阻抗为 在计算待求支路上短路电流直流分量时,只需通过式(9)和式(14)修正原网络阻抗矩阵中的元素,在母线f处设置故障,计算所得短路电流即为待求支路上的短路电流。 文献[11]考虑了不同的动作顺序,计算流过断路器所在支路上的最大短路电流。图6为所校验的本侧断路器首先开断时短路电流示意图,断路器CB1和CB2安装在支路(i,j)上。 图6 CB1首开流过的短路电流i1,i2Fig.6 The short circuit current i1,i2that CB1first flows through 在图6中,i1为在k1发生短路时流过CB1的短路电流,i2为在k2发生短路是流过CB1的短路电流。 图7为对侧断路器CB2先于本侧断路器CB1开断时的情况,此时流过断路器的短路电流为i3。 图7 CB1次开流过的短路电流i3Fig.7 The short circuit current i3that CB1second flows through 传统校验断路器开断能力采用故障点短路总电流周期分量,即短路点k1和k2处的短路电流为i1和i2之和(图6中称为i4)。而校验断路器CB1开断能力应该是流过CB1的最大可能电流,即考虑了直流分量影响后i1,i2和i3中最大的电流,而不是i4的周期性分量电流。 利用转移阻抗原理,可将多电源复杂网络化简为如图8所示的多电源线性网络。 图8 多电源简化示意图Fig.8 Simplified schematic of multiple power supplies 由图8所示节点f的直流分量衰减时间常数是由化简后各条支路提供的直流分量之和,而各条支路的直流分量衰减时间常数Tif由支路参数决定,支路i的衰减时间常数Tif计算公式为 其中 式中:Zif为转移阻抗;Rif为转移电阻;Xif为转移电抗;ω为角速度。 转移阻抗计算公式为 式中:zi为电源Ei的内阻抗;Z′ff为网络变换后短路点f的自阻抗;Z′if为网络变换后电源点i与短路点f之间的互阻抗。 在国标《GB∕T 15544.1—2013》中有明确规定,可以直接根据次暂态初始电流I″k计算短路电流的最大直流分量idc: 式中:I″k为次暂态短路电流初始值;t为短路故障开始后的时间;T为短路电流直流分量衰减时间常数。 根据叠加原理,计算故障点总的直流分量idc∑的表达式为 式中:idci为第i条支路中的短路电流直流分量;I″ki为第i条支路次暂态短流电流初始值;Tif为第i支路中的直流分量衰减时间常数。 复杂系统中,短路点总的直流分量衰减时间常数表达式为 式中:idc0i为第i条支路中短路电流直流分量初值;idc0∑为短路点总的直流分量初值。 图9为断路器开断能力校验计算流程图。 图9 计算流程图Fig.9 Calculation flow chart 本文基于BPA数据平台,根据图9所示流程,实现数据读取计算支路短路电流直流分量衰减时间常数,并判断该支路上的断路器是否符合要求。具体步骤如下: 1)分别读取.DAT文件、.SWI文件和.PFO文件中的网络参数,形成节点阻抗矩阵; 2)设置故障母线,选择待求支路及断路器动作顺序,进行网络变换,修正节点阻抗矩阵,计算转移阻抗; 3)计算短路电流交流分量和直流分量衰减时间常数;计算折减系数,判断断路器是否满足开断要求。 本文首先以IEEE39系统作为算例,如图10所示。在PSCAD电磁暂态软件中建立IEEE39节点电力系统仿真模型,并在BUS15和BUS18两个母线处设置三相短路故障,通过仿真得到故障点所连相关支路上的短路全电流波形,并从波形中分离出各支路的短路电流直流分量波形从而得到直流分量衰减时间常数。表2为本文方法计算结果与PSCAD仿真结果的比较。由表2可知,本文应用的方法与电磁暂态仿真结果值相对误差不超过2.99%,可以说明本文方法具有较高的准确性。 图10 IEEE39标准算例示意图Fig.10 Schematic of the IEEE39 Examples 表2 短路各支路中直流分量衰减时间常数Tab.2 The decay time constant of the DC component in each branch of the short circuit 本文以华东某实际电网数据作为依据,对电网中部分500 kV电压等级的厂站分别计算出线支路及母线上短路电流的周期分量和直流分量衰减时间常数如表3、表4所示。设断路器的额定开断电流为63 kA,断路器在发生故障后时触头刚分,550 kV电压等级的断路器标准直流分量时间常数为45 ms。表3中支路的次暂态取值为2.3节中考虑开断顺序后流过断路器的可能最大短路电流周期分量。 表3 某电网厂站出线支路短路电流计算结果Tab.3 The calculation result of short-circuit current of branch in some power grid 表4 某电网厂站母线短路电流计算结果Tab.4 The calculation result of the total short-circuit current of bus in some power grid 由表3、表4结果可知,如XH,TW等厂站,虽然采用母线上短路电流总的次暂态电流和直流分量衰减时间常数校验断路器开断能力不满足要求,但采用断路器所在支路上的短路电流总的次暂态电流和直流分量衰减时间常数校验断路器开断能力仍满足要求。此外,也有部分厂站存在采用全电流等效法校验满足要求,但采用矩形累计等效电荷法校验不满足要求的情况。 1)在实际电网中,直流分量衰减时间常数可能达到90~120 ms,因此在检验断路器开断能力时应考虑直流分量的影响。本文涉及全电流等效法和矩形累计等效电荷法,其中矩形累计等效电荷法的折减系数普遍小于全电流等效法的折减系数。在断路器选型和规划运行时建议采用矩形累计等效电荷法。 2)本文结合基于追加支路的转移阻抗方法计算与故障节点相连支路上的短路电流直流分量衰减时间常数,并与PSCAD电磁暂态仿真结果比较,本文涉及方法具有较高的准确性。 3)由计算结果可知,母线上总的短路电流周期分量和直流分量会大于支路上的周期分量和直流分量,因此校验断路器开断能力应采用流过断路器所在支路的短路电流,以避免低估断路器的开断能力。
1.2 考虑直流分量的断路器校核折减方法
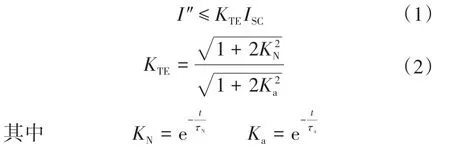
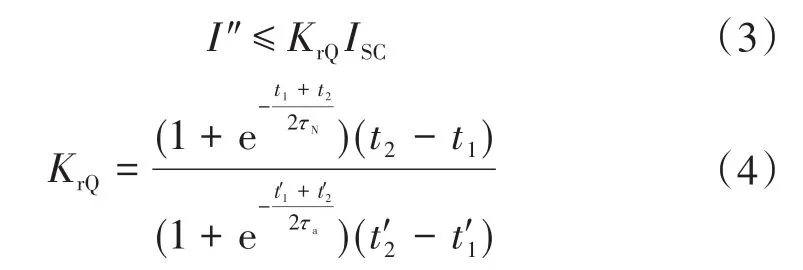
1.3 折减系数对比
2 分支短路电流直流分量计算方法
2.1 分支直流分量时间常数计算

2.2 网络变换

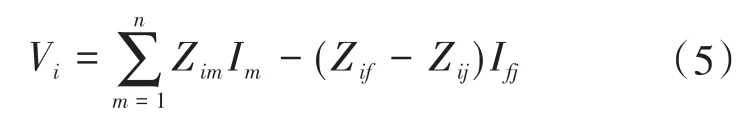
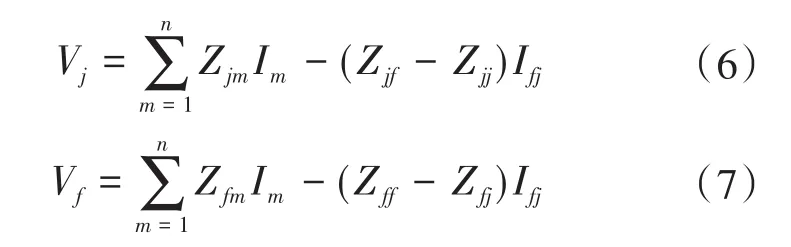
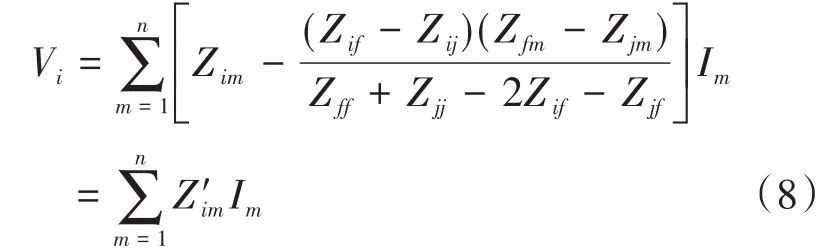
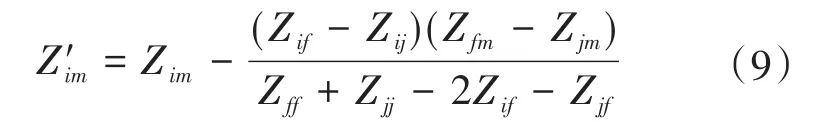
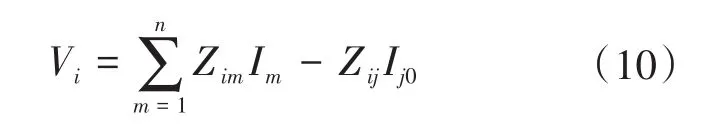

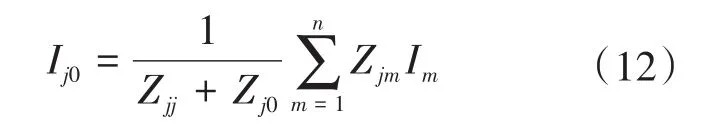
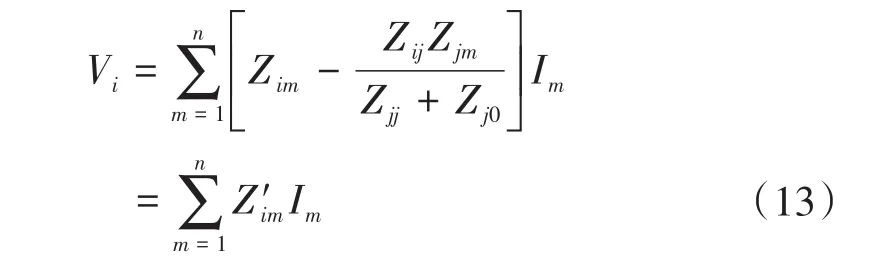
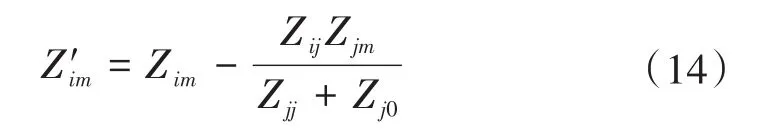
2.3 考虑断路器动作顺序


2.4 衰减时间常数计算方法
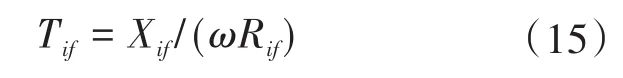
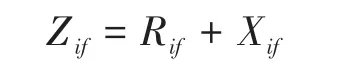

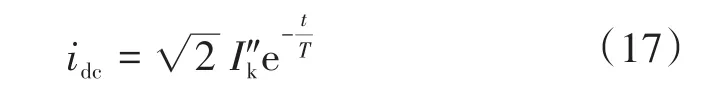
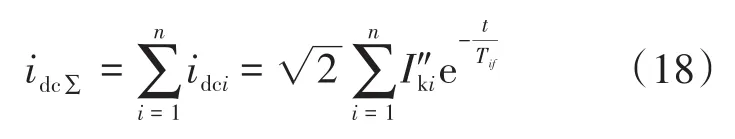
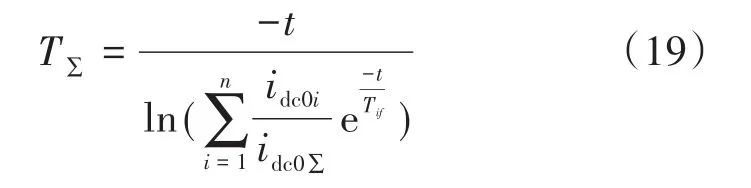
3 断路器开断能力校验计算流程
4 算例分析
4.1 直流计算方法检验
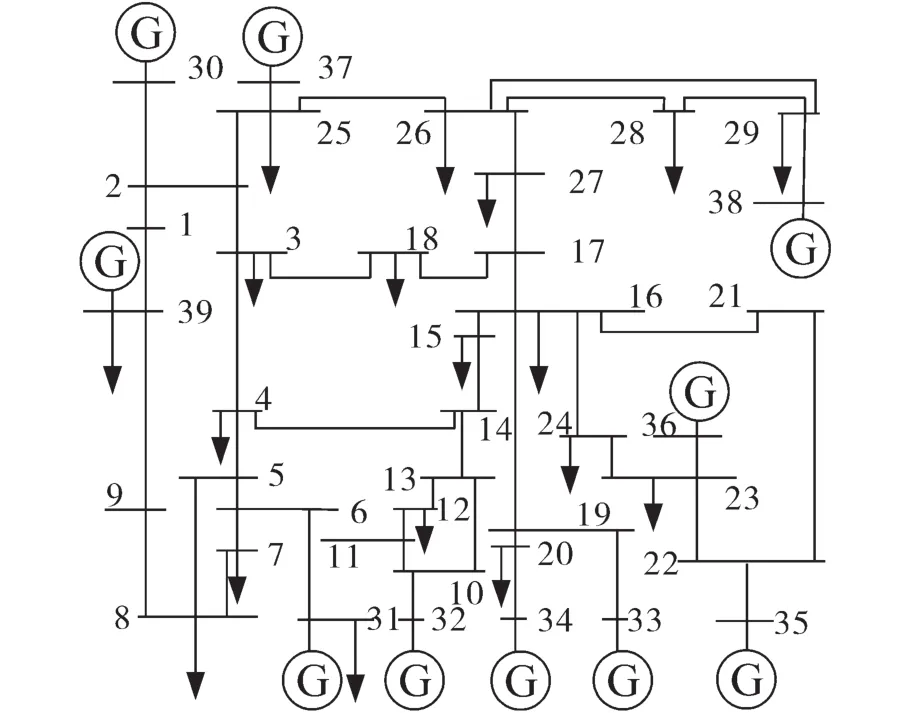

4.2 与传统方法比较
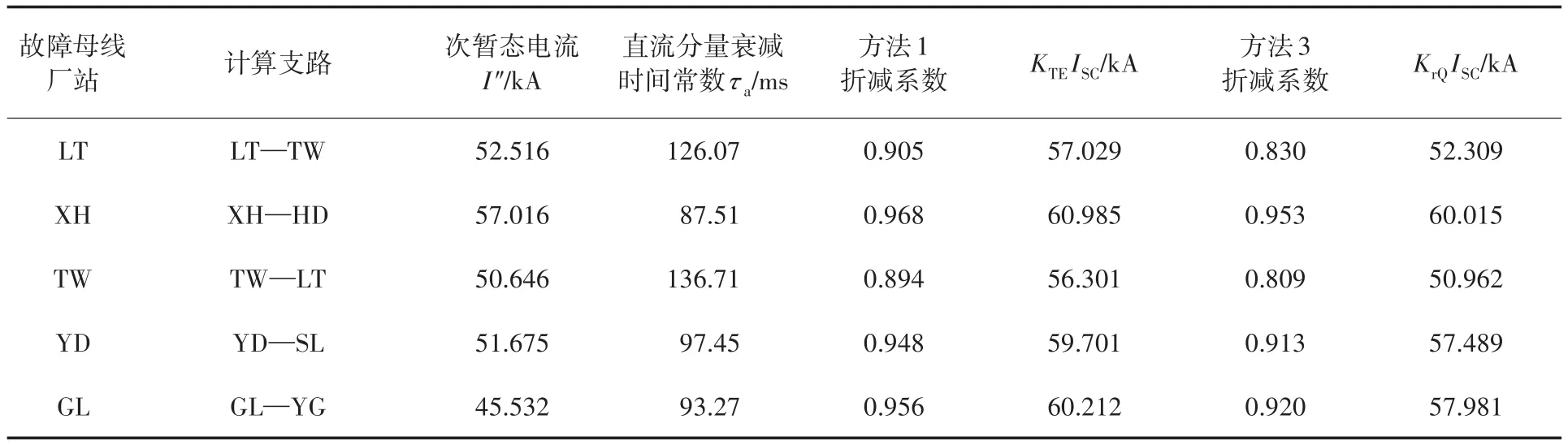
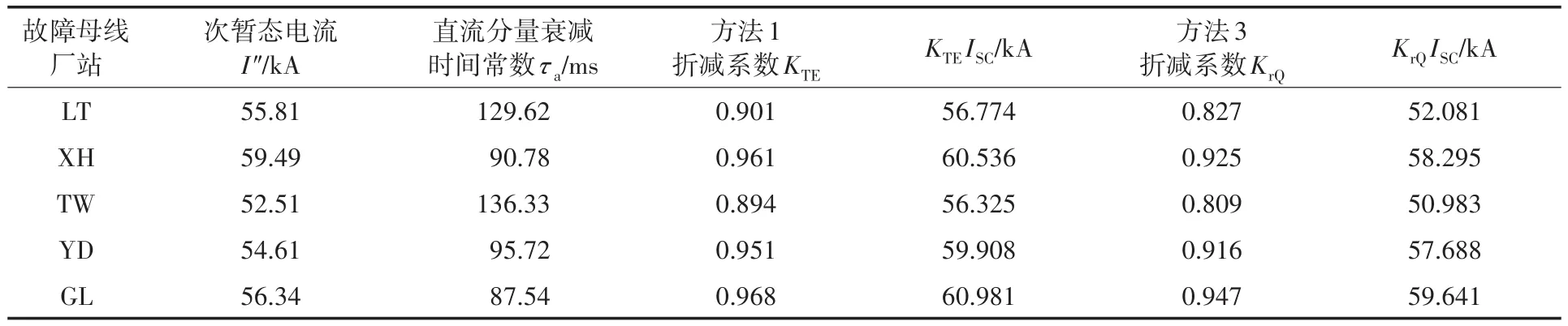
5 结论

