改进一阶LADRC的微网逆变器零序环流抑制

周雪松，郭凯瑞，马幼捷，钟伟宝

（1.天津理工大学天津市复杂控制理论重点实验室，天津 300384；2.天津理工大学电气电子工程学院，天津 300384）

随着世界能源的短缺，微电网因优化了分布式能源的终端效率成了当前关注的热点[1-2]。微电网通常采用电力电子变换器作为微源电能变换的接口。随着系统所需容量增大，传统的单台逆变器易受到开关频率等限制达不到满意的输出功率。因此，在高功率应用中采用模块化并联拓扑结构成为一个理想趋势[3]。将电压源进行模块化并联后，增加了系统容量，但两逆变器间形成了零序环流（zero-sequence circulating current，ZSCC）的路径。当系统线路参数不相等、开关动作不一致时，形成的零序电压作用于逆变器之间的等效电阻便会产生零序环流[4-6]。零序环流严重影响系统输出的电流质量，因此抑制零序环流是一项重要的工作。

近年来，国内外学者对零序环流抑制方法的研究主要有两方面：一方面是硬件上通过交流侧放置隔离变压器抑制形成环流通路[7]，然而隔离变压器体积大、成本高，不具有实用性。另一方面从控制的角度考虑。文献[8]针对零序环流形成机理的分析，采用了比例积分（proportional-in⁃tegral，PI）控制的方法来抑制零序环流。PI控制器的适用范围大，但会受到带宽限制达不到最佳性能。文献[9]中将PI控制与前馈控制相结合对零序电流环的带宽进行了扩展，提高了环流控制效果。文献[10]设计了零序环流自抗扰控制器，将变零矢量策略与线性自抗扰控制（linear active disturbance rejection control，LADRC）结合，引入线性扩张状态观测器（linear expansion state observer，LESO）对系统的总扰动进行观测补偿，有效抑制环流。

本文搭建了两台微网逆变器并联结构模型，分析了零序环流产生的机理。提出了一种基于观测误差补偿总扰动的改进型线性自抗扰控制策略，在线性扩张状态观测器（LESO）估计总扰动后，采用误差补偿的思想，通过改进控制律来减小观测器的误差，准确地补偿外部扰动，以提高控制器的性能，更好地抑制零序环流。

1 并联三相逆变器系统建模厔变零矢量调制厅理

1.1 并联三相逆变器系统建模

搭建了如图1所示的两台共直流母线的微网逆变器并联结构图。

图1 微网逆变器并联结构图Fig.1 Parallel structure diagram of microgrid inverter

图1中，idc为直流侧电容器的电流；udc为直流侧母线电压；C为总线滤波电容器；Llj（l=1，2，3，4，5，6；j=1，2）分别为开关管；Lj，Rj分别为第j台逆变器的等效滤波电感及电阻器；uaj，ubj，ucj和iaj，ibj，icj为第j台逆变器的输出电压和输出电流；ea，eb，ec为交流侧三相电压。

系统中零序环流为

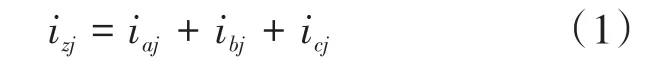
式中：izj为第（jj=1，2）台逆变器的零序环流。

相应的可将零序占空比定义为dzj=daj+dbj+dcj，零序电网电压定义为ez=ea+eb+ec。

根据图1所示结构，结合基尔霍夫定律可以得到如下状态方程：

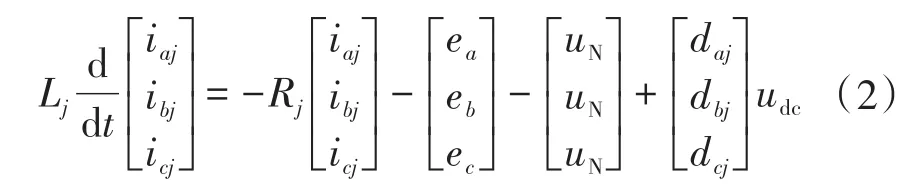
式中：uN为每相桥臂的中性点电压；daj，dbj，dcj为逆变器j的每相桥臂的占空比。

为获取零序分量，从abc坐标系转到dqz坐标系的状态空间方程为

式中：ω为电网侧的基波角频率。

两台逆变器零序电流大小相等方向相反，因此可得iz=iz1=-iz2，结合式（3）得到零序环流的状态空间方程为

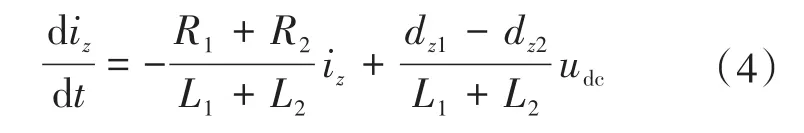
根据式（4）可知，零序环流的存在与零序占空比、系统的硬件参数和直流侧电容电压有着对应关系。

1.2 零序环流变零矢量调制

空间矢量脉宽调制（space vector pulse width modulation，SVPWM）策略中的空间状态矢量由六个非零矢量和两个零矢量组成。设一个开关周期内d2，d3分别为非零矢量U2，U3的占空比，d0为零矢量U0与U7总的占空比，则1=d0+d2+d3。不同的控制方法下，U0与U7分别对应的占空比不同，但d0不变。系统输出不会因零矢量作用时间的变化而改变，因此可调节U0和U7分别对应的占空比来改变零序占空比，从而减小零序环流。

PWM逆变器零序占空比为[11]

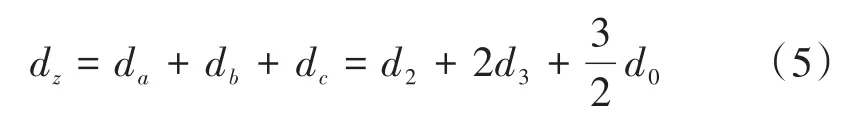
使用零矢量分配因子k后重新调整其作用时间，使两台逆变器零序占空比差值为零，开关管动作一致从而抑制零序通道的形成。变零矢量调节后的三相占空比分配如图2所示，其中Sj（j=a，b，c）为开关函数，T为开关周期。调节后的零序占空比为

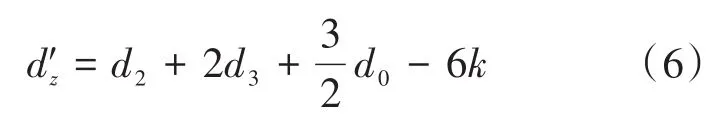
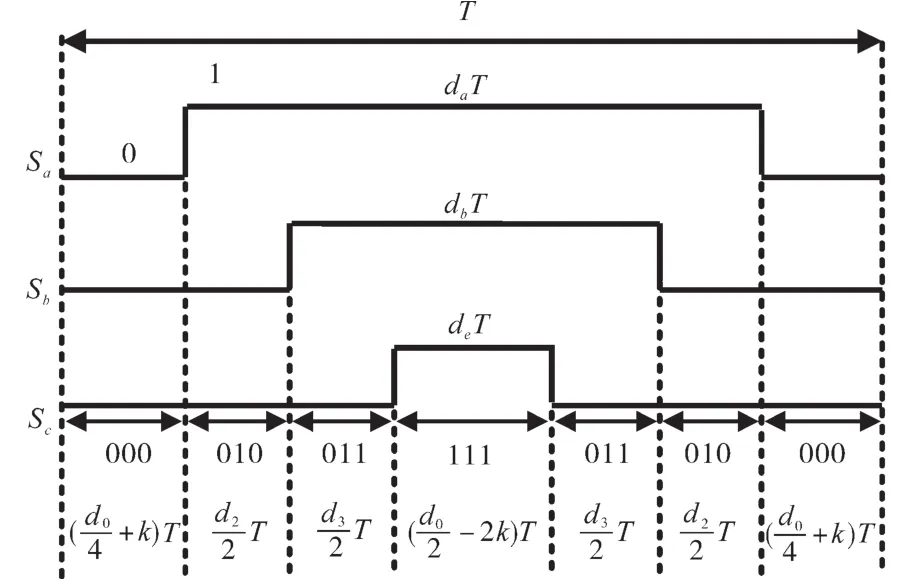
图2 变零矢量SVPWM的三相占空比Fig.2 Three-phase duty cycle of variable zero vector SVPWM

本文将抑制逆变器1的环流，令k1，k2分别为第一、二台逆变器的零矢量分配因子，k2=0。理想条件下可得到零序环流的数学模型如下所示：

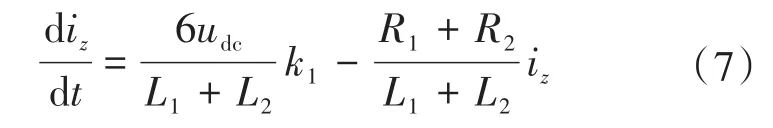
选用合适的控制器后便可得到k1。

2 零序电流环改进型LADRC控制器的设计

传统LADRC主要由线性跟踪微分器（linear tracking differentiator，LTD）、线性扩张状态观测器（LESO）以及线性状态误差反馈控制律（linear state error feedback，LSEF）组成。其中LTD主要用于安排过渡过程，系统产生的零序环流需要快速跟踪给定电流，因此不使用LTD。LSEF综合干扰估计补偿并产生控制信号。LADRC控制器将系统的未知扰动、参数不确定性和耦合都归算于总扰动，通过LESO对其观测来估计补偿总扰动，然后利用LSEF将积分串联型系统转化为期望的闭环系统，由此可以得到期望的闭环动态特性，并且不受限于被控对象的具体数学模型。

文中选用改进型LADRC控制器来获取k1。下面对改进型LADRC控制器进行设计。

2.1 LADRC控制器的结构设计

假设udc恒定，式（7）可以看做是一阶系统，被控对象的状态方程可写为

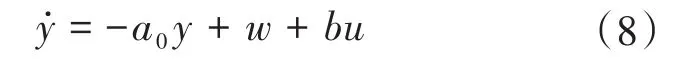
式中：a0为该系统的参数；w视为未知扰动；b为系统输入的控制器增益，可将b0作为它的已知部分；u为控制器的输出；y为被控对象的输出。

令x1=y而（fy，w）=-a0y+w+（b-b0）u为系统的总扰动，h为总扰动的微分。系统的状态方程可列为

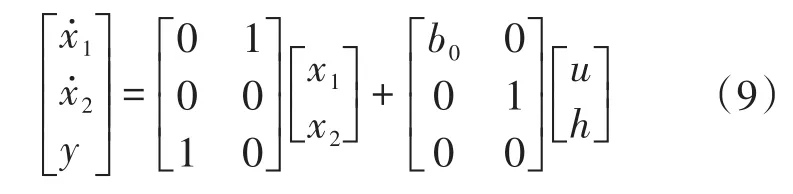
建立二阶LESO的状态方程：

式中：z1为y的跟踪值；z2为总扰动f的跟踪值；β1，β2为LESO的增益系数，选取合适的β1，β2使LESO能够实时跟踪系统中的各个变量。

状态观测器对应的特征方程为

设LESO的带宽为ω0，为了便于控制器的设计，将极点配置在观测器的带宽处可得：

该系统设计的是一阶LADRC，不存在对状态变量微分的观察，线性状态误差反馈算法为

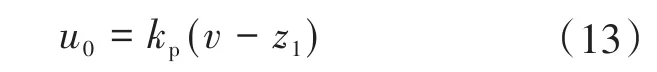
式中：kp为比例控制系数；v为零序环流的给定值。

传统LSEF的设计为

假设z2能够很好地跟踪上总扰动（fy，w），则系统可以补偿为一个串联积分的形式：

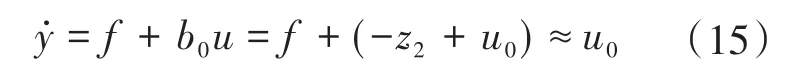
由式（13）～式（15）可得系统的闭环传递函数：

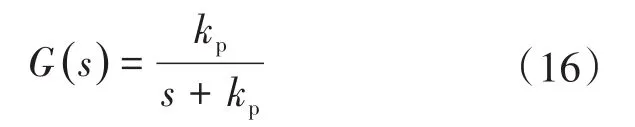
令ωc为比例控制器的带宽，根据极点配置同样可以得到kp=ωc。

2.2 线性状态误差反馈控制律的改进设计

根据式（15）可知，LADRC通过LESO对总扰动的实时估计来进行扰动补偿，所以总扰动的不确定性对LESO有着关键的影响。因此，研究LADRC控制器的结构优化，使其能够减小观测误差，准确补偿外扰，具有重要现实意义。

2.2.1 总扰动对LESO影响的分析

定义二阶LESO的估计误差为

由式（9）、式（10）可得估计误差的状态空间方程为

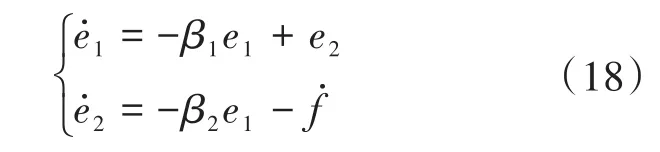
经过拉普拉斯变换后可得总扰动与估计误差之间的传递函数为

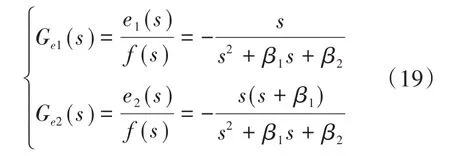
由式（19）可得，总扰动的不确定性与LESO的估计误差产生有着唯一联系。本文将采用改进LSEF来补偿扰动项，减小扰动信号对闭环系统的影响。

2.2.2 LSEF的改进

考虑LESO的估计误差后实际所对应的系统为

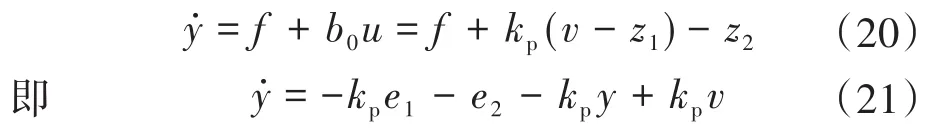
将理想闭环外的误差项定义为

将其误差项抵消后，理想闭环系统为

带有LESO估计误差补偿的LSEF控制器的输出为

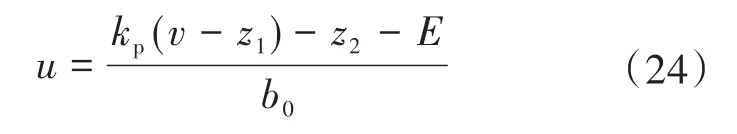
E为一个理想误差，无法直接获取到，可将E转换为已知变量的函数，根据式（17）、式（18）可得：

式（25）经过拉普拉斯反变换并带入式（22）可得：

误差e1可直接获取，进行不完全误差补偿，忽略无法直接得到的微分项，则

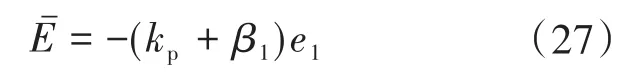
式中：为忽略微分项的误差，即不完全误差。改进后的LSEF控制器的输出为

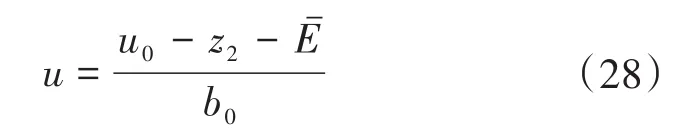
改进后的一阶LADRC结构图如图3所示。

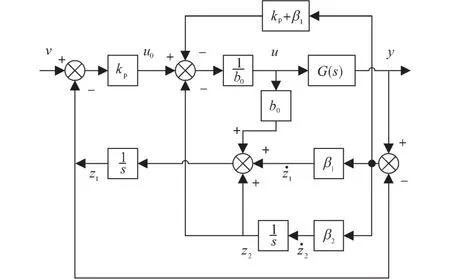
图3 改进型一阶LADRC结构图Fig.3 Improved first-order LADRC structure diagram

3 改进型一阶LADRC控制器的性能分析

3.1 抗扰性分析

LADRC的设计主要是参数ω0和ωc的设计，下面分析两个参数对控制系统性能的影响[12]。

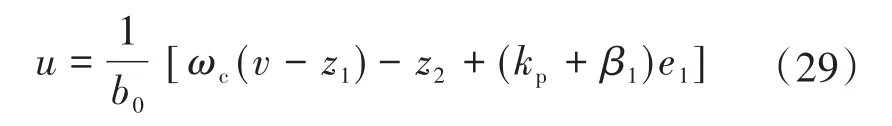
在频域中控制器的输出可表示为

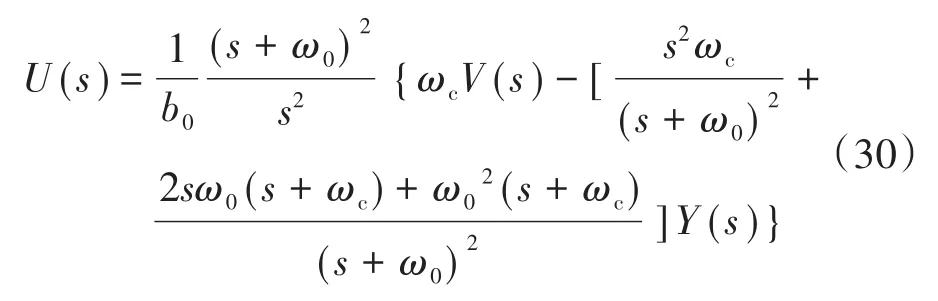
设置：

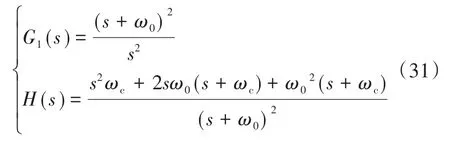
可得到简化后的结构框图，如图4所示。

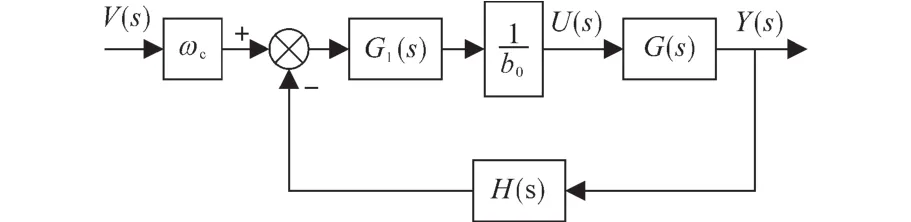
图4 系统简化框图Fig.4 Simplified block diagram of the system

系统的输出表示为

根据式（32）可知，系统的输出由输入项（V（s）项）和扰动项（F（s）项）组成。当忽略扰动项时，其控制性能仅与ωc有关，ωc越大，系统跟踪的能力越强。扰动项主要与ω0和ωc有关，直接影响了LADRC的性能[13]。取ω0=100，ωc=10，50，100，200时，频域特性曲线如图5所示。取ωc=100，ω0=10，50，100，200时，所对应的频域特性曲线如图6所示。

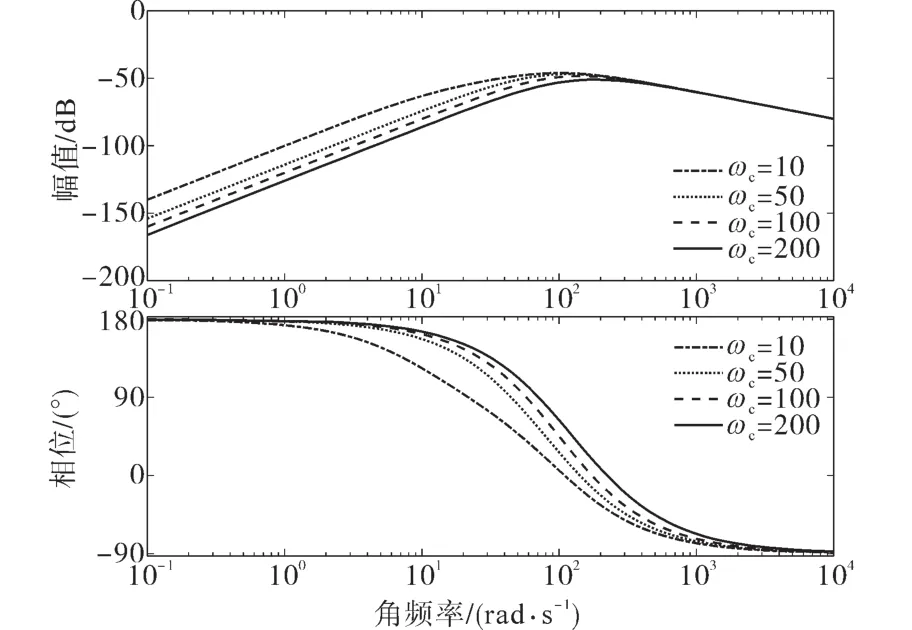
图5 输出扰动项频域变化曲线（ωc改变）Fig.5 The frequency domain variation curves of the disturbance term is output（ωcchange）

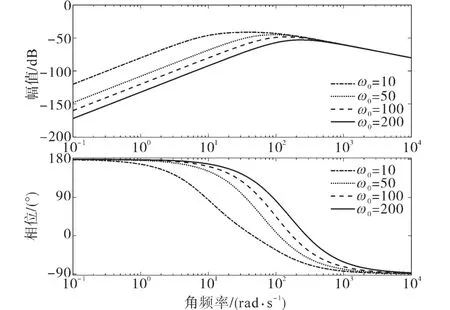
图6 输出扰动项频域变化曲线（ω0改变）Fig.6 The frequency domain variation curves of the disturbance term is output（ω0change）

根据图5、图6扰动项频域变化曲线可知，幅频特性曲线中，随着ω0和ωc的增加，中低频段扰动增益逐渐减小，高频段扰动增益基本一致；相频特性曲线中，信号的相位滞后现象也在不断减小。因此ω0和ωc的增加使得系统的抗扰性增强。

取F（s）=1∕s时，带入式（32）中扰动项可得输出响应为

经过拉普拉斯反变换得：

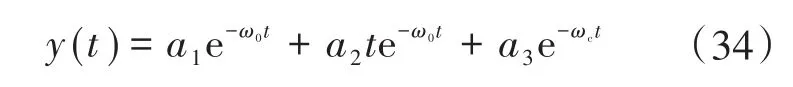
式（34）求极限后结果为零，可知在稳定状态时系统外部阶跃扰动项输出为零，也证实了改进型LADRC具有较好的抗扰性。将改进型LADRC控制与并联系统相结合，根据环流的频域模型得到系统的负反馈控制结构图，如图7所示。

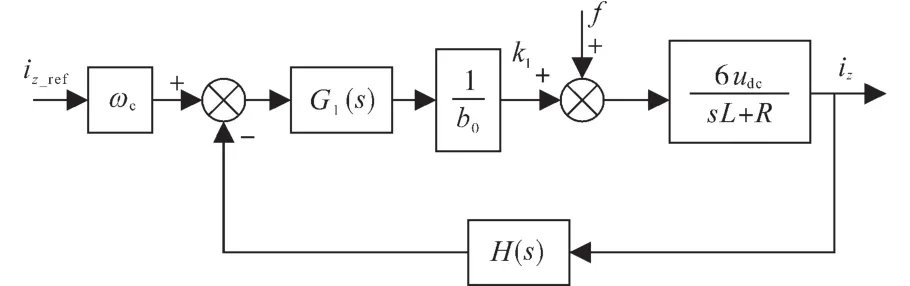
图7 负反馈控制结构图Fig.7 Negative feedback control structure drawing

根据图7可写出闭环系统的传递函数：

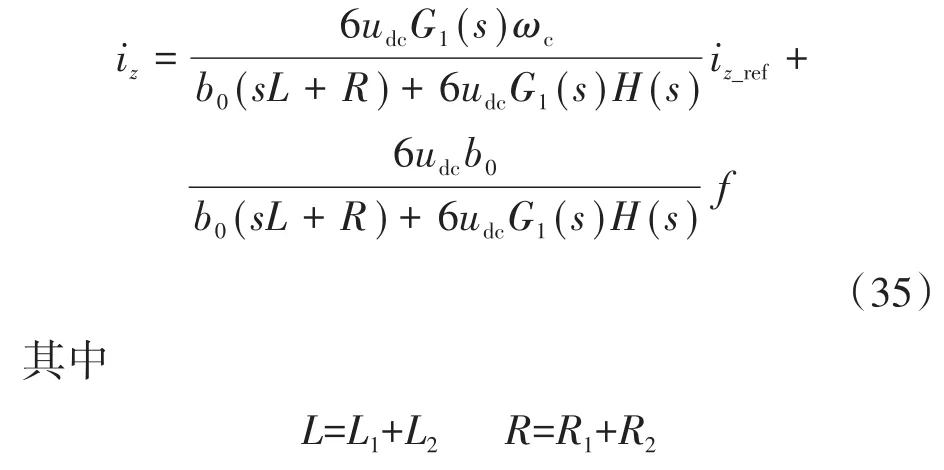
两种不同控制方法下的系统输出扰动项频域变化曲线如图8所示。中低频段改进型LADRC的扰动增益小于传统LADRC，表明了改进型LADRC抗干扰性更强。高频段两条扰动项频域变化曲线均收敛。

图8 两种控制方法的输出扰动项频域变化曲线Fig.8 The frequency domain variation curves of the output disturbance term of the two control methods

3.2 系统稳定性分析

零序环流系统输入项的传递函数为

其中

式中，ω0>0，ωc>0，udc>0，L>0，b0=6udc/L，所以式（37）中的ai>0（i=0，1，2，3，4），根据李纳德-奇帕特稳定性准则，该系统稳定的充分必要条件为

根据本文所设计的控制策略，得到两台逆变器并联系统的整体控制框图，如图9所示。两台逆变器分别由独立的控制器所控制，且控制参数相同。不同的是第二台逆变器采用传统的SVP⁃WM调制方法生成占空比，而第一台逆变器中需要对零序环流进行单独的控制，通过改进LADRC控制器生成零矢量分配因子后改变第一台逆变器零矢量占空比，使两台逆变器占空比之差为零，系统的零序环流得以抑制。

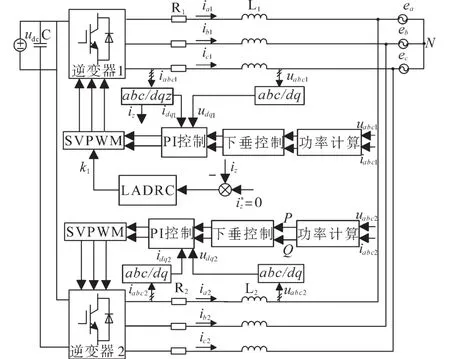
图9 基于改进型LADRC的系统控制结构图Fig.9 System control structure diagram based on improved LADRC

4 仿真对比

为了验证以上提出的改进型LADRC策略对零序环流的控制效果，基于Matlab∕Simulink平台搭建了微网逆变器并联系统仿真模型，并进行了验证。

仿真模型逆变器1、逆变器2的系统参数设置相同，设置如下：交流侧线电压380 V，额定频率50 Hz，直流侧母线电压620 V，直流侧电容器容量 1 800 μF，等效电阻 0.01 Ω。

控制器参数设置如下：比例系数kp=10，积分系数ki=128，观测器带宽ω0=150，控制器带宽ωc=800。

4.1 工况一

从理论上分析，两个并联模块的系统参数及控制参数相同时，该系统中的占空比之差应为零，开关动作一致，没有零序环流的存在。当交流侧电感值L1=L2=5 mH时，分别得出系统在没有零序环流控制、传统LADRC控制以及改进型LADRC控制下零序环流的波形，如图10所示。

图10 无控制、传统及改进LADRC控制的零序环流波形（工况一）Fig.10 ZSCC waveforms under uncontrolled，traditional and improved LADRC control（condition 1）

从图10中可以看出虽然系统参数、控制器参数均一致但系统中仍然有零序环流的存在。0.5～0.6 s期间在没有采取控制策略时，零序环流的值相对较大，峰值可达5 A。采用传统LADRC控制策略时，零序环流的峰值为1.5 A。当零序电流环采用改进型LADRC控制时，零序环流的抑制效果明显比传统LADRC的效果更好，峰值为0.24 A。

4.2 工况二

在实际的情况下，线路参数不可能完全一致，系统中存在的环流更严重，假设线路参数L1=6.3 mH，L2=5 mH时，取0.5～0.6 s期间零序环流波形，如图11所示。从图11可以看出，当线路参数差异变大时，零序环流的幅值也变大了，无控制策略的情况下，环流峰值可达到7 A。传统LADRC控制及本所提出的控制策略均有效果，采用传统LADRC控制器环流峰值为3.97 A，本文设计的控制器下零序环流可被抑制在峰值为0.72 A。

图11 无控制、传统及改进型LADRC控制的零序环流波形（工况2）Fig.11 ZSCC waveforms under uncontrolled，traditional and improved LADRC control（condition 2）

针对以上两种工况，零序环流的抑制能力对比如表1所示，可以看出改进LADRC相对于传统LADRC使零序环流下降的百分比更多，抑制能力更好。

表1 线路参数影响下零序环流抑制效果对比Tab.1 Comparison of inhibition effect of ZSCC under the influence of line parameters

4.3 工况三

以网侧电压发生跌落故障为例，验证零序环流的抑制效果。使电网侧电压从0.5～0.8 s跌落40%，可以得到并网点电压波形及零序环流变化波形，如图12所示。当电网电压下降40%时，传统LADRC控制下的零序环流在0.5～0.8 s的振荡幅度明显大于改进型LADRC控制下的零序环流，由此可知采用改进型LADRC策略对零序环流的抑制具有更好的抗干扰能力。

图12 电网电压跌落40%时传统及改进LADRC控制的零序环流Fig.12 ZSCC controlled by traditional and improved LADRC when the grid voltage drops 40%

将工况三的具体对比总结为表2，可知无论是故障前稳态时的峰值还是故障时环流的峰值，采用改进型LADRC控制策略其值均小于传统LADRC控制。并且在故障时改进型LADRC控制的零序环流上升了66.67%，相比于传统LADRC明显上升幅度更小。

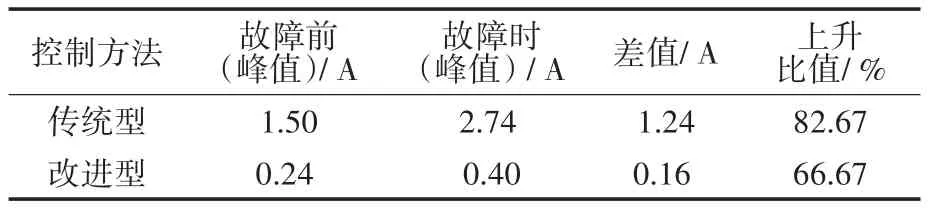
表2 电压跌落40%时两种方法控制效果对比Tab.2 Comparison of the control effects of the two methods when the voltage drop is 40%

5 结论

针对微网系统中逆变器并联时产生的零序环流问题，提出了一种基于观测误差补偿总扰动的改进型LADRC控制策略。

通过对两台PWM逆变器并联模型的分析得到零序环流数学模型，推出引起零序环流的主要原因是两台逆变器的滤波参数和占空比存在差异。为了消除这些差异，设计了改进型一阶LADRC控制器替换传统的LADRC控制器。

所提出控制策略的优点在于，针对二阶LE⁃SO观测扰动时存在的误差进行补偿，得到更准确的零矢量分配因子，调节了占空比的差异，从而有效地抑制了零序环流。

仿真结果验证了该控制策略对零序环流抑制的参考作用，同时也验证了在电网电压跌落期间该控制器具有更强的抗扰动能力。该控制策略可以扩展到N台逆变器并联系统，只需将N-1台逆变器中添加此控制器即可。但是该控制器对于系统的输出依旧存在相位滞后的问题，今后将会对这一部分进行主要研究。