基于极值理论的轨道不平顺峰值超限管理研究

何 庆，汪健辉，李晨钟，利 璐，冯晓云，王青元

(1.西南交通大学 高速铁路线路工程教育部重点实验室，四川 成都 610031；2.中铁二院华东勘察设计有限责任公司，浙江 杭州 310000；3.西南交通大学 电气工程学院，四川 成都 610031)

近年来，高速铁路的快速发展对轨道平顺性提出了新的要求。轨道平顺性对行车安全、乘坐舒适性、轨道寿命及环境噪声等具有重要影响[1]。轨道不平顺的峰值超限可能会引起列车的爬轨和脱轨，对行车安全构成极大危害[2-3]，同时也是各国现有线路养护维修常用的基本评价指标[4]。

目前，国内外诸多学者均对轨道不平顺的管理值标准进行了研究。吴旺青[5]通过分析仿真模型，提出了秦沈专线试验段轨道不平顺建议管理值；李明华等[6]建立了整车模型并求解运动方程，探索并给出时速300 km线路高低不平顺阈值；张媛等[7]基于数据分类，利用仿真数据获得不同速度等级下不平顺峰值安全域边界。以上研究对影响轨道平顺性的控制因素进行了详细分析，但针对铁路养护维修基础性工作的铁路峰值超限风险价值以及峰值管理值的合理性研究并不多见。超限风险价值VaR指在一定置信水平和未来某段时期内的最大可能损失，广泛应用于金融风险管理并正逐渐向其他行业扩展[8]。运用于铁路中是对轨道不平顺峰值超限风险价值的评估，在给定的显著水平下，线路在未来一段时间内可能出现的最大峰值。

大量研究表明，基于峰值过阈值法模型的极值理论方法在描述数据分布的尾部特征方面更具优势，侧重于关注超限数据序列分布，充分考虑了所有较大实测值出现的可能，能更客观地反映工程实际，是一种相对准确的分位数分析方法和预测工具[9-13]。针对轨道不平顺峰值超限存在低频高损、数据稀疏的特点，本文采用极值理论中的峰值过阈值法(Peaks Over Threshold)模型[14]，根据一定规则选取阈值，对历史检测值超过阈值数据进行建模，运用广义帕累托分布(Generalized Pareto Distribution)[15]研究并确定新样本序列分布函数，将既有峰值标准不同等级的容许偏差管理值视为损失值来反推超限概率P，以此来评价既有峰值管理标准的合理性。本文结合西部某高铁轨检车实测数据，对该方法的可行性和有效性进行了验证。

1 峰值过阈值法模型

与一般的模型不同，峰值过阈值法模型主要研究超过设定阈值的数据样本，观察该类序列的数值大小及总体分布特征。对于轨检车实测值序列X，假设u为阈值，超过阈值u的样本个数为nu，F(x)为分布函数。峰值过阈值法模型分析的是在X>u的条件下，超限值yi=X-u(i=1,2,…,nu)的条件分布函数Fu(y)为

Fu(y)=P(X-u≤y|X>u)y≥0

(1)

式中：P为条件概率；nu确定时y即为yi。

由式(1)可得：

(2)

将式(2)变形可得

F(x)=Fu(y)(1-F(u))+F(u)X≥u

(3)

Balkema-de Haan定理表明[12,15]，对足够大的阈值u，超限值yi近似服从于广义帕累托分布Gξ,σ(y)，则

(4)

超限值的概率密度函数gξ,σ(y)为

(5)

因此，对于给定的一个轨检车实测值序列{x1,x2,…,xn}，对数似然函数L(ξ,σ|y)可表示为

(6)

2 参数估计

由上述计算可知，对阈值u、尺度参数σ和形状参数ξ的正确估计是建立峰值过阈值法模型的关键。根据反复试验发现，阈值u的选取直接关系到能否准确估计尺度参数及形状参数。过大的阈值，会导致超限样本数量太少，从而影响分布函数的估计；过小的阈值，则无法保证超限数据的收敛性导致参数估计的偏差过大[12]。基于轨检车实测值序列的特点，本文依据超限期望图来确定阈值u[11,13]。

广义帕累托分布在形状参数ξ<1时，其超限期望函数e(m)为线性函数，可表示为

(7)

平均余值函数e(u)为

(8)

式中：nu=max{i|yi}。

由式(7)可知，若样本具有厚尾分布特征，即可认为其服从ξ<1的广义帕累托分布，则其期望余值为u的线性函数。因此，可以根据实测轨检车数据得出超限期望图，通过选取充分大的临界值u0,使得当X≥u0时e(x)为近似线性函数作为确定阈值的依据[12]。同时，可以得到轨检车实测值序列X中超过阈值的样本个数nu。

当u确定以后，利用轨检车实测值序列X，根据式(6)进行最大似然估计，即可得尺度参数σ和形状参数ξ的估计值。

3 动态不平顺峰值管理指标拟定及合理性评价

在阈值确定后，用(n-nu)/n作为F(u)的经验估计，将式(4)带入式(3)可得过阈值u的数据分布函数F(x)为

F(x)=Fu(y)(1-F(u))+F(u)=

(9)

根据上述方法求得式(9)中各参数的估计值后，即可确定过阈值u条件下分布函数。依据现有峰值管理中不同等级的管理值，利用分布函数的逆函数即可求得超限发生概率，从而实现对现有动态管理值的合理性评价。

令xm为轨检车实测值不同等级下的管理值，当x>xm,轨道动态不平顺影响舒适度、临时补修或限速，其概率P为

(10)

根据动态不平顺不同等级指标的重要性确定不同等级的发生概率Pα(即α)，一般为1%～5%。则对于给定置信水平P，可能损失值VaRP就是损失分布的P分位数，即xm的估计值为

(11)

具体拟定及评价动态不平顺峰值管理指标的流程见图1。

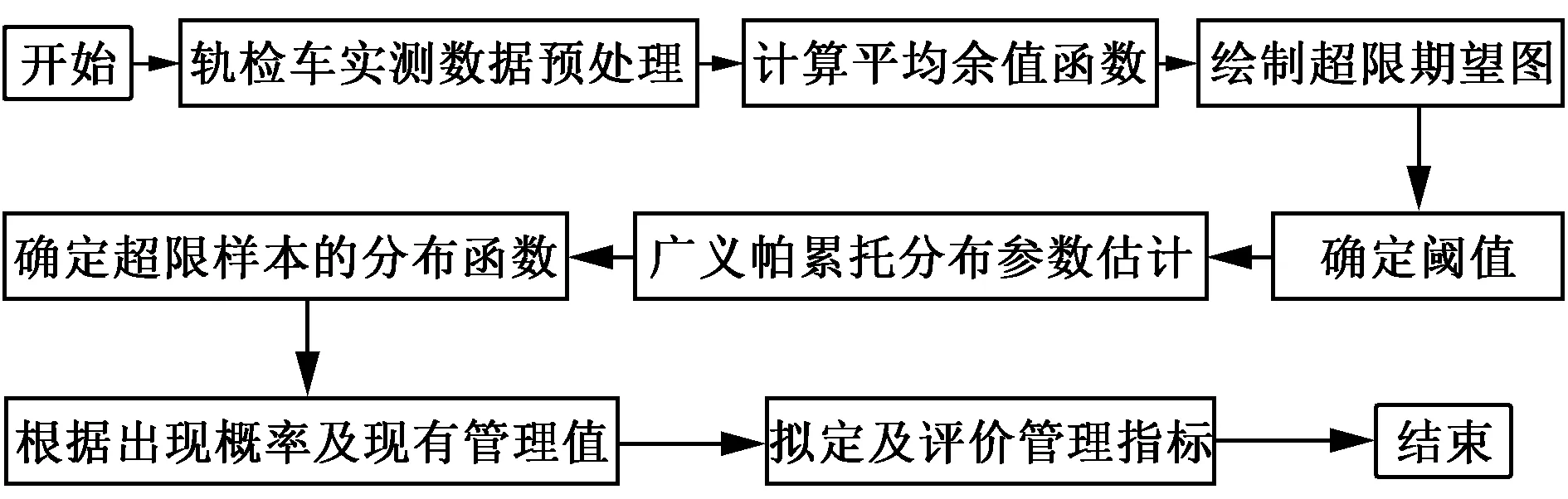
图1 拟定峰值管理不同等级指标流程

4 实例分析

以运行速度为300 km/h的某客运专线为例，选取该线上行段280 km，2016—2019年共60次轨检车实测数据进行分析，利用里程误差修正模型进行预处理[16]。

4.1 厚尾检测

以某次检测数据中高低-半峰值(绝对值)为例，绘制概率分布直方图见图2。由图2可知，该线路高低峰值分布具有明显的非正态性。通过指数分位数法进行检验，可以证实该线高低峰值分布具有相对明显的厚尾性，说明该线实际运营出现高低峰值的概率较正态分布出现的概率要大。因此，通过极值理论建立峰值过阈值法模型计算风险概率，针对厚尾分布进行重点分析。

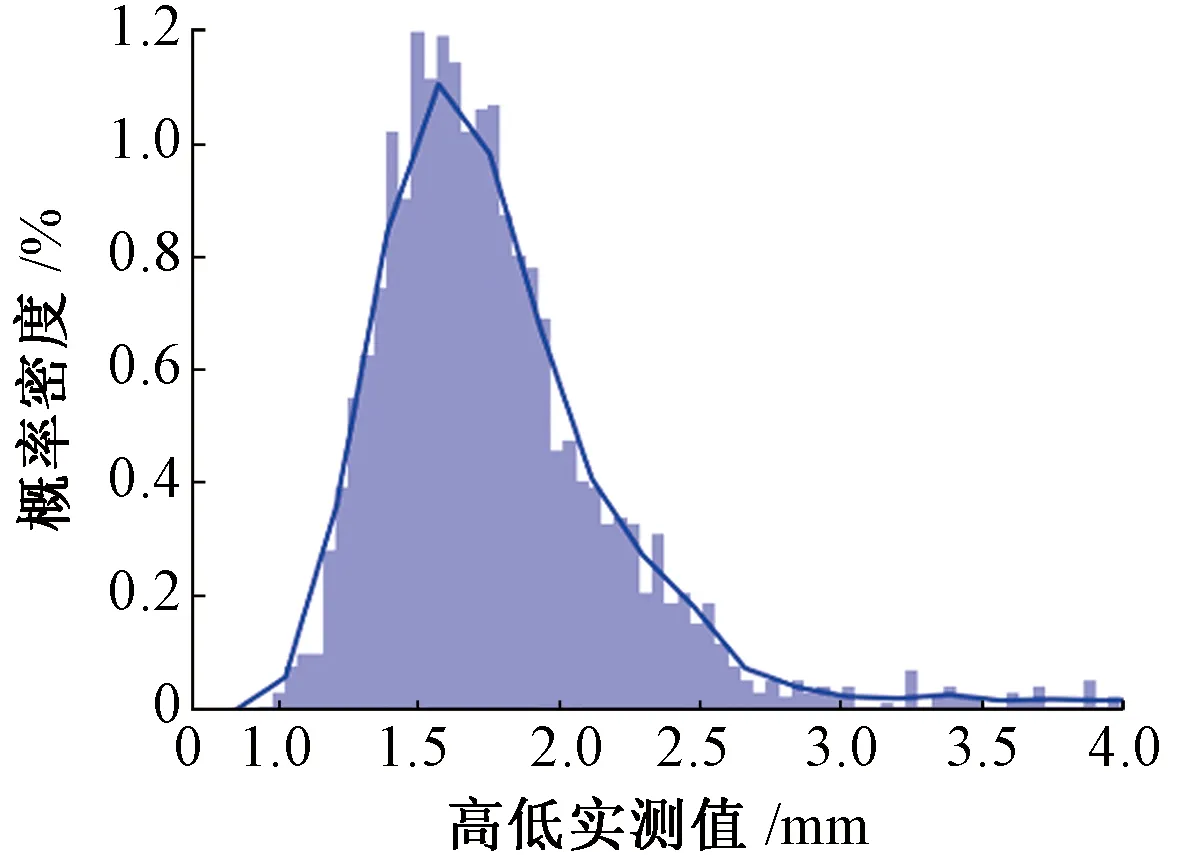
图2 高低实测值概率分布直方图

4.2 阈值讨论及参数估计

以高低-半峰值(绝对值)为例，根据式(8)计算样本平均余值函数，绘制图3所示超限期望图。一般而言，合适的阈值u能够将10%左右的数据划分为超限样本，否则无法抓住序列分布的特征[12]。经过多次试验验证，选取7 km为一个区间进行划分较为合理，由此可得4 800个轨检车高低-实测半峰值序列。由图3可以看出，当阈值u在3 mm附近，余值函数e(u)变化幅度较小为近似线性函数且斜率有正向变大的趋势，说明超限数据较正态分布的尾部要厚，适用于帕累托模型进行厚尾的分布拟合以描述尾部的特征。此时，只有少量的高低实测值点分布在图2的尾部，且收敛速度缓慢，符合帕累托分布的特征。利用余值函数即可初步判定该观测值为所需阈值u[17],此时过阈值u=3 mm的样本个数nu为387，占比约为8%。由此可以推断阈值为3时比较合适。也允许适当放宽该线左高低峰值Ⅰ级管理值，不妨取u=4、u=5并与u=3进行对比见图4和图5。利用最大似然估计，分别计算三种不同阈值情况下的尺度参数和形状参数估计值及对应的累计分布函数和风险价值见表1。

表1 不同阈值下的累积分布函数F(x)和风险价值函数VaRP

图3 高低实测值序列超限期望

图4 不同阈值下的累计分布函数

图5 不同阈值下的风险价值函数

由图4可知，阈值u=3比u=4、u=5的累计分布函数F(x)包含更多的超限阈值概率，使得估计的参数更准确。由图5可知，尽管不同阈值在低显著水平(P<90%)下，相同的显著水平各自的风险价值不同，但当显著水平较高时(P≥90%)相同的显著水平、不同的阈值对应的风险价值十分相近。因此，从严谨的角度出发，本文选取阈值u=3 mm科学合理。而对于动态不平顺水平这一项指标，规范中Ⅰ级管理值为5，大于其余同级别各指标。作如上相同分析后发现水平阈值取4更为合理。

4.3 峰值管理值的拟定及评价

确定阈值后，在高低-半峰值的偏差等级为Ⅰ级(经常保养)超限概率为5%的情况下，对超阈值样本使用广义帕累托分布求得的Ⅰ级管理值指标为4.4 mm，与文献[18]中250(含)～350 km/h线路轨道动态质量容许偏差管理值的4 mm相近。结合式(11)可以反推出该线路出现高低峰值偏差为等级Ⅰ级时的概率为5.85%，出现Ⅱ级(舒适度)的概率为3.14%，出现Ⅲ级(临时补修)的概率为1.72%，而出现Ⅳ级(限速(160 km/h))的概率为0.55%。对其余几项指标做相同处理，分别可得各自阈值、尺度参数、形状参数及不同等级下的超限概率见表2和表3。

表2 不同指标的阈值及参数估计值

表3 某运营速度300 km/h线路不同指标峰值超限概率 %

由表2和表3可得，对于该客运专线，轨向的动态质量容许偏差管理值相对宽松，超过9%的概率需要经常保养，更有约5%的概率需要限速，可以考虑根据规范适当提高标准；轨距的Ⅱ级及以上峰值管理值相对严格，均只有小于1%的概率，可以考虑根据规范适当放宽标准；其余指标水平、扭曲和高低的峰值管理值相对合理，可以根据现场实际情况，适当调整。

4.4 加速度分析

峰值管理还包含车体垂向、横向加速度的等级划分，见表4。然而根据实际现场养护维修调查发现，加速度检测值往往小于Ⅰ级标准，而达不到检修的目的。因此，本文对已有垂向、横向的现场加速度检测值按照时间序列做箱形图分析，结果见图6。

表4 250(不含)～350 km/h 线路轨道动态质量容许偏差管理值

图6 加速度实测值箱形图

由图6可知，垂向加速度的范围在(-0.04～0.04)g内，横向加速度的范围在(-0.03～0.03)g内，均未有检测值超过规范中的Ⅰ级标准。这说明现场养护维修作业时，峰值管理中的加速度指标并没有起到很好的限制效果[19-20]。由于本文采用的基于极值理论的峰值过阈值法模型有其特定的应用范围，只适用于描述及分析过阈值数据的广义帕累托分布特征，不必对数据序列总体的分布类型进行建模。

由于该线路不同检测时间下的加速度实测值均未有超限的情况出现，这也意味着此模型不适用于该线路既有加速度管理值的合理性评估。因此，需要根据现场实际情况，适当的将现有峰值管理中的加速度指标严格化以达到实际的养护维修参考标准。

5 结论

本文基于峰值过阈值法模型，借助广义帕累托分布函数，研究轨道动态不平顺峰值管理值的合理性，结合轨检车实测数据进行验证分析。以下结论是对模型优缺点及现有峰值管理指标合理性的总结：

(1)轨道动态不平顺峰值管理值的拟定及评估本质上考虑的是极端事件。峰值过阈值法模型采用阈值的划分特点，只分析过阈值样本的广义帕累托分布特征，根据既有规范，计算不同等级VaRP的超限概率，实现对峰值管理标准的合理性评价。该方法充分考虑了可能出现的轨道动态不平顺较大实测值，更全面的体现了实测数据的分布特征，得到的超限概率能更客观的反映工程实际。

(2)根据实测数据分析可得，该线轨向及车体垂向、横向加速度动态质量容许偏差管理值较宽松，约高于实测峰值的50%，可以考虑根据规范及现场实际情况适当提高标准；轨向管理值相对宽松，约10%的实测峰值超限，其中，Ⅳ级限速标准的超限概率约5%，不符合实际线路运营需求，应根据实际情况适当提高容许偏差管理值，从而达到降低超限概率的目的；轨距Ⅱ级及以上峰值管理值相对严格，超限概率均小于1%，可以考虑适当放宽标准；其余指标水平、高低及三角坑的峰值管理值相对合理，可以根据现场实际情况进行适当调整。

(3)本文为简化分析，仅考虑其数值大小，未考虑阈值的时间维度，且根据超限值出现的概率评定管理值的合理性具有一定经验性。为了更加客观描述峰值管理值的合理性，是今后需要重点研究的问题。