电传动装甲车辆负载功率预测实时能量管理策略*

陈路明，廖自力，魏曙光，张 征

(陆军装甲兵学院 兵器与控制系, 北京 100072)

传统装甲车辆多采用机械传动方案，即以发动机作为原动机，通过机械传动装置将功率流传递到末端车轮，驱动车辆行驶。这种结构方案路径简单、可靠性高且技术成熟，在装甲车辆中得到广泛应用[1]。但是随着新军事变革的不断推进，传统机械结构在机动、防护、火力以及油耗等方面逐步接近极限，制约了战斗力的跃升。电传动方案具有无级变速、低速大扭矩、电压和功率等级高、柔性布线便捷以及节能减排等优点，成为未来装甲车辆的重要发展方向[2]。

电传动装甲车辆通常包含两种以上动力源，通过控制电能产生、变换、传输和存储等过程，赋予整车多电压和多功率等级供电能力。由于不同动力源工作特性差异较大，如何根据负载功率需求，协调控制多动力源输出成为制约电传动车辆性能发挥的关键。文献[3]采用小波变换和模糊控制相结合的方法，对电传动装甲车辆中多动力源进行功率分流，提升了系统工作效率。文献[4]针对未来战斗车辆，提出了一种基于神经网络和模糊控制的混合动力系统能量管理策略，增强了车辆对工况的适应性。文献[5]对比了多种串联式装甲车辆系统结构方案，制定了固定规则的功率分配策略，仿真验证了可行性。然而，上述研究主要以当前时刻负载功率为参考，下达控制指令时车辆实际状态已发生改变，导致控制作用滞后。由于电传动装甲车辆大多工作在复杂非道路工况，路面特征无法通过全球定位系统(global positioning system, GPS)等传统外部信号源预先获取，而国内外关于装甲车辆工况预测的研究鲜有报道，迫切需要开展针对性研究工作。

因此，本文以8×8轮式电传动装甲车辆为研究对象，提出一种具有负载功率预测功能的实时能量管理策略，并采用仿真方法验证所提控制策略的可行性。

1 电传动系统建模与控制方案设计

1.1 系统结构分析

根据动力流路径，串联式电传动装甲车辆可分为前功率链和后功率链，图1给出了8×8轮式电传动装甲车辆结构。其中，前功率链为发动机-发电机组、动力电池组和超级电容组，后功率链为8个轮毂驱动电机以及若干辅助用电设备。

图1 车辆电传动系统结构Fig.1 Structure of vehicle electric drive system

1.2 系统动力源建模

1.2.1 发动机模型

(1)

其中，Te为实际转矩，ne为实际转速，κ1和κ2分别为转矩和转速的纯滞后延时，τ1和τ2分别为转矩和转速的惯性时间常数。

发动机曲轴端的机械输出功率为：

(2)

由发动机万有特性曲线可知，发动机的燃油消耗率由转矩和转速唯一确定，即

(3)

为便于积分计算，将式(3)进行单位变换。

(4)

1.2.2 发电机模型

由发电机map图可知，发电机工作效率与转速和转矩相关，即

ηg=gmap(Tg,ng)

(5)

式中，ηg为发电机工作效率，gmap为效率关于实际转矩和实际转速的二维拟合曲面函数，Tg为实际转矩，ng为实际转速。

发动机机械动力输出轴与发电机转子轴采用刚性方式连接，二者转速相同，可用式(1)中定义的发动机实际转速替代发电机实际转速，则发电机的目标转矩为：

(6)

发电机转矩响应迅速，忽略延时对精度影响不显著，该动态过程可等效为小惯性环节[7]，即

(7)

将式(6)、式(7)代入式(5)，化简得：

(8)

式中，gmap1为发电机效率关于目标功率和实际转速的二维拟合曲面函数。

1.2.3 动力电池模型

动力电池采用等效电路模型，电流关系为：

Ebat-IbatRbat-Ubat=0

(9)

式中，Ebat为电池开路电压，Ibat为电池电流，Rbat为电池内阻，Ubat为电池端电压。

式(9)两边同乘电流，得功率平衡方程[8]

(10)

式中，Pbat为电池输出功率。

电池荷电状态(state of charge, SOC)定义为：

(11)

式中，Sbat为电池荷电状态，Qrem为初始时刻剩余容量，Qused为t时段内消耗容量，Qfull为额定容量。

将式(10)和(11)联立，并求导可得：

(12)

1.2.4 双向DC/DC模型

双向DC/DC可对直流电压进行等级变换，具有Boost和Buck两种模式[9]。在Boost模式下从电池吸收电能释放到直流母线，在Buck模式下从母线吸收电能存储到电池，电压关系为：

(13)

式中，Uin为输入侧电压，Uout为输出侧电压，α为导通占空比。

由于存在效率损失，变换前后电流关系为：

(14)

式中，Iin为输入侧电流，Iout为输出侧电流，ηdc为DC/DC工作效率。

由试验数据可知，DC/DC工作效率由输出功率决定，对二者进行多项式拟合，可得：

ηdc=hdc(Pdc)

(15)

式中，hdc为DC/DC效率关于输出功率的一维拟合曲线函数，Pdc为DC/DC输出功率。

1.2.5 超级电容模型

超级电容的功率平衡方程为

(16)

由于存在内阻损耗，实际输出功率Psc为

(17)

式中，ηsc为超级电容工作效率。

超级电容的工作效率与输出功率有关，可由实际采样数据通过多项式拟合得到。

ηsc=δsc(Psc)

(18)

式中，δsc为效率关于功率的一维拟合曲线函数。

1.3 能量管理控制方案

非线性模型预测控制(nonlinear model predictive control, NMPC)通常将预测时域内的P步扰动变量视为定值，但实际扰动变量是持续变化的，简单定值化处理势必降低控制精度[10]。为此，本文利用非平稳负载功率组合预测方法预测未来P步的负载功率变化，作为NMPC参考扰动变量信号，在有限时域内在线滚动优化求解，确定最优控制量。能量管理方案如图2所示。

图2 能量管理控制方案Fig.2 Energy management control scheme

2 非平稳负载功率组合预测方法设计

2.1 差分自回归移动平均模型预测方法

差分自回归移动平均模型(auto regressive integrated moving average model, ARIMA)能够利用历史数据进行统计分析，消除随机波动的影响，适用于短期和超短期预测[11]。

2.1.1 差分处理

设非平稳趋势性观测样本为X1,X2,…,Xn，经d阶后向差分后，得到平稳序列

▽dXk=(1-B)dXk=Wkk=d+1,…,n

(19)

式中，▽d为d阶差分算子，B为线性滞后算子，Xk为非平稳时间序列，Wk为平稳时间序列。

Wk满足条件

φ(B)(Wk-μ)=θ(B)εk

(20)

2.1.2 模型定阶

根据截尾性确定模型阶数，可得：

(21)

(22)

依据赤池准则，确定阶数p和q的值，即

(23)

2.1.3 参数估计

ARIMA模型参数p和q采用极大似然估计方法通过迭代方式计算得到，似然函数为：

(24)

式中，Γn=E(WnW′n)。

2.1.4 多步预测

对平稳序列Wk复原得到非平稳序列Xk。

(25)

2.2 自适应马尔可夫链预测方法

马尔可夫链适用于预测平稳随机序列，可在线更新状态转移矩阵状态。

2.2.1 状态栅格化处理

若变量论域范围为[Xmin,Xmax]，根据预测精度和硬件能力，对论域进行栅格化处理。

(26)

式中，Si为第i个栅格状态，r为栅格数量。

采用最近邻域法对N个样本数据进行分类。

(27)

2.2.2 窗口状态转移矩阵计算

截取临近N个样本历史数据，计算该窗口空间内由状态Si转移到Sj的概率pij。

(28)

式中，Mij为由栅格状态Si转移到Sj的次数。

因此，可得第i个窗口的状态转移矩阵Pi为：

(29)

2.2.3 自适应更新状态转移矩阵

为实现多场景在线应用，采用遗忘因子方法，对历史数据赋予不同权重系数，以消除数据饱和现象，加强当前数据的影响[12]。

采用线性递减方式，设置遗忘因子权重系数。

(30)

式中，ρi为第i个窗口状态转移矩阵的权重系数，γ为历史记录的窗口状态转移矩阵数量。

(31)

该状态转移矩阵估计值的展开式为：

(32)

2.2.4 一步预测

若当前时刻的栅格状态为Si，根据状态转移矩阵估计值，对下一时刻状态进行一步预测。

(33)

式中，jmax为预测下一时刻的栅格状态标号，arg max为使公式达到最大值时变量j的取值。

对栅格状态进行清晰化处理，可得：

(34)

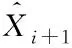
2.3 组合功率预测方法设计

为提高预测精度，发挥不同预测方法的优势，利用ARIMA进行平稳趋势性预测，利用马尔可夫链进行非稳态残差预测，构建组合预测方法，原理结构如图3所示。

图3 组合功率预测方法Fig.3 Joint power prediction method

3 非线性模型预测控制方案设计

非线性模型预测控制是一种起源于工业控制领域的先进控制方法，可为车辆的实时优化过程提供可靠的控制框架[13]。

3.1 非线性预测模型

联立式(4)和式(8)，可得发动机-发电机组的油耗优化项为：

(35)

式中，ζ为[t0,tk]时间段内的发动机燃油消耗体积，Peg为发动机-发电机组输出到直流母线的功率。

联立式(12)和式(15)，可得动力电池和双向DC/DC的SOC优化项为：

(36)

其中，Pbd为动力电池和双向DC/DC输出到直流母线的功率。

联立式(16)和式(17)，可得直流母线电压的优化项为

(37)

其中，Usc0为初始t0时刻直流母线电压值。

根据前后功率链平衡关系可得：

Preq=Peg+Pbd+Psc

(38)

式中，Preq为各类负载由直流母线吸收的功率。

据此，可以得到非线性预测模型表达式。

(39)

其中，x、u、v和y分别为状态向量、控制向量、扰动量和输出向量，各自展开式分别为[ζ，Sbat，Usc]T、[Peg，Pbd]T、Preq和[ζ，Sbat，Usc]T。

在稳态工作点邻域内进行泰勒级数展开，忽略二次以上高阶项，得到线性化模型[14]。

(40)

其中，A、B1、B2和C分别为3×3维的状态系数矩阵、3×2维的控制系数矩阵、3×1维的扰动系数矩阵、3×3维的单位输出系数矩阵。

为便于计算机应用，对线性化模型进行精确离散化处理，可得：

(41)

其中，G、H1和H2分别为3×3维离散状态系数矩阵，3×2维离散控制系数矩阵，3×1维离散扰动系数矩阵。

3.2 在线滚动优化

在有限时域内，建立关于发动机油耗、直流母线电压和动力电池SOC的多目标优化函数。

(42)

式中，Uref和Sbat,ref分别为直流母线电压和动力电池SOC的期望值，P为预测时域长度，α1、α2和α3分别为体现驾驶员操作意图的优化权重系数。当发动机油耗的权重系数调大时，发动机趋向在高效区域平稳变化，功率响应速度较慢，为维持前后功率链平衡，动力电池频繁充放电，SOC稳定效果变差，甚至当需求功率变化幅度超过电池能力范围后，会造成母线电压的大幅波动；同理，当直流母线电压或动力电池SOC的权重系数改变时，也会影响其他优化项的输出效果，α1、α2和α3通过仿真获得，分别取0.6、0.5、0.3。

为降低计算开支，假设M(M

(43)

(44)

在单计算周期内，仅将最优控制序列首个元素施加到系统，并在下一个时刻重复上述过程。

3.3 误差反馈校正

由于存在扰动和时变，预测模型与实际装置不可能完全一致。而在线滚动优化本质属于有限时域的开环控制，无法解决误差累加问题。为此，引入误差反馈校正环节，将总和误差反馈到系统，以实现系统闭环无偏差跟踪[16]。

若当前时刻预测误差为：

(45)

假设下一时刻预测时域内各变量误差不变。

(46)

4 仿真实验与结果分析

本文采用硬件在环仿真平台对所提的实时能量管理策略进行验证。硬件在环仿真实验能够真实模拟数据交互过程，极大缩短控制算法开发周期，降低安全风险和经济成本。该硬件在环仿真平台结构如图4所示。

图4 硬件在环仿真平台Fig.4 Hardware-in-loop simulation platform

平台包括控制系统、驾驶员操纵系统、动力学实时仿真系统、车载综合电力系统以及高压低压负载系统5部分，其中驾驶员操控系统通过串口通信分别与控制系统和动力学实时仿真系统相连，其余4个系统通过Flexray总线进行数据交互。能量管理算法以代码形式下载到DSP中央控制器中，对整车进行实时控制。

车辆参数和控制参数如表1所示。由于当前尚无针对电传动装甲车辆的标准测试工况，选取相同控制参数的无预测模型预测控制作为基准，在两种典型路面进行仿真实验。

4.1 水泥路面行驶工况

车辆初始时刻为静止状态，母线电压和电池SOC分别为750 V和60%，在驾驶员加速、转向以及制动等操控指令下的仿真结果如图5所示。

由图5(a)驾驶信号可知，车辆在2～18 s进行快速加减速直线行驶，最高车速为54.14 km/h，最大加速度为4.05 m/s2；在21～62 s进行缓慢加减速直线行驶，最高车速达到83.16 km/h；车辆在67～139 s进行中低速蛇形转向，最高车速不超过52.56 km/h；在145～166 s方向盘向右打满，车辆进行小半径原地转向；在180～230 s进行高速行进间蛇形转向，最高车速达到62.28 km/h；其他时间车辆为静止状态。

(a) 驾驶员操控指令(a) Driver control instructions

图5(b)所示的负载功率变化曲线表明，整个行驶过程中负载功率呈现非平稳趋势性变化特征，单一ARIMA预测方法对于平稳趋势性变化预测较为准确，但在非平稳功率预测时出现较大跳变，预测精度较低；组合预测方法能够以较高精度预测负载非平稳趋势性功率变化，最大偏差不超过20 kW，验证了组合方法在提升非平稳趋势性功率预测精度方面的有效性。

对比图5(c)和图5(d)功率分配结果可以看出，相较于无预测控制，有预测控制中发动机-发电机组频繁参与功率调节过程，动力电池通过更加快速的充放电优化发动机工作状态，超级电容瞬时最大充放电功率减小了100 kW，表明负载功率预测环节能够为优化控制环节预先提供有价值的参考信息，提升了多动力源协调控制水平。

根据图5(e)和图5(f)可知，无、有预测控制的直流母线电压波动范围分别为69.23 V和44.67 V，电池SOC波动范围分别为6.34 %和4.32 %，这证明了有预测控制在并行优化多个指标方面的优势。图5(g)和图5(h)分别为无、有预测控制条件下的发动机工作点分布，可以看出无预测控制中发动机工作点分布较为分散，部分工作点偏离最佳油耗曲线较远，而有预测控制中发动机工作点较为集中地分布在最佳油耗曲线附近，且在1 200～1 800 r/min以及1 000～1 700 N·m的高效区间内分布比例更大。这体现了有预测控制在优化发动机工作状态，提升燃油经济性方面的突出效果。

4.2 冰雪路面行驶工况

车辆在冰雪路面行驶工况下的初始状态与水泥路面行驶工况设置相同，在驾驶员加速、转向以及制动等操控指令下的仿真结果如图6所示。

图6(a)为车辆在冰雪路面行驶的驾驶信号及车速信息，车辆在2～20 s进行快速加减速直线行驶，由于路面附着系数较低，车轮存在滑转，最高车速为52.56 km/h，最大加速度为3.32 m/s2，均低于水泥路面行驶效果；在24～58 s进行缓慢加减速直线行驶，最高车速达到72.36 km/h；在62～120 s进行中低速蛇形转向，最高车速不超过32.04 km/h；在135～151 s方向盘向左打满，进行小半径原地转向；车辆在161～211 s进行行进间高速蛇形转向，最高车速达到60.84 km/h；其他时间车辆为静止状态。

(a) 驾驶员操控指令(a) Driver control instructions

根据图6(b)可知，单一ARIMA预测方法非平稳功率预测精度较低，最大误差达到110 kW，而组合预测方法能够有效应对非平稳变化过程，最大预测误差不超过30 kW，证明了组合预测方法对非平稳趋势性功率预测的有效性。

图6(c)和图6(d)分别为无、有功率预测的功率分配结果，可以看出，相较于无预测控制，有预测控制下发动机-发电机组功率输出更加平稳，负载功率变化时动力电池介入调节工作更早，超级电容功率波动幅值和频率显著降低，证明了预测环节对于预先调节动力源工作状态的提升效果。

通过对比图6(e)和图6(f)直流母线电压和电池SOC变化可知，无、有预测控制的直流母线电压波动范围分别为108.21 V和61.58 V，电池SOC波动范围分别为4.47 %和3.86 %，这证明了有预测控制在并行优化多个指标方面的优势。由图6(g)和图6(h)可知，无预测控制中发动机工作点分布较为分散，尤其在1 000～1 400 r/min转速区间部分工作点偏离最佳油耗曲线较远，而有预测控制中发动机工作点集中地分布在最佳油耗曲线附近，仅有少量工作点偏离较远。这体现了有预测控制在优化发动机工作状态，提升燃油经济性方面的突出效果。

5 结论

论文以8×8轮式电传动装甲车辆为研究对象，分析了电传动装甲车辆的电功率耦合结构特点和发动机、发电机等关键部件特性，提出了一种具有负载功率预测功能的实时能量管理策略，并进行硬件在环仿真验证，具体结论如下：

1) 针对负载功率呈现的非平稳趋势性变化特点，提出了ARIMA和马尔可夫链的组合预测方法，分别对平稳趋势性变化的主体部分和非平稳无趋势性变化的残差部分进行预测，提高了对负载功率的预测精度。

2) 以非线性预测模型控制方法为框架，构建了降低发动机油耗、稳定母线电压以及电池SOC的多目标优化函数，并采用序列二次规划法进行在线滚动求解，将最优控制序列首个元素应用于被控对象，有效提升了车辆能量管理水平。

3) 依托硬件在环实时仿真平台，分别在水泥、冰雪两种典型路面上，设计了高、低速直驶与转向联合工况实验，对基于负载功率预测的实时能量管理策略进行验证。结果表明，相比于传统无功率预测的非线性模型预测控制方法，所提控制方法显著提升了母线电压和电池SOC稳定精度，优化了发动机燃油经济性，为基于模型预测控制的工程应用提供一个新的思路。