围压下固体推进剂的破坏机理分析*

张 亮，申志彬，虞跨海

(1. 河南科技大学 土木工程学院， 河南 洛阳 471023； 2. 国防科技大学 空天科学学院， 湖南 长沙 410073)

固体发动机作为导弹或者运载火箭的动力装置，通常采用发动机点火试验来考核其结构完整性。固体推进剂不仅对应变率和温度变化非常敏感，同样也对压力极为敏感。以贴壁浇筑的圆管形装药固体发动机为例，在发动机点火状态下推进剂处于三向围压状态，在点火状态下推进剂药柱的环向、径向和轴向三个方向均承受压应力，此时推进剂药柱的环向受到压力载荷作用而在壳体边界推进剂的形变受约束，在挤压作用下推进剂药柱的环向承受拉应变。如果采用单轴拉伸试验考核推进剂的力学性能，推进剂的加载本质上来说其实是围压下的拉伸过程。研究推进剂在围压下的力学响应对于理解推进剂在超常环境下的力学行为具有极其重要的意义。

针对发动机在点火增压过程中推进剂承受的围压载荷可能会引起其力学行为变化的问题，在20世纪中期就引起了国外一些学者的注意。Lindsey等[1]通过将Instron拉伸机置于一个充满气体或者液体的密闭容器内进行单轴拉伸来给黏弹性材料施加一个三轴的拉压应力场，但是文中并没有给出具体的试验方法。Traissac等[2]在围压从环境压强到15 MPa变化时开展了复合推进剂的单轴拉伸试验，发现随着围压的增大，推进剂的失效应力和失效应变都显著增加，但是推进剂的力学性能参数不会总是随着围压的增大而持续增加，而是存在一个饱和压强使参数趋于一个稳定值。Özüpek和Becker[3]根据围压下推进剂的力学特性共同提出了考虑围压的推进剂本构模型，后续的一些学者对该本构模型进行了改进[4]、数值离散[5]，或考虑了大变形和损伤[6-7]，或将其与老化的评估相关联[8]。张建彬[9]通过自研的油压式围压加载试验装置[10]以单轴定速压缩的试验形式研究了双基推进剂的力学响应与围压的关系。何铁山和张劲民[11]发现高能硝酸酯增塑聚醚(nitrate ester plasticized polyether propellant, NEPE)推进剂的拉伸强度和最大延伸率均随着围压载荷的增加而增大。王广和陈刚[12]发现围压可以提升推进剂的抗拉强度，改善其力学性能。沙宝林和侯晓[13]建立了推进剂考虑围压的含损伤本构方程。姚东等[14]基于广义回归神经网络对围压下NEPE推进剂的力学强度参数进行预测。王小英等[15]与Traissac等[2]的发现类似，认为随着围压载荷的持续增大，推进剂的强度和延伸率在提升的过程中存在一个阈值。刘梅等[16]提出在围压下以推进剂的断裂伸长率为发动机点火状态下的破坏判据更为合理。申志彬等[17]开发研制了气压式围压加载试验系统，通过围压下的单轴拉伸试验研究推进剂围压相关力学性能。

目前针对围压下推进剂力学性能的研究大部分还处于唯象阶段，需要机理层面的进一步探究。借助细观损伤模型研究推进剂的损伤破坏机理是一条行之有效的途径，推进剂内部各组分之间界面的失效可以通过内聚力模型来定义，Hillerborg等[18]在研究混凝土中裂纹的形成和扩展时提出了双线性内聚力模型，其物理意义非常清晰且形式简单，是目前应用最广泛的内聚力模型之一。南京理工大学的周长省教授团队基于指数型内聚力模型研究了基体松弛特性[19]和基体初始缺陷[20]对复合推进剂力学性能的影响，并通过分段函数式内聚力模型模拟复合推进剂[21]和双基推进剂[22]的界面“脱湿”和基体中的裂纹扩展问题。推进剂的损伤破坏机理研究通常借助细观和微观试验手段，如采用扫描电镜观察推进剂裂纹尖端的动态损伤[23]、界面的裂纹演化[24-25]和颗粒的破碎情况[26]。

本文从高固体含量复合推进剂在不同的温度、应变率和围压下的单轴定速拉伸试验入手，通过推进剂在围压下的力学响应特征，借鉴分子动力学思想，基于有限元方法和内聚力模型建立了推进剂的细观有限元计算模型，对推进剂在围压下的损伤和破坏过程进行了仿真计算，并通过电镜扫描试验对推进剂试样的断面形貌进行了深入分析，通过仿真结合试验的手段研究了围压下固体推进剂的损伤破坏机理。

1 试验方案和试验结果

自研的气压式围压加载试验系统原理如图1所示。该系统配置的单轴拉伸加载模块最大加载的载荷是1 000 N，夹头的最大行程为150 mm，最大拉伸速率是6 000 mm/min，最大加载围压可以达到15 MPa，加载过程中温度变化范围从低温-80 ℃到高温+180 ℃，夹头在运动过程中可以通过围压加载装置实现不同温度、压力和应变率的加载。加载过程中两个试件同时安装在试验机两个对称的夹头上，通过一次拉伸试验可以得到两组试验数据，避免由于试样本身的问题而导致无法在拉伸试验中获得任何数据。

图1 围压加载试验系统原理Fig.1 Schematic diagram of superimposed pressure loading system

1.1 试验方案和试验过程

试验采用质量分数为88%的复合推进剂，其中AP和Al的质量分数分别为70%和18%。试验采用标准的哑铃型试件，如图2所示，试件的长度为120 mm，拉伸标距为70 mm。

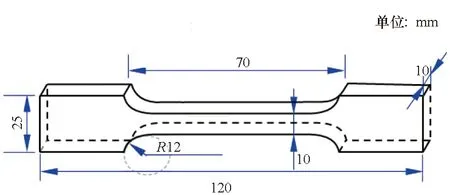
图2 推进剂哑铃型试件示意图Fig.2 Schematic diagram of dumbbell type specimen of solid propellant

该试验方案是在GJB770B-2005推进剂试验方法的基础上针对空空导弹试验的特殊要求设计的。试验选取高(70 ℃)、低(-50 ℃)、常温(23 ℃)三个特征温度，选取高(1 000 mm/min)、低(100 mm/min)两个特征拉伸速率和从常压到8 MPa围压的3～4个环境压力。每种工况都至少做2个平行试样。

试验前首先启动空压机(如图1所示)，空压机通过连接管与储气罐进行连接，根据试验的要求将空压机产生的高压气体经由连接管存储到储气罐中。对储气罐的压力进行实时监控，确保压力达到试验要求并且在安全范围。在试验过程中，储气罐中的高压气体通过与储气罐连接的压力控制器控制阀门开合进入围压舱中。在高温(+70 ℃)和低温(-50 ℃)试验中，围压舱置于高低温试验箱内部，通过温控模块来控制围压舱内的温度达到试验要求。围压试验结束后，借助龙门起吊机挂在围压舱上方的吊耳将围压罩吊起，完成试样的更换。单轴加载装置位于围压舱内，加载速率由电机的输出扭矩控制，实现推进剂试样在不同拉伸速率下的加载。试验结束后，推进剂在围压下的拉伸曲线是力-位移曲线，需要将其处理为应力-应变曲线。

1.2 试验结果

在常温下，当围压载荷在常压和8 MPa之间变化时，推进剂在两个拉伸速率下的应力-应变响应曲线如图3所示。在相同的应变率下，初始模量受围压的影响不大，无论有无围压加载，应力-应变曲线在“脱湿”点之前基本重合。而在“脱湿”点之后，围压显著提升了推进剂的刚度和强度。当拉伸速率较小(100 mm/min)时围压对伸长率的影响很小，但是随着拉伸速率的提高，在围压下推进剂的伸长率显著下降。当拉伸速率达到1 000 mm/min时，施加8 MPa围压后推进剂的最大伸长率比常压时下降接近50%。Özüpek[3]在其论文中描述的现象与本研究的发现有所不同，在围压下推进剂的强度和伸长率均随着拉伸速率的增加而增大。初步推测其原因是本研究使用的端羟基聚丁二烯(hydroxyl terminated polybutadiene propellant, HTPB)推进剂固体含量高于NEPE。此外，本研究在试验中采用的拉伸速率也更高。

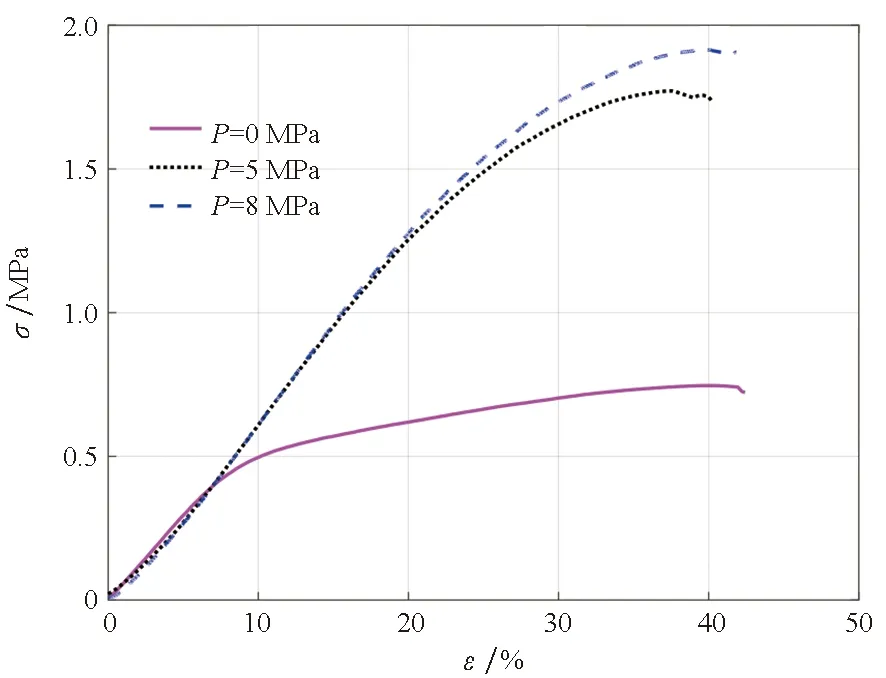
(a) V=100 mm/min

在低温和高温下，在不同的围压载荷下以1 000 mm/min的拉伸速率拉伸时推进剂的应力-应变响应曲线分别如图4和图5所示。与常压相比，在8 MPa的围压作用下，推进剂在高温下拉伸时的最大伸长率下降了约30%，而低温下的最大伸长率下降超过了70%。在低温下，推进剂的黏合剂分子链柔性降低将导致其刚度增大，而使其对高围压和高应变率更为敏感。因此，低温、高围压和高应变率的共同作用很可能会导致HTPB复合推进剂在拉伸过程中伸长率骤降。

图4 推进剂在不同围压下的应力-应变曲线(-50 ℃)Fig.4 Stress-strain curve of solid propellant under different superimposed pressure (-50 ℃)

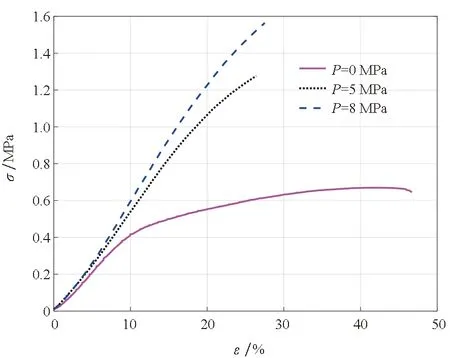
图5 推进剂在不同围压下的应力-应变曲线(70 ℃)Fig.5 Stress-strain curve of solid propellant under different superimposed pressure (70 ℃)

通过围压下某高固体含量推进剂的温度相关和应变率相关单轴拉伸试验数据，结合围压、温度和应变率的耦合效应对推进剂力学响应的影响分析，发现围压对推进剂的力学行为影响很大，在较高围压下进行推进剂单轴定速拉伸试验时，推进剂的应力-应变响应曲线上均不存在明显的“脱湿”点，且伸长率较常压下有较明显的下降趋势。当应变率较低时，围压对伸长率的影响较小，但是随着应变率的增加，在较高围压下推进剂的伸长率显著下降。伸长率最小的情况出现在高围压、高应变率和低温的共同耦合作用下，这也说明低温点火工况对于发动机而言是非常严酷的。

2 细观模型和计算结果

为了探究围压下推进剂应力-应变响应规律背后的机理，需要建立推进剂的细观模型进行进一步的分析。推进剂是一种颗粒夹杂复合材料，填充体积分数较高，颗粒的尺寸通常采用多级配，尺寸的跨度可以从几微米到数百微米。通过计算力学方法建立推进剂细观模型时需要考虑推进剂内部颗粒的级配、体积分数和粒径分布等因素，对推进剂在细观尺度下进行建模，通过商业化有限元分析软件进行模拟计算得到细观模型的应力-应变云图，借助软件的后处理直观地观察和判断推进剂的损伤和破坏情况已经成为目前的主流研究方法。

2.1 细观模型建模

为了对比围压和常压下推进剂的界面“脱湿”分离情况，分析围压下推进剂的损伤规律，建立体积分数比较高(75.6%)的颗粒夹杂模型。与试验采用的质量分数为88%(体积分数约为65.3%)的固体推进剂相比，该细观模型的体积分数较高，主要的原因是该仿真计算侧重于定性分析而非定量分析，体积分数高的推进剂损伤界面更多，更容易对比围压和常压下推进剂界面的损伤情况。此外，体积分数高的细观模型颗粒占比高，因此代表性体积单元的整体刚度也较大，在压力载荷作用下基体的大变形较小，更有利于计算结果的收敛。

AP颗粒被认为是完全弹性的，AP的弹性模量E=32 450 MPa，泊松比v=0.143 3[27]。基体采用线黏弹性材料模型，其松弛模量可采用以下的Prony级数形式表示：

(1)

Prony级数的参数由某推进剂基体的应力松弛试验数据拟合获得，本研究采用的推进剂松弛模量数据如表1所示。基体的初始模量E0=1.123 MPa，泊松比v=0.499 5。

表1 复合推进剂基体的松弛模量拟合数据

采用双线性内聚力模型来定义加载过程中颗粒和基体界面的损伤。表征界面损伤的三个参数，即初始刚度K0、临界应力T和破坏距离δf(如图6所示)。本文采用的临界应力为0.665 MPa，初始刚度为15 000 MPa/mm，破坏距离为0.368 mm[19]。

图6 双线性模型损伤参数示意图Fig.6 Schematic diagram of damage parameters for bilinear model

建立的颗粒夹杂几何模型如图7所示，计算施加的载荷和位移边界条件如图8所示。在平行于X轴和Y轴的其中一条边均施加对称约束，沿着Y轴方向施加位移载荷，在另外两个未施加对称约束位移的边界施加压强载荷，本计算中施加的围压载荷是5 MPa。

图7 体积分数为75.6%的颗粒夹杂几何模型Fig.7 Geometric model with a volume fraction of 75.6%

图8 有限元模型的载荷和边界条件Fig.8 Loads and boundary conditions for finite element model

2.2 计算结果

计算结束后，在后处理过程中通过提取从面节点与主面的距离，即可判定颗粒和基体界面的损伤情况，本文在常压和5 MPa围压加载情况下，均提取从面节点与主面距离大于0.05 μm的损伤界面，对比推进剂的界面损伤演化过程。仿真计算中采用的应变率为100%/s，选取拉伸过程中从15%到50%的四个应变值，比较常压和5 MPa围压加载情况下推进剂界面的损伤情况。

提取在常压和5 MPa围压下拉伸过程中的损伤界面(如图9～12所示)。可以看出，当以100%/s的高应变率加载时，随着应变的增大，常压下颗粒与基体的“脱湿”界面在拉伸过程中形成的空洞也在逐渐增大，损伤程度逐步加深。当应变增加到50%时，整个推进剂试样的损伤断裂带已经比较明显。与常压相比，推进剂的损伤演化进程在围压下要缓慢很多。在围压下，随着应变的增加，损伤界面的数量虽然也在持续增加，但是界面的损伤程度却没有明显的加深。并且在围压下推进剂内部损伤界面的数量较常压下显著减少，说明围压在一定程度上抑制了推进剂的“脱湿”损伤演化。

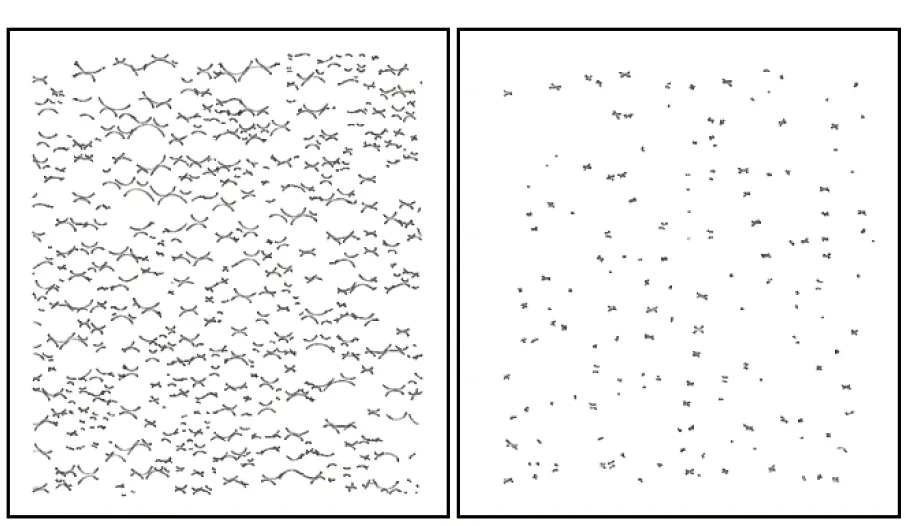
(a) 常压(a) Atmospheric (b) 5 MPa围压(b) 5 MPa superimposed pressure图9 15%应变时常压和5 MPa围压下的损伤界面对比Fig.9 Comparison of damaged interfaces at strain of 15% under atmospheric and 5 MPa superimposed pressures

(a) 常压(a) Atmospheric (b) 5 MPa围压(b) 5 MPa superimposed pressure图10 26%应变时常压和5 MPa围压下的损伤界面对比Fig.10 Comparison of damaged interfaces at strain of 26% under atmospheric and 5 MPa superimposed pressures

(a) 常压(a) Atmospheric (b) 5 MPa围压(b) 5 MPa superimposed pressure图11 39%应变时常压和5 MPa围压下的损伤界面对比Fig.11 Comparison of damaged interfaces at strain of 39% under atmospheric and 5 MPa superimposed pressures

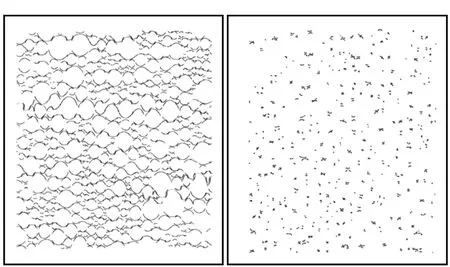
(a) 常压(a) Atmospheric (b) 5 MPa围压(b) 5 MPa superimposed pressure图12 50%应变时常压和5 MPa围压下的损伤界面对比Fig.12 Comparison of damaged interfaces at strain of 50% under atmospheric and 5 MPa superimposed pressures

3 电镜扫描和结果分析

围压会抑制推进剂的界面“脱湿”，因此在围压下推进剂拉伸的应力-应变曲线上“脱湿”拐点不明显。另外，推进剂在拉伸的过程中，由于泊松效应造成横向收缩，再加上围压载荷的作用，在颗粒界面上会产生比较大的接触应力，通过仿真计算得到的加载过程中颗粒之间的接触压力示意图如图13所示。随着拉伸位移的持续增大，围压下颗粒横向的挤压越来越严重，当颗粒的接触应力达到某个临界值之后，一部分颗粒很可能会出现破碎的情况，颗粒的破碎会导致推进剂试样整体刚度的骤降，进而出现试样突然断裂的情况。

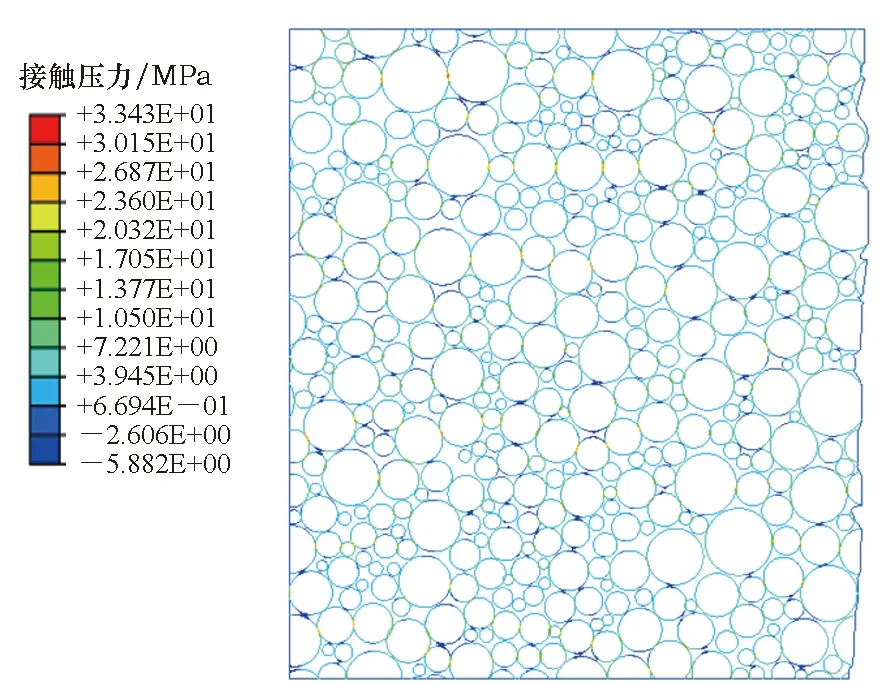
图13 颗粒之间的接触压力示意图Fig.13 Schematic diagram of contact pressure between particles

为了深入研究围压下推进剂的损伤特性，有必要对推进剂的细观损伤形貌进行分析。推进剂最严酷的工作状态是在高围压、高应变率和低温情况下的耦合，因此将通过扫描电镜(scanning electron microscope, SEM)方法观察推进剂试样在低温为-50 ℃、拉伸速率为1 000 mm/min、围压分别为0 MPa、2 MPa、5 MPa和8 MPa的断面形貌(见图14)。

(a) 0 MPa

如图14(a)所示，在常压下拉伸时，推进剂试样断面的颗粒完整，并且颗粒“脱湿”的位置可以非常清晰地看到完整的颗粒边界。在推进剂颗粒与基体的界面或基体上，在拉伸载荷作用下出现空洞并不断增大，直至颗粒和基体完全脱开或者基体被拉断。当有围压载荷作用时，从图14(b)方框所示位置可以看出推进剂试样断面出现了颗粒破碎情况。由于在拉伸过程中孔洞无法自由扩展，推进剂的“脱湿”被抑制，同时推进剂内部的颗粒在围压载荷作用下相互挤压，在颗粒边界上产生应力集中，进而导致了颗粒破碎情况的出现。但是由于围压载荷相对较小(2 MPa)，大部分颗粒仍是完整的。此外，依然可以观察到颗粒从基体位置完全脱出留下的痕迹，这意味着“脱湿”仍然是围压较低的情况下一种重要的损伤表现形式。因此，在较低的围压载荷作用下，颗粒“脱湿”和颗粒破碎是同时发生的，而这两种破坏模式会共同导致推进剂试样的最终破坏。当围压增加到5 MPa时颗粒的“脱湿”现象已经很难看到(见图14(c))，并且有更多的颗粒破碎成小的碎块。随着围压载荷继续增大到8 MPa，颗粒破碎的数量更多并且散布面积更大(见图14(d))，在整个扫描区域内几乎看不到完整的颗粒。推进剂是一种颗粒增强材料，颗粒破碎后将无法再对推进剂产生增强作用，推进剂试样将在拉伸到一定程度后突然断裂。

4 结论

本文基于自行开发的围压加载试验系统，通过开展复合固体推进剂在不同围压、温度和应变率下的单轴拉伸试验来研究围压、温度和应变率的耦合作用对推进剂力学行为的影响。同时，通过细观力学仿真和试验相结合的手段分析了围压下推进剂的破坏机理。得到以下结论：

1)围压会抑制推进剂的“脱湿”，推进剂在围压作用下进行拉伸时，应力-应变曲线没有明显的“脱湿”点。

2)推进剂的伸长率在围压下较常压下有明显的下降趋势。伸长率最小的情况出现在高围压、高应变率和低温的共同耦合作用下。

3)在常压下，推进剂的损伤形式以颗粒“脱湿”为主。当有围压载荷作用时，颗粒的破碎也变成推进剂损伤的一种重要表现形式。随着围压载荷的逐渐增加，推进剂的损伤形式从以颗粒“脱湿”为主转变成以颗粒破碎为主。