含脉冲负载的综合电力系统储能优化配置研究*

高雪平，付立军，纪 锋，张 彦，黄美娴

(海军工程大学 舰船综合电力技术国防科技重点实验室， 湖北 武汉 430033)

舰船综合电力系统(integrated power system, IPS)具有高可靠性和灵活性、低噪声能级，同时能够简化舰船动力系统结构、提高系统运行效率，代表着未来舰船动力系统的发展方向[1-3]。随着以电磁弹射系统、电磁轨道炮等为代表的舰载高能脉冲武器研究的不断发展，其上舰应用成为一种趋势，将极大地增强舰船的战斗力[4]。然而，高能脉冲武器具有瞬时大功率、周期性暂态的动态特性，会对容量有限的综合电力系统带来严重冲击，需要配备储能装置来支撑其上舰，储能装置同时兼顾提升系统电能品质及可靠性的重要作用[5-6]。

通常，考虑到舰船综合电力系统工作环境限制和高能负载的脉冲特性，适用于综合电力系统的储能类型主要包括锂电池、超级电容器和飞轮储能[7-8]。然而，上述储能装置在能量密度、功率密度、响应时间等方面差异较大，在综合电力系统中的应用仍有两个主要问题需要解决：一是如何选择最优的储能形式以满足脉冲负载需求；二是所选择的储能装置如何进行优化配置来满足舰船空间限制和机动性的要求。

目前，国外学者针对综合电力系统中储能装置的选型及优化配置有着较多的研究。在选型方面，通常可以分为单一储能装置和多种储能装置混合；在优化配置方面，则通常针对经济性、体积、CO2排放量等单目标优化和多目标优化[8-12]。文献[8]以补偿脉冲负载效果最优为目标，采用对比仿真对不同容量组合的混合储能系统进行了研究，但是未考虑储能装置质量和体积方面的限制。文献[9]对含有储能的综合电力系统进行了以经济性最优为目标的优化配置，然而未考虑脉冲负载特性及储能体积等关键问题。文献[10]给出了一种评价储能系统的位置和体积对舰船生命力和供电品质的影响的方法，并采用粒子群优化算法对该多目标最优问题进行了求解。文献[11-12]对电压波动和储能装置体积等进行了优化。然而上述的配置没有对储能装置的选择给出理论依据，并且优化配置未兼顾脉冲负载的具体特性和系统对储能的体积及质量方面的限制。

此外，在直流微网和电动汽车领域，国内外也有较多关于储能优化配置的研究。文献[13]对微网中储能类型选取、功率容量配置、平抑控制算法及能量管理策略进行了综述，并对未来研究方向进行了探讨。文献[14]提出了一种基于滤波法的微网多目标规划设计方法，考虑了蓄电池的循环寿命的优化。文献[15]对电动汽车中由蓄电池和超级电容器组成的混合储能系统进行了容量和蓄电池寿命的优化。文献[16]对超导储能和电池储能相结合的混合储能系统通过协调控制策略实现各储能装置性能的优化。文献[17]提出了储能装置在分布式系统中的最优接入点配置算法。求解此类问题的算法包括遗传算法、粒子群算法、自适应多目标差分算法、混沌自由搜索算法等[18-21]。但是上述优化配置模型中负载特性不同于船网，优化目标也非船网最迫切的需求，因此无法直接应用于综合电力系统储能容量配置。

为此，本文结合脉冲负载功率需求和舰船综合电力系统对储能的体积和质量限制，基于层次分析法和带权极小模理想点法，提出一种储能装置综合性能评价函数。在此基础上，以评价函数为优化目标，结合系统的各项约束，建立储能装置优化配置模型，并采用差分进化算法进行求解。以锂电池和超级电容器为例，通过对比得到不同储能装置的性能评价指标及最优配置方案，为舰船综合电力系统中储能装置的选择和配置提供了理论依据。

1 舰船综合电力系统模型

1.1 典型综合电力系统结构

本文研究的舰船综合电力系统拓扑结构如图1所示[22]，该系统采用中压直流环网供电，能够提升系统可靠性和运行效率。带整流系统的主发电机模块(G1、G2)协同辅助发电机模块(AG1、AG2)为全船负载供电；推进模块是由变频器驱动的推进电机(M1、M2)组成，为舰船提供动力；区域配电模块通常由功率转换模块(power conversion module, PCM)和日用负载组成；脉冲负载PL主要包括激光武器、电磁轨道炮等高能脉冲负载；储能系统(energy storage, ES)通过变流器连接到直流母线；左右舷直流母线通过艏艉断路器连接。

图1 典型舰船综合电力系统结构Fig.1 Typical diagram of vessel integrated power system

1.2 典型高能武器负载特性

舰船综合电力系统中的负载可以根据其功率特性分为常规负载和高能脉冲负载，其工作特性分别如图2(a)、(b)所示[5]。

图2 舰船综合电力系统典型负载特性Fig.2 Typical load characteristic of integrated power system

其中，常规负载具有非周期性缓变、突增突减功率小的特点。推进负载作为常规负载中的主要部分，其加减载通常根据发电机的爬坡能力来缓慢进行；而日用负载功率较小，通常通过发电系统励磁调节即可实现加减载。作为舰船战斗力核心的高能脉冲武器负载通常具有周期性重复、工作时间短、突增突减功率大的动态特性，其直接连网运行会严重影响系统的稳定性；在极端工况下，脉冲负载的突加可能使得负载总功率超过发电系统的容量，因此储能装置不可或缺。

1.3 储能装置模型

1.3.1 锂电池模型

对于锂电池型单体电路模型，采用理想电压源带内阻来表征：

Ubat0=Ubati-Ibat0Rbat0

(1)

式中，Ubat0锂电池单体的输出电压，Ubati为内电压，Rbat0和Ibat0分别为内阻和输出电流。

相应的输出功率Pbat0可以记为：

Pbat0=Ubat0Ibat0

(2)

输出功率结合放电时间可以得到相应的输出能量。此外锂电池的荷电状态(state of charge, SOC)可以记为：

(3)

式中，SOCbat0(t)为锂电池单体的实时SOC，SOCbat0(t0)为锂电池单体的初始SOC，Cbat0为锂电池单体容量。

1.3.2 锂电池寿命模型

通常，锂电池寿命被定义为容量衰减到80%时所经历的充放电循环，其主要受放电深度(depth of discharge, DOD)、环境温度和放电倍率的影响[15]。考虑舰船综合电力系统中锂电池通常需要大倍率放电来满足高能负载功率需求和舰船空间限制，因此放电倍率对寿命的影响不可忽略。由于锂电池寿命长，也即容量损失小，则考虑锂电池放电倍率影响的容量损失模型[23]为：

Qloss=Bexp[(-31 700+370.3Crate)/RT](Ah)0.55

(4)

式中：Qloss为容量损失比例；R为大气常数；T为环境温度；B为影响因子，此外，

lnB=a·e-λCrate+d

(5)

其中a=1.226，λ=0.279 7，d=9.263；Ah为安培-小时吞吐量，通常由循环次数和放电深度决定，可以记为

Ah=N·DOD·Crate

(6)

其中N为电池的循环次数，DOD为电池的放电深度；Crate为电池放电倍率。

1.3.3 超级电容模型

超级电容器单体采用理想电容带电阻模型，充电时功率Psc0和电流Isc0值为负值，放电时功率Psc0和电流Isc0为正值，超级电容端电压Usc0可以记为：

Usc0=Usci-Isc0Rsc0

(7)

式中，Rsc0为等效串联电阻，Usci为理想电容端电压。超级电容充放电功率Psc0：

Psc0=Usc0Isc0

(8)

超级电容器的输出能量为：

(9)

式中：Usc0为放电开始时超级电容器的电压；Usc(t)为放电过程结束时的电压；Cuc0为超级电容器单体的容量。进一步可以通过剩余能量得到超级电容器的SOC。

2 储能优化配置模型

2.1 储能装置性能评价函数

储能支撑脉冲负载上舰的过程中，在功率和能量方面满足高能负载需求的前提下，还有以下几个重要问题需要考虑：①十分有限的舰船空间对储能装置的体积有严格的要求；②经济性也是不可忽略的重要因素；③储能装置质量对舰船整体的机动性也有一定影响。因此，本文的研究中，着重以储能装置的体积、质量及经济性这三项综合电力系统目前最为迫切的需求参数为基础，采用带权极小模理想点来构造综合性能评价函数[24]，以对储能装置的综合性能进行评价。构造的评价函数如下：

(10)

式中：V为储能装置体积，V*为最优体积；M为储能装置质量，M*为最优质量；C为储能装置综合成本，C*为综合成本最优值；p1、p2、p3分别为各项的权重系数。可以看出，所提指标越小，储能装置综合性能越好。此外，该函数可以根据需求进一步进行扩充，具有灵活性和扩展性。

2.2 基于层次分析法的权重确定算法

层次分析法是一种主观权重决策方式，使用此方法解决问题时，评价系统将会按其属性被划分为若干子系统，然后属于各个子系统的指标会被量化和归一化处理以建立判断矩阵，最后通过一致性检验得到相应权重，其主要步骤如下[25]：

1)根据各指标之间的相对重要性建立判断矩阵，并通过求解特征值和特征向量以及一致性检验，得到相应权值；

2)采用前述步骤得到多位专家的指标权重，并组成相应的权重矩阵；

3)计算相关系数矩阵，并将偏离程度较大的权值提出，得到最终的权值矩阵D；

2.3 最优参考值的确定

以锂电池和超级电容器为例，分别进行以经济性、体积、质量为目标的单目标优化配置，并从两种储能装置各目标的最优解中选择最小值作为此项指标的最优参考值。首先，确定优化变量：针对超级电容器，优化变量为串联数目xsc、并联数目ysc以及放电深度DOD；针对锂电池，优化变量为串联数目xbat、并联数目ybat、放电倍率Crate和放电深度DOD。其中，DOD可以根据储能装置的SOC计算得到。其次，结合优化变量得到相应的优化目标：

1)体积。以储能装置体积为目标函数的表达式为：

fi1=vixiyi

(11)

其中，vi表示储能单体体积，下标i在配置的过程中分别表示锂电池和超级电容器，下文中意义同此。

2)质量。以储能装置质量为目标函数的表达式为：

fi2=mixiyi

(12)

其中，mi表示储能单体质量。

3)经济性。考虑储能装置全周期寿命内的总成本，可以得到以经济性为目标函数的表达式：

fi3=Cin+Com+Crep

(13)

其中，Cin、Com、Crep分别为储能装置的初始投资成本、运行维护成本和更新成本。当锂电池在大倍率放电的情况下，其放电倍率对寿命的影响不可忽略，因此将放电倍率纳入优化变量之中，并将寿命折成为替换成本，来更精确地考虑储能装置的经济性。

2.4 约束条件

为保证系统安全稳定的运行，应当考虑以下几个方面的约束。

1)电压约束：锂电池和超级电容器的输出电压满足变流器前端的电压范围。

2)储能装置功率约束：储能装置输出的总功率满足脉冲负载的功率需求。

3)储能装置能量约束：储能装置一次充电存储的能量能够支撑脉冲负载运行相应的次数。

4)SOC约束：锂电池和超级电容器的SOC应该在合理的范围内，过充和过放会降低储能装置使用寿命；不同储能装置的SOC变化范围也不一样，需要根据对应的储能装置的特性加以考虑。

最终得到的约束条件表达式如式(14)所示。其中，储能装置电压、功率、能量及SOC等参数均可以由前述给出的模型及优化变量计算得到。

(14)

其中：Ubat、Pbat、Ebat、SOCbat分别代表锂电池的输出电压、输出功率、存储能量以及荷电状态；Usc、Psc、Esc、SOCsc分别代表超级电容器的输出电压、输出功率、存储能量以及荷电状态；下标max和min分别表示各项参数的上下限。

2.5 求解方法

差分进化算法是一种随机的启发式搜索算法，简单易用，以其稳健性和强大的全局寻优能力已在多个领域取得成功。本文采用该算法对所提出的优化配置模型进行求解计算，其主要步骤为：

1)生成初始种群；

2)变异操作；

3)交叉操作；

4)计算目标函数值；

5)选择操作；

6)反复执行步骤2～5，直到最大的进化代数或达到迭代停止条件。

根据所建立的优化配置模型和求解算法，得到最终的算法流程如图3所示。首先，根据脉冲负载特性和系统需求分别对锂电池和超级电容器进行以体积、质量和经济性为目标的单目标优化配置，并从配置结果中选择各个目标函数的最优值作为第二步性能评价函数的最优参考值。然后，构造储能装置性能评价函数并采用层次分析法确定相应的权重。最后，以提出的储能装置性能评价函数为目标函数，分别对锂电池和超级电容器采用差分进化算法进行优化配置，得到相应的评价指标及配置方案。

图3 储能装置优化配置计算流程Fig.3 Flow chart of optimal configuration for energy storage device

3 算例分析

3.1 系统参数

根据文献[26]可以得到典型电磁发射类高能负载的功率特性，以其为基础，通过拟合得到高能负载功率需求曲线近似如图4所示。

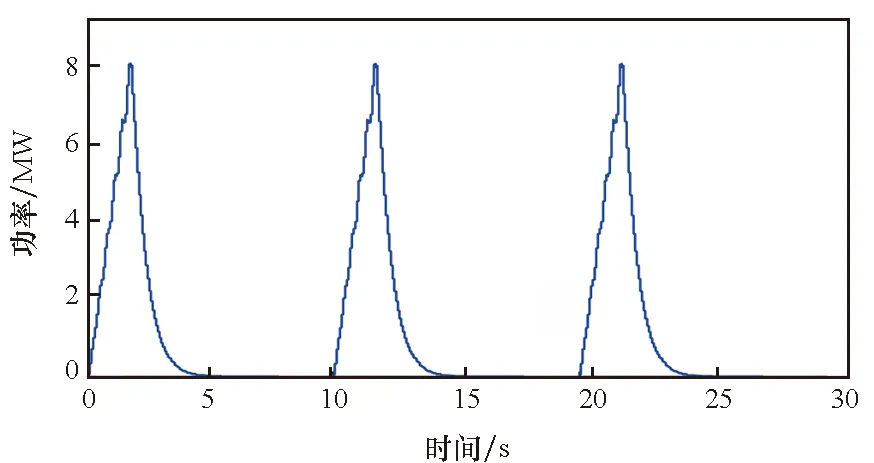
图4 典型高能负载功率需求特性Fig.4 Typical load characteristic of pulse load

其中，脉冲负载的峰值功率为8 MW，持续期间所需要的能量为16 MJ，储能装置输出电压设置为1 000 V，并通过变流器升压至4 000 V后接入直流母线，储能容量设置为支撑脉冲负载运行30次的能量。

以力神某型号锂电池和奥威某型号能量型超级电容器为例，进行储能配置计算。其中，储能装置参数如表1所示。

表1 储能装置参数

此外，在利用差分进化算法求解时，设置种群大小为500，繁衍代数为200。根据前述目标函数、约束条件及求解算法，通过在MATLAB中自编程对上述问题进行求解。

3.2 权重参数及最优参考值

3.2.1 权重系数确定

根据前述层次分析法对储能综合性能评价指标进行计算。首先根据专家意见，对前文提到的体积、质量及成本这三项指标设立矩阵，其中数值由专家打分法确立，其大小代表了指标的重要程度。其次，通过检验矩阵一致性，得到指标集{体积，质量，成本}的权重矩阵为：

根据算法，可以得到5位专家的相似度之和分别是4.616 1, 4.558 2, 4.555 5, 4.355 2, 4.661 3。其中，专家4的值最小，这意味着权重偏离程度越严重，因此剔除专家4的评价值，然后通过计算得到层次分析法确定的权重值：

{0.460，0.188，0.352}

可以看出，根据专家意见，体积在评价函数中所占的权重最大，成本次之，质量所占的权重最小。这是根据目前储能和高能负载上舰的关键制约因素是体积而得到的。

3.2.2 最优参考值确定

分别对锂电池和超级电容器采用差分进化算法对三个关键因素进行单目标优化配置，得到相应的配置结果如表2和表3所示。

表2 锂电池单目标优化配置结果

表3 超级电容器单目标优化配置结果

从锂电池的单目标优化配置结果可以看出，锂电池体积和质量最优均在放电深度和放电倍率达到约束下限时取得，而经济性最优则是在较小放电倍率和放电深度下取得。这是因为体积和质量最优要求锂电池尽可能地大倍率放电以满足相应约束，而大倍率放电会影响其寿命从而影响经济性，因此在不同放电条件下取得各自的最优解。

从超级电容器的单目标优化配置结果可以看出，超级电容器的体积、质量及经济性最优均在放电深度达到约束下限时取得。这是因为在超级电容器的配置过程中，约束因素主要是其存储的能量，当能量满足约束条件时相应的优化目标即取得最优解。

在此基础上，根据前述步骤，分别从锂电池和超级电容器的单目标优化配置结果中选取体积、质量和经济性的最小值作为最优参考值。最终可以得到储能装置性能评价函数，记为：

3.3 优化配置结果

根据所提出的储能装置性能评价函数，结合高能负载特性和相应的约束条件，采用差分进化算法，对锂电池和超级电容器进一步求解。

3.3.1 锂电池综合性能最优配置结果

针对锂电池综合性能最优的配置结果如表4所示。

表4 锂电池优化配置结果

从锂电池配置的结果可以看出，相较于体积最优在放电倍率为5 C时取得和体积及质量最优在放电倍率最大(20 C)时取得，其综合性能评价指标的最优值在适中的放电深度(23%)和放电倍率(15 C)下取得，此时指标值为0.33。

3.3.2 超级电容器综合性能最优配置结果

根据所提综合性能评价指标对超级电容器进行优化配置，结果如表5所示。

表5 超级电容器优化配置结果

对于超级电容器，其综合性能评价指标为0.48，且此时的方案同单一目标配置结果类似，其主要原因在于：超级电容器较低的能量密度是限制其各项目标函数进一步优化的主要因素，因此上述的各个优化目标的最优值均是在超级电容器存储能量满足要求的最低限度时取得，对于所提指标也是一样，因此配置结果相同。

3.3.3 结果对比

根据综合性能评价函数最小的配置方案得到锂电池和超级电容器综合性能评价的雷达图，其中各项指标越小表示性能越好，得到的对比结果如图5所示。

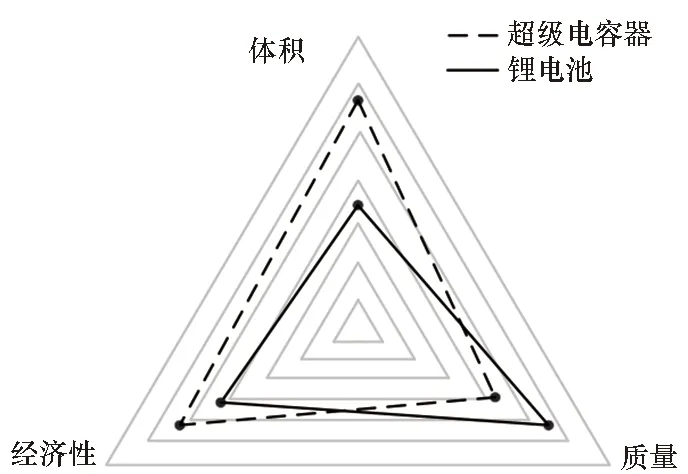
图5 不同储能各指标对比雷达图Fig.5 Radar graph of different energy storage devices

从锂电池和超级电容器配置结果的对比可以看出，锂电池的综合性能评价指标更小，即性能更优，其原因在于在综合性能评价指标的各个参考指标的取值中，锂电池在体积和经济性上均占优，并且此二者赋予的权重值也较大，而超级电容器只在质量上占优。

此外，锂电池在性能指标最优时的配置方案也即所给出的参考方案。可以看出，该方案兼顾锂电池经济性和体积以及质量，能够为综合电力系统中储能装置的配置提供一定的指导意义。

4 结论

针对含脉冲负载的综合电力系统储能装置，基于带权极小模理想点法和层次分析法，提出了一种储能装置性能评价函数，并以其为优化目标，采用差分进化算法，进行储能装置优化配置，得到以下结论：

1)考虑舰船综合电力系统实际需求和高能负载具体特性，在体积和经济性权重较大时，根据所提出的性能评价函数，锂电池较超级电容器有更好的综合性能，更适用于综合电力系统，为综合电力系统中储能装置的实际选型提供了理论指导。

2)所提出的评价函数构造方法具有较好的扩展性，可以推广到储能装置多目标优化配置之中，所得到的配置结果对储能装置在实际综合电力系统中的应用具有一定指导意义。