电磁发射高速旋转弹丸马格努斯效应*

李 开，鲁军勇，张 晓，冯军红，李湘平，杜佩佩

(海军工程大学 舰船综合电力技术国防科技重点实验室， 湖北 武汉 430033)

作为一种不同于化学能的新式发射技术，电磁发射技术发展迅速，发射对象大至飞机、导弹，小至无动力弹丸，应用广泛。电磁发射弹丸正朝着远程化、精确化和高效能的方向发展[1]。

电磁发射旋转弹丸采用轨道式电磁发射方式，弹丸采用一体化设计，尾部为电枢臂；脉冲电流从上导轨经电枢臂流向下导轨，在导轨和电枢臂上产生感应磁场，从而产生洛伦兹力推动弹丸前进，如图1所示。和传统的步枪子弹相比，电磁发射弹丸初速更高(Ma≥5)，有效射程更远，有着较大的应用潜力。出于提供枢轨接触力的需要，尾部通常开有电枢臂槽，使得弹丸不再轴对称。为使弹丸出膛后稳定飞行，电磁发射弹丸通常采用电磁或机械赋旋的方式，赋予其较高的出膛转速[2]。Tang等采用辅助导轨电磁起旋的方式，使弹丸高速(≥100 000 (°)/s)起旋[3]。在枪口初始扰动作用下，弹丸在俯仰方向产生攻角；高速旋转时由于马格努斯效应，会在偏航方向诱导产生侧向力和偏航力矩，影响弹丸的稳定性和射击精度。

图1 电磁发射弹丸原理Fig.1 Schematic of electromagnetic launch projectile

鉴于马格努斯效应对旋转弹箭气动特性特别是动稳定性影响显著，国内外开展了许多研究。Despirito等[4]对M910旋转弹丸绕流场进行了模拟，发现在亚/跨声速来流下，非定常RANS/LES方法与试验结果吻合较好。Klatt等[5]采用三维RANS仿真和风洞试验方法研究了6.37 mm直径弹丸的马格努斯效应成因，发现马格努斯力在10°～15°时达到最大值，大攻角情况下横截面气动分离位置的变化是导致马格努斯效应的主要原因。Roxan等[6]对炮弹和导弹的马格努斯效应进行了综述：对于旋转弹丸，小攻角时旋转会导致附面层的不对称，大攻角时旋转会改变分离涡的形状和位置；对于有翼弹，翼的马格努斯效应是重点。雷娟棉等[7]基于realizablek-ε湍流模型，对SOCBT高速旋转弹丸进行了数值仿真，发现弹体周向压力和切应力分布的畸变、边界层畸变、大攻角下涡的非对称畸变是马格努斯效应产生的主要原因，且船尾对弹体马格努斯力和力矩的影响很大。陈白冰等[8]采用旋转壁面法对SOCBT标准弹体模型的马格努斯效应进行了仿真分析；结果表明，大攻角时采用Spalart-Allmaras湍流模型可以较好地模拟旋转引起的附面层堆积和分离区的相互作用。吴放等[9]基于滑移网格技术，对超声速条件下ANF低旋尾翼弹箭开展了马格努斯效应研究，发现马格努斯效应随攻角增大而增加，且在40°～60°攻角范围内达到峰值；马格努斯力和力矩在较大转速下呈线性增大趋势。

上述文献对旋转弹箭气动力特性的研究更侧重于数值仿真方法，研究对象只包括高速旋转的轴对称炮弹或子弹以及低速旋转带翼火箭弹，对带有电枢臂槽的非轴对称高速旋转电磁发射弹丸的气动特性研究还未见诸文献。本文将采用理论分析和数值仿真方法对比考虑和不考虑电枢臂槽两种情况下弹丸的气动力，分析电枢臂侧向开槽对弹丸气动特性的影响。

1 物理模型

兼顾减阻和毁伤效果，旋转弹丸长细比为6 ∶1，即L=6D，弹丸尾部开有U形电枢臂槽，如图2所示。后续气动力和气动力矩方向定义与图2坐标系一致。力矩参考点为头部定点，转速沿x轴正向。对弹丸的绕流计算域进行多块结构网格划分，共分为164个区，274万网格，如图3(a)所示。为了对比分析电枢臂槽的影响，设计了去电枢臂槽的对照模型，如图3(b)所示。计算工况见表1。

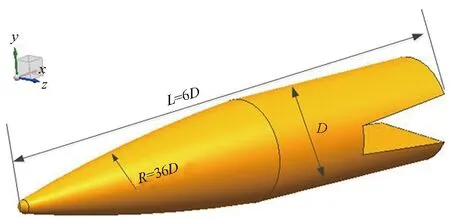
图2 旋转弹丸物理模型Fig.2 Physical model of spinning projectile

(a) 有电枢臂槽(a) With armature arm groove

2 数学模型与仿真方法验证

基于理想完全气体Navier-Stokers方程，控制方程为：

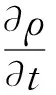
(1)

(2)

(3)

其中：ρ、p代表密度和静压；u为速度矢量；et为总温；τ、q分别代表应力张量和热流密度矢量，如式(4)、 式(5)所示。

(4)

(5)

动力黏度μ由层流黏性系数μl和湍流黏性系数μt组成，二者分别由Sutherland公式[10]和k-ωSST湍流模型确定[11]。导热系数k由分子动力学方法确定。

采用瞬态滑移网格显式求解方法[12]，初场由旋转坐标系法稳态流场计算结果确定。对流项差分采用AUSM+格式，黏性项采用二阶中心差分。显式步进时间步长由转速确定，取为旋转1°所需时间。为验证网格无关性，设计了壁面网格雷诺数y+为10、1、0.25三种网格，发现y+=1和y+=0.25时的气动力系数相差1%以内，取y+=1，与参考文献一致[13]。

图4 SOCBT几何模型Fig.4 Geometric model of SOCBT

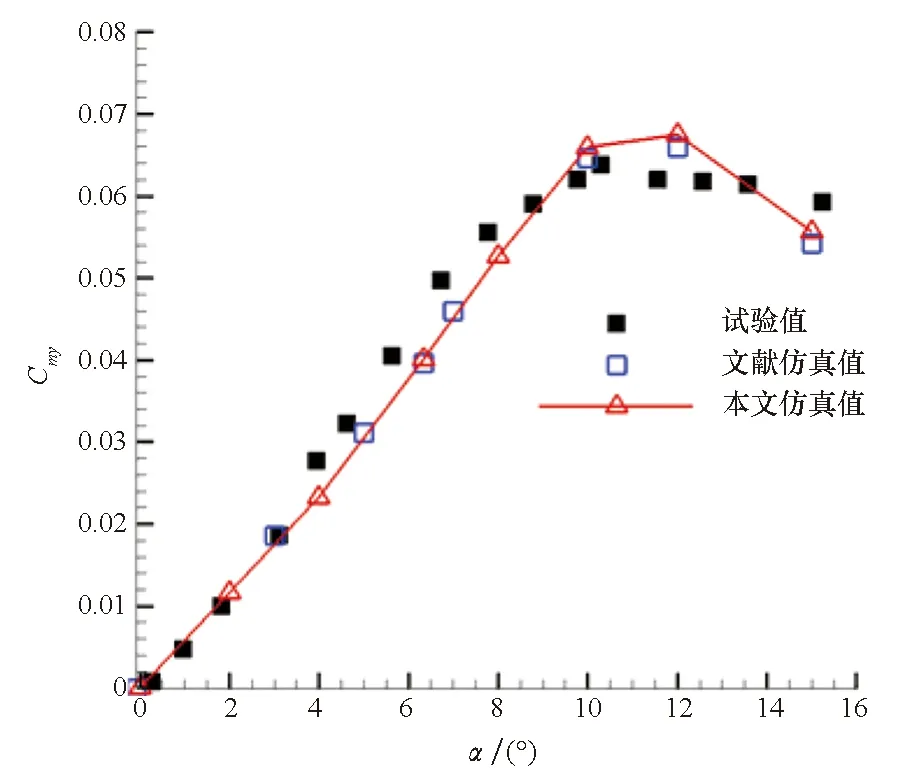
图5 SOCBT算例马格努斯力矩仿真与试验值对比Fig.5 Comparison of experimental and simulated Magnus moment for SOCBT

3 计算结果

3.1 马格努斯力和力矩

分析忽略电枢臂的轴对称模型的马格努斯效应。不同攻角和角速度下的马格努斯力矩系数如图6所示，可以看出，在0～2 000 r/s范围内，马格努斯力矩与转速成正比，且随攻角增大逐渐增大。攻角α=10°、ω=2 000 r/s对应的马格努斯力矩系数约为0.07，约为俯仰力矩的1/4，马格努斯效应较为显著。

图6 不同攻角和角速度下的马格努斯力矩系数Fig.6 Magnus moment coefficient under different attack angle and spinning speed

图7给出了无电枢臂模型在α=8°时，有无转速的横截面(x/D=5.78)流场对比。图中的黑色矢量线是流线，在正攻角下，激波位于弹体下方。可以看出，弹丸旋转后，尾部截面激波层内流场畸变，激波向-z向偏移，造成右侧(+z)壁面压力升高，左侧压力降低，从而产生绕y轴正向的马格努斯力矩。

(a) ωx=0 r/s

对于电磁发射弹丸，除了上述高速旋转引起的激波层内流场畸变带来的马格努斯力和力矩之外，电枢迎风面积的周期性变化也会对侧向力和力矩产生影响。图8给出了考虑电枢臂后的电磁发射弹丸在不同滚转角度下的尾部(x/D=5.78)横截面压力云图，图中α=8°,ωx= 2 000 r/s。可以看出，电枢臂槽内和背风面为低压区，尾部侧向力主要由下方的迎风面提供。因此，当滚转角变化时，下方迎风面的位置会出现周期性变化，从而产生诱导侧向力和力矩。在滚转角为45°和135°附近时，电枢臂迎风面积变化诱导侧向力分别达到正向和负向最大值。

(a) γ=0°

叠加两种因素后，带电枢臂槽弹丸的马格努斯力矩随滚转角周期性变化(周期为180°)，在45°和135°时分别达到最小值和最大值，如图9所示。同样原因，马格努斯力在45°和135°分别达到最大值和最小值，如图10所示。可以看出，零转速时，诱导侧向力矩仅由尾部迎风面(电枢臂)的左右不对称变化导致，一个周期内的时均马格努斯力和力矩为零；相同攻角下，随着转速的增加，激波层畸变的影响逐渐增加，马格努斯力矩曲线向正向平移，平移量近似与转速呈正比；相同转速下，随着攻角的增加，马格努斯力和力矩曲线的平移量增加，且波峰和波谷的差值越来越大，激波层内流场畸变和电枢臂迎风面积变化带来的马格努斯效应更加显著。

(a) 不同转速(α=6°)(a) Different rotational speed (α=6°)

(a) 不同转速(α=6°)(a) Different rotational speed (α=6°)

可见，不同于轴对称体，电磁发射弹丸在转动过程中，电枢臂迎风面的变化是诱导侧向力和力矩波动变化的原因。有无电枢槽马格努斯力矩的对比情况如图11所示，由图可知，峰值时刻马格努斯力矩比无电枢臂轴对称模型大50%～100%。图12给出了有无电枢臂侧向壁面压力的对比，其中有电枢工况的滚转角为135°。可以看出，转动之后，右侧(+z)和左侧(-z)的壁面压力分别位于无旋转情况的曲线上方和下方，这是正向马格努斯力矩产生的来源；电枢臂槽的存在直接导致了电枢尾部(x/D>5)壁面压力进一步降低，产生了比轴对称体更大的马格努斯力矩。

图11 有无电枢槽马格努斯力矩对比Fig.11 Comparison of Magnus moment with and without armature

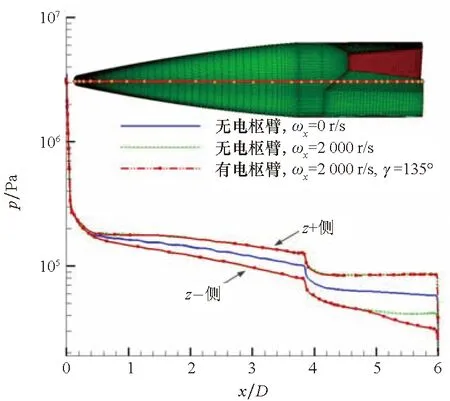
图12 有无电枢臂侧向壁面压力对比Fig.12 Comparison of lateral wall pressure with and without armature groove

3.2 纵向压心

图13给出了攻角α=8°时，不同转速下的纵向压心分布。可以看出，纵向压心位置随滚转角变化较大(绝对变化量达5%)。由于滚转角γ=0°时，弹丸尾部电枢臂槽迎风面积最大，压心系数最大，而γ=90°时最小。还可以看出，在较大滚转角范围内，随着转速的增加，压心有前移趋势，前移量约为1%。图14给出γ=90°时不同转速下壁面压力对比，可以看出，压心前移的原因是转速增加会导致背风面压力降低。压心前移将导致静稳定裕度降低，由此带来的动稳定性的变化在弹丸设计时需要特别考虑。

图13 不同转速下纵向压心分布(α=8°)Fig.13 Comparison of pressure center under different rotational speed (α=8°)

图14 不同转速下壁面压力的对比(γ=90°)Fig.14 Comparison of wall pressure under different rotational speed(γ=90°)

4 结论

以电磁发射弹丸为对象，采用滑移网格法，通过对比有无电枢臂开槽的弹丸模型的气动力特性，得到了如下结论：

1)与常规的轴对称弹丸不同，高速旋转的电磁发射弹丸的马格努斯效应更为显著，除了受激波层内流场畸变的影响，还受到电枢臂迎风面积变化的影响。后者导致马格努斯力矩随滚转角周期性变化(周期为180°)，使其在45°和135°时分别达到最小值和最大值。

2)电磁发射旋转弹丸的纵向压心位置也受到了电枢臂迎风面积变化的显著影响，绝对变化量达5%；并且随转速增加有前移的趋势：转速为2 000 r/s，压心系数绝对前移量达1%。