增量元学习IDBD算法在轴频电场信号检测中的应用*
卞 强,曾文仕,欧阳华,童余德
(海军工程大学 电气工程学院, 湖北 武汉 430033)
舰船在海水中航行时,舰船的不同金属结构在海水中会发生电化学反应,从而产生腐蚀电流。为了保护船体不被腐蚀,舰船上会人为安装外加电流阴极保护系统或牺牲阳极阴极保护系统,而阴极保护系统也会产生相应的防腐电流。腐蚀电流和防腐电流在船体结构的调制下会形成以螺旋桨转动频率为基波的时变电场,即轴频电场[1]。舰船轴频电场的频率范围一般在10 Hz以下,属于甚低频(ultra low frequency,ULF),其中包含大量有用特征信息,理论分析和实测数据均表明,该信号具有明显的线谱特征和倍频谐波成分,有效地提取其线谱成分对于水下目标识别有着十分重要的意义[2]。在实际的信号测量中,轴频电场信号的幅值通常在μV/m的量级,且随着传播距离的增大其衰减也非常快,极易被淹没在海洋环境噪声中,这就需要针对轴频微弱信号研究一种可靠有效的检测技术[3]。
近些年来,国内学者也提出了一些相应的检测手段,其中自适应线谱增强(adaptive line enhancement,ALE)技术和小波变换是目前应用相对广泛的检测方法。文献[4-5]利用小波变换具有时域局部化特性的优点,通过小波包熵等信号特征实现轴频信号的检测。但小波类算法在选择基函数和去噪阈值等方面存在困难,缺乏自适应特性。也有不少学者利用自适应线谱增强技术[6-8]来处理舰船轴频电场,但是都没有考虑算法的固定步长所带来的影响,导致算法鲁棒性较低,适用范围和应用价值大打折扣。其他应用较多的检测手段还有MUSIC算法[9-10],该算法能分辨同频信号源,但不能分辨相干信号源,容易造成错报或多报。
本文提出了一种利用IDBD(incremental delta-bar-delta)结合最小均方(least mean square, LMS)算法改进的自适应线谱增强器,通过IDBD算法的学习再学习机制,实现了自动调整学习步长参数,有效解决了固定步长带来的负面效应。实验结果表明此算法能有效地从宽带海洋环境噪声中分离出被其淹没的窄带微弱轴频电场信号,且其性能优于普通的自适应线谱增强器,极大提高了低信噪比条件下的线谱检测能力。
1 自适应噪声消除
当某个窄带周期信号被淹没在宽带背景噪声中时,这时信号和噪声的频谱混叠在一起,传统的带通滤波器便无法有效地将其分离出来,而自适应滤波器能够很好地解决这一难题。自适应滤波器利用信号的统计特性,能够在未知环境下有效地跟踪时变统计量,这是一般非自适应方法所不具备的。自适应滤波的基本原理是利用输入向量和期望响应来计算估计误差,并用该误差控制滤波器的权系数。自适应滤波器大体可分为系统辨识、自适应均衡、自适应预测和干扰消除四种应用类型,本文所应用的是干扰消除的模型,其原理如图1所示。假定信号s(n)被加性噪声u(n)所污染,以两者叠加的信号做滤波器的响应d(n)=s(n)+u(n),然后利用一个与u(n)相关的参考噪声信号做滤波器的输入u′(n),利用两者之间的相关性产生一个对u(n)非常近似的逼近即y(n),从而抵消混入信号中的噪声[11-12]。

图1 消噪原理Fig.1 Schematic diagram of denoising
2 自适应线谱增强器
自适应线谱增强器是在加性噪声中对线谱进行参数估计的自适应谱估计技术,可用来检测淹没在宽带噪声环境中的窄带信号,最早是由Widrow等在1975年提出的[13]。常规的自适应消噪是利用输入参考噪声的相关性去估计期望信号中的背景噪声,而ALE则是用延时后的期望信号作为输入信号,利用相关性直接估计出所需要的轴频信号。在实际应用中,参考噪声信号往往难以独立获得,因而ALE比常规的自适应消噪更加具备实用价值。
ALE原理如图2所示,图中z-1表示后一个时刻的信号,Δ表示延迟,通常被称为ALE的预测深度,以抽样周期为单位来衡量。输入x(n)为带噪声的原始信号,经延时后得到参考信号x(n-Δ)。参考信号经过自适应滤波器得到输出信号y(n),e(n)为x(n)与y(n)间的误差信号。每一时刻的误差信号都反馈给自适应滤波器,用以激励滤波器调整M个抽头权值。ALE通过选取合适的时延Δ,使原始信号中的宽带分量(周期性较弱的信号)去相关、窄带分量(周期性较强的信号)保持相关,叠加后最终达到滤波和增强信号的目的[14]。

图2 自适应线谱增强原理Fig.2 Schematic diagram of adaptive line enhancement
3 基于IDBD算法的自适应线谱增强
元学习算法属于机器学习领域的一种,主要研究利用过去时刻的学习经验让学习系统变得更加智能和有效。简单地说,元学习就是学习再学习。在自适应学习中,元学习和基学习所在的层面是不同的,基学习算法是在基级上调整自适应系统的参数,而元学习是在元级上调整基学习的参数[15-16]。
在线性自适应滤波中,IDBD算法被看作是一种增量元学习算法,最早由Sutton于1992年首次提出[17]。对于传统的LMS算法或递推最小二乘(recursive least square, RLS)算法来说,学习步长的选取直接影响了学习系统的最终性能,因此如何让学习步长能够随着输入信号的变化自适应调整就尤为重要了[18]。IDBD算法很好地解决了这个难题,它有效地利用了学习过程中的经验使学习算法的自适应性更好。为了使LMS算法可以自适应地调整学习步长参数,可以增加一个二级自适应来改进算法性能,设计原理如图3所示。这种新的模式通过学习中的学习来满足算法功能扩展的需求,其包括两个一起工作的单独控制机制:主控制机制由估计误差e(n)驱动,作用是和传统基于LMS算法的滤波器一样控制抽头权值的自适应调整;次控制机制也是由估计误差e(n)驱动,但其目的是通过IDBD算法自动调整主控制机制里的学习步长参数。

图3 元学习原理框图Fig.3 Schematic diagram of incremental meta-learning
由于传统的LMS在自适应信号处理中的不足,本文提出基于IDBD的自适应线谱增强基自适应去噪方法。IDBD算法是DBD(delta-bar-delta)算法的改进扩展,因为它是完全增量的且只有一个自由参数,同时它也是一种元学习算法[19]。
自适应滤波器是线性组合器构成的,即输出信号是来自阵列信号的线性组合,假设输入信号{x(n-i),d(n)}(i=0,1,…,M-1),此时有:
(1)
其中,xi(n)和ωi(n)分别表示输入信号和滤波器抽头权值,M表示滤波器抽头权值的数量。
按照LMS算法的传统形式,可以写出估计误差为:
(2)

=ωi(n)+θe(n)xi(n)
(3)
式中,标量因子1/2的引入是为了数学上处理方便,θ为固定步长。
LMS算法中的步长参数在自适应学习过程中起着至关重要的作用,这个参数的赋值应该非常谨慎。在IDBD算法中,改进之后的理想情况是:可能是不相关的输入信号,应该赋予较小的学习步长;对于更加重要的相关输入信号,则应该赋予较大的学习步长。
因此,IDBD算法中时变的学习步长参数可定义如下:
μi(n)=exp(αi(n))
(4)
其中,αi(n)是IDBD算法中两个自适应记忆参数的其中一个。式(4)中的指数关系能够提供一个简单机制来产生αi(n)中的适当的学习步长,即通过相对较慢的正积累更新来改变αi(n),并且可以保证随机梯度下降的步长μi(n)总是一个正值。
因此,IDBD算法的权值更新公式可写为:
ωi(n+1)=ωi(n)+μi(n)e(n)xi(n)
(5)
类似地,由式(3)可以写出αi(n)的更新方程:
(6)

此外,对IDBD算法的第二个可自适应记忆参数进行定义:
(7)
将式(6)代入式(5),可最终得到αi(n)的更新方程如下:
αi(n+1)=αi(n)-κe(n)xi(n)hi(n)
(8)
考虑到时间更新,根据式(3)和式(6)可以写出hi(n)的递推方程:
(9)

=-xi(n)hi(n)
(10)

μi(n+1)e(n)xi(n)
(11)
记忆参数hi所起的作用是表示抽头权值ωi改变量的衰减轨迹。
两个自适应记忆参数αi和hi的递归公式导出是IDBD算法的核心思想,αi是随着当前时刻权值ωi的变化量e(n)xi(n)和过去时刻的衰减量hi成线性变化的,如果权值是正增长的,则说明当前的输入信号相关性更大,应该适当地调整学习步长使其增大以更好地逼近期望响应;反之,则应该适当地减小学习步长,从而体现了IDBD的自适应学习能力,有效地解决了LMS算法的步长效应。
4 实验仿真
4.1 实验方法
目标信号由实验室中1 ∶100舰船缩比模型测得,其螺旋桨转速约为300 r/min,为尽可能模拟海水电导率(约为3.95 (Ω·m)-1),需往池中加入工业盐进行调制。轴频电场测量系统主要由传感器、信号调理电路和数据采集系统组成。其中电场传感器采用高灵敏度的三轴Ag/AgCl电极,分别测量舰船电场的X、Y、Z三维空间上的分量,将测得的电场数据由同轴电缆传送到测量系统并存入计算机。
4.2 实验结果
实验过程中设定采样频率为2 500 Hz,将电场传感器固定在船模正下方200 cm左右,主要选取电场X轴上的分量进行处理,测量轴频电场结果如图4所示,频谱图如图5所示。

图4 轴频电场信号Fig.4 Shaft-rate electric field signal

图5 轴频电场信号的频谱Fig.5 Frequency spectrum of shaft-rate electric field signal
从图4和图5中可以看出,输入数据的信噪比极低,数据轴频电场信号已经很难从环境噪声中分离出来。LMS自适应线谱增强器的步长因子μ=0.02,滤波器阶数N=5;同样,IDBD自适应线谱增强器的元学习率参数κ=0.02,滤波器阶数N=5。分别用这两个自适应线谱增强器对混合有环境噪声的舰船辐射噪声信号进行滤波,采用LMS算法自适应线谱增强处理后的信号频谱如图6所示,采用基于IDBD算法的自适应线谱增强处理后的信号频谱如图7所示。

图6 LMS算法处理后的信号频谱Fig.6 Signal frequency spectrum processed by LMS

图7 IDBD算法处理后的信号频谱Fig.7 Signal frequency spectrum processed by IDBD
比较图6和图7可以看出,采用基于IDBD算法的ALE处理后的信号频谱的特征较基于LMS算法的更加明显,更能够真正反映轴频电场的信号特征。由频域能量谱估算可得,滤波之前(图5)的信噪比为-22.01 dB,经过IDBD算法滤波后(图7)信噪比增加至-3.64 dB,而LMS算法处理后(图6)只能提高到-10.56 dB。信号经过处理后,很大程度地抑制了背景噪声,能够有效地将窄带轴频信号分离出来,可以看出其中轴频线谱的基频在5 Hz左右,与实际船模螺旋桨的转动频率是一致的。
采用LMS算法自适应线谱增强的自适应迭代次数如图8所示,采用基于IDBD算法的自适应迭代次数如图9所示,图中纵坐标ERMSE为均方根误差。

图8 LMS算法的自适应迭代次数Fig.8 Adaptive iterative degree of LMS

图9 IDBD算法的自适应迭代次数Fig.9 Adaptive iterative degree of IDBD
由图8和图9不难看出,在同等条件下,采用基于IDBD算法的自适应线谱增强的自适应迭代次数比采用LMS算法的迭代次数要少,前者迭代次数在50次左右就可以达到稳定,而后者则需150次左右;LMS自适应线谱增强器的输出误差要比IDBD自适应线谱增强器的输出误差大很多,说明采用基于IDBD算法的自适应线谱增强能够更快更好地收敛。
为进一步检验文中算法在不同信噪比情况下的性能,将图7中滤波之后的轴频信号认作是 “纯信号”,环境噪声则由高斯白噪声替代。然后按照指定信噪比进行幅值线性叠加,以模拟生成高、中、低三种信噪比下的混合数据,处理结果如表1所示。可以看出,本文所提算法适用于不同信噪比的情况,且在低信噪比的情况下效果相对更加显著。
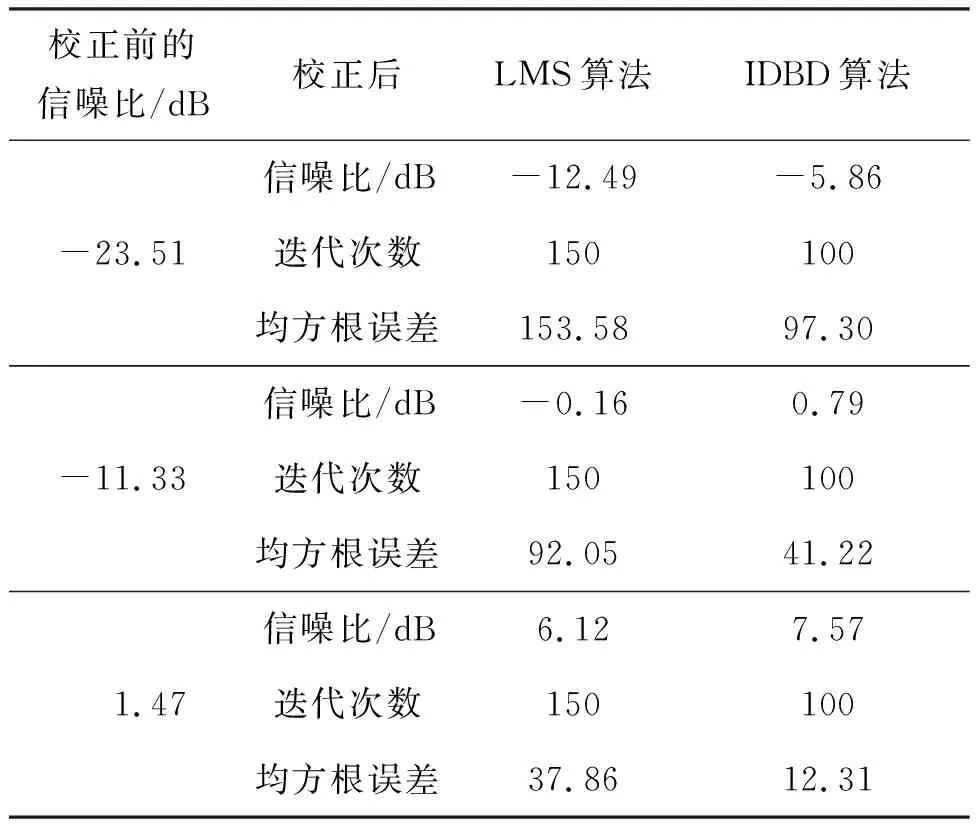
表1 不同信噪比情况下的对比
5 结论
本文提出了一种基于IDBD算法的自适应线谱增强器,基于学习再学习的思想提高了算法的信号处理能力,使其具备比传统形式算法更加优越的性能。实验结果表明基于IDBD算法的自适应线谱增强器能够有效地将微弱的轴频电场特征信号从环境背景噪声中分离出来,同时具有快速的收敛速度和较小的输出误差,为船舶轴频电场的信号检测提供了一种更加有效的技术方法。

