纳米晶硬质合金的磨削力实验与预测

詹友基， 左 振， 许永超， 王英杰， 苏乙峻

（福建工程学院 机械与汽车工程学院， 福州 350118）

硬质合金是由金属碳化物和黏结剂通过粉末冶金的方法制成的一种复合材料[1］，应用广泛.硬质合金具有硬脆难加工性，往往采用磨削加工的方法对其进行加工.磨削力是评价磨削加工的重要指标，磨削力的大小与磨削振动、磨削功率、磨削温度等密切相关[2］.同时，磨削力的变化还可反映磨粒磨损情况[3］.因此，对磨削力进行分析和预测具有重要意义.

陈永清等[4］以GCr15 钢为研究对象，探究磨削深度、砂轮线速度和工件进给速度对磨削力的影响，并建立单位宽度磨削力经验公式模型对磨削力进行预测.陈新春等[5］对WC-10Co4Cr涂层进行磨削实验，同时采用一种基于响应曲面的改进预测方法对磨削力进行预测.林佳杰等[6］针对氧化锆工程陶瓷进行磨削实验，探究进给速度、主轴转速和超声振幅等对磨削力的影响.Gopan 等[7］以高碳高铬钢为研究对象，通过设置不同工件进给速度和切削深度的参数组合，探究其磨削力的变化规律.他们将粒子群优化算法与神经网络相结合，建立了新的算法并成功预测了磨削力，为磨削力优化提供依据.罗宁[8］使用超高速平面磨削实验平台研究了磨削深度、砂轮线速度、工件进给速度对45 号钢磨削力的影响，并通过实验数据对BP 神经网络进行训练，成功预测了法向磨削力.Lipiński 等[9］用不同硬度的氧化铝砂轮进行磨削实验，研究了砂轮线速度、磨削深度、工件进给速度和砂轮硬度对磨削力的影响，并建立神经网络成功预测了磨削力，误差小于10%.赵明利等[10］对氧化铝陶瓷进行磨削加工，探究砂轮线速度、磨削深度和工件进给速度对磨削力的影响，采用改进的人工免疫系统粒子群算法对磨削力进行预测，误差小于10%，满足实际应用.田笑[11］对超细晶硬质合金GU10UF，GU15UF 和GU25UF 进行磨削实验，探究了磨削深度、工件进给速度和砂轮线速度对不同硬质合金磨削力的影响，同时使用BP神经网络对磨削力进行预测.

目前，针对纳米等级晶粒度硬质合金的磨削力研究较少.纳米晶硬质合金的晶粒度相较于普通硬质合金而言更细小，可小于0.2 μm.它的缺陷较少，物理机械性能（如硬度、韧性、耐磨性等）更强.因此，本文中以纳米晶硬质合金为研究对象，设置普通硬质合金、超细晶硬质合金为对照组，探究不同加工参数对纳米晶硬质合金磨削力的影响及不同晶粒度硬质合金间的差异，为硬质合金的磨削质量控制、刀具及模具制造选材提供参考；同时，使用RBF 神经网络对磨削力进行预测.

1 磨削力模型

在磨削加工过程中，砂轮受到径向力fr和轴向力fa的作用，相对于工件而言，砂轮会发生转动和轻微的摆动[12］.如图1 所示，将磨削力分解为3个分力，分别为切向磨削力Ft、法向磨削力Fn和轴向磨削力Fa.图中ds为砂轮直径，νs为砂轮线速度.

图1 磨削力三维分解示意图Fig.1 Three dimensional decomposition diagram of grinding force

切向磨削力方向与加工方向相同，起切除材料作用.法向磨削力方向与砂轮径向一致，其大小往往会影响材料表面质量.轴向磨削力方向与砂轮轴向一致.当砂轮质量合格且安装正确时，一般不会发生过大的偏摆，因此轴向磨削力较小，可以忽略不计.此时的磨削力可简化为由切向磨削力和法向磨削力合成且两力共面.在进行实验时，可将磨削力分解为与磨削方向垂直的磨削力Fc和与磨削方向平行的磨削力Fb，这种分解方式便于测力台的安装.磨削力的分解简图如图2 所示，其中α 为Fn与工件垂直方向的夹角[13］，ap为磨削深度.

图2 磨削力平面分解示意图Fig.2 Schematic diagram of plane decomposition of grinding force

由图2 可知，α 与ap相关，当进行小切深磨削加工时，该角度很小，此时sin α 趋近于0，cos α趋近于1.

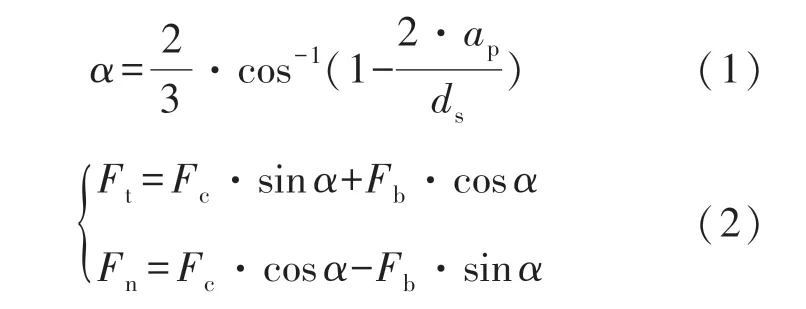
由式（1）（2）可知， Ft与Fb，Fn与Fc可近似相等.因此，可用实验测得的水平磨削力和垂直磨削力代替理论上的切向磨削力和法向磨削力，测力仪在磨削过程中所测得的磨削力即为Fb和Fc.

2 磨削硬质合金实验

磨削实验所用磨床为BLOHM ORBIT-25 精密平面磨床，使用陶瓷结合剂金刚石砂轮进行磨削，砂轮粒度代号为230／270，最高转速为50 m／s.磨削材料为纳米晶硬质合金GU092、超细晶硬质合金GU15UF 和普通硬质合金YG6X.磨削力使用Kistler 9257B 测力仪进行测量.材料性能参数如表1 所列，实验具体数值列于表2，其中νw为工件进给速度.

表1 材料参数表Table 1 Material parameters

表2 实验取值Table 2 Experimental value

3 实验结果与分析

3.1 砂轮线速度对磨削力的影响

在磨削实验中，保持工件进给速度为38 mm／s，磨削深度依次取0.005，0.010，0.015，0.020 mm.在相同的磨削深度下，纳米晶硬质合金GU092 的磨削力随砂轮线速度的变化规律如图3、图4 所示.由图可知，其切向磨削力和法向磨削力均随砂轮线速度的提升而减小.这是因为在磨削过程中，砂轮磨粒的最大未变形切屑厚度hmax与砂轮转速有关.最大未变形切屑厚度公式如下：

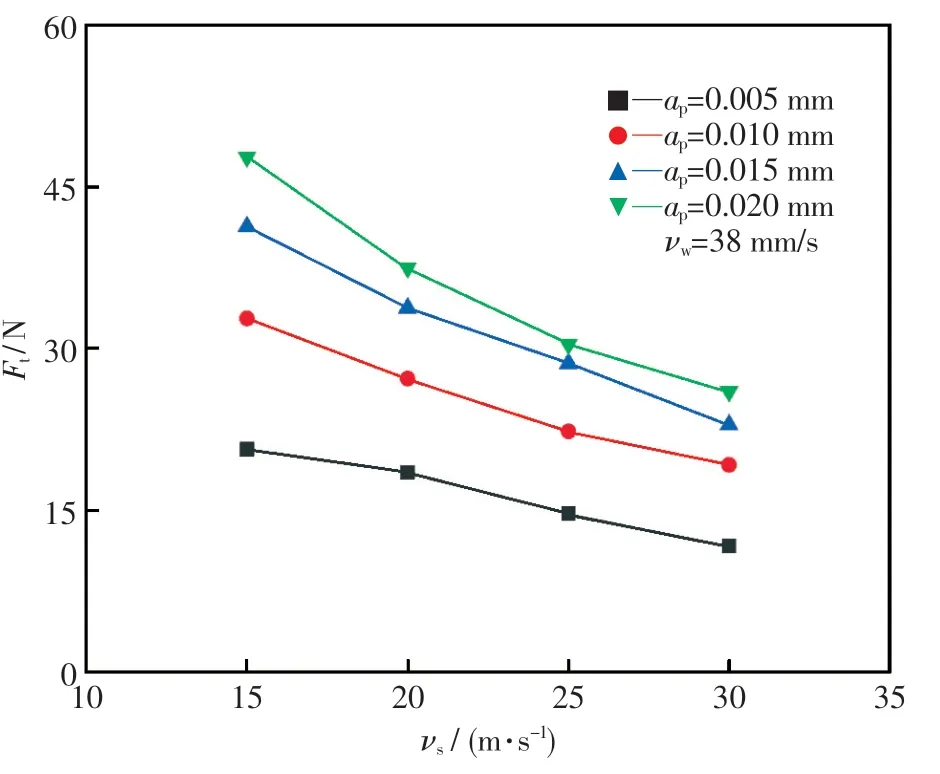
图3 vs 对Ft 的影响Fig.3 Effect of vs on Ft

图4 νs 对Fn 的影响Fig.4 Effect of νs on Fn

式中： C 为砂轮单位面积上的有效磨粒数； θ 为切屑底部夹角的1／2，通常取θ ＝60°.

由式（3）可知，砂轮线速度提升时，磨粒最大未变形切屑厚度减小[14］，此时切削厚度变小，磨削力自然减小.此外，砂轮线速度急剧增大会使材料表面出现局部高温，从而发生软化现象，这也会导致磨削力变小.

3.2 磨削深度对磨削力的影响

磨削过程中维持砂轮转速恒定（25 m／s），选取不同的工件进给速度（分别为18，28，38，48 mm／s），探究在相同工件进给速度下，磨削力随磨削深度的变化情况.由图5、图6 可知，随着磨削深度的增大，GU092 的切向磨削力和法向磨削力均增大.这是因为磨削深度的增大会变相拉长磨削弧区，使得参与磨削的砂轮有效磨粒数增加，这意味着单位时间内会有更多的材料被去除.同时，结合式（3）可知，磨削深度的增加会使磨粒的最大未变形切屑厚度增大，从而导致磨削力变大.这和陶瓷结合剂金刚石砂轮磨削超细晶硬质合金时的磨削力变化情况相似[15］.

图5 ap 对Ft 的影响Fig.5 Effect of ap on Ft

图6 ap 对Fn 的影响Fig.6 Effect of ap on Fn

3.3 工件进给速度对磨削力的影响

保持磨削深度为0.005 mm，当砂轮线速度分别为15，20，25 和30 m／s 时，磨削力随工件进给速度的变化如图7、图8 所示.由图可知，GU092 的切向磨削力和法向磨削力均随工件进给速度的增大而增大.结合式（3）可知，随着工件进给速度的增大，砂轮磨粒的最大未变形切屑厚度会增大.同时，当工件进给速度增大时，磨削区域内通过的有效磨粒数也会增加.因此，磨粒与材料之间的摩擦和冲击加剧，总的磨削力变大.

图7 νw 对Ft 的影响Fig.7 Effect of νw on Ft

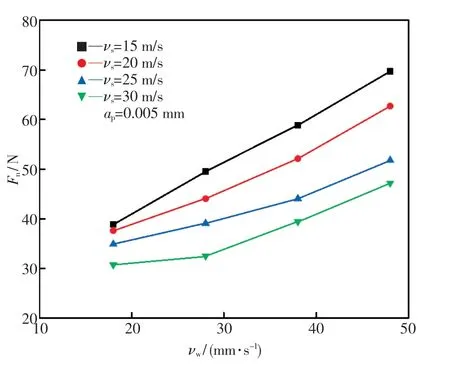
图8 νw 对Fn 的影响Fig.8 Effect of νw on Fn

3.4 不同晶粒度硬质合金间的磨削力对比

图9 显示了不同晶粒度硬质合金间的磨削力对比情况.当ap＝0.015 mm，νs＝30 m／s 时，不同晶粒度硬质合金的磨削力随工件进给速度的变化如图9（a）（b）所示；当ap＝0.01 mm，νw＝18 mm／s时，不同晶粒度硬质合金的磨削力随砂轮线速度的变化情况如图9（c）（d）所示；当νw＝28 mm／s，νs＝10 m／s时，不同晶粒度硬质合金的磨削力随磨削深度的变化如图9（e）（f）所示.由表1 可知，YG6X 晶粒度＞GU15UF 晶粒度＞GU092 晶粒度.由图9 可知，YG6X 磨削力＞GU15UF 磨削力＞GU092 磨削力.因此，随着晶粒度变小，磨削力逐渐减小.此外，材料的硬度随晶粒度的增大而减小，韧性随晶粒度的增大而逐渐增大.由磨削力大小变化情况可以看出，材料的物理机械性能也会对磨削力产生影响，这和磨削传统硬质合金时的磨削力变化规律类似[16］.

图9 不同晶粒度硬质合金之间的磨削力对比Fig.9 Comparison of grinding forces between cemented carbides with different grain sizes

3.5 磨削力的三元回归分析

对磨削力进行三元回归分析，结果如图10、图11 所示.由图可知，在模型中，磨削深度对磨削力的影响最大，其次是工件进给速度的影响，砂轮线速度的影响最小.磨削深度与进给速度呈正相关，与砂轮线速度呈负相关.当材料去除率为定值时，为了减小磨削力，可考虑采用减小磨削深度、增大工件进给速度等措施.由回归分析可知：模型的相关系数R2分别为0.940 56（针对Ft）和0.952 63（针对Fn），这表明磨削参数相关性成立；模型的F 值分别为1 567.31（针对Ft）和935.42（针对Fn），查F 分布表可知，二者的F 检定值均大于4.13，证明文中所建立的回归模型相对准确.

图10 切向磨削力回归分析Fig.10 Regression analysis of tangential grinding force

图11 法向磨削力回归分析Fig.11 Regression analysis of normal grinding force

4 RBF 神经网络的磨削力预测分析

4.1 BP 与RBF 神经网络介绍

BP 神经网络应用广泛，具有优秀的学习能力、非映射能力和容错能力.但该网络也存在着收敛效率低、学习速度慢等问题，在处理局部极小问题上仍存在不足.与BP 神经网络相比，RBF 神经网络具有全局逼近拟合的能力，可以逼近任何非线性函数且精度更高.RBF 神经网络分为输入层、隐藏层和输出层.常见的RBF 神经网络结构如图12 所示.其径向基函数一般为高斯函数，该函数具有结构简单、便于操作等优点.

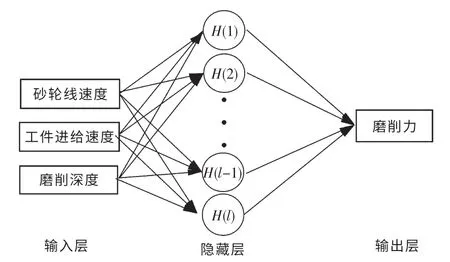
图12 RBF 网络框架图Fig.12 RBF network framework

4.2 RBF 与BP 神经网络的磨削力预测结果对比

使用MATLAB 软件完成RBF 及BP 神经网络代码的编写、训练和仿真.将纳米晶硬质合金GU092 的48 组训练样本导入MATLAB 中，对神经网络进行构建与训练，并对16 组正交实验数据进行预测，两种神经网络的磨削力预测结果对比如图13、图14 所示.由图可知，RBF 及BP 神经网络的磨削力预测值变化趋势和验证值变化趋势基本一致.图中红圈所示即为RBF 神经网络的磨削力预测值，除少部分红圈中心偏离验证值外（如切向磨削力的样本3、样本11、样本13 及法向磨削力的样本3、样本4），其他大部分红圈中心均靠近验证值.BP 神经网络的磨削力预测值大部分落在红圈外，这表明其磨削力预测值与RBF 神经网络的磨削力预测值有差距.从整体来看，RBF 神经网络的磨削力预测值更接近验证值.

图13 切向磨削力预测结果对比Fig.13 Comparison of tangential grinding forceprediction results

图14 法向磨削力预测结果对比Fig.14 Comparison of normal grinding force prediction results

4.3 RBF 与BP 神经网络的磨削力预测相对误差分析

两种神经网络的磨削力验证值、预测值和相对误差列于表3、表4.从表中可以看出：BP 神经网络的切向磨削力预测值最大相对误差为16.747%，RBF 神经网络的切向磨削力预测值最大相对误差为15.121%；两种神经网络的法向磨削力预测值最大相对误差分别为14.006%和9.689%.这种大的相对误差可能是磨削力实验数据本身的问题所致.除去最大相对误差后可以发现，其余相对误差均在10%以内. 其中RBF 和BP 神经网络的切向磨削力预测值的相对误差均值分别为3.27%和6.24%， 法向磨削力预测值的相对误差均值分别为2.50%和4.26%. 由此可见， RBF 神经网络的磨削力预测值的相对误差均值更小.

表3 切向磨削力预测结果对比Table 3 Comparison of tangential grinding force prediction results

表4 法向磨削力预测结果对比Table 4 Comparison of predicted values of normal grinding force results

4.4 RBF 与BP 神经网络的磨削力预测绝对误差分析

两种神经网络的磨削力预测值与验证值的绝对误差分别如图15、图16 所示.由图可知，与BP神经网络磨削力预测的绝对误差曲线相比，RBF神经网络磨削力预测的绝对误差曲线更为平缓.RBF 神经网络预测的切向和法向磨削力绝对误差均值分别为0.21 和0.71 N. BP 神经网络预测的切向和法向磨削力绝对误差均值分别为-0.34和0.82 N.无论是切向磨削力还是法向磨削力，RBF 神经网络预测的绝对误差均值（绝对值）都小于BP 神经网络预测的绝对误差均值（绝对值）.这表明RBF 神经网络的磨削力预测值比BP神经网络的磨削力预测值偏离验证值的程度更小，即更接近验证值.这一点从二者的切向磨削力和法向磨削力的预测结果对比图中也可以看出（见图13 和14）. 由此可见，与BP 神经网络的磨削力预测结果相比，RBF 神经网络的磨削力预测结果误差较小，准确度更高.这表明RBF 神经网络预测模型可以对磨削过程中的磨削力进行更准确的预测.

图15 切向磨削力预测绝对误差对比Fig.15 Comparison of tangential grinding force prediction absolute error

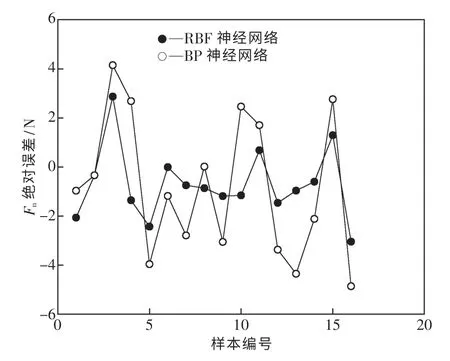
图16 法向磨削力预测绝对误差对比Fig.16 Comparison of normal grinding force prediction absolute error

5 结 论

（1）对硬质合金而言，磨削力随着砂轮线速度的增大而减小，随着工件进给速度和磨削深度的增大而增大.磨削深度对磨削力的影响最大，工件进给速度的影响次之，砂轮线速度的影响最小.

（2）磨削力随晶粒度的变小而减小，相较于普通硬质合金而言，纳米晶硬质合金的磨削力较小，物理机械性能更好.

（3）构建的RBF 神经网络模型对磨削力的预测误差较小，其切向和法向磨削力预测的相对误差均值分别为3.27%和2.50%，可以进行磨削力的准确预测.