铁矿石颗粒尺度相变传热过程的数值模拟

郭苏雅， 周 鹏， 华晴赉， 曾 嘉， 崔佳鑫， 蒋友源， 鄂殿玉，

（1. 江西理工大学 江西省颗粒系统仿真与模拟重点实验室， 江西 赣州 341000；2. 湖南华菱湘潭钢铁有限公司， 湖南 湘潭 411101）

软熔带是高炉内部非常重要的一个物理区域.在此区域向下运动的铁矿石经持续加热呈现软化熔融状态，并且发生相变直到变成液相（炉渣、铁水），而解析铁矿石颗粒的软化熔融相变复杂传输过程是调控、优化软熔带的基础和关键.

对于铁矿石颗粒在高炉内部的热化学行为研究， 有学者解析了铁矿石在软熔带加热软化过程[1］以及单颗粒铁矿石的还原过程[2-4］，但鲜有学者考虑铁矿石颗粒内部的温度分布情况.当传热过程中颗粒内部热阻大于外部热阻（Bi＞0.1）时，需要考虑颗粒内部温度梯度分布.虽然有一些学者解析了颗粒尺度一维径向传热过程、二维板坯[5］和三维板坯的瞬态热传导过程[6］，并将其作为研究颗粒填充床内颗粒传热[7］、热解[8］及气力输送[9］等的基础，但尚未涉及对铁矿石颗粒内部热传导及相变的研究，这主要是因为铁矿石颗粒从受热到熔化是一个非常复杂的传热过程.基于前人的研究结果发现，建立数学模型解析该过程是一种有效的研究手段.对此，有研究工作中[10］详细介绍了解析这类问题的数学模型，但由于其复杂性，除了一些极为简单的情况，几乎无法得到解析结果，因此数值方法[11］逐渐得到发展.目前，解析相变传热问题主要有两种模型：温度法模型[12］和焓法模型[13-14］.现有的采用这两种模型的研究大多基于一些理想的假设，如相变传热过程热物性恒定、边界条件为壁面温度恒定[15］或强制对流换热[16］等.但在实际的铁矿石相变传热过程中，铁矿石颗粒物相的改变导致其物性参数不断变化，同时反应环境与矿石颗粒存在较强的辐射换热.此外，温度法模型数值求解过程较为繁琐，并且可能引入不确定误差，同时考虑实际高炉内铁矿石热化学行为的复杂性，本文中采用焓法模型，对单颗粒铁矿石加热熔化过程进行分析，并考虑了铁矿石粒径、加热气流速度和加热气流温度对传热的影响，以期进一步探究高炉内铁矿石在软熔带的软熔滴落行为，从而指导高炉配料并优化操作，以保证高炉的稳定、高效运行.

1 模型描述与求解

1.1 模型描述

高炉内铁矿石颗粒在加热熔化的过程中与高温气流进行对流换热，同时与周围环境进行辐射换热，如图1 所示.本文中建立高炉内铁矿石颗粒的相变换热数学模型，并做出如下假设：①将矿石颗粒看作粒径均匀的球形颗粒；②铁矿石颗粒内部初始温度均匀；③颗粒温度只沿径向变化；④相变过程中固相、液相区中心始终重合.在本文中，气固两相传输系统中的气流处于湍流流动状态（27 000≤Re≤240 000），因此，铁矿石颗粒的传热可简化为一维非稳态传热过程，又因球形颗粒具有对称性，所以只求解径向温度分布.

图1 铁矿石颗粒加热熔化模型Fig.1 Iron ore particle heating and melting process model

根据上述假设，单颗粒铁矿石加热熔化过程中各相区域的控制方程描述如下：液相区控制方程：

固相区控制方程：

相界面控制方程：

利用焓法求解的基本思想是将焓和温度耦合在一起作为待定函数，确定焓分布，进而解析温度分布和相变界面的位置.

利用焓和温度之间的关系方程式，方程（1）～（3）可以描述为

其中，铁矿石颗粒的焓随温度变化，关系式[17］为

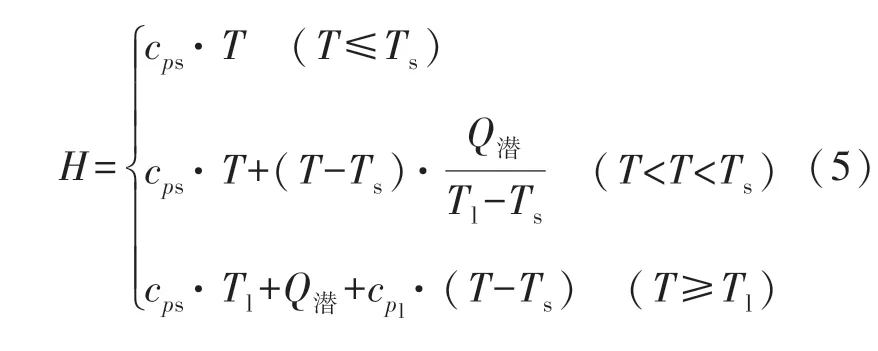
式（1）～（5）中： T 为铁矿石颗粒的温度， Ts和Tl分别为固相温度和液相温度； cps和cpl分别为固态和液态铁矿石颗粒的比定压热容； λ 是铁矿石颗粒的热导率； Q潜是铁矿石颗粒的潜热； H 是铁矿石颗粒的焓值； r 是颗粒内部的相对位置； R是铁矿石颗粒的半径；是加热时间； L 是液相界面移动距离.具体物性参数值如表1 所列.

表1 物性参数Table 1 Physical property parameter

在单个铁矿石的软化熔融过程中，考虑了对流和辐射传热，建立初始和边界条件如下：

初始条件：

边界条件：

式中： ε 为铁矿石颗粒的辐射系数； h 是铁矿石加热过程中的对流换热系数[18-19］，其中Pr 为普朗特数，表示加热气流温度下的气流黏度与平均壁面温度下的气流黏度之比.

1.2 模型求解

在完成数学建模后，采用内节点法对铁矿石颗粒加热熔化模型控制方程进行离散，离散节点分布如图2 所示.沿颗粒半径方向进行网格划分，共划分了（N＋1）个节点，其中0，1，（N-1），N 为需要特殊处理的4 个边界节点.图中表示某一时刻铁矿石颗粒熔化的情况，颗粒内部存在两个移动的相界面（固相面和液相面），两个相界面中间的区域是固液共存区域.基于以上节点划分，对模型控制方程及初始、边界条件的偏微分方程采用有限差分方法进行离散，空间和时间均采用向前差分格式，表达式为

图2 离散节点分布图Fig.2 Discrete nodes distribution

1.3 模型验证

为验证文中建立的模型的准确性，在完成了数值求解的网格无关性验证的基础上，对粒径为2 mm、流体与颗粒之间相对速度为1 m／s 的单个高温熔融炉渣颗粒相变冷却过程进行求解.图3为模型预测结果与Wang 等[20］研究结果的对比图.验证结果表明，本文中建立的描述颗粒内部相变传热的模型和求解正确可靠.

图3 模型验证Fig.3 Model validation

2 结果与分析

2.1 铁矿石相变换热特性分析

对初始温度为400 K、粒径为40 mm 的铁矿石颗粒在加热气流速度为30 m／s、温度为1 873 K工况下的相变换热过程进行了计算.铁矿石颗粒内部温度分布随时间变化如图4 所示.从图中可以看出：铁矿石颗粒在加热时外表面（r ＝R）温度先快速上升，约43 s 时达到相变起始温度（1 500 K）并开始发生熔化，且由于相变潜热的累积，外表面温度在相变起始温度处上升速度变缓；而此时在r ＝0.5R 处温度约为850 K，颗粒的中心（r＝0）温度约为750 K，形成了较大的温差，颗粒外表面的热量主要沿径向传递.随着加热过程的进行，熔化相界面逐渐向颗粒内部推移，颗粒表面升温速度减缓、中心升温速度几乎保持不变，颗粒内部的温差逐渐减小，这使得颗粒整体升温速度变缓.铁矿石颗粒中心温度在200 s 时达到相变结束温度（1 600 K），此时颗粒完全熔化.

图4 铁矿石颗粒径向温度分布Fig.4 Radial temperature distribution of an iron ore particle

铁矿石加热过程中沿径向的加热速度随时间的变化如图5 所示.从图中可以看出，颗粒在加热过程中表面和内部呈现不同的加热速度.在颗粒表面（r＝R），初始时刻加热速度可达175.69 K／s，随后加热速度逐渐降低；在r ＝0.5R 处，加热速度先逐渐增大到17.87 K／s，然后缓慢减小到1.33 K／s，随后保持着较为平缓的趋势.颗粒中心点（r＝0）加热速度稍慢，但也是先增大，后减小，再保持平缓趋势.颗粒内部出现此传热现象的原因是在加热过程开始时，颗粒外表面与外界加热气流存在较大温差，换热能力增强，温度上升速度增大；但随着加热过程的进行，二者温差逐渐缩小，从而导致温度上升速度减小.

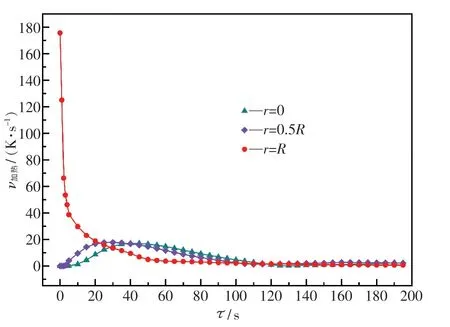
图5 铁矿石颗粒径向传热速度Fig.5 Radial heat transfer velocity of an iron ore particle

铁矿石加热过程中液相界面（液相径向厚度）随时间的推移过程如图6 所示.结合图4 可知：＝65 s 时铁矿石颗粒的外表面温度达到1 600 K，之后颗粒开始熔化，随着气流的持续加热，颗粒内部温度升高，液相界面开始向内部推移；由于颗粒内部温度梯度变大，液相界面向内移动速度越来越快，直到＝200 s 时铁矿石颗粒中心温度达到熔化温度，液相界面移动到颗粒中心，铁矿石完全熔化.

图6 铁矿石颗粒内部液相界面的移动过程Fig.6 Movement of liquid phase interface in an iron ore particle

2.2 铁矿石熔化过程中液相析出

在铁矿石熔化过程中，铁矿石颗粒要经历从固态到液态的相变过程，其中颗粒熔化的液相体积分数是相变换热过程的重要参数.图7 显示了不同影响因素下颗粒液相体积分数随时间的变化.在不同粒径大小的工况下，粒径越小，铁矿石颗粒的液相体积分数增长得越快，达到完全熔化的时间就越短.粒径为30 mm 的颗粒完全熔化的时间约为120 s，粒径为40 mm 的颗粒完全熔化时间约为200 s，即颗粒粒径增大1.3 倍，熔化时间增长1.7 倍.在不同加热气流温度的工况下，随着加热气流温度的升高，液相的体积分数随时间变化得更快，这是因为加热气流和铁矿石颗粒温差增大，以及加热速度变快会缩短颗粒熔化时间.此外，随着加热气流速度的增大，对流换热系数增大，液相界面的推移速度随时间的增加而变快，颗粒熔化时间缩短，不过缩短得并不明显.

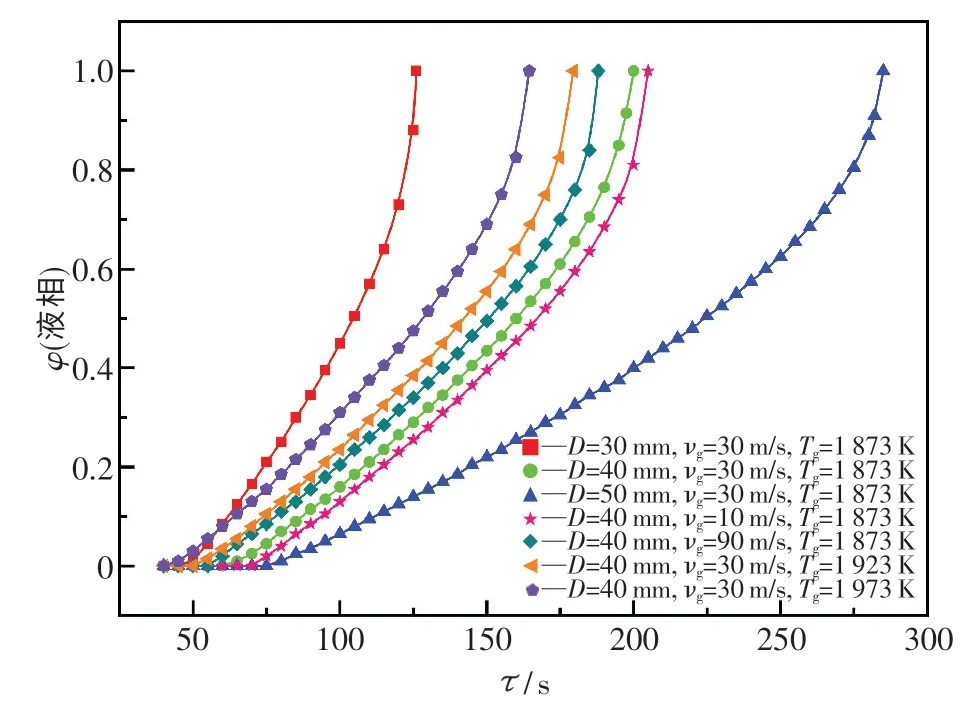
图7 铁矿石颗粒内部液相的体积分数在不同工况下的动态演变Fig.7 The evolution of liquid phase volume fraction in an iron ore particle under varied operating conditions

2.3 相变区厚度变化

铁矿石颗粒在一定温度范围内发生相变时，颗粒内部存在固相-固液共存区界面和固液共存区-液相界面，固液共存区也称相变区.相变温度范围的存在对颗粒内部的温度分布、界面运动和加热速度有显著影响，因此，建立考虑相变温度范围的模型能较为准确地预测铁矿石颗粒加热熔化过程.

图8 显示了在不同工况下铁矿石颗粒相变区厚度随时间的变化.由图可知，相界面厚度一开始为0（颗粒没有开始熔化），随着时间的增加，相变区厚度增大，直到铁矿石颗粒中心温度达到熔点1 500 K 时，相界面厚度达到最大.之后，相界面厚度逐渐减小，直到变成0 时颗粒熔化完成.对于粒径大小的影响，粒径越大，相变区的变化越缓慢，颗粒熔化时间越长.对于加热气流温度高低的影响，加热气流温度越高，颗粒熔化时间越短：加热气流温度为1 973 K 时颗粒开始熔化的时间是35 s，而加热气流温度为1 873 K 时颗粒进入相变区的时间是55 s.对于加热气流速度大小的影响，当加热气流速度为10，30，90 m／s 时，颗粒熔化时间分别为205，200，188 s，即加热气流速度从10 m／s增至30 m／s，颗粒熔化时间加快了2.4 %，加热气流速度增至90 m／s 时颗粒熔化时间加快了8.3 %.颗粒熔化时间随加热气流速度变化不明显，这是由于颗粒除了与周围气流进行对流换热外，还与周围环境进行辐射换热，尤其在高温环境中辐射换热影响增强，使得铁矿石颗粒的相变换热受周围环境的辐射换热影响较大.实际操作中增大加热气流速度，铁矿石颗粒熔化时间不会等比例缩短，且会产生更大的能耗.

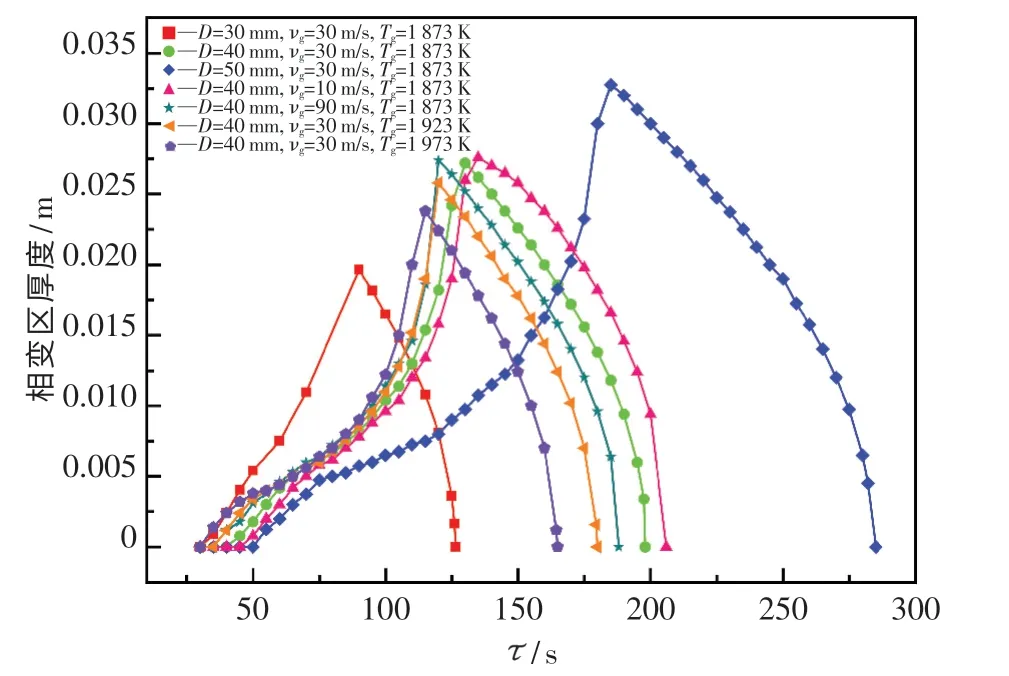
图8 铁矿石颗粒内部相变区厚度在不同工况下的动态演变Fig.8 The evolution of phase change zone thickness in an iron ore particle under different working conditions

2.4 颗粒中心与外表面温差动态演变

图9 显示了不同工况下铁矿石颗粒中心与外表面温差在相变换热过程中的动态演变.由图可知，颗粒中心与外表面温差先升高，达到最大值后逐渐减小，在经历一个相对稳定的时期后平缓下降.颗粒外表面温度升高时，由于颗粒内部热阻的存在，颗粒中心（r＝0）还没有升温，持续加热会出现最大温差；但随着时间的增加，颗粒中心温度升高，温差逐渐缩小.对于粒径大小的影响，初始加热升温时不同粒径的颗粒中心与外表面温差增长速度较为接近，直到20 s 左右，粒径为30 mm 的颗粒外表面温度开始迅速上升，使得颗粒中心与外表面温差升高到约700 K；随着时间的增加，粒径为40 mm 的颗粒外表面温度缓慢上升，直到颗粒中心与外表面温差达到800 K 左右.由图可知，粒径越大，相同时刻颗粒中心与外表面温差越大，且温差减小的时间变长.这是因为随着颗粒粒径的增大，对流换热系数减小，换热能力减弱，同时颗粒吸收更多的显热和潜热，熔化时间会大幅增加.对于不同加热气流速度和温度的影响，颗粒中心与外表面温差的变化并不明显.

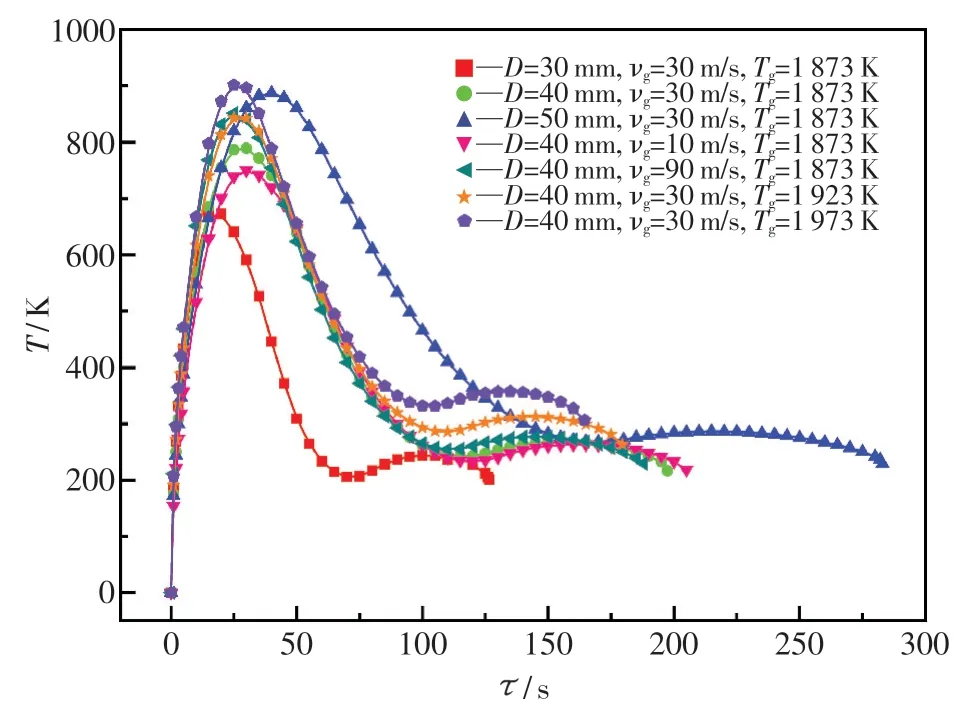
图9 铁矿石颗粒中心与外表面温差在不同工况下的动态演变Fig.9 The evolution of temperature difference between its center and out surface of an iron ore particle under varied operating conditions

3 结论

（1）铁矿石颗粒粒径大小对熔化过程的液相析出、相变区厚度和颗粒中心与外表面温差等主要参数影响最为显著.随着颗粒粒径的增大，颗粒所含的显热和潜热增大，同时颗粒外表面对流换热系数减小，换热能力减弱，颗粒内部热阻增大，导致相界面移动速度较慢，熔化时间变长.

（2）加热气流温度越高、速度越大，相界面移动速度越快，颗粒受热熔化时间越短.加热气流速度影响作用微弱，在本研究中的工况下流速增大3 倍，颗粒熔化时间缩短2.4%；流速增大9 倍，颗粒熔化时间缩短8.3%.但颗粒熔化时间随加热气流温度的升高有较大程度的缩短，主要是由于颗粒同时与周围气流进行对流换热和辐射换热，尤其是在高温环境中辐射换热影响增强，使得铁矿石颗粒的相变换热受周围环境的辐射换热影响较大.