基于相关性选择的微型计算光谱探测技术

杨 港，郭迎辉,3，蒲明博,3，李 雄，罗先刚*

1 中国科学院光电技术研究所微细加工光学技术国家重点实验室，四川 成都 610209；2 中国科学院大学光电学院，北京 100049；3 中国科学院光电技术研究所矢量光场研究中心，四川 成都 610209

1 引 言

光谱成像探测技术，是一门通过获取目标的空间信息和光谱信息，以实现目标探测和识别的技术。因具有精准、非接触检测等多项优点，光谱成像技术已广泛应用于遥感[1-3]、医学诊断[4-5]、食品安全检测[6]、环境监测[7]等领域。然而，传统的光谱成像技术通常存在采样时间长、能量效率低、难以同时获得高光谱和空间分辨率等问题。针对这些问题，来自杜克大学Bardy 团队的研究人员提出了一种利用编码孔径及色散结构对空间及光谱信息进行先编码再重建的计算型快照式光谱成像技术[8-11]，该技术可以在快照模式下同时捕获目标的空间和光谱信息，并以较少的滤波通道获取更多的光谱波段。然而，传统的计算型快照式光谱成像系统仍存在结构复杂、体积庞大等问题。

超构表面是一种可对电磁波光谱、振幅和相位进行灵活调控的人工结构功能材料，因具有结构紧凑、对电磁波灵活调控等多项优点[12-14]，超构表面已被广泛应用于三维全息[15-17]、光谱检测[18-20]、超构透镜[21-26]、超分辨率成像[27-29]等领域。为解决传统光谱成像系统存在的结构复杂、难以小型化的问题，来自清华大学Cui 团队、威斯康辛大学Yu 团队及其它团队的研究人员已提出了一些基于超构表面的计算型快照式光谱成像系统[30-37]，这些系统通常利用超构表面的宽带光谱特性，并结合压缩感知算法实现轻量化的计算型光谱成像探测。然而，现有工作中超构表面微纳结构设计，通常采用先设计大量超构表面再随机进行选择的方法，这种方法缺乏对超构表面透射谱相关性均值与重建质量的定量分析，无法保证重建质量最优。

针对上述问题，来自滨州学院的Li 等人已提出一种利用极大线性无关准则对传统宽带滤光片进行选择设计的方法[38-41]。不同于上述方法，本文定量分析了超构表面透射光谱相关性均值与重建保真度的关系，提出了一种用于微型光谱探测的超构表面设计方法。为验证所提出方法的优势，本文从众多光谱选择了10 条宽带光谱及图像光谱进行展示。相较于随机选择设计方法，本文所提出方法能对选定10 条宽带光谱及图像光谱信号的重建质量进行优化，宽带光谱重建保真度的增幅可达 13.17%，图像光谱信号的重建保真度也得到了一定的提升。此外，本文还仿真验证了基于超构表面的微型光谱探测系统的光谱特性，该系统对宽带、窄带光谱和图像光谱信号都具有较好的重建效果，具有结构紧凑、体积小的优势。

2 工作原理

本文对一种用于可见光谱范围(400 nm～700 nm)的微型光谱探测系统进行了分析。图1(a)描述了该系统的工作原理：在不同像素点上具备不同光谱信息的图像光谱信号，经透镜组后被CMOS 传感器上的多个微型光谱仪所调制，将调制信号经过压缩感知算法进行恢复处理，可获得重建图像光谱信号。图像信号中某一特定像素点所携带的光谱信号，经过置于CMOS 图像传感器上的单个微型光谱仪被调制，而重建光谱信号可由调制信号与压缩感知算法重建获得。其中置于CMOS 图像传感器上的多个微型光谱仪的示意图如图1(b)所示，而单个微型光谱仪由M=36个超构表面组成，超构表面在特定的结构参数下有着特定的透射光谱，相应的示意图如图1(c)所示。

图1 微型光谱探测。(a) 原理示意图；(b) 多个微型光谱仪的示意图；(c) 单个微型光谱仪及超构表面透射光谱的示意图Fig.1 Miniature spectral detection.(a) Schematic diagram of the working principle;(b) Schematic diagram of numerous micro-spectrometers;(c) Schematic diagram of a single micro-spectrometer and transmission spectrum of a metasurface

对于单个像素点上的光谱信号，当原始光谱入射到具有不同透射光谱的超构表面上时，第i个超构表面下方的光电探测器接收到的调制信号Yi为

其中：f(λ)为 原始入射光谱，ti(λ)为第i个超构表面的透射光谱，η (λ)为光电探测器的响应光谱，λ=λ1,λ2,λ3,······,λN为波长采样点。为简化公式，将光电探测器的响应光谱与超构表面的透射光谱进行整合，Ti(λ)=ti(λ)η(λ)，最 终 式 (1)变 换 为Yi(λ)=f(λ)Ti(λ)。当超构表面的结构数量为M时，M个超构表面下的光电探测器可以一次性接收到M个不同的信号YM，相应地式(1)变换为Y1×M=f1×NTN×M，而原始光谱f(λ) 可以通过求解上述方程来重建。

原始光谱信号f(λ)需具备稀疏性才能被高光谱探测压缩感知采集，而自然界中的大多数光谱f(λ)并不具备稀疏性，因此，需要将光谱信号映射到其他稀疏域以获得稀疏表示，使得f=Psi×x，其中Psi为稀疏变换矩阵，x为稀疏向量，则式(1)可转化为Y=T×f=T×Psi×x[42]。重建过程的原理可以用以下公式进行表示[43-45]：

其中：范数l1定义为，残差δ为极小的正常数。当残差接近0 时，可以通过预先得到稀疏解x，求解得到重建光谱f(λ)。作为压缩感知算法的其中一类，本文采用了基于贪婪算法的正交匹配追踪算法进行光谱重构，该算法能在每次迭代中，保证残差与已选传感矩阵的基正交，减少算法的迭代次数，从而保证较高的实时性。该算法对单一光谱的重建计算耗时约为2 s。

3 超构表面的数值仿真

在压缩感知算法中，由超构表面透射光谱和光电探测器响应光谱组成的Ti(λ)被称为测量矩阵，而测量矩阵是实现光谱压缩、重建还原的重要工具，因此超构表面的合理设计至关重要。本文采用有限时域差分法(FDTD)仿真了具有不同内孔图案及结构参数的超构表面，超构表面的单元结构从上到下由190 nm厚的晶体硅膜和蓝宝石衬底组成，190 nm 厚的晶体硅膜具有不同周期p和内孔图案，单元结构示意图如图2(a)所示。为满足超构表面在光谱重建中丰富透射光谱的需求，本文将结构周期p、内孔图案、孔结构参数l、w、d和旋向角θ作为其自由度，超构表面的外部周期(p)的变化范围为350 nm～750 nm，内部周期(l,w,d)的变化范围为150 nm～550 nm，占空比(l/p,w/p,d/p)的变化范围为15%～65%，旋向角θ为0°或45°，根据以上结构参数的变换范围，本文仿真出约4200 组的超构表面。

不同超构表面具有不同的内孔图案和结构参数，用橙色方框标注的超构表面的内孔图案与结构参数为十字形，p=450 nm，l=330 nm，w=140 nm，θ=0°；用黑色方框标注的超构表面的内孔图案与结构参数为十字形，p=550 nm，l=395 nm，w=215 nm，θ=45°；用蓝色方框标注的超构表面的内孔图案与结构参数为圆形，p=560 nm，d=195 nm，如图2(b)及图2(c)顶部所示。图2(c)为依据不同相关性均值对超构表面进行选择设计的示意图，图片顶部为依据相关性均值间隔[0.1～0.3]进行选择，图片底部为依据相关性均值间隔[0～1]进行选择。其中第i、j个超构表面透射光谱的相关性均值被定义为

图2 超构表面的设计。(a) 超构表面的单元结构；(b) 单个微型光谱仪的示意图；(c) 根据不同相关性均值间隔对超构表面进行选择的示意图；(d) 不同图样的超构表面透射光谱Fig.2 Design of the metasurfaces.(a) The unit cell of the metasurfaces;(b) Schematic diagram of a single micro-spectrometer;(c) Schematic diagram of the selection of metasurfaces according to different average correlation value intervals;(d) Transmission spectra of different patterns of the metasurfaces

同时，为量化分析重建光谱与原始光谱的吻合程度，本文采用重建保真度F来定义，其公式为

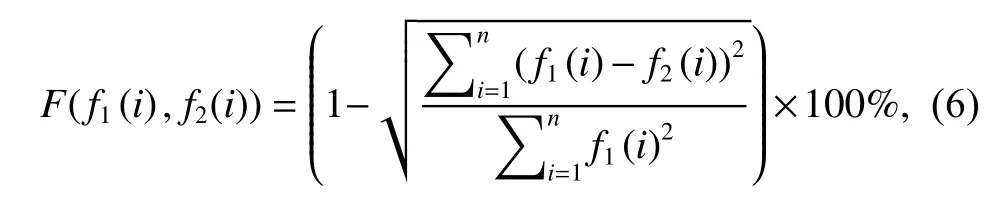
其中：f1为 原始光谱，f2为重建光谱。不同内孔图案和结构参数的超构表面具备不同的透射光谱，满足了超构表面丰富透射光谱的设计需求，在图2(b)中用不同颜色方框标注的结构所对应的透射光谱如图2(d)所示。

4 相关性均值与重建保真度分析

测量矩阵Ti(λ)由超构表面透射光谱导入，因此对超构表面的设计方法，本质是一种对测量矩阵构建优化的方法。为完成对测量矩阵的构建优化，本文定量分析了超构表面透射光谱相关性均值与重建保真度的关系，并提出一种用于微型光谱探测的超构表面设计方法。该方法的流程图如图3 左侧所示，该方法包含以下几个步骤：首先，给出一条具有特定带宽和中心波长的原始入射光谱；随后，给出多组超构表面结构透射光谱；接下来，在本文所提出的方法中，采用式(3)得到两种超构表面透射光谱的相关性值，并采用式(4)，式(5)得到M(M=36、49 或64)组超构表面的相关性均值；然后，依据不同相关性均值间隔[0.1～0.3]、[0.3～0.5]、[0.5～0.7]和[0.7～0.9]选择出M组超构表面的透射光谱；接下来，采用压缩感知算法重建原始入射光谱，

图3 本文所提出方法与传统方法的流程图Fig.3 Flow chart of our proposed methodology and traditional methodology

并通过式(6)计算原始光谱与重建光谱之间的重建保真度F；最后，当所有原始入射光谱计算完成后，可以得到不同原始入射光谱下的重建保真度F，以及超构表面透射谱相关性均值与重建保真度F的量化关系。相比之下，传统结构设计方法通常采用随机方式进行选择，图3 右侧为传统方法的流程图。本文完成了超构表面透射光谱相关性均值所有范围0～1 的计算，但计算所得的相关性均值处于0.1～0.9 区间内，没有处于相关性均值0～0.1 的区间，为保证计算及分析的准确性，本文舍弃掉了0～0.1 这段。

本文从众多光谱选择了10 条宽带光谱用于验证所提出方法的优势，采用上述两种选择设计方法对10 条选定的原始入射光谱进行重建，可得到如表1所示的重建保真度数据。如表1 数据所示，相关性均值间隔[0.1～0.3]内的超构表面所产生的光谱重建保真度均高于随机选择的超构表面所产生的光谱重建保真度，对于10 条选定的原始光谱，光谱重建保真度的增幅可达13.17%，对于其他未知原始光谱，本文所提出方法可能存在更高的重建保真度增幅。这些结果表明，相较于传统随机选择方法，本文所提出方法能在一定程度上优化光谱重建质量。此外，相关性均值间隔[0.1～0.3]的超构表面所得到的光谱重建保真度，通常优于相关性均值间隔[0.3～0.5]、[0.5～0.7]、[0.7～0.9]的超构表面所得到的重建保真度。因此在微型光谱探测技术中，低相关性均值的超构表面结构能带来更高的光谱重建保真度。

图4 展示了表1 中不同超构表面选择设计方法所产生的重建保真度。图4(a)和4(b)为汇总了表1 中的原始入射光谱1～5 及光谱6～10 的示意图。图4(c)和4(d)重点描述了在入射光谱5、光谱10 下，不同超构表面选择设计方法产生的重建保真度。如图4(c)和4(d)所示，相较于传统随机选择方法，选择相关性均值间隔[0.1～0.3]内的超构表面所产生的重建保真度均有不同程度的增幅，这表明本文所提出方法能在一定程度上提高压缩感知算法的光谱重建保真度。

如表1 数据与图4 的原始入射光谱所示，不同的原始入射光谱有着不同的光谱重建保真度及增幅，经分析后发现，当原始光谱在较短波长范围内(400 nm～450 nm)有光谱分量时，保真度增幅较低，如光谱1、2、9；当原始光谱在较短波长范围内不包含有光谱分量时，保真度增幅较高，如光谱4、5、8、10。以上结果表明，本方法保真度提升量和原始光谱相关，该方法最适用于在较短波长无光谱分量的原始光谱。

图4 表1 中不同超构表面选择设计方法所产生的重建保真度。(a)表1 中的光谱1～5；(b)表1 中的光谱6～10；(c) 在光谱5 下，采用不同的超构表面设计方法所产生的重建保真度；(d) 在光谱10 下，采用不同的超构表面设计方法所产生的重建保真度Fig.4 The reconstruction fidelity produced by different metasurfaces selection design methodologies in Table 1.(a) Spectrum 1～5 in Table 1;(b) Spectrum 6～10 in Table 1;(c) The reconstruction fidelity produced by different metasurfaces selection design methodologies under spectrum5;(d) The reconstruction fidelity produced by different metasurfaces selection design methodologies under spectrum10

表1 不同超构表面选择设计方法所产生的重建保真度Table 1 The reconstruction fidelity produced by different metasurfaces selection design methodologies

5 光谱特性的仿真验证

为获得微型光谱探测系统的完整性能指标，本文对系统的光谱特性进行了仿真验证。仿真验证的流程为：首先，采用有限时域差分(FDTD,finite difference time domain)软件仿真出具有不同结构参数与内孔图案的超构表面透射光谱，将仿真所得的多条超构表面透射光谱导出，用作压缩感知算法的测量矩阵T；随后，采用不同中心波长与带宽的光谱作为原始入射光谱f1，将原始入射光谱f1与测量矩阵相乘后得到调制光谱Y；随后，编写好压缩感知重建算法，通过所得的调制光谱Y与测量矩阵T，重建出与原始光谱f1相近的重建光谱f2；最后，采用保真度式(6)计算出原始光谱与重建光谱的保真度F。

首先，采用窄带光谱验证系统感知自然界中单色光的能力，将原始入射光谱设为中心波长为560 nm、带宽为1.8 nm 的窄带光谱，图5(a)为窄带光谱下的重建效果，图5(b)是图5(a)的中心波长附近的放大图像。如图5(a)和5(b)所示，重建后的光谱与原始光谱吻合，系统能准确感知窄带光谱。随后，本文仿真验证了系统的光谱分辨率，将原始入射光谱设为中心波长间隔分别为2 nm 和3 nm、带宽为1.8 nm 的双峰光谱，图5(c)和5(d)为双峰光谱下的重建结果。如图5(c)和5(d)所示，系统能较好地分辨中心波长间隔为3 nm 的双峰光谱，不能分辨中心波长间隔为2 nm 的双峰光谱，这表明系统的光谱分辨率约为3 nm。随后，本文验证了系统感知宽带光谱的能力，将入射光谱设定为不同中心波长和带宽的宽带光谱，图5(e)和5(f)为宽带光谱下的重建结果。如图5(e)和5(f)所示，系统对宽带光谱具有较好的重建效果，这表明系统能对宽带光谱进行感知重建。为测试不同数量的超构表面对重建保真度的影响，图5(e)和5(f)还分别描述了超构表面数量M为36、49 和64 时宽带光谱的重建效果。如图5(e)和5(f)所示，随着结构数量增加，重建光谱的保真度也相应增加，这是因为随着超构表面的数量增加，其透射光谱的随机性也增加，重建算法对噪声的鲁棒性也相应增强。

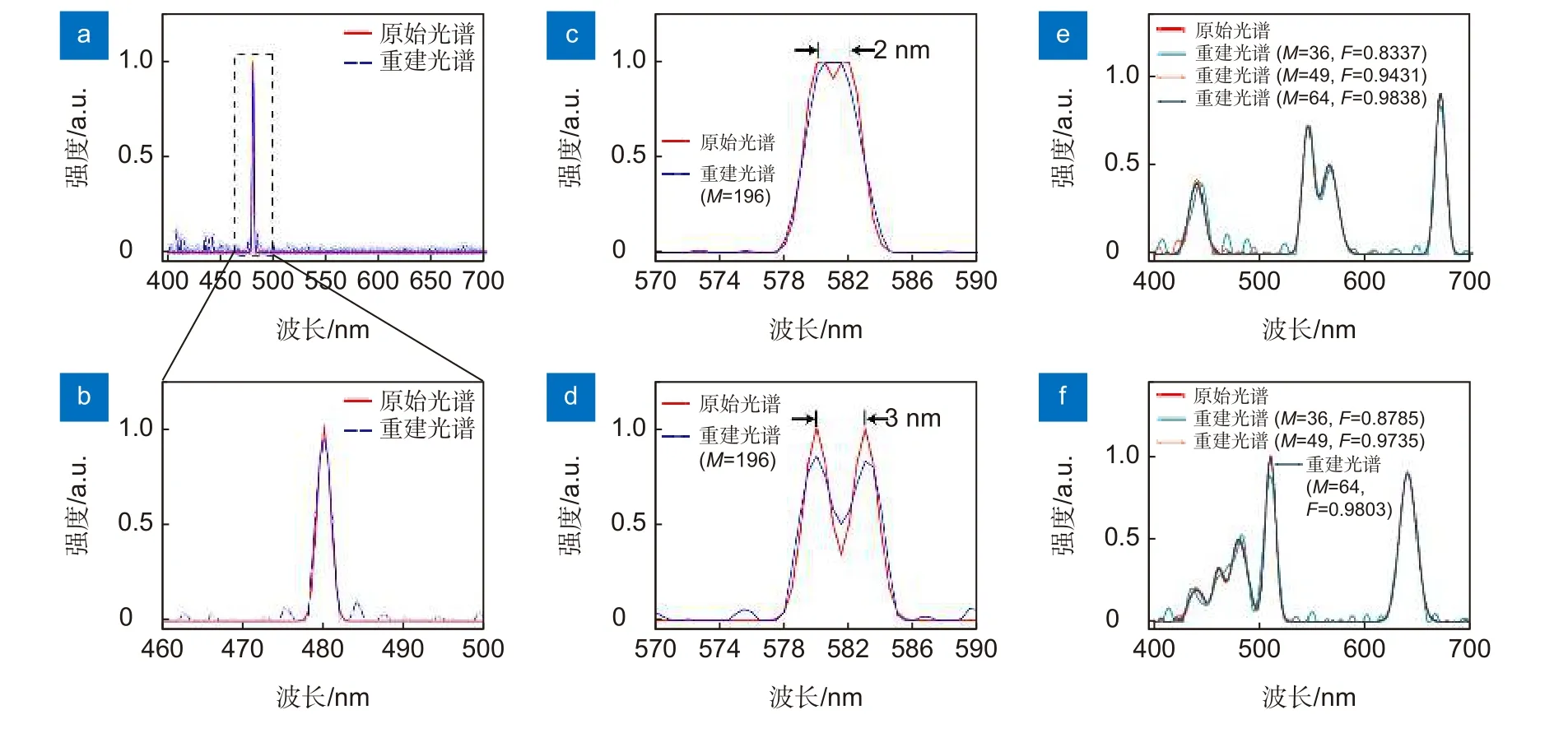
图5 光谱特性仿真验证。(a) 中心波长为560 nm，带宽为1.8 nm 的入射光谱和重建光谱；(b)图5(a)中心波长处的放大图像；(c) 中心波长间隔为2 nm 的光谱分辨率仿真验证；(d) 中心波长间隔为3 nm 的光谱分辨率仿真验证；(e) 不同结构数量M 下，宽带光谱1 的重建光谱及重建保真度；(f) 不同结构数量M 下，宽带光谱2 的重建光谱及重建保真度Fig.5 Spectral characteristic simulation verification.(a) Incident spectrum and the reconstructed spectrum with a central wavelength of 560 nm and a bandwidth of 1.8 nm;(b) Enlarged images around the central wavelength in Fig.5(a);(c) Spectral resolution simulation verification with a central wavelength interval of 2 nm;(d) Spectral resolution simulation verification with a central wavelength interval of 3 nm;(e) Reconstruction spectrum and reconstruction fidelity of broadband spectrum 1 under different number of structures M;(f) Reconstruction spectrum and reconstruction fidelity of broadband spectrum 2 under different number of structures M

最后，本文将维度为1392×1083×601 的图像光谱信号设定为原始光谱，其中1392×1083 为图像纵横比，601 为波长采样点的个数，该图像光谱信号数据来源于跨学科计算视觉实验室[46]，原始图像光谱信号如图6(a)所示。采用图3 的方法，在现有的超构表面透射光谱数据库中，依据所提出的方法和随机选择设计方法，分别选择出了两组不同的超构表面。原始图像光谱信号通过两组不同的超构表面后被调制，被调制的信号经压缩感知算法恢复后可得到两组重建的图像光谱信号，其中按照相关性均值[0.1～0.3]选择出的超构表面结构所产生的重建图像光谱信号如图6(b)所示。为表征系统感知图像光谱信号的能力，本文展示了四个色块的重建结果，结果示意图如图6(c)所示，其中重建光谱1 为依据相关性均值[0.1～0.3]选择的超构表面所产生的，重建光谱2 为随机选择出的超构表面所产生的。如图6(c)所示，在所选择的四个色块，重建光谱1 的保真度始终高于重建光谱2 的保真度，这表明相较于随机选择设计方法，本文所提出的超构表面设计方法，能在一定程度上提高图像光谱信号的重建质量。

图6 图像光谱信号感知验证。(a) 原始的图像光谱信号[46]；(b) 重建的图像光谱信号；(c) 在不同色块下，两种超构表面设计方法所产生的光谱信号重建保真度。其中重建光谱1 由按照相关性均值[0.1～0.3]所选择出的超构表面结构所产生，重建光谱2 由按随机选择出的超构表面结构所产生Fig.6 Image spectral signals perception verification.(a),(b) Original and reconstructed image spectral signals respectively[46];(c) Reconstruction fidelity of spectral signals generated by different metasurface design methods under different color blocks.The reconstructed spectrum 1 is produced from the metasurface structures selected using the average correlation value interval [0.1～0.3],and the reconstructed spectrum 2 is produced from the randomly selected metasurface structures

如表1 与图6 的保真度数据所示，表1 中的保真度增幅高于图6 图像光谱的保真度增幅，经分析后发现，图像光谱的重建光谱在400 nm～500 nm 范围内有较大杂散波，而与图5(e)～5(f) 类似的表1 的宽带重建光谱在此波长范围内并无太大杂散波，这表明微型光谱探测系统对表1 宽带光谱的兼容性优于对图6 图像光谱的兼容性，兼容性的差异导致了表1 中的保真度增幅高于图6 图像光谱的保真度增幅。

6 结 论

本文完成了超构表面透射光谱的仿真设计，并对一种基于超构表面的微型光谱探测系统进行了分析。针对现有基于超构表面的微型光谱探测系统设计中存在的超构表面设计缺少定量分析、无法保证重建质量最优的问题，本文定义了超构表面透射光谱的相关性均值，定量分析了超构表面透射光谱相关性均值与重建保真度的关系，提出一种用于微型光谱探测的超构表面设计方法。为验证所提出方法的优势，本文从众多光谱选择了10 条宽带光谱及图像光谱进行展示。相较于随机选择设计方法，本文所提出方法能提高选定的10 条宽带光谱与图像光谱信号的重建质量，宽带光谱重建保真度的增幅可达13.17%，图像光谱信号的重建保真度也得到一定的提升。此外，本文还仿真验证了基于超构表面的微型光谱探测系统的光谱特性，该系统对宽带、窄带光谱和图像光谱信号都具有较好的重建效果，具有结构紧凑、体积小的优势。