基于相变材料GST 的圆二色性可调谐外在手征超表面设计

史卓琳，贺景琳，王金金，邵汉儒，董建峰

宁波大学信息科学与工程学院，浙江 宁波 315211

1 引 言

手征是一个几何概念，是指物体不能通过旋转、平移等操作与其镜像重合。手征超表面[1]作为超表面研究的一个重要分支，具有天然材料难以实现的物理性能，例如巨大的圆二色性(circular dichroism,CD)和强旋光性(optical activity,OA)[2]、不对称传输(asymmetric transmission,AT)[3]和负折射率[4]。与传统的手征超表面不同，外在手征超表面[5]的结构是对称的，其手征电磁响应由光的倾斜入射和非手征结构的共同作用产生，非手征结构与斜入射波结合产生了一种无法通过任何旋转和平移等操作与其镜像重合的手征几何排列。外在手征超表面不仅具有与手征结构相同的电磁特性，还可以通过控制入射角来操纵电磁波，在一定程度上减少了某些超表面结构复杂、功能单一、带宽窄的通病，为超表面电磁特性的研究提供了全新的方向。目前，人们已经对超表面的外在手征特性进行了广泛研究，然而，常规的超表面一旦被制造出来，其功能也随之被固定。因此，许多学者一直致力于研究可调谐的外在手征超表面，其在光学操纵方面尤为灵活，并且可以实现多种功能[6]。通过在超表面设计中加入可调材料如相变材料(phase change material,PCM)[7]、石墨烯、液晶等，再加上外部激励的作用，就可以调节超表面的电磁特性，实现对电磁波的波前调控，在传感器、偏振器、探测器等光学器件中有潜在应用[8-10]。

基于硫系化合物的相变材料(PCM)特别是锗-锑-碲化合物 (GexSbyTez,GST)[11]已被证明具有非易失性，同时具有良好的热稳定性、高循环性和开关特性[12]，可用于实现各种光学功能的动态调谐。作为一种常见的相变材料，Ge2Sb2Te5(GST225，本文后面简称GST)通过电或光激励可以在非晶态和晶态之间进行非易失、快速和可逆的切换。GST 在这两种状态下的介电常数有极大的差值，并且具有长期稳定性[13]。基于相变材料的可调谐超表面是当前的研究热点之一。圆二色性(CD)作为手征超表面的一个重要性质，与相变材料GST 相结合就可以实现对超表面手征特性的主动控制，在宽带圆偏振器、偏振成像和圆二色性开关[14]等领域具有广泛的应用。

2008 年，Plum 等[5]首次证明了光倾斜入射谐振环时可以在微波段产生较强的圆二色性(CD)和旋光性，这种现象是由结构的外在手征特性引起的[15-16]。2012 年，Feng 等[17]从理论上研究了斜入射光线引起的层状外在手征超表面的圆二色性，该结构获得了0.365 的CD 值。2013 年，Lee 等[18]提出了一种在可见光范围内有较强圆二色性的外在手征超表面。同年，Cao 等[19]研究了一种金属-GST-金属手征超表面，随后，他们[20]还研究了由椭圆纳米孔阵列(ENA)组成的可调外在手征超表面，该结构实现了多波段圆二色性调谐，这是由GST 的巨大光学性能差异造成的。2015 年，Yin 等[21]将Ge3Sb2Te6(GST326)与手征结构相结合，实验证明了工作在中红外波段的第一个可调谐手征超表面。2018 年，Ardakani 等[22]提出了一种基于V 型纳米结构的外在手征超表面，其在红外波段获得了多波段圆二色性。2020 年，Dong 等[14]设计了一种CD 调谐范围达到38.7%的多层堆叠结构。最近，Hao 等[23]首次报道了太赫兹波段的可调谐外在手征超表面，当光倾斜入射到该超表面时，可获得的CD 最大值为0.58。尽管如此，目前尚未有针对光频段具有外在手征特性的可调谐超表面的研究报道。

本文提出了一种在光频段实现巨圆二色性的可调谐外在手征超表面，它由两个相同的银(Ag)方形开口谐振环和夹在中间的GST 薄膜组成，相比现有文献报道的具有外在手征特性的可调谐超表面，该超表面的CD 更大，调谐范围更宽。在50 THz～300 THz的频率范围内，GST 为非晶态时，该外在手征超表面的CD 值最大可达0.85。由于晶态GST 在该频率范围内有较大的损耗，外在手征响应被削弱，晶态时的CD 值最大为0.52。在外部激励下，GST 在两种相态(非晶态-晶态)之间切换，并使CD 的频率调谐范围达到了70 THz 左右。还研究了入射角和结构参数对圆二色性的影响。本研究工作为实现相变材料与外在手征超表面相结合来实现手征特性的动态调谐提供了一条途径。

2 设计原理与方法

本文提出的超表面结构如图1 所示，两个相同的银(Ag)方型开口谐振环和中间的GST 层组成了三层外在手征超表面，其中前后两个Ag 方型开口谐振环的方向和结构参数都相同。该超表面的具体参数为：p=600 nm，l=500 nm，l1=400 nm，l2=110 nm，l3=90 nm，t1=10 nm。Ag 在光学应用中具有优异的表现[24]，计算时其光学参数采用有损耗的Drude 模型[25]，取等离子频率ωp=2π×2175 THz，碰撞频率ωc=2π×4.35 THz。GST 层的厚度t为10 nm。在本文中，我们研究的频率范围为50 THz～300 THz，转换成波长范围为1 μm～6 μm。使用电磁仿真软件CST Studio Suite 模拟得到S 参数曲线以及电场分布，在x轴和y轴方向上选择unit cell 周期性边界条件，在z轴方向上则选择开放式边界条件。

图1 设计的外在手征超表面结构阵列及其单元结构示意图。(a) 外在手征原理和斜入射方向；(b) 单元结构；(c) 具体结构参数Fig.1 Schematic diagram of the designed extrinsic chiral metasurface structure array and its unit cell structure.(a) The principle of extrinsic chirality and the direction of oblique incidence;(b) Unit cell structure;(c) The specific structural parameters

左旋圆极化(LCP)波和右旋圆极化(RCP)波的传输特性可以用琼斯矩阵表示为[26]

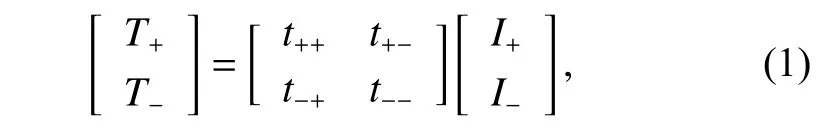
其中：下标“+”和“-”分别表示RCP 和LCP 波，I为入射波振幅，T为透射波振幅。t++和t- -分别表示RCP 和LCP 波的传输系数，t+-和t-+表示RCP 和LCP 波之间的转换系数。

由于RCP 波和LCP 波透射率不同而导致的圆二色性(CD)可以表示为[2]

根据实验数据[27-28]可以得到GST 在0～14 μm 波段内的介电常数，如图2(a)所示，其中1 μm～6 μm(50 THz～300 THz)部分用灰色阴影标出。可以发现，在50 THz～300 THz 的频率范围内，GST 为晶态(cGST)和非晶态(aGST)时的介电常数有较大差异。晶态GST 的介电常数实部(蓝色粗线)介于30～40 之间，一直大于非晶态(橙色粗线)。随着波长的增大，晶态GST 的介电常数虚部(绿色细线)不断增大，即损耗不断增大。当GST 为非晶态时，其介电常数虚部(红色细线)基本为0，即几乎没有损耗。也就是说，晶态GST 与非晶态相比有相对较大的损耗。通过电或光激励可以使GST 发生相变，同时，这个变化过程是可逆的。改变GST 的状态就可以改变中间层的介电常数，从而对超表面的外在手征特性进行调谐。

图2(b)展示了GST 晶态与非晶态的相变过程。GST 的初始状态一般为非晶态，通过各种方式如使用脉冲激光照射或外加电压将其加热超过160 ℃可使其发生相变。GST 可以在微秒级的时间内相变，并且这个变化是可逆的。相反，给已经处于晶态的GST升温至640 ℃使其熔化，再迅速冷却，晶态GST 就会转变成非晶态。同时，这个过程是非易失的，即使撤去外部激励并回到室温环境，GST 仍可长时间保持相变后的晶态或非晶态[8,13]。

图2 (a) GST 为非晶态和晶态时的介电常数[27-28];(b) GST 晶态与非晶态的相变过程[8]Fig.2 (a) Dielectric constants of amorphous and crystalline GST [27-28];(b) Sketch of phase transitions between crystalline and amorphous phases of GST [8]

3 数值模拟结果与讨论

本文数值模拟了GST 分别为晶态和非晶态时圆极化波从前向入射到该超表面时的透射特性。图3(a)和3(b)给出了在入射角θ=50°，入射投影角φ=0°时的透射系数幅度谱，其中θ=50°，φ=0°为大量数值模拟后最优化的角度。从图3(a)可以看出，当GST为晶态时，在f=130 THz 附近，交叉极化透射曲线t+-和t-+基本重合，t++取最大值0.72，t- -为0.05，t++和t--出现明显差异,这表明在该频率点附近必然存在明显的圆二色性(CD)效应。当θ=50°，φ=0°时，GST 为非晶态时的透射系数如图3(b) 所示。在f=200 THz 附近，交叉极化透射曲线t+-和t-+基本重合，并且小于0.2，t++=0.93，t- -=0.05，同样出现较大差异。对比图3(a)和图3(b)，可以发现GST 相变后，共振向低频方向移动，出现了大约70 THz 的大频率调谐，带宽和透射峰值均变小，这与晶态时的GST 在该频段有较大损耗有关。

图3 GST 为(a)晶态和(b)非晶态时的透射系数Fig.3 Transmission coefficients for (a) crystalline and (b) amorphous states of GST

为了更清晰地阐明该结构的圆二色性，我们通过式(2)计算了该超表面分别在GST 处于晶态和非晶态时的CD 谱，如图4 所示。可以看出，当圆极化波倾斜入射到该超表面时，在谐振点附近产生了较大的CD 效应，并且可以清楚地观察到圆二色性的调谐。图4 中黑色实线是GST 为非晶态时的圆二色性参数曲线，此时在6 个频率点形成了强烈的CD 共振峰或共振谷，在频率f=200 THz 时，CD 值最大可达0.85。红色虚线是GST 为晶态时的圆二色性参数曲线，在频率f=130 THz 时，CD 值最大可达0.52。当GST由非晶态转变为晶态时，圆二色性峰值会降低，这是由于晶态时的损耗较大，外在手征响应被削弱。同时，我们观察到当GST 的状态改变时，CD 光谱变得可调，从而可以用来开启或关闭外在手征响应。例如，当GST 从晶态切换到非晶态，CD 在f=130 THz 附近由0.52 下降到0 左右，相当于关闭了外在手征响应。光频域对等离子体器件来说是一个重要的光谱区域，光频域的可调外在手征特性是至关重要的。

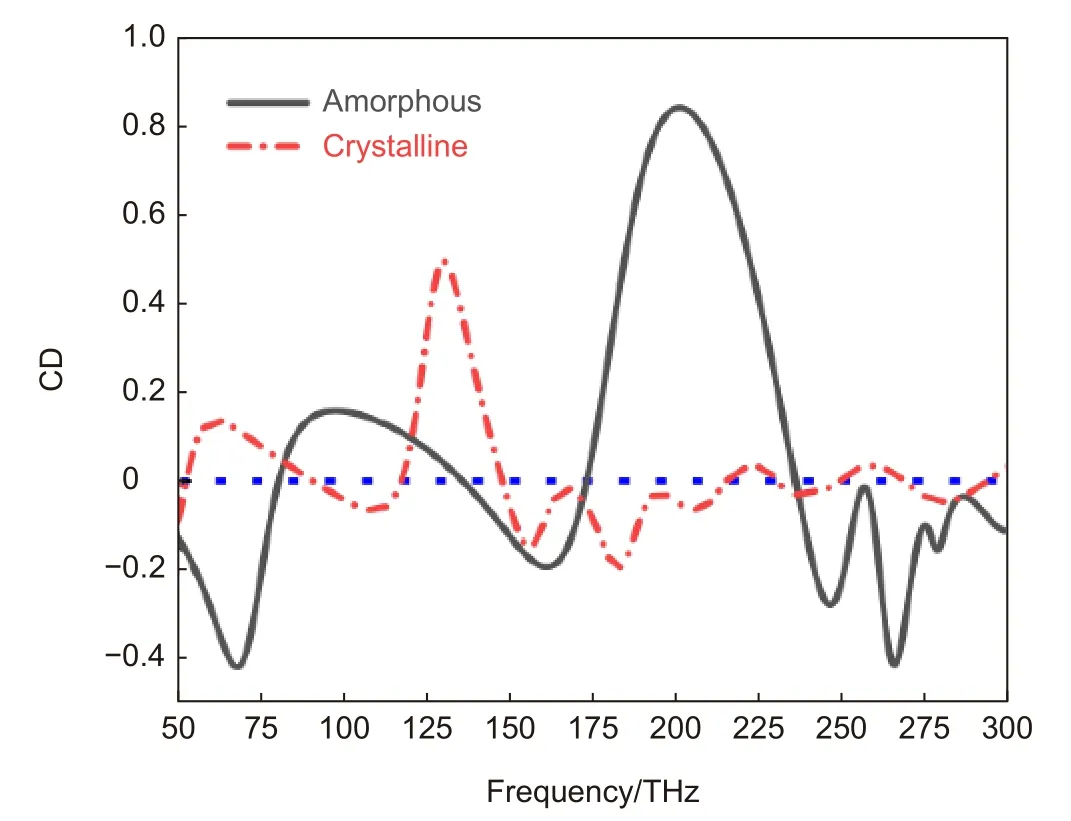
图4 在θ=50°，φ=0°时，GST 为非晶态和晶态时的CD 谱Fig.4 The CD spectra for amorphous and crystalline states of GST at θ=50° and φ=0°

根据Plum 等人对外在手征超表面的研究[5]，在一定范围内，手征特性会随着入射角的增大显著增大。然而，当入射角增大到一定程度时，手征特性将会呈现下降的趋势。图5(a)和5(b)是在φ=0°，GST 分别为非晶态和晶态时，θ以10°为间隔从0°增加到90°的CD 参数曲线图。可以看出，无论GST 处于晶态还是非晶态，当θ=0°时，CD 在所有频段内均为0，即垂直入射时，该结构没有内在手征特性。随着角度θ的增大，CD 的峰值先增大后减小，即CD 效应先变得明显，随后逐渐变弱，且基本没有频移。无论GST 是晶态还是非晶态，θ对圆二色性参数曲线的影响基本相同。在θ=50°，GST 为非晶态时入射投影角φ对圆二色性CD 曲线的影响如图5(c)所示。随着φ的增加，CD 曲线的幅值明显下降，直至φ=90°时下降为0，并且逐渐向低频处移动。在θ=50°，GST 为晶态时，从图5(d)发现圆二色性参数的幅值同样逐渐减小，当φ=0°时有最大值0.52，φ=90°时减小为0，并且逐渐红移。因此，无论GST 是晶态还是非晶态，入射投影角度φ对圆二色性参数曲线的影响也基本相同。

图5 当φ=0°，(a) GST 为非晶态和(b)晶态时不同入射角θ 的CD 参数曲线；当θ=50°，(c) GST 为非晶态和(d)晶态时不同入射投影角φ 的CD 参数曲线Fig.5 The curve of CD parameters with different incidence angles θ in GST (a) amorphous and (b) crystalline states when φ=0°;The curve of CD parameters with different incidence projection angles φ in GST (c) amorphous and (d) crystalline states when θ=50°

本文还研究了GST 为非晶态时圆二色性对结构几何参数的依赖关系。如图6 所示，当圆极化波倾斜入射(θ=50°，φ=0°)到该超表面时，分别选取了GST 层的周期p和厚度t来分析二者对CD 曲线的影响。从图6(a)中可以看出，当p以20 nm 为间隔从540 nm 增加到660 nm 时，CD 曲线发生蓝移，且蓝移的程度逐渐变小，幅值逐渐增大。当p增加到一定程度时，CD 的幅值及其对应的频率基本保持不变。这是因为p变化时会改变电偶极子与磁偶极子之间的相互作用，同时，当p增加到一定程度时，对其影响变得不再明显。如图6(b)所示，当厚度t以2 nm 为间隔从10 nm 增加到20 nm 时，CD 在低频共振中出现增量，频移明显。在高频共振中出现明显的红移，幅值逐渐减小。这是因为前后两层金属之间存在耦合作用，当中间层的厚度t增加时会改变共振频率，削弱其耦合，从而导致圆二色性减弱。同时，GST 的损耗也会相应增加。因此，可以通过改变超表面GST层的厚度t和周期p来改变CD 效应。

图6 GST 为非晶态时，不同(a)周期p 和(b)厚度t 的CD 谱Fig.6 The CD spectra with different (a) period p and (b) thickness t in the amorphous state of GST layer

本文分别数值仿真了沿 -z方向看时，该结构在LCP 和RCP 波入射时的电场强度分布图。图7(a)～7(b)展示了GST 为晶态时，该结构分别被LCP 波和RCP波垂直入射(θ=φ=0°)时在f=130 THz 处的电场强度分布图。可以发现，RCP 入射和LCP 入射时的电场强度是彼此的镜像图，因此CD 响应为0。图7(c)～7(d)为GST 为非晶态时，LCP 和RCP 波垂直入射时在f=200 THz 处的电场强度分布图，CD 响应同样为0。这是因为电磁波垂直入射时，入射波无法与超表面结合产生手征结构，外在手征特性消失[16]。

图7 当θ=0°，φ=0°时的电场分布图。(a) 晶态GST，LCP 入射，f=130 THz；(b) 晶态GST，RCP 入射，f=130 THz；(c) 非晶态GST，LCP 入射，f=200 THz；(d) 非晶态GST，RCP 入射，f=200 THzFig.7 Electric field distribution when θ=0°，φ=0°.(a) Crystalline GST,LCP incidence,f=130 THz;(b) Crystalline GST,RCP incidence,f=130 THz;(c) Amorphous GST,LCP incidence,f=200 THz;(d) Amorphous GST,RCP incidence,f=200 THz

图8(a)～8(b)给出了GST 为晶态时，LCP 波和RCP 波倾斜入射(θ=50°，φ=0°)时的电场强度分布图，此时f=130 THz 处的CD 为0.52。从图中可以看出，RCP 波入射时，方型开口谐振环四角出现了明显的电场响应，而LCP 波入射时的电场响应很小，这意味着该结构对不同旋向的圆极化波具有选择性。即LCP 和RCP 波在方型开口谐振环夹角处的谐振模相位产生强烈干涉，导致这两种圆极化波入射时的不同透射率[22]。这是因为振荡的磁偶极子产生了一个相位滞后的波分量，对原有的极化方向起到阻碍的作用，使其偏振面发生了旋转[16]，从而大大削弱了RCP 波的透射率，而LCP 波的透射率并未受到太大影响，因此获得明显的透射圆二色性。图8(c)～8(d)给出了GST 为非晶态时，不同圆极化波倾斜入射(θ=50°，φ=0°)时在f=200 THz 处的电场强度分布图。从图4 可以得到此处的CD=0.85，比GST 为晶态时大很多。如图8(c)～8(d)所示，RCP 波入射时，在方型开口谐振环的四角处都有较强的电场，而LCP 波入射时极弱。对比图8(a)～8(b)，8(c)～8(d)可以看出，非晶态时分别被LCP 和RCP 波入射产生的电场强度的差异比晶态时的差异大，因此GST 为非晶态时的圆二色性强于晶态。

图8 当θ=50°，φ=0°时的电场分布图。(a) 晶态GST，LCP 入射，f=130 THz；(b) 晶态GST，RCP 入射，f=130 THz；(c) 非晶态GST，LCP 入射， f=200 THz；(d) 非晶态GST，RCP 入射，f=200 THzFig.8 Electric field distribution when θ=50°，φ=0°.(a) Crystalline GST,LCP incidence,f=130 THz;(b) Crystalline GST,RCP incidence,f=130 THz;(c) Amorphous GST,LCP incidence,f=200 THz;(d) Amorphous GST,RCP incidence,f=200 THz

本文给出的均是在没有衬底情况下的数值模拟结果，如果加上衬底材料(例如加一层厚度为300 nm的MgF2)，将会对超表面的圆二色性产生一定的影响，最大CD 值将会从0.85 减小为0.80，但总体来说影响不大。另外，如果上下两层开口谐振环没有完全对准，圆二色性也会有所减小。

4 结 论

本文设计了一种由Ag-GST-Ag 组成的三层对称方型开口谐振环结构，当圆极化波倾斜入射时，实现了与手征结构相同的电磁特性，并通过数值方法证明了超表面的圆二色性可调。在50 THz～300 THz 的频率范围内，GST 为非晶态时获得了0.85 的巨圆二色性。与相变前相比，GST 为晶态时该结构的CD 谱发生了巨大红移，实现了70 THz 左右的频率调谐。进一步的研究表明，改变入射角和GST 层的几何参数可以对圆二色性进行调控。还研究了不同相态时在谐振点的电场分布。相变材料GST 与外在手征超表面结合，几何结构简单，在光频段的高效偏振调制器件、圆偏振器和偏振滤光器等器件上有潜在的应用前景。