车载毫米波雷达时域测高技术研究

沈文皓，杨明磊，郭俊磊，胡晓宇，刘 楠

(西安电子科技大学 雷达信号处理国家重点实验室，陕西 西安 710071)

毫米波雷达具有探测距离远、全天时全天候等优势，是汽车“高级驾驶辅助系统”(Advanced Driving Assistance Systems，ADAS)中必不可少的传感器[1]。然而，传统车载毫米波雷达一般不具备测高能力。同时，车载毫米波雷达安装位置较低，俯仰维波束宽度较宽，低仰角目标的回波可能通过多条路径到达接收天线并产生干涉现象，即存在多径效应，这对仰角估计有较大影响。一般地，实现多径与直达信号的分离有两种方法：从角度维或从距离维分离。从角度维看，目标直达信号与多径信号之间的夹角远小于天线俯仰维波束宽度，从角度上分离需要较大孔径；从距离维看，多径与直达信号的波程差在大多数情况下都小于现阶段毫米波雷达的距离分辨力，从距离上分离也很困难。因此，如何处理多径效应是车载环境下无法避免的难题。

目前，针对多径效应下的信号模型、地面反射特性的研究主要集中在米波段，毫米波段的研究则较少。在障碍检测领域，DIEWALD等[2]提出在驾驶卡车等慢速情况下，利用多径效应进行桥梁识别的算法，并根据桥梁与静止障碍物所处的高度范围不同将两者进行了区分。针对低小目标，LARIBI等[3]引入RALEX算法分离多径与直达信号，在距目标5 m内实现了一定精度的高度测量；之后，他们建立了车辆运动的几何模型并推导出目标高度测量公式，使用多普勒锐化和3D-RALEX算法进行数据处理[4]。OLBRICH等[5]基于高墙体目标存在多个散射点和多条传播路径，会产生接收信号的叠加，而低墙体目标不具备这些特征，从空域角度提出了一种对高低目标进行分类的方法，但这种方法需要多根不同高度的天线。针对多径效应可能产生虚假目标的情况，LIU 等[6]通过分析多径和直达波的波程差，提出了一种在中程有效去除虚假目标的方法。此外，部分毫米波厂家提出了利用多个毫米波雷达板进行级联产生大量虚拟阵列以实现环境感知及成像的解决方案[7]，但其成本高、结构复杂，始终是在车载环境中应用时需解决的难题。

笔者提出了一种利用汽车运动和多径效应的时域单天线目标高度测量方法，不需要额外增加其他天线和通道，实现简单。笔者详细分析了对测高范围及精度产生影响的因素，从中总结了模型规律。针对实际场景中可能存在的障碍物和人等目标的情况，利用角反、小车等工具模拟实际场景，通过77 GHz线性调频连续波雷达采集数据进行分析和处理，验证方法可行性，并提出了一系列优化建议。

1 信号模型

1.1 多径效应存在的条件

一般地，在驾驶环境下雷达发射的电磁波存在由地面反射造成的多径效应。图1给出了多径效应的模型示意图。假设毫米波雷达放置于A点处，距离地面高度为hs，高度为ht的目标T到雷达的直达距离为Rd，到天线水平距离为R。由于天线俯仰维波束较宽，雷达发射的信号除直接沿A—T传播并返回的直达信号A—T—A之外，还存在经过地面反射的路径为A—B—T—A的多径信号到达接收天线。因此，雷达接收到的信号为直达波和多径信号的叠加信号。

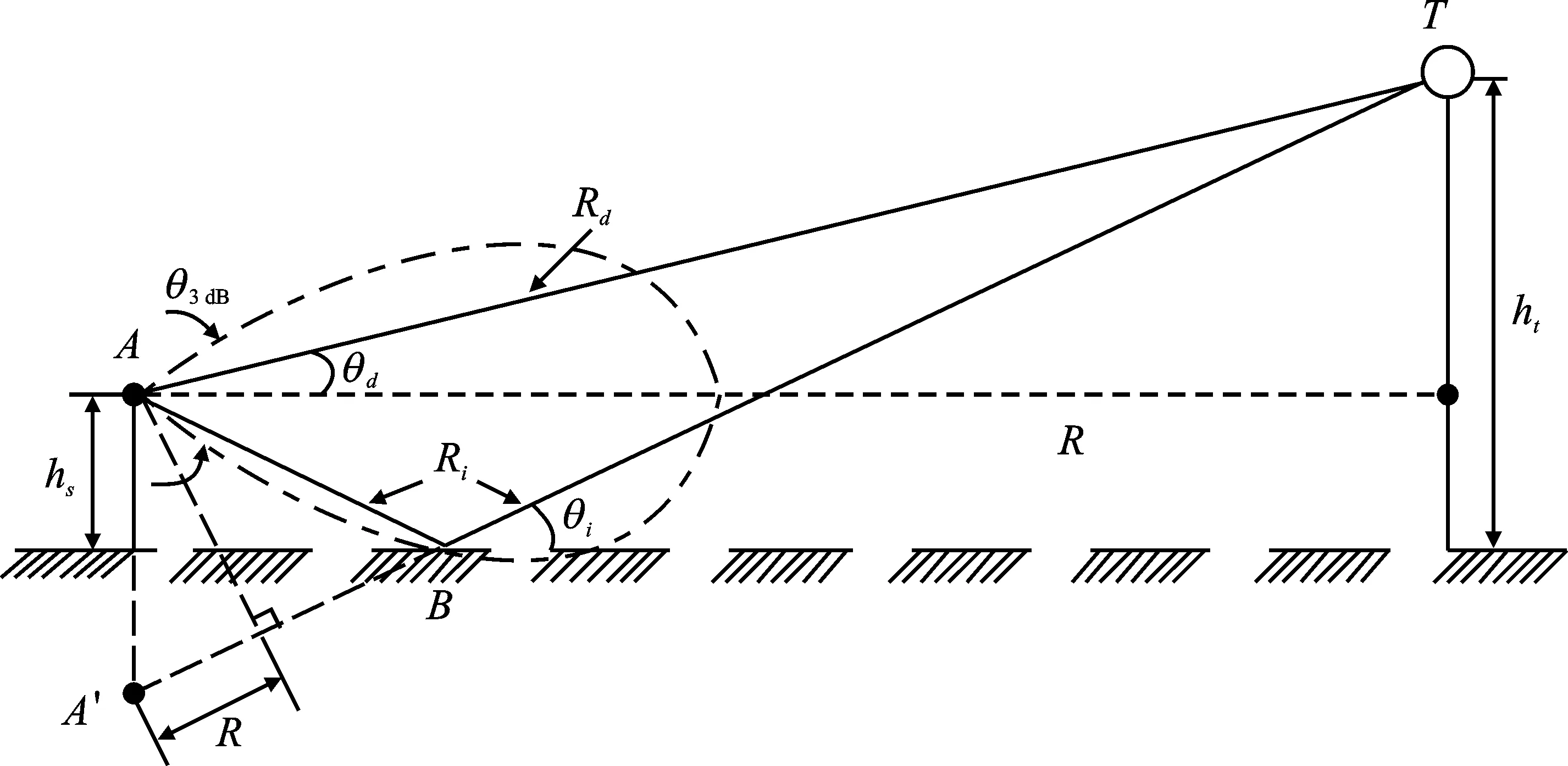
图1 毫米波雷达多径效应数学模型

由此，假设多径效应存在的前提是多径信号经地面反射后仍能从接收天线的俯仰维3 dB波束宽度内进入天线。当接收天线俯仰维的波束指向水平面时，通过几何关系可得能接收到多径信号的距离最小值Rlmin：

(1)

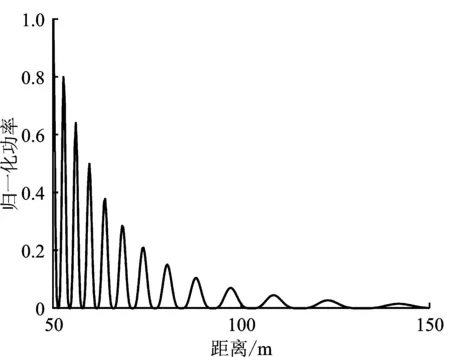
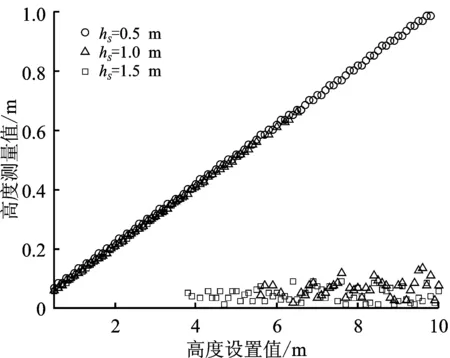
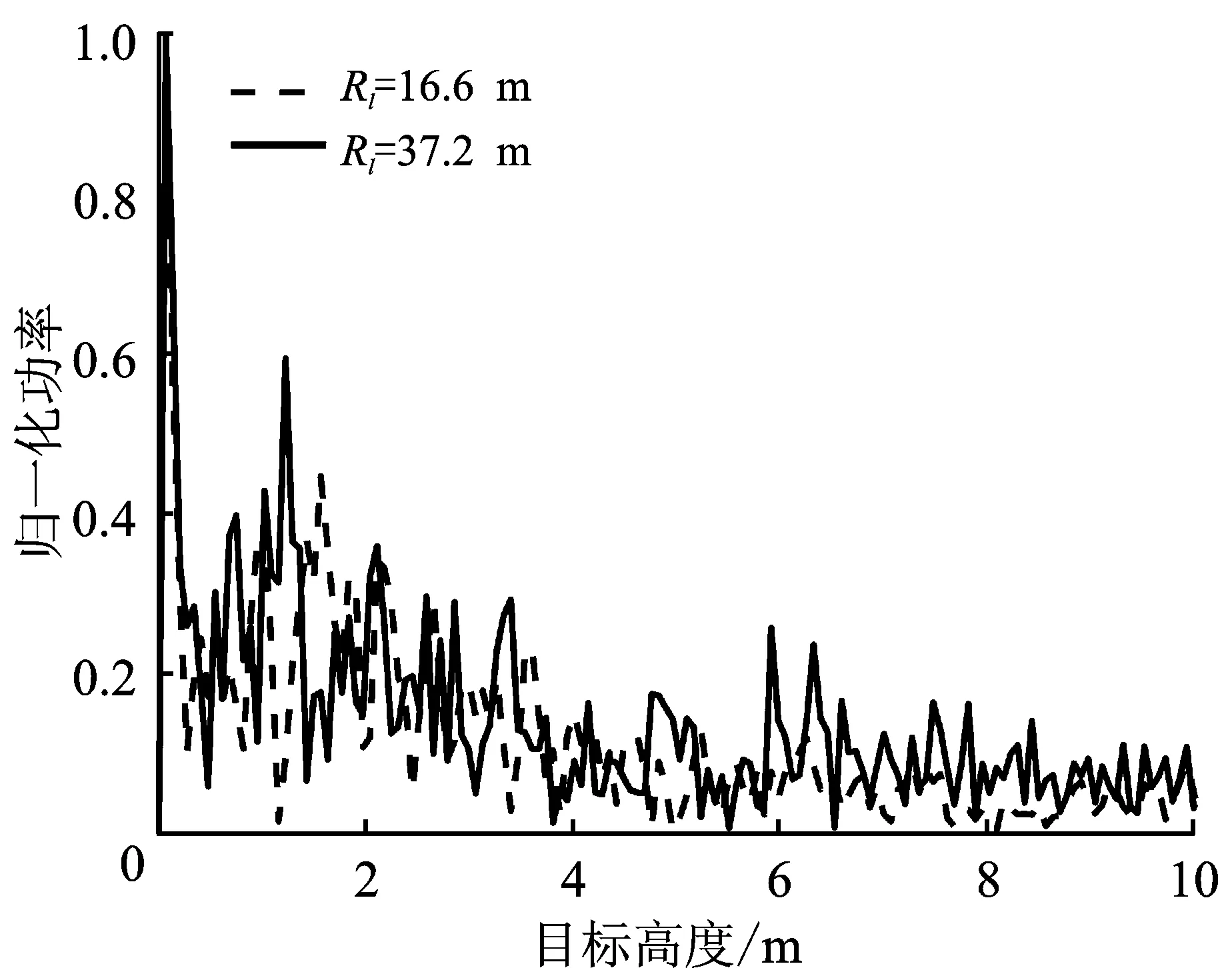
其中，hs为天线高度，θ3 dB为3 dB波束宽度。当R

0≤ht≤Rtan(θ3 dB/2)-hs。

(2)

当雷达天线俯仰维3 dB波束宽度θ3 dB=28°，根据式(2)计算可知雷达安装高度hs在0.60 m时，对于高度ht≤4.00 m的目标，在距离18.45 m之外都需要考虑多径效应的影响，如表1所示。随着目标高度和雷达安装高度越高，产生多径效应的临界距离就越大。可以认为，在车载环境中，绝大多数存在潜在危险的目标从始至终存在多径效应，而桥梁、广告牌等高目标的多径效应在一定距离内也是存在的。

表1 不同雷达安装高度和目标高度下，多径效应存在的边界距离表 m

1.2 数学模型

对于单根天线，直达信号和多径信号到达接收天线处存在波程差，这会导致直达信号和多径信号存在相位差，不同的相位差又会导致不同的信号叠加效应，最终使接收天线的接收信号能量不同。这种叠加效应导致接收功率在时域上存在一定的周期性，并且这种周期性与目标的高度信息相关。因此，可以利用汽车运动时，距离目标远近不同时直达信号和多径信号叠加产生的幅度变化的周期性来测量目标的高度。

假设目标是单散射点，目标处的直达波与多径波场强分别是Ed，Ei；雷达辐射功率是Pt，直达波和反射波对应的天线增益分别是Gd，Gi；直达波与反射波的波程差为ΔR；θd和θi分别为天线对目标的仰角和地面的反射角；地面反射系数的模值与相角分别为ρ、φ；η0表示自由空间的本征阻抗。由雷达方程[8]，直达波和多径波在目标处的功率密度可分别表示为

(3)

(4)

其中，Δφ表示直达波与多径波的相位差。由此可设目标处直达波和多径波场强分别为

(5)

当天线高度和目标高度远小于目标与天线的水平距离时，即hs/t≪R，地面反射角θi很小。由几何关系sinθi=hs/AB，可得hs≪AB≪Rd/i。此时，直达波和反射波可以近似看作平行波。在上述情况下，有Rd≈Ri≈R且θi=θd，进而由sinθi=ΔR/2hs=ht/R整理得到波程差ΔR：

(6)

当天线垂直波束最大值指向水平面时，有Gd=Gi。目标所在处的合场强是入射波场强和反射波场强的矢量和，即

(7)

当电磁波为水平极化且地面反射的反射角θi较小时，反射系数的模值ρ≈1、相角φ=180°，且两者随反射角的增大变化缓慢。此时，整理式(7)得

(8)

由此可得天线处的接收功率Pr，即多径效应下的雷达方程为

(9)

(10)

(11)

式(11)指出了目标高度ht与天线高度hs和波长λ有直接关系，同时与回波的主要频率分量fh呈正比。

2 毫米波雷达时域测高方法

汽车行进过程中毫米波雷达采样过程如图2所示。假设汽车以速度v向着目标前进，雷达已跟踪上目标，采样帧周期为T0。这样每隔一段距离Rs=vT0，雷达即可获得一次目标的回波能量，记第m次采样的回波功率为Pm，称Rs为距离采样间隔。通过上述采样过程，可以获得用于高度测量的距离采样区间[Rl，Rr]范围内的多个位置的目标回波功率，其中Rl为距离采样下边界，Rr为距离采样上边界。

图2 汽车靠近目标过程中的距离采样图

图3 时域测高算法流程图

2.1 测高流程仿真

对多径条件下的毫米波雷达目标回波模型及时域测高方法进行仿真分析。假设天线高度hs=0.6 m，目标高度ht=3.0 m，距离采样区间[Rl，Rr]=[50 m，150 m]，距离采样间隔Rs=0.3 m，模拟汽车靠近目标的过程，记录目标的回波功率和距离，再将距离变换到距离倒数上，得到如图 4所示的曲线。

(a) 随距离的变化

从图4可以看出，回波功率曲线的频率随距离增大而变小，但在距离倒数轴上是常数。此时，通过线性插值的方法，可以使原本在距离倒数上非均匀的采样点均匀化，插值前后对比如图5(a)所示。对插值后的曲线进行FFT，获得其频谱并变换为高度谱后如图 5 (b)所示。图中除直流外存在两个分量，将主要频率分量对应的频率值转化为高度，即可获得目标高度测量值ht=3 m，与设置值吻合。

(a) 插值前后对比

2.2 高度测量影响因素分析

目标回波幅度中的距离项、天线高度、距离采样区间及上下边界等均会影响高度测量结果，笔者对这些因素进行仿真分析并总结规律，提出了去直流和幅度修正等建议。

式(10)的回波功率中存在与高度测量无关的直流分量，其在频域表现为频率中心为0的辛克函数，会对其周边的频率分量造成影响。因此，首先需要对回波进行去直流处理，可以采用减去回波功率均值的方法来实现。另外，目标回波功率与距离R4呈反比，这相当于对回波功率曲线进行了1/R4的振幅调制，使1/R较大部分的幅度远大于其他部分。然而，在距离倒数上的采样点是非均匀的，1/R较大的部分采样点更少，当采样点数过少以至于无法满足奈奎斯特采样定理时会出现失真。为了尽可能减小失真对结果的影响，对幅度中的1/R4项进行修正。图6(a)是回波功率随距离倒数变化的曲线以及修正幅度中的1/R4后的曲线对比图。修正前，失真部分恰好是幅度较大的部分，从而导致失真部分在频谱中所占的幅度也较大，可能淹没目标。这里的幅度修正可通过系统设计高通滤波器来实现，从而减小失真对测高结果的影响。进行幅度修正后，虽然低频失真仍然存在，但相较于失真部分，幅度修正显著增加了其他部分的幅度。修正前后的测高结果对比见图 6 (b)，低频噪声明显减弱，而目标分量略有增强。因此有必要对回波功率去直流和幅度修正。

(a) 修正前后对比

在车载环境中，雷达的体积一般较小，汽车前端安装雷达的位置也相对固定，通常在车牌后或挡风玻璃上方。在笔者提出的模型中，不同的天线高度hs在高度测量的范围和精度方面会有差异。在式(11)中，若以功率回波曲线的最大频率分量2ω0能够满足奈奎斯特采样定律为边界，即fs≥2×2ω0/2π，那么能够进行高度测量的最大目标频率为fmax=fs/4，其中fs为均匀插值时的插值频率，代入式(11)中可得

(12)

其中，ht max为最大可测量的目标高度，与天线高度hs呈反比。选取3组天线高度进行仿真，分别是hs=0.5 m，1.0 m和1.5 m，如图 7 (a)所示。图中高度测量结果底部产生波动处，表示高度测量产生了较大误差。从中可以看出天线高度hs越低，最大的可测量目标高度ht max就越大。同时，测高分辨单元hres与天线高度hs的关系如下：

(13)

其中，fres为频率分辨单元。图7(b)给出了测高分辨单元随天线高度变化的曲线图。天线高度hs越低，可以获得的高度测量范围越大，测高分辨单元则越差。因此需要根据实际场景中的测高需求和可用位置选择合适的雷达安装高度。

(a) 高度测量结果

在汽车靠近目标的过程中，雷达按一定帧周期T0进行采样，获取目标距离和回波功率。如果距离采样区间较大，则会导致采样点个数过少，从而使功率回波产生失真并在高度谱中引入低频噪声。为了减少低频噪声，距离采样间隔Rs应尽可能地小。但减小间隔的同时，也对雷达系统整体的实时处理速度提出了更高的要求。笔者选取两组不同的距离采样间隔Rs进行仿真对比(天线高度hs=0.5 m，目标高度ht=2.0 m)，测高结果如图 8(a)所示，可见Rs=0.5 m时高度谱中低频噪声明显大于Rs=0.2 m时的低频噪声。

(a) 不同距离采样间隔

3 实测数据验证

为验证该方法的可行性，利用遥控小车对一定高度的角反射器目标进行了实测，实验场景设置如图9所示，天线高度hs=1.6 m，目标高度ht=1.3 m，从距离目标Rr=100 m处开始采样，距离采样间隔约为Rs=0.12 m。实验选用TI公司毫米波雷达AWR1843套件，具体参数如表2所示。

表2 雷达参数表

图9 实验场景图

图10给出了回波功率幅度随距离和距离倒数变化的曲线。90 m处曲线的跳变是由跟踪失败导致。图 11(b)是距离采样下边界Rl取37.2 m时的高度谱，可见除近零频处的峰值外，最高峰值对应的高度ht=1.223 m，可见方法在实际场景中具有可行性。零频处的峰值是因为无法完全修正幅度中的直流项造成的。

(a) 回波幅度-距离倒数

验证距离下边界Rl对整体测高的影响。若汽车行进采样的距离过近，低频噪声往往容易淹没目标。将采样距离下边界Rl=37.2 m与Rl=16.6 m的实验进行对比，结果如图 11 (a)所示。Rl=16.6 m时目标被淹没，无法正确测高。从幅度上来看，37.2 m～16.6 m的采样过程中，噪声分量的幅度显著提高，而目标分量的幅度没有明显提升。

对距离采样间隔Rs影响进行验证。使用相同的实验参数，并将距离采样下边界设置为Rl=37.2 m，而距离采样间隔Rs变为原来的5倍，即间隔约为Rs=0.60 m。两种情况的高度谱对比图如图 11(b)所示。从图中可以看出，当间隔Rs变为原本的5倍时，目标分量以下和附近频率分量的幅度明显增长，即低频噪声的幅度显著提高，结果与仿真分析的一致。

(a) 不同距离采样下边界

4 总 结

针对车载毫米波雷达存在多径回波的情况，笔者提出了一种使用单天线时域信息的简易测高方法。该方法主要利用地面产生的多径效应使目标回波中同时存在直达信号和多径信号，从而使不同距离下的目标回波功率存在一定周期性起伏，而这种周期性包含与目标高度相关的信息。进而，采用时域线性插值和FFT获得频谱并得到目标高度。笔者建立了毫米波段下精确的多径信号模型，分析了目标回波功率其规律及其影响因素，提出了去直流、幅度修正等优化建议，并对信号模型和测高方法进行了仿真和实测验证，结果表明了该方法的有效性。

对于高架桥、广告牌等目标，其散射点有可能是多个，散射中心位置也不确定，这对测量其准确高度带来一定的难度；另外对墙体等目标垂直方向的散射点也可能会有多个，这些带来的高度测量的影响将是后续重点研究的内容。