改进多目标蚁狮算法的WSNs节点部署策略

张 浩，覃 涛，徐凌桦，王 霄，2，杨 靖，2

(1.贵州大学 电气工程学院，贵州 贵阳 550025；2.贵州省互联网+协同智能制造重点实验室，贵州 贵阳 550025)

无线传感器网络(Wireless Sensor Networks，WSNs)由许多能量有限的传感器节点组成，通过节点之间的协作，可向用户提供精确、全面的实时监测数据。目前，无线传感器网络已广泛应用于军事、交通、环境监测等领域[1-2]，其中节点部署是影响无线传感器网络性能的重要环节之一，是整个网络可靠工作的必要条件。

节点的部署属于NP-hard完全问题，实质是一个非线性、多约束、多目标的最优化问题[3]，复杂度高不易求解，常见的求解方法有专家经验、运筹规划和启发式搜索算法等。其中启发式搜索算法在解决NP-hard问题时，具备较快的求解速度和精确度。智能算法作为一种启发式算法，在无线传感器网络节点部署问题上有广泛的应用。文献[4]提出了一种基于快速非友配排序遗传算法(NSGA-Ⅱ)的节点覆盖策略，有效增加了节点的覆盖率并降低了网络的能耗，但算法的复杂度过高。文献[5]利用遗传算法实现了节点的k连通和m覆盖，减少了节点的使用数目。文献[6]利用和声搜索算法实现了节点的最小代价覆盖，将区域的覆盖率和节点数目融合为一个目标函数，有效提高了区域的覆盖率。文献[7]将节点之间的连通性作为约束条件，覆盖率作为目标函数，添加到节点的覆盖问题中，最后利用遗传算法去解决节点的覆盖问题，有效提升了覆盖率与节点间的连通性。文献[8]提出了一种基于改进灰狼算法的无线传感网络节点覆盖策略，有效提升了区域的覆盖率。文献[9]提出了一种基于生物地理学优化算法的无线传感网络覆盖连通策略，能有效获得位置较好的节点部署位置。

尽管上述部署策略都各有优势，但主要集中在单目标优化、权重相加或约束化处理上。另外，将多目标问题转化为单目标问题求解时，一般只能求取一个最优解。而基于帕累托思想的多目标求解方法，不需要通过设置权重系数将问题转化为单目标问题，且可以同时获取多个优化解，因此被应用在多个实际问题中[10-12]。

目前，学者已提出的多种群体智能算法，如粒子群算法(PSO)[13]、灰狼优化算法(GWO)[14]、鲸鱼优化算法(WOA)[15]、麻雀优化算法(CS)[16]、蝴蝶优化算法(BOA)[17]、蚁狮算法(ALO)[18]等。其中，蚁狮算法被学者MIRJALILI在2015年提出，具备调节参数少，寻优能力强的优点；在2017年又提出了多目标蚁狮算法[19]，利用种群中个体间的支配关系寻找最优解集，并证明该算法优于一些经典多目标算法。由于该算法的优越性，被迅速应用到多个领域。文献[20]利用蚁狮算法优化(SVR)核参数，并将其应用在锂电池的寿命预测中，有效提高锂离子电池剩余使用寿命预测的准确性和鲁棒性。文献[21]运用蚁狮算法求解风电集群储能容量配置优化问题，分析了储能电池单位成本和寿命对优化结果影响，并验证了所提算法与模型的有效性。文献[22]将改进后的蚁狮算法用于无人机的三维航迹中，实现了航迹问题中的在线局部重规划。

但蚁狮算法也存在收敛精度低、易陷入局部最优的缺陷，导致在求解实际问题时容易过早收敛，不利于寻找全局最优解[23-24]。因此，笔者提出了一种改进的多目标蚁狮算法(Improved Multi-Objective Ant-Lion Optimizer，IMOALO)，首先，引入混沌初始化策略增加种群的多样性，并提出连续自适应收缩边界以增强算法的寻优能力；然后，利用时变策略对蚂蚁位置进行扰动，以增强算法跳出局部最优的能力；最后，基于帕累托最优解集的思想，将IMOALO算法应用在节点多目标部署问题中，并通过仿真验证了所提算法在无线传感网络部署应用中的有效性。

1 系统模型与问题描述

1.1 节点感知模型与连通模型

假设在面积为M×L的部署区域内，随机抛撒n个节点，其中节点集合S={s1，s2，…，si，…，sn}，si位置坐标为(xi，yi)，i=1，2，…，n，节点的感知半径为Rs，通信半径为Rc。为简化计算，将该监测区域离散化为m×l个单位正方形区域，每个子区域的中心坐标就是节点的覆盖目标，中心点的坐标集合为Cj=(xj，yj)，j∈{1，2，…，m×l}。若中心点Cj与任意节点的距离小于或等于感知半径Rs，则说明Cj被覆盖。节点si与中心点Cj的间距定义为

d(si，Cj)=((xi-xj)2+(yi-yj)2)1/2。

(1)

假设节点感知模型为布尔感知模型，中心点Cj=(xj，yj)被节点si感知的概率p(si，Cj)定义为

(2)

中心点Cj被所有节点联合感知概率定义为

(3)

若节点之间的距离小于通信半径，则两节点间连通，故节点si与节点si*之间的连通性p(si，si*)(i≠i*)可定义为

(4)

1.2 问题描述

节点的连通性与网络覆盖率是节点部署问题中两个重要的指标。如图1(a)所示，在网络中存在4个节点a、b、c、d，节点a的信息可通过节点c和d传输至基站，但当节点c出现故障时，节点a没有可传输信息至基站的路径而导致出现信息空洞；当节点b的位置移动至b1处，如图1(b)所示，b1处于节点a的通信半径内，网络中信息传输的路径增加，当节点c丧失信息传输的功能时，节点a的信息可以通过节点b1和节点d传输至基站。

(a) (b)

由图1(a)与图1(b)的对比可知，当节点b移动至b1时，网络中节点的连通性增强，但节点之间重叠的覆盖区域增加，整体的区域覆盖率下降。由此可见，网络中的覆盖率与连通度存在矛盾关系；此外，如果减少节点的使用数量，会导致网络覆盖率下降；相反地，增加节点数目，网络可达到更高的覆盖率。当同时考虑多种目标需求时，则属于多目标优化问题(Multi-objective Optimization Problem，MOP)，在多目标优化问题中，多个目标可能存在着矛盾，不存在惟一的最优解；相反地，存在着多个目标折中的最优解。

1.3 部署目标

无线传感器网络针对不同的需求，有不同的节点部署目标，当同时考虑多个目标时，传感器节点的部署问题实际是一个多目标优化问题，文中部署目标如下。

(1) 节点数目。由于传感器节点成本限制，应在监测区域内部署适当数目的节点，避免出现过多的冗余节点。

(2) 区域覆盖率。区域覆盖率RCov为感知节点集合S所对应的联合感知概率之和与区域内中心点总数的比值，即

(5)

为避免节点在优化时过于集中，对覆盖率的限制条件为RCovl≤RCov≤1，其中，RCovl为最低覆盖率。

(3)节点连通性。节点连通性是指网络中节点一跳范围之内能够与其通信的相邻节点的数量，用于描述整个网络的通信能力。同时，节点间的通信能力也是无线传感网络中信息可靠传输的基础。整个网络中节点的连接数目为

(6)

节点间连通的限制条件为∀i∈[1，n]，∃i*∈[1，n]，i≠i*，p(si，si*)=1，可保证每个节点至少能与一个其他节点连通。

1.4 多目标部署模型

根据1.3节的描述，可将部署问题用多目标优化函数表示如下：

(7)

其中，决策空间X∈[n，(x，y)]，n为部署区域中的节点数目，(x，y)为节点的位置坐标矢量。

约束条件为

(8)

其中，F(X)是目标函数；F1(X)为未被覆盖率，该值越小，说明网络的覆盖率越高；F2(X)为节点连接数目的倒数，该值越小，说明网络中存在的连接越多，数据传输越稳定。约束条件要求节点部署在监测区域内，网络覆盖率不低于最低覆盖率且节点至少可以与其他任意一个节点连通。

2 改进多目标蚁狮算法

2.1 Pareto优化模型

为了求解上述节点部署的多目标问题，利用帕累托解集的思想，求出问题的一组可行解，为不同的目标需求提供相应的方案，以最小化目标为例，MOP问题可表述为

minF(X)={f1(X)，…，fi(X)，…，fm(X)} ，

(9)

其中，F(X)为目标组合向量，X={x1，x2，…，xq}为MOP问题的解，q为变量的个数；fi(X)为其中一个目标函数，1≤j≤m，m为目标函数的数量。Pareto的相关定义[3]如下。

定义1帕累托支配：假设x是决策空间R内的可行解，对任意两个决策向量x1与x2，若满足式(10)中的关系，则说明x1可支配x2，记录为x1≻x2。

(10)

定义2帕累托非支配解：x是决策空间内的可行解，且没有解可以支配解x，则称x为非支配解。

定义3帕累托最优解集：由全部非支配解组成的集合。

2.2 多目标蚁狮算法

多目标蚁狮算法中包含以下几个角色：蚂蚁、蚁狮、外部存档和精英蚁狮，主要由以下几个步骤组成。

(1) 随机初始化种群：

xi，j=xmin，j+rand(0，1)(xmax，j-xmin，j) ，

(11)

其中，i=1，2，…，SN，j=1，2，…，D，xmax，j和xmin，j为搜索空间的上界和下界。每个解xi，j代表一个D维向量。

(2) 蚂蚁随机游走，定义为

Xi=[0，cumsum[2r(1)-1]，…，cumsum[2r(t)-1]，…，cumsum[2r(T)-1]] ，

(12)

其中，cumsum为数值累计函数，t、T分别为当前迭代次数与最大迭代次数，r(t)是0和1间的随机数，v为[0，1]内的随机数，定义为

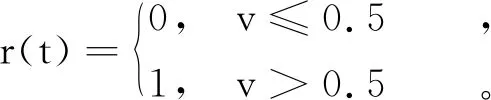
(13)

为保证蚂蚁游走的路径维持在上下界内，对其游走路径做归一化处理，定义为

(14)

(3) 通过轮盘赌选择的蚁狮和上下界共同决定蚂蚁的游走边界：

(15)

(16)

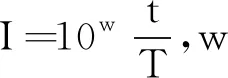
(4) 在蚂蚁被蚁狮捕捉过程中，若存在可支配精英蚁狮的个体，则该个体替换掉精英蚁狮：

(17)

将每一代中适应度最高的蚁狮作为精英蚁狮，并通过轮盘赌随机选择一只蚁狮，共同决定蚂蚁的游走路径：

(18)

(5) 重构陷阱：多目标蚁狮算法中采用一个外部存档来存储帕累托支配解集，为了获得多样性更强的解，利用小生境技术对外部存档中解的分布进行判断，使用

(19)

来定义在归档中选择解决方案的概率，当存档已满时，具有最密集邻居的解决方案将从存档中删除，以适应新的解决方案。使用

(20)

来定义从存档中删除解决方案的可能性。其中，c是一个大于1的常数，Ni是第i个解的附近解个数。在固定的半径范围内，解周围的邻居解越多，被存档的概率越低。当存档已满时，解周围存在其他解越多，被删除的可能性越大。

2.3 改进的多目标蚁狮算法

2.3.1 混沌初始化策略

混沌具有随机性、遍历性的特点，混沌初始化可提高种群的多样性，有利于算法跳出局部最优，增强全局寻优的能力。其中Fuch映射作为一种经典的混沌模型，已经被证明了优于一些经典混沌映射方法[25]，故文中选取Fuch映射去初始化种群。假设种群规模为{1，2，…，i，…，SN}，算法的空间维数为{1，2，…，j，…，D}，Fuch映射的表达式如下所示：

(21)

取Fuch混沌序列的初始值z(0)=0.47，种群的规模SN=30，空间维数D=80，将式(21)产生的混沌序列映射到求解空间后得到初始化种群，种群个体xi，j如下：

xi，j=xmin，j+|Xn+1|(xmax，j-xmin，j)，i=1，2，…，SN，j=1，2，…，D，

(22)

其中，Xn+1为混沌值，xmax，j和xmin，j为搜索空间的上界和下界。

2.3.2 基于正弦函数的边界收缩因子I

在基本的ALO算法中，为了搜索陷阱里可能存在的解，边界因子I随迭代次数的增加而呈现阶跃式增加，从而导致搜索的空间的收缩存在不连续性，易错过最优解。假设搜索空间的上界ub=100，下界lb=-100，设迭代次数为100，算法中ub和lb的变化趋势如图2所示。

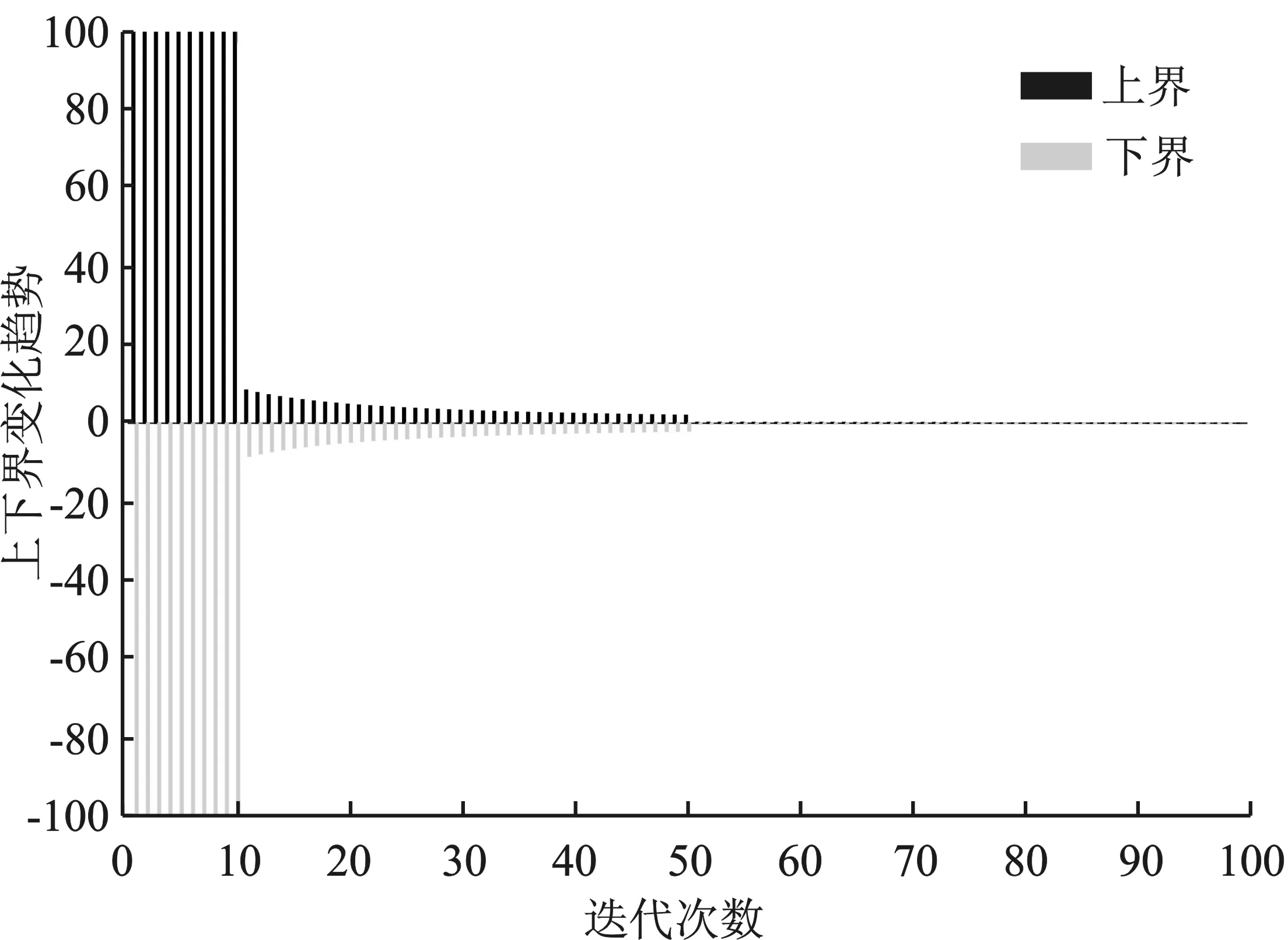
图2 原始算法的上下界变化趋势图

从图2可知，由于边界因子I由阶跃函数决定，陷阱的上下界呈现跳跃的状态，蚁狮捕捉蚂蚁过程中陷阱的收缩存在不连续性，导致算法易错过最优解，从而陷入局部最优。考虑到原始算法中陷阱收缩的不均匀性，将边界因子I替换为连续函数，即

I=αsin(0.5π(t/T))+β，

(23)

其中，t为当前迭代次数；T为最大迭代次数；α为系数；β为调节参数，经多次实验后取值为0.1。

将改进后的边界因子用于陷阱收缩中，假设搜索空间的上界ub=100，下界lb=-100，迭代次数为100，上下界的变化趋势如图3所示。

图3 算法改进后的上下界变化趋势图

从图3可知，由于改进后的边界因子I是连续性增加的函数，所以上下界的变化呈现出逐步递减的趋势，陷阱的收缩更加平滑，有利于种群搜索的遍历性，从而增强了算法的寻优能力。

2.3.3 时变策略

为进一步提升算法的探索能力，采用一种基于时变高斯变异的蚂蚁位置扰动策略，利用高斯变异算子对蚂蚁的位置进行扰动，即

aposition*=aposition[1+γG(0，1)] ，

(24)

(25)

其中，aposition*为更新后的蚂蚁的位置，aposition为原始的蚂蚁位置，G(0，1)为高斯变异算子，γ为时变参数，t为当前迭代次数，T为最大迭代次数。算法前期γ较大，变异尺度大，有利于算法跳出局部最优。在算法后期，由于算法基本已收敛至最优，故此时γ较小，只对蚂蚁位置进行细微的扰动。

得到新的蚂蚁位置以后，计算新位置所对应的适应度函数，再根据与原始蚂蚁位置的帕累托支配的关系决定是否更新解的位置。改进后的算法伪代码如下所示。

算法1IMOALO伪代码。

参数设置：最大迭代次数为T，当前迭代次数为t，蚂蚁数目为Numa，蚁狮数目为Numb，种群的维数为dim，初始外部存档中解的个数为N，存档中实际存在的解的个数为N1，变量上下界为ub和lb。

种群初始化：按式(21)和式(22)产生初始化种群，计算适应度值后存入Archive中，并按蚁狮间的支配关系选择出精英蚁狮。

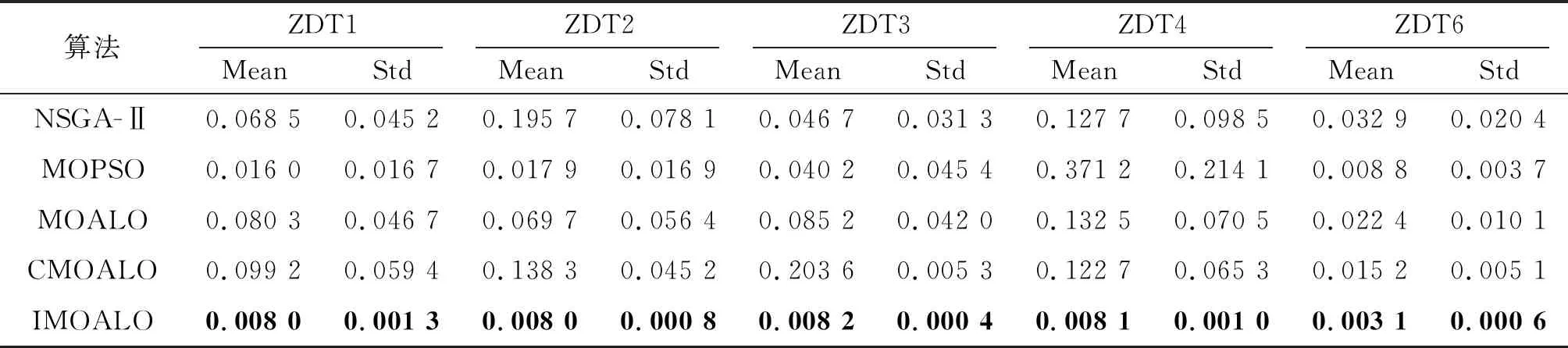
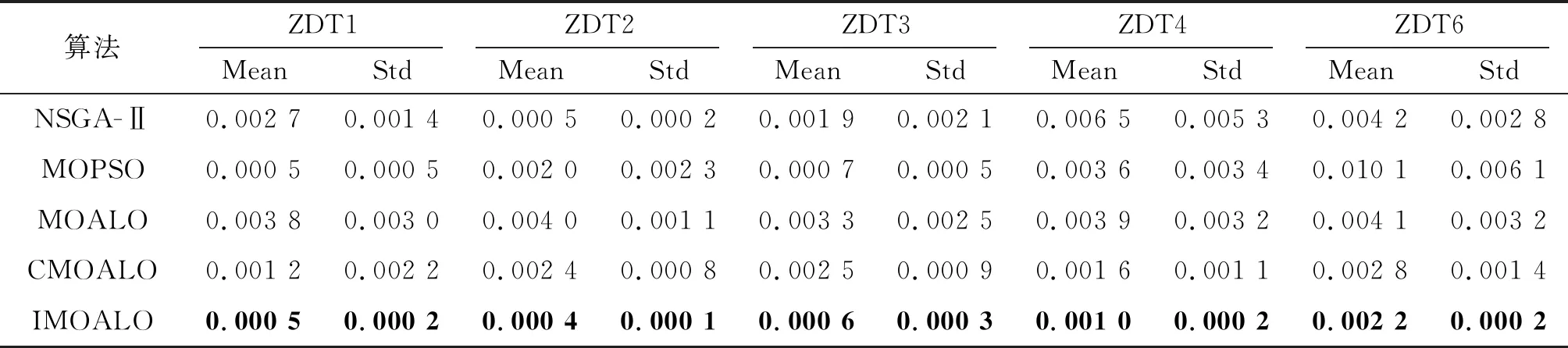
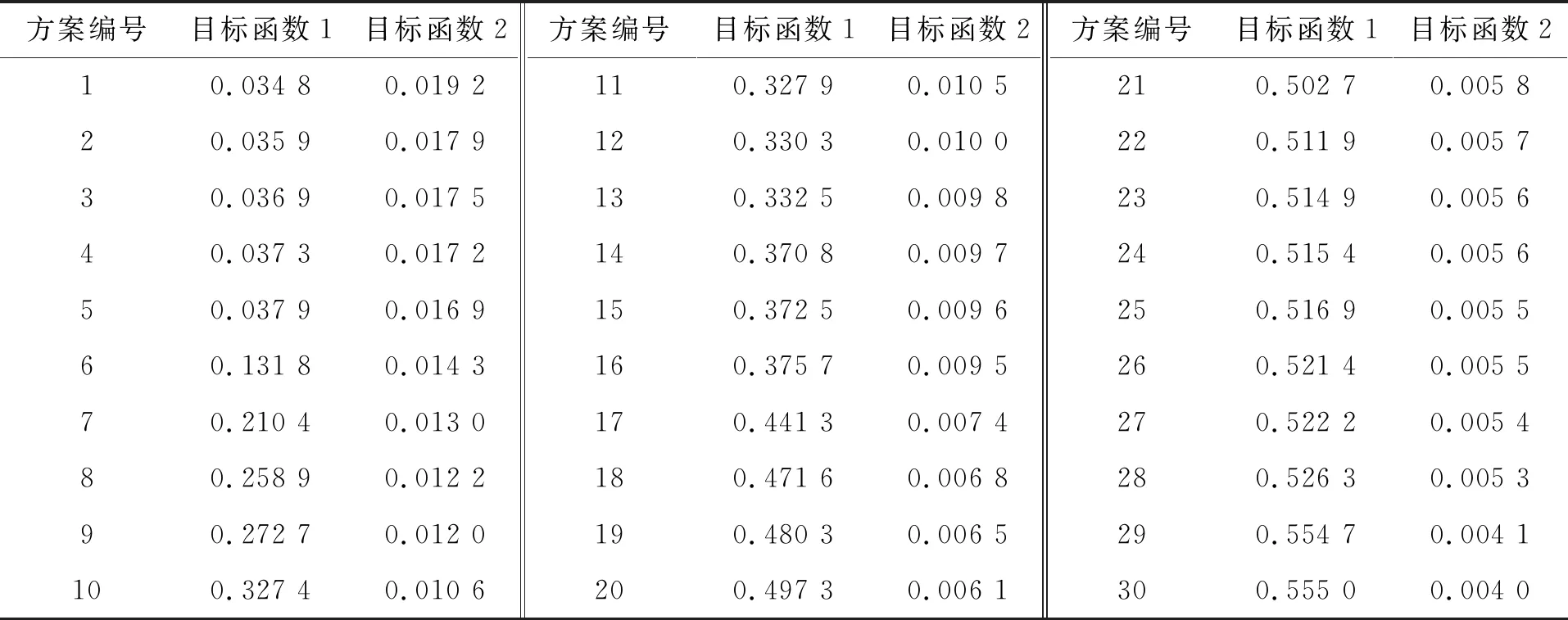
Whilet

For every ant

从Archive中随机选择一个蚁狮和精英蚁狮

按式(16)和式(23)更新c和d的值

蚂蚁按式(12)和式(14)进行随机游走

按式(18)更新蚂蚁的位置aposition，并计算其适应度Fa

由式(24)干扰蚂蚁的位置得到新位置aposition*，并计算其适应度Fa*

WhileFa*可支配Fa

aposition=aposition*；

End while

End for

根据支配关系更新Archive并按照拥挤度进行排序

选择排序在第1位的蚁狮为精英蚁狮

IfN1>N

则按式(20)和轮盘赌的方式删除多余解

End

End while 。

2.4 算法时间复杂度分析

设置目标函数的维数为m，种群个数为n，迭代次数为T，初始化种群的时间复杂度为O(2mn)，更新外部存档Archive的时间复杂度为O(n)。若外部存档Archive超出设定值，则需要对外部存档Archive进行删减，其时间复杂度为O(n2)；轮盘赌方式选择精英蚁狮的时间复杂度为O(n)，更新蚂蚁位置的时间复杂度为O(mn2)，蚂蚁位置扰动的时间复杂度为O(mn)，时变策略的时间复杂度为O(mn)，故IMOALO算法的时间复杂度为

O(m，n，T)=T(O(2mn)+O(n)+O(n2)+O(n)+O(mn2)+O(mn)+O(mn))=TO(mn2) 。

由文献[19]可知，MOALO算法的时间复杂度也为TO(mn2)。综上，笔者提出的策略没有增加算法的时间复杂度。

3 算法性能测试

为了检验改进后算法的有效性，利用多变量的双目标函数ZDT1、ZDT2、ZDT3、ZDT4、ZDT6对算法进行测试，并与多目标算法MOALO[19]、NSGA-Ⅱ[26]、MOPSO[27]、CMOALO[28]进行对比。本实验仿真环境为：Win10操作系统，AMD Ryzen5 2500U with Radeon Vega Mobile Gfx @2.00 GHz主频，8 GB内存，MATLAB 2016a。

3.1 评价指标

在帕累托解集中，解集应更贴近真实的前沿面，且还应具备一定的分布性，世代距离(Generational Distance，GD)可用于评价算法的收敛性，反向世代距离(Inverted Generational Distance，IGD)可用于评价算法的收敛性及解的分布性。GD值越小，表示求得的帕累托解集越接近真实的帕累托前沿面；IGD值越小，说明获得的帕累托前沿面的收敛性越好。

3.2 实验结果

实验中蚁狮的数量为30，蚂蚁的数量为30，最大迭代次数为100，外部存档Archive的大小为100，图4～8为算法在各个多目标算法在测试函数上的分布情况。从左到右分别为NSGA-Ⅱ、MOPSO、MOALO、CMOALO、IMOALO。图中，True PF为真实的帕累托前沿，Obtained PF为求解获得的帕累托前沿面。

图4 4种不同算法在ZDT1下的前沿面

图5 4种不同算法在ZDT2下的前沿面

图6 4种不同算法在ZDT3下的前沿面

图7 4种不同算法在ZDT4下的前沿面

图8 4种不同算法在ZDT6下的前沿面

由图4～8可知，IMOALO算法在求解ZDT6时只有一个解没有落在帕累托前沿面上，其余均落在真实的帕累托前沿面上，对比于其他几种经典的多目标算法，IMOALO算法的收敛性和分布性均优于其他多目标算法。这表明提出的策略有效地提升了多目标蚁狮算法的性能。

为更准确地评估IMOALO的性能，将上述算法在测试函数上运行30次，得到对应的GD和IGD值，实验结果如表1和表2所示，其中加粗的为每一列的最小值，Mean为均值，Std为标准差。

表1 4种不同算法下的IGD指标值

表2 4种不同算法下的GD指标值

由表1和表2可知，IMOALO与其他几种多目标算法相比，具有最小的IGD和GD值，算法收敛性和解的分布性均优于所对比的算法，且对应的标准差最小，表明改进后的算法稳定性更好，相比于其他两种多目标蚁狮算法都有较大的提升。

4 实验仿真及结果分析

4.1 实验参数设置

为了验证IMOALO算法解决部署问题的有效性以及相对于其他多目标优化算法的优越性，将节点部署在面积为100 m×100 m的监测区域内，节点个数为40个，节点的感知半径Rs为10 m，节点的通信半径Rc为16 m。使用MOPSO、MOALO、CMOALO以及无连续性收缩性边界的MOALO、IMOALO算法分别对1.4节中的模型进行求解，设置帕累托最优解集个数为30。

4.2 覆盖率与连通性的Pareto前沿面

为直接反映目标函数间的博弈性和求解算法的有效性，选择连通性和覆盖率两个目标函数进行试验，其中目标函数1为区域的未被覆盖率，目标函数2为节点之间的连接数目的倒数，结果如图9所示。

由图9可知，基于IMOALO算法下的解分布较为均匀，且获得的解的数量远多于其他几种算法，解的分布更广，且帕累托前沿面更靠近坐标轴，解的性能更优。将无连续性收缩边界的MOALO算法与IMOALO算法的解对比可知，在添加收缩边界以后，解的数量明显增加，有效提升了算法的探索能力。总的来说，IMOALO相对于其他几种算法有着更好的优化性能，能够有效解决节点部署中的多目标优化问题，也进一步验证了IMOALO算法的有效性。

图9 不同算法的Pareto解集

表3是IMOALO算法优化得到的帕累托解集对应的目标函数值，共对应了30种不同的策略，对区域的覆盖可达约96.52%，基本将整个区域覆盖，最小约为44.50%；节点连接的数目最多达到250个，最少为52个，其中每一个节点都至少能与一个其他节点连通。

表3 帕累托最优解集

图10～12是从帕累托解中选择出来的3种典型的节点部署方案：方案1侧重于整个区域的覆盖；方案2侧重于节点间的连通度，网络中冗余度较大，适用于具有重点区域部署需求的监测环境；方案3则是在覆盖率与连通度之间做一个折中。由此可见，基于IMOALO算法的节点部署策略能够有效处理多目标需求下的节点部署模型，并获取多个节点的部署方案，提供更广的决策空间。

(a) 节点覆盖效果图

(a) 节点覆盖效果图

4.3 不同节点数目下的Pareto前沿面

为分析节点数目对区域覆盖率与连通性的影响，以及不同节点数目下的解集分布，以便在节点数目发生变化时能进行快速决策，在相同的区域内分别部署20、25、30、35、40、45个节点。实验结果如图13所示。

图13 不同节点数目下的帕累托前沿面

由图13可知，当节点数目不同时，所提算法均能获得数量较多的解，且解的分布较广，随着节点数目的递增，帕累托前沿面呈现递增的趋势。但不同节点数目下的连通度和覆盖率可能存在相等的情况，不同节点数目下的解有重叠的解。从图中还可以看出，节点数目为40个与节点数目为45时节点的连通性度与覆盖率相差较小，在决策时可挑选节点数目小的一组解，减少节点的使用数量，降低部署的成本。

5 结束语

笔者提出了一种基于IMOALO算法的无线传感器网络节点部署策略。首先，分析了节点部署中各个目标间存在的冲突，构建了节点多目标部署函数；然后，针对原始MOALO算法寻优能力不强易陷入局部最优的缺点，通过混沌初始化和连续性边界收缩因子策略来提高算法搜索的遍历性，添加时变机制对蚂蚁位置进行扰动，以增强算法寻优能力。并与其他多目标算法在测试函数上进行测试对比，验证了IMOALO算法的有效性；最后，将IMOALO算法应用在节点多目标部署问题中，结合帕累托前沿面的思想平衡不同目标之间的矛盾。仿真结果表明，所提算法能有效解决节点多目标部署问题，可为决策者提供多个方案，具有较好的应用价值。