基于响应面法对注塑工艺参数的优化

李嘉成，张吴飞，李帅帅

（200000 上海市 上海理工大学）

0 引言

注塑成型是极其复杂的过程，在此过程中可能影响产品质量的工艺参数多且非线性变化[1]，工艺参数主要有：模具温度、熔体温度、注射压力、填充时间、保压压力、保压时间、冷却时间。衡量产品质量的指标也多种多样[2]。本文以翘曲变形量和体积收缩率为产品指标，为了兼顾各产品指标，按指标对产品质量的影响程度，先进行无量纲化处理，再采用模糊映射法按百分制对其进行加权，其中翘曲变形量占30%，体积收缩率占70%。通过Design-Expert 软件建立各工艺参数与产品指标间的关系[3]，以极差和方差比较筛选出对产品质量影响较大的工艺参数作为设计变量，以翘曲变形量和体积收缩率为响应变量[5-6]，拟合出回归响应面模型[7-8]，用方差和残差验证模型的可靠性[4]。利用多目标遗传算法[9]解出响应面模型的最优解，最后将解代入Moldflow 软件中进行验证。

1 Moldflow 注塑成型工艺试验设计

1.1 试验模型

该塑件是某医疗器械上的对合针槽，如图1 所示。产品注塑使用ABS 塑料。对合针槽的尺寸为30.00 mm×20.00 mm×30.00 mm。在Moldflow 软件中进行壁厚分析，产品的平均壁厚2.9 mm，最大为3.2 mm，最小为0.4 mm。

图1 Moldflow 试验模型Fig.1 Moldflow test model

1.2 注射工艺参数

在注塑成型过程中对注塑件产品质量有较大影响的工艺参数主要有模具温度（A）、熔体温度（B）、注射压力（C）、填充时间（D）、保压压力（E）、保压时间（F）、冷却时间（G）[2]。根据Moldflow 推荐的工艺参数范围及水平表见表1。

表1 试验因素及水平Tab.1 Test factors and levels

2 正交试验设计

Design-Expert 推荐的试验方法主要有Taguchi法、Central-Composite 法和Box-Behnken 法，本研究采用Taguchi 法。将Taguchi 试验设计表格数据[3]如表2 所示。

表2 Taguchi 试验设计结果Tab.2 Taguchi test design results

（续表）

2.1 极差分析

结合极差分析可研究各因素水平对响应变量影响[4]的权重R 值，R 值越大，影响程度越大，结果如表3 所示。

表3 翘曲变形量的极差结果分析Tab.3 Analysis of range results of warpage deformation

根据表3 中的极差数据，对于翘曲变形量[5]，各因素对其影响程度依次为熔体温度 >填充时间 >模具温度 >保压压力 >冷却时间 >保压时间 >注射压力。

据表4 中的极差数据，对于体积收缩率[6]，各因素对其影响程度依次为熔体温度 >填充时间 >保压压力 >保压时间 >注射压力 >模具温度 >冷却时间。

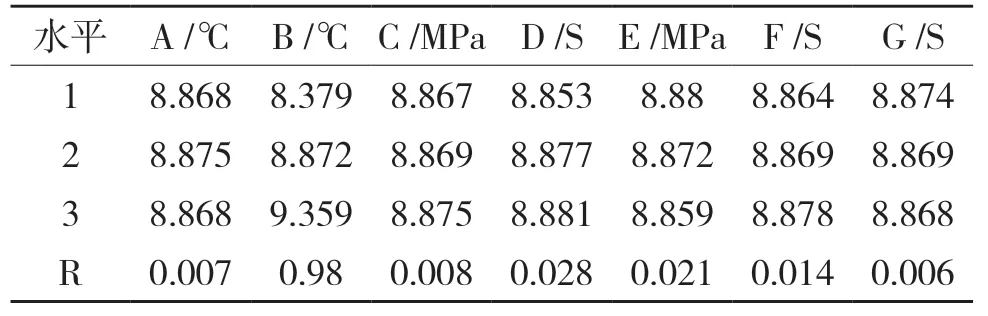
表4 体积收缩率的极差分析结果Tab.4 Range analysis results of volume shrinkage

由上可见，各个因素对不同产品指标的影响规律不同，需要通过综合评分实现产品质量多目标综合评判。权重分配根据各目标值对产品质量的影响程度，按百分制加权，将翘曲变形量和体积收缩率的权重定为w1=30%，w2=70%，百分制加权评判公式为：

式中：i——试验序号；Yi——第i 组试验综合评分。

由于翘曲变形量和体积收缩率的量纲不同，需要数据归一化处理，再将二者映射到[0，1]的数值空间中，按百分制进行加权处理。综合评分的极差分析结果见表5。

表5 综合评分的极差分析结果Tab.5 Range analysis results of comprehensive score

由表5 可知，各因素对产品质量的影响程度依次为：熔体温度（B）>填充时间（D）>保压压力（E）>保压时间（F）>注射压力（C）>模具温度（A）>冷却时间（G）。

2.2 方差分析

结合方差分析定量评估各因素对翘曲变形量和体积收缩率的影响程度，去除不显著项后的分析结果如表6、表7 所示。

表6 翘曲变形量的方差结果分析Tab.6 Variance analysis of warpage deformation

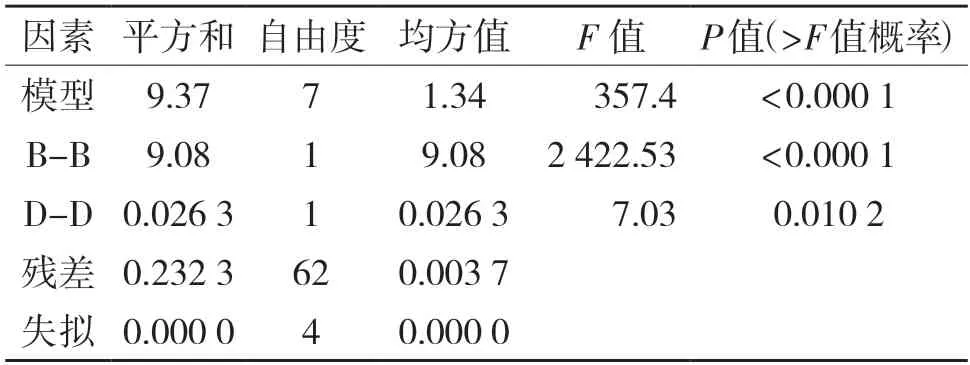
表7 体积收缩率的方差结果分析Tab.7 Variance analysis of volume shrinkage

3 响应面模型的建立与验证

结合上文，对总评分影响程度较大的试验变量有熔体温度、填充时间、保压压力，而保压时间、注射压力、模具温度和冷却时间对产品质量的影响程度较小。

根据上文结论，选择熔体温度、填充时间和保压压力作为设计变量并建立与响应变量之间的响应面模型，采用Design-Expert中的Box-Behnken法，其中模具温度、注射压力、保压时间、冷却时间分别取80℃、200 MPa、15 s、18 s。

本文以最小二乘法拟合响应面函数，并将其应用到产品响应变量上，利用Box-Behnken 试验采集的30 组设计变量与响应变量的试验数据构建响应面模型[7-8]，采用二次多项式作为构造函数。

3.1 翘曲变形量的响应面模型

根据Box-Behnken 试验设计结果，拟合关于体积收缩率的二次多项式响应面近似函数为：

在得出响应面模型后，有必要进行模型验证其精确性，选取方差和残差作为检验工具。

从表8 和图2 中可以看出，每个设计变量对翘曲变形量结果的影响非常显著，每个设计变量的残差基本拟合在一条直线上，表明翘曲变形量的响应面模型满足最小二乘法回归分析的要求。

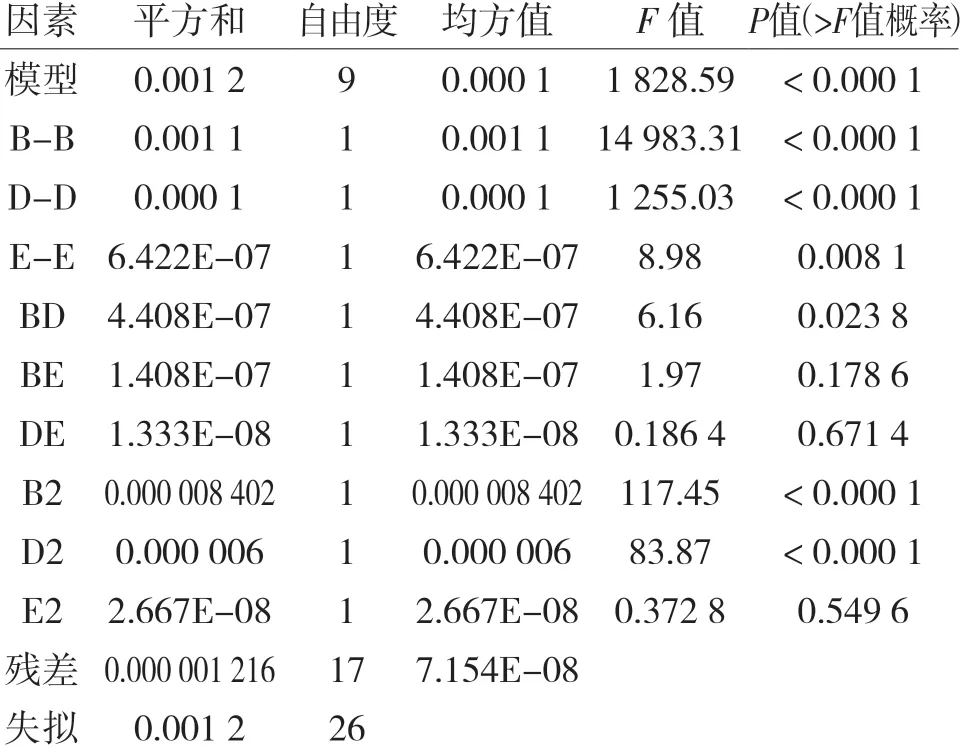
表8 翘曲变形量的方差结果Tab.8 Variance results of warpage deformation

图2 翘曲变形量残差Fig.2 Warpage deformation residual

3.2 体积收缩率的响应面模型

根据Box-Behnken 试验设计结果，拟合关于体积收缩率的二次多项式响应面近似函数为：

在得出响应面模型后，有必要进行模型验证其精确性，选取方差和残差作为检验工具。

从表9 和图3 中可以看出，每个设计变量对翘曲变形量结果的影响非常显著，每个设计变量的残差基本拟合在一条直线上，表明翘曲变形量的响应面模型满足最小二乘法回归分析的要求。

表9 体积收缩率的方差结果Tab.9 Variance results of volume shrinkage

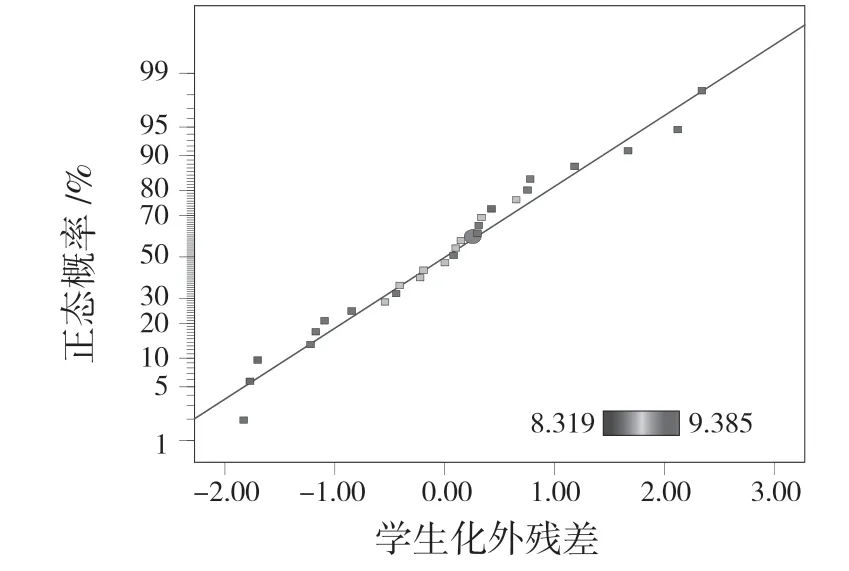
图3 翘曲变形量残差Fig.3 Warpage deformation residual

4 多目标遗传算法寻优

基于上文拟合好的响应面模型，利用MATLAB自带的遗传算法工具箱进行寻优[9]，变量个数为3，优化范围：熔体温度B 为220～240℃，填充时间D为0.2～0.6 s，保压压力E 为80～100 MPa。种群规模为200，迭代次数为100，交叉概率和编译概率分别为0.6 和0.08。

算法寻优结果：熔体温度为220 ℃、填充时间为0.2 s、保压压力为100 MPa 时，产品总评分为5.713，翘曲变形量为0.268 9mm，体积收缩率为8.321%，此时产品质量最优。

将算法寻优的结果代入Moldflow 中验证，得出翘曲变形量和体积收缩率分别为0.269 1 mm 和8.319%，将Moldflow 仿真结果和算法寻优结果对比验证[10]，可以看出响应面模型精确可靠。

5 结论

本文以壁厚不一的医疗器械为研究对象，针对其注塑工艺参数进行优化，发现当熔体温度为220 ℃、填充时间为0.2 s、保压压力为100 MPa 时，产品的质量最好，有效减少了产品的翘曲变形和体积收缩率，此时的翘曲变形量为0.268 9 mm，体积收缩率为8.321%。

使用响应面法和遗传算法对注塑模工艺参数优化起到了明显作用，在智能制造时代，建立数学模型指导实际塑料制件生产越来越普遍，算法的运用在其生产过程中发挥的作用也越来越大，基于响应面法对注塑工艺参数进行优化也是注塑模生产智能升级的一大助力。