孔喉结构薄膜热质传递的分形模型

张杰，张赛，高伟业，胡世旺，汪振毅

（650500 云南省 昆明市 昆明理工大学 机电工程学院）

0 引言

膜是一种典型的多孔介质，膜的传热传质特性是影响系统性能的关键因素，其传热传质特性已经成为工业领域的研究和应用热点[1-4]。苏铭[5]等认为膜的热质传递过程受气体和温度的影响，建立了气体通过膜介质的宏观传热传质模型。但孔隙微观结构对膜介质的传热传质也具有重要影响[6-7]；Zheng[8]等基于平行毛细管束模型，运用分形理论得出了气体扩散系数与多孔介质的面积分形维数、迂曲分形维数的关系。而实际上，孔隙之间往往相互交错，存在着多孔连通的情况；张赛[9]等考虑了孔的连通性，推导出了在孔道直径均匀不变情况下的气体扩散系数分形模型。实际孔道中，存在收缩孔道和扩张孔道（孔喉结构）两种情况[10]。王世芳[11]等、Wu[12]等考虑了孔道收缩和扩张的情况，假设孔道由正弦形弯曲毛细管组成，得到了多孔介质传热传质的分形模型，然而自然界中多孔介质孔道并不是精确的呈正弦形结构；郑坤灿[13]等基于孔喉模型，运用分形理论，推导了多孔介质的对流换热系数关联式，其关联式与传统对流换热准则方程较为一致，但是该模型是经过修正的。本文考虑了膜介质内部的微观结构以及膜介质内部孔道相互交错的情况，运用分形理论，推导出了气体通过膜介质的流速模型、扩散系数模型和换热系数模型，并且分析了多孔介质结构参数对气体流速的影响、流速对扩散系数和换热系数的影响。模型中的参数均有实际的物理意义，对膜介质传热传质过程的描述会更加准确。

1 膜介质孔特征参数

1.1 孔道分形特征

膜介质孔隙数目与孔隙大小满足式（1）[14]：

式中：N——孔道长度L 大于直径λ的孔隙数目；λmax——最大孔隙直径，m；Df——面积分形维数。Df由式（2）确定：

式中：dE——欧几里德维数。

式（2）表明，当孔隙率ε=1 时，dE=Df，即孔道空间是规则的。本文建立的相关模型都是二维平面上的，所以孔隙率满足式（3）[15]：

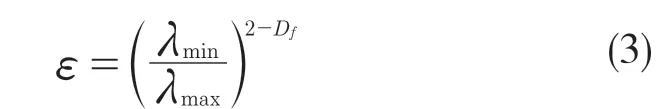
在λ到λ+dλ区间内对式（1）进行微分，得到此区间内的孔隙数目为

式（4）中，-dN（λ）>0。式（4）表明孔隙数目随孔隙直径的增大而减少。气体通过膜介质时，孔道是复杂且无序的，根据Yu 和Cheng[16]的分形模型，气体通过单根毛细管道的实际长度为

式中：L0——孔道的特征长度，m，本文模型中，孔道的特征长度即为膜介质的厚度；Dt——迂曲度分形维数，且Dt>1。

式中：Ap——孔隙总面积，m2，与膜介质面积分形维数、最大孔隙直径和孔隙率有关。

式中：At——横截面积，m2。

1.2 孔喉结构参数

气体在膜介质中流动时，其孔道空间由固体颗粒堆积而成。如图1 形成了大小不同的孔喉结构，孔喉结构连接在一起即为孔道空间。图2 为局部孔喉结构微观模型。在该模型中，LBF为喉道直径(m)，喉道是变化的，即LBF=λ，孔道直径为LBF+DP，DP为固体颗粒直径(m)，则最大孔径大小随喉道直径和固体颗粒直径变化的关系为

图1 颗粒堆积三维模型Fig.1 Three-dimensional model of particle accumulation

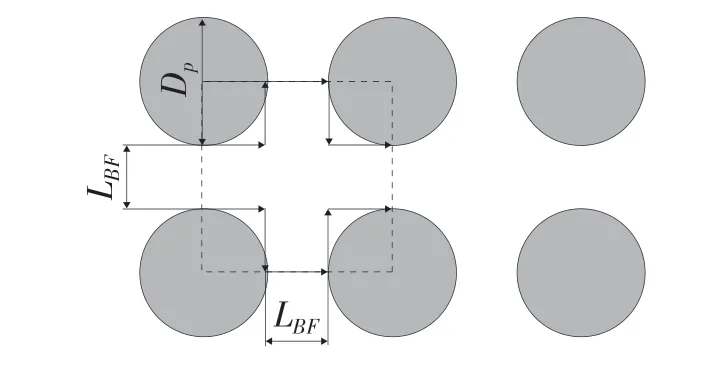
图2 孔喉结构二维模型Fig.2 Two-dimensional model of pore-throat structure

式（8）表明，孔道直径大小随固体颗粒直径和喉道直径的变化而变化。该模型的孔喉比为

如图2 所示，扩张孔道的孔隙面积为

由图2 可以看出，固体颗粒突出在孔道空间中，其占孔道空间的面积为

则气体流过单个孔喉模型的有效面积为：

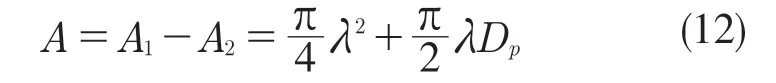
式（12）表明，气体在孔道中流动的面积与喉道直径和固体颗粒直径有关，固体颗粒直径一定时，其流动面积随喉道直径的增大而增大。

2 理论模型

2.1 气体流速的分形模型

气体通过膜介质时，由于孔道中存在孔喉结构，孔道的收缩和扩张会使气体存在局部动能损失[16]。文献[17]表明，气体通过孔喉结构时产生的压力梯度为

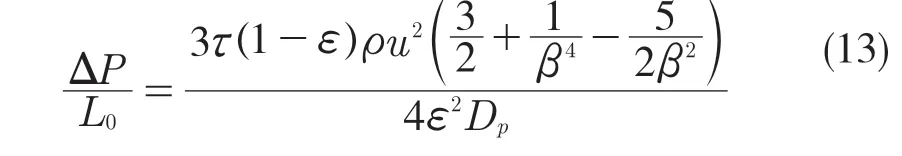
式中：ΔP——压强差，Pa；u——气体流速，m/s；ρ——气体密度，kg/m3；τ——孔道迂曲度。

由式（13）可得，孔喉结构处的压强差为

联合式（4）、式（5）和式（14）得：

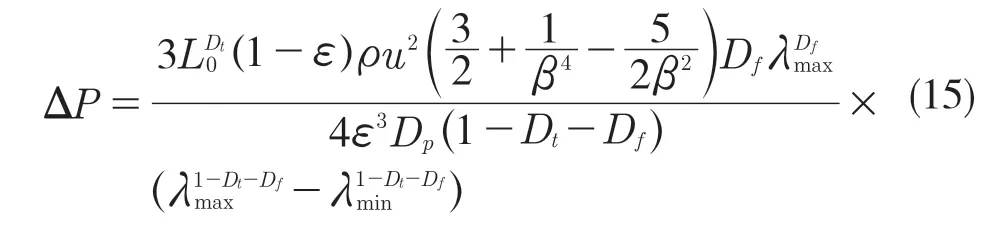
式（15）表示了由于孔喉结构、孔隙率、面积分形维数、迂曲分形维数和孔隙大小等引起的压强损失。分析式（15）可发现，当孔隙率减小时，压强差增大，这与实际情况是一致的。由式（15）可得气体通过膜介质的流速模型为

式（16）是基于分形理论和孔喉结构模型求出的流速模型，此模型中每一个参数都有其明确的物理意义。式（16）表明，气体流速与孔喉比、压强、孔隙率、密度、孔的迂曲分形维数、孔的面积分形维数、孔的大小和膜介质的厚度等有关，能真实地描述膜介质中孔喉结构作用下气体的流动机理。上述流速模型包含了2 类参数，一类为膜介质孔结构参数，另一类为气体参数。

2.2 气体扩散的分形模型

前面的分析已经指出，孔道空间存在压强差，压强的存在促使气体在孔道空间流动。当气体具有一定的流速u 时，单个孔道空间的流量为

联合式（4）和式（12），气体流过膜介质的总流量为

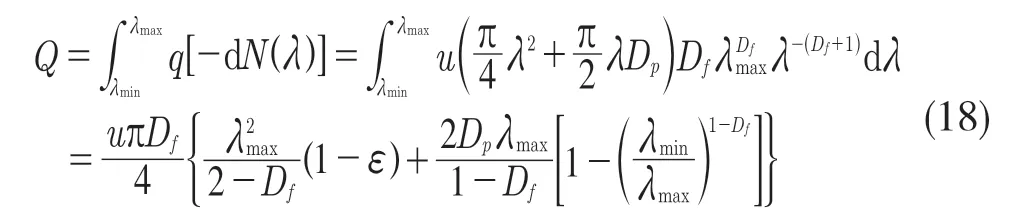
式（18）表明气体流量随流速的增大而增大。膜介质的质量传递过程中，气体通过膜的驱动力主要为膜两侧的浓度梯度，根据Fick 第二定律，通过膜介质的气体流量为

式中：Dk——气体扩散系数，m/s2；ΔC——膜介质两端的浓度差，mol/L，且ΔC=ΔP/RT，其中，R——气体常数（8.314 J/(mol·K)），T——温度，℃。联合式（7）、式（18）和式（19）可得：

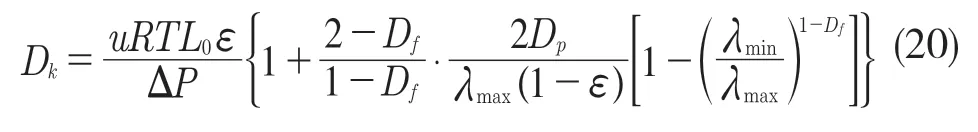
式（20）表明，扩散系数Dk与孔隙率、流速、压强、温度、面积分形维数、粒子直径、最小孔径、最大孔径等有关。显然，此模型真实地描述了气体在膜介质中的扩散机理。

2.3 气体换热的分形模型

根据能量守恒定律，气体流过膜介质时热量的变化量等于气体与膜介质内壁的换热量：

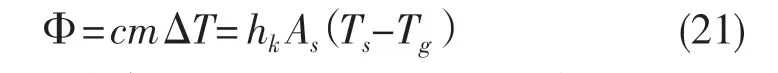
式中：c——比热容，J/(kg·℃)；m——质量流量，kg/s；hk——换热系数，W/(m·2K)；As——膜介质孔道内表面积；Ts——固体温度；Tg——气体温度；ΔT——膜介质两端的温度差。

式（21）表明换热主要由膜介质内部温度差引起。

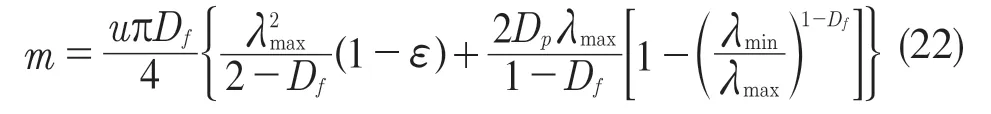
联合式（21）和式（22）求得：

式（23）表明换热系数与气体的密度、比热容、孔道内表面积、温度和气体流量有关。将式（23）转换为努赛尔形式：

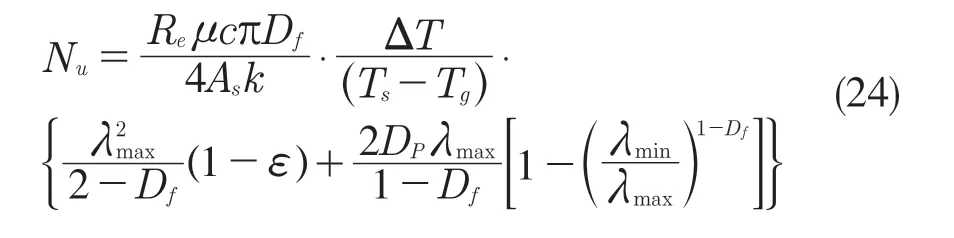
式中：μ——气体粘度，Pa·s；k——气体导热系数，W/(m·K)；Nu——努赛尔数。努赛尔数与换热系数为线性关系，即努赛尔数的变化充分体现了膜介质换热系数的变化。Re——雷诺数，定义为Re=ρDpu/μ，雷诺数与粒子直径、气体流速、密度和粘度有关。

3 分析和讨论

以上扩散系数与换热系数都包含了气体流速，研究膜介质的传热传质问题，气体流速是不可忽略的重要因素。

图3 为膜介质扩散系数模型与文献[18]实验数据的对比图。由图3 可见，扩散系数理论模型与实验数据吻合度较高。该模型是根据气流速度推导得到的，本文根据Ding 的实验数据[29]，计算得到气流速度并取u=1.5 m/s，此外λmin/λmax≈0.001。由图3 可知，随着孔隙率的增加，气体扩散系数增大，这是因为孔隙率增大，孔道空间变大，气体流通性好，而气流本身具有一定的速度，流通性好则流过孔道的流量增加，所以扩散系数增大。

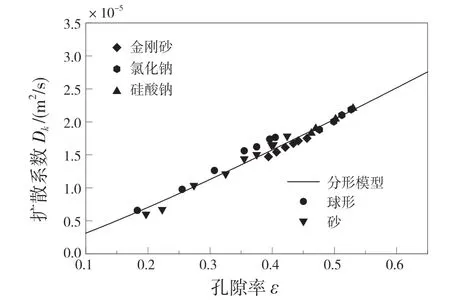
图3 扩散系数模型预测值与实验数据对比Fig.3 Comparison between predicted values of diffusion coefficient model and experimental data

图4 为式（24）与文献[20]实验数据的对比图，粒子直径分别取1×10-5m 和2×10-5m。由图4 可以看出，换热系数的分形解与实验数据吻合度较高。随着雷诺数的增加，膜介质的换热系数增加，雷诺数增大的原因在于气体流速增大。可以推断，当膜介质固体颗粒直径大小一定时，减小孔喉比，可以提高膜介质内气体的换热能力。

图4 换热系数分形解与实验数据对比图Fig.4 Comparison between fractal solution of heat transfer coefficient and experimental data

图5 表示孔喉比对气体流速的影响。由图5 可知，随着孔喉比的增大，气体流速大小变化显著，具体表现为固体颗粒直径大小一定时，孔喉比增大，流速下降，而增大到一定程度时，流速下降趋势变缓。这是因为孔喉比增大，喉道直径变小，并且当孔喉比增大到一定程度时，意味着孔道空间几乎被固相占据，所以气体通过膜介质的阻力变大。由图5 还可以看出，当固体粒子直径增大时，气体通过膜介质的速度也在变快，这是因为粒子直径增大时，结合式（8）分析，孔道直径在增大，气体阻力变小，所以流速变快。

图5 粒子直径对气体流速的影响Fig.5 Influence of particle diameter on gas velocity

图6 为迂曲度分形维数分别取1.3，1.4，1.5 时，流速随孔隙率的变化关系图。由图6 可知，随着迂曲度分形维数的增大，气体流速变慢，这是因为迂曲度分形维数越大，表示毛细管道越弯曲，气体通过膜介质的路径变长，且通过膜介质时受到的阻力大，气体的流动能力变差，所以流速变慢。

图6 迂曲度分形维数对气体流速的影响Fig.6 Influence of fractal dimension of tortuosity on gas flow rate

图7 为不同面积分形维数情况下气体流速与孔隙率的关系图。由图7 可知，孔隙率一定时，气体流速随着面积分形维数的增加而减小，这是因为气体流量一定时，面积分形维数增大，孔道半径越均匀，气体受到的压强差减小，所以流速变慢。

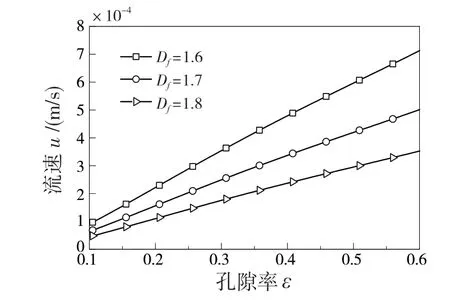
图7 面积分形维数对气体流速的影响Fig.7 Influence of surface integral dimension on gas velocity

图8 和图9 显示流速对扩散系数和换热系数有重要影响。在同一孔隙率情况下，流速变快时，气体流量增加，所以扩散系数增大，而气体携带了一定的温度，当气体流量增加，则有更多的气流参与到换热过程中，从而使换热系数也增大。

图8 流速对扩系数的影响Fig.8 Influence of flow rate on expansion coefficient

图9 流速对换热系数的影响Fig.9 Influence of flow rate on heat transfer coefficient

图10 为扩散系数随迂曲度分形维数变化的关系曲线图。由图10 可知，迂曲度分形维数减小时，扩散系数随着孔隙率的增大而增大，因为孔隙率增大时，孔道空间占比增大。由式（16）可知，气流速度与孔隙率呈指数关系，当迂曲度分形维数减小时，孔道实际长度相应地减小，迂曲度分形维数减小，由图6可知，气体流速变快，所以扩散系数增大。

图10 迂曲度分形维数对扩散系数的影响Fig.10 Influence of fractal dimension of tortuosity on diffusion coefficient

图11 表示面积分形维数分别为1.6，1.7，1.8时，扩散系数与孔隙率的变化关系图。由图11 可知，扩散系数随着面积分形维数的增大而增大，这是因为Df增大，意味着孔隙数目增加，气体扩散自由路径增加，扩散变得容易。

图11 面积分形维数对扩散系数的影响Fig.11 Influence of surface integral dimension on diffusion coefficient

图12 为迂曲度分形维数对换热系数的影响关系图。由图12 可知，迂曲度分形维数越大，换热系数越小，因为Dt增大，通过膜介质的气体流量减小。由式（21）可知，气体流量减小，则气体换热系数也减小。

图12 迂曲度分形维数对换热系数的影响Fig.12 Influence of fractal dimension of tortuosity on heat transfer coefficient

图13 为面积分形维数对换热系数的影响图。由图13 可知，随着Df的增大，孔隙率对换热系数的影响越来越显著。相对于较小的Df与ε，Df与ε增大表示孔道变得均匀且孔隙面积增大，气体扩散变得容易，气体流量增大，所以换热系数越大。

图13 面积分形维数对换热系数的影响Fig.13 Influence of surface integral dimension on heat transfer coefficient

4 结论

通过对膜介质中孔喉结构模型的理论推导和分析，得出如下结论：

（1）孔隙内部结构是影响气体流速的重要因素。气体流速随固体颗粒直径、孔隙率的增大而增大，随孔喉比、面积分形维数、迂曲分形维数的增大而减小。孔隙内部结构通过影响气体流速来影响膜介质的传热传质特性。流速变快，则通过膜介质的流量增大，扩散系数和换热系数增大。

（2）对比分析扩散系数与Currie 的气体扩散实验数据发现，扩散系数与孔隙率0.1～0.6 的不同多孔介质实验数据具有较高的一致性，说明此模型适用范围较广。

（3）换热系数的分形解与实验数据吻合度较高，分形解是基于孔道结构和分形理论求得的，更接近于气体在孔道内部的流动机理，显然，分形解模型可以指导膜介质孔道热量传递更深入的研究。