基于Bezier曲线的非轴对称端壁流动控制模拟与实验研究

朱培模，周 霖，付海晏，蔡 乐，王松涛

(1.中国航发贵阳发动机设计研究所，贵州 贵阳 550081；2.哈尔滨工业大学 能源科学与工程学院，黑龙江 哈尔滨 150001)

0 引言

叶片型面造成的损失和叶片上下端壁造成的损失在叶栅能量损失中占据着较为重要的地位。需要注意的是叶栅端部，在这个位置气流发展过程中会有气流横向运动的现象，将这种现象称为二次流。二次流的发展会引发一系列漩涡结构，其所引发的损失就是二次流损失。二次流损失是非常影响涡轮做功效率的，因此有必要研究降低二次流损失的方法手段。一般认为端壁二次流损失将占总损失的30%～50%。刘昊等人[1]指出燃气轮机叶栅端部二次流损失的影响因素，负荷与叶片端壁的面积比值大小会影响二次流损失的大小。对于高压涡轮，研究发现展弦比小的，它的二次流损失很大，达到总损失60%～70%。在研究端壁射流对端区二次流的控制作用和机理时，陈永强等人[2]认为二次流主要在叶栅端部形成发展，涡轮损失的一部分原因就来自在此位置发展的端区二次流和泄漏流。另外，Booth在对单级涡轮进行研究时，发现端区损失很大，达到总损失的57%。为了造出来性能更好的航空发动机，势必带来大的透平涡轮叶片负荷，从而带来相当高的流动损失[3]。围绕流动损失的研究成果产生了多种减少流动损失的控制方法。其中1994年Rose[4]提出了非轴对称端壁的概念，通过将原型端壁改造为不对称的端壁结构，以实现影响端壁二次流发展的目的追求，从而探求控制二次流的方法手段。总的来说为了实现小的流道内部压力分布，就是通过端壁改变型线曲率来影响。无数的数值模拟和实验研究[5-13]，其中有很多成果可以说明，非轴对称端壁确实是影响涡轮机械二次流动的有效手段。到了现在，科学技术的发展涌现出了多种二次流流动控制技术，而非轴对称端壁造型技术一直是其中一种较为有效的控制技术。所以说想要发展高水平的燃气涡轮，其完全可以成为一种重要的技术手段来支撑涡轮的研究发展。也就是说结合叶栅实验方法和CFD数值模拟，进行非轴造型技术研究，探索非轴造型技术如何实现对涡轮内部流场的改变和生成发展的规律机理是很有必要的。可以看到是非常有利于涡轮的设计，其重要意义不言而喻。

1 造型方法介绍

Bezier曲线因其良好的性质在各行业得到普遍的运用，其控制点的数量决定着它的多边形的性质，进一步Bezier曲线的实际样式由这个多边形决定。Bezier曲线的计算公式为

(1)

式中Pi——下角标表示Bezier曲线第i个控制点；

Bi,n(t)——n次Bernstein多项式。

以数学形式表述为

(2)

由它的数学描述，可以看到根据给定n+1个控制点就能构造出相应的n次Bezier曲线。由原扇形叶栅损失构成分析，在上端壁进行构造。

具体使用Bezier曲线方法如图1(a)、图1(b)所示，8个控制点(Pi,i=0,1,…,7)，在流向控制线上分布。同时为了确保叶片前尾缘能够和构造的非轴端壁面无缝连接，曲线P0P1和曲线P6P7要与上端壁面前后方向吻合。要求8个控制点中，除了P2到P5能够沿径向移动，其余点不可妄动。这四个控制点径向移动的距离就是对应位置端壁曲面上下凹凸的距离。最终不同的流向控制线在周向排布以及流向位置通过Bezier曲线连起来，就能够形成完整的非轴对称端壁无量纲控制面。最后根据定义的非轴对称造型区域将无量纲控制曲面映射其上，完整的非轴对称造型端壁就构造完成了。

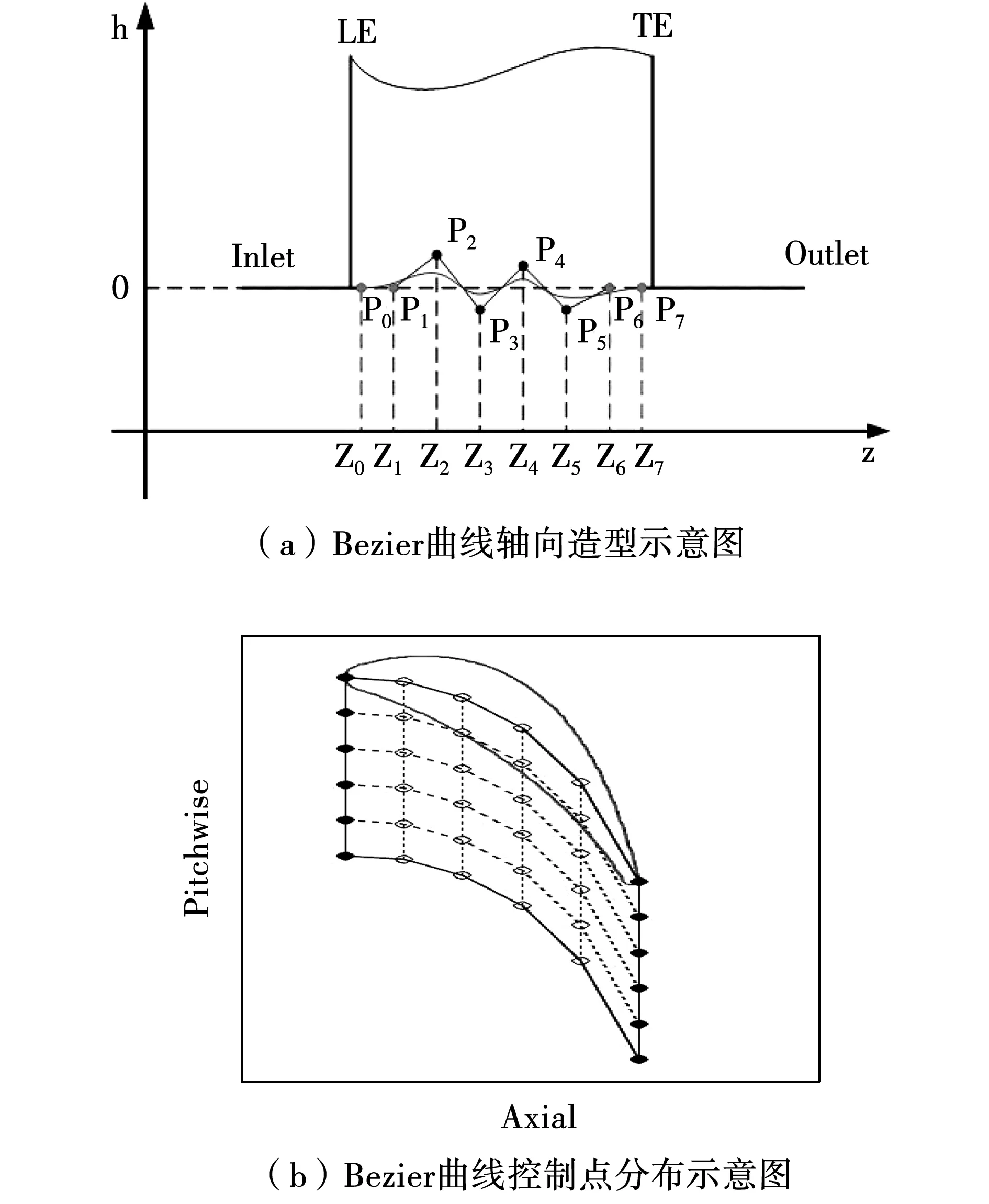
图1 Bezier曲线示意图

2 数值验证

需要通过引入湍流模型，使N-S方程组封闭从而求解。各个湍流模型有不同的适用计算精度。因此数值模拟验证的首要工作就是选择合适的湍流模型以确保数值模拟的精度。图2为验证计算使用的计算网格，y+值最大在数值8以内。使用AutoGrid5模块进行网格划分。

图2 计算网格示意图

具体的过程在CFD软件CFX进行，通过CFX-solve模块完成计算，计算之前要给定相应物性参数，入口总温和总的压力，还有气流角，出口物性参数设置平均静压，没提及壁面设定光滑无滑移。Ma=0.9，下同。图3为使用的各种湍流模型计算结果和实验结果基于叶栅出口处的能量损失系数沿叶高的分布情况，为了更好贴合实验数据以说明数值模拟的可信度，本文选了五种不同湍流模型来对比分析：BSL、EVTE(Eddy Viscosity Transport Equation)和k-Omega、SSG(SSG Reynolds Stress)以及SST(Shear Stress Transport)一共五种湍流模型来与实验进行验证。由图可以看到BSL和k-Omega在下端壁往主流上来与实验拟合较好，在上端壁位置略有不同；EVTE在上端壁位置偏差比BSL和k-Omega要大，其他位置拟合较好；SSG在上端壁拟合相差的都比较大，下端壁和主流位置还好；SST与其他几个相比主流位置拟合相差较大，上下端壁处比SSG和EVTE稍好，比BSL和k-Omega要差。通过分析可以发现除了SST模型在主流预测上偏差较大外，其余模型预测有偏差但较小，BSL和k-Omega模型是其中预测的比较好的湍流模型。在接近上端壁流场流动的预测情况也是如此，SST模型在对原扇形叶栅的预测中表现较差。

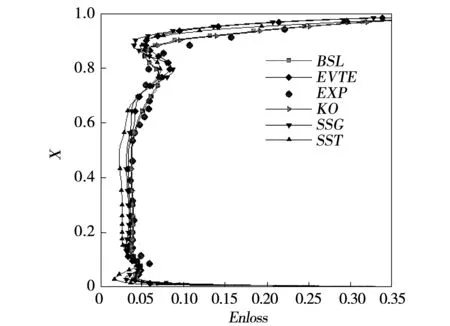
图3 湍流模型能量损失叶高分布与实验对比

图4为使用的各种湍流模型计算结果和实验结果基于叶栅出口处的总压损失系数沿叶高的分布情况，BSL和k-Omega从下端壁处开始往主流方向与实验对比良好趋势符合，在上端壁位置要略微大于实验数值；EVTE从下端壁一直到60%叶高处与实验比对良好，从60%叶高往上与实验结果对比较差，在上端壁处趋势与实验结果趋势符合，但与BSL和k-Omega相比则稍差,比实验值更大。SSG在下端壁处到22%叶高处与实验结果对比有较大偏差，从22%叶高到82%处与EVTE趋势相同，但略比EVTE要小部分位置略大于EVTE，与实验相差更大，接近上端壁处偏差更大是这几个湍流模型中拟合效果最差的。SST从下端壁往上70%叶高都是这几个湍流模型中与实验偏差最大的，是在主流位置就拟合相差的湍流模型，且偏小，70%到80%叶高处反而是最接近实验值的，80%叶高往上拟合部分略比SSG以及EVTE要好但差于BSL和k-Omega。

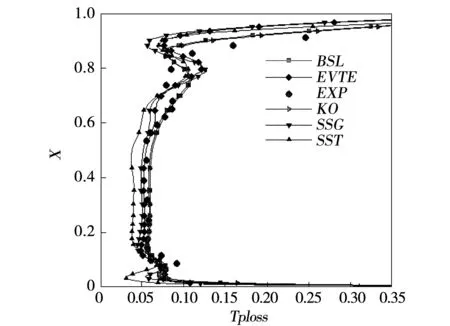
图4 湍流模型总压损失叶高分布与实验对比

通过以上实验结果和应用几种湍流模型的数值模拟计算结果基于能量损失系数以及压力损失系数沿叶高方向的分布比较来看，无论能量损失系数或者是压力损失系数对比，这几种湍流模型在接近上端壁处拟合的都存在偏差，其中BSL和k-Omega湍流模型拟合的最好与实验结果偏差最小，主流位置处BSL和k-Omega以及EVTE拟合实验结果都挺好，其它湍流模型较差，其中SST最差。结合以上分析为了确保数值模拟计算结果的可信度，通过几种湍流模型的拟合效果来看BSL和k-Omega湍流模型更加符合要求，所以本文后续均采用k-Omega湍流模型完成相关数值计算。

3 结果分析

3.1 端壁造型结果与验证

原扇形叶栅(Sector Cascade)以SEC来指明，非轴对称端壁(Non-Axisymmetric Endwall)以NON来表示。图5、图6是叶栅上端壁非轴造型图和原型叶栅、非轴造型上端壁半径对比图。

图5 NON上端壁造型示意图

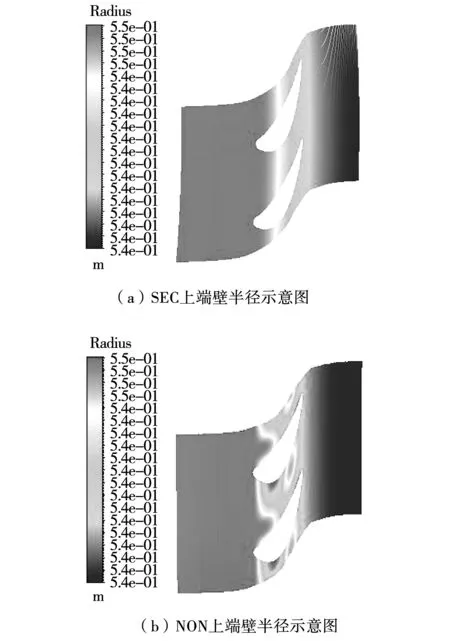
图6 上端壁半径示意图

图7、图8是数值模拟和实验结果在出口位置能量损失和总压损失沿叶高的对比图。图中实验和数值对应的气动工况为：来流为零攻角轴向进气，出口等熵马赫数为0.9，后续所有的分析均是针对此工况开展。由图可以看到数值模拟对实验的预测从下端壁往上一直到55%叶高处较为吻合能够较为真实反映实验流场，55%叶高往上到上端壁处与实验结果存在偏差。55%到约73%叶高处数值模预测略比实验值大，73%叶高到上端壁预测比实验值要小，说明数值模拟对上端壁附面层、涡系强度等预测的略有偏差，但总体预测良好。

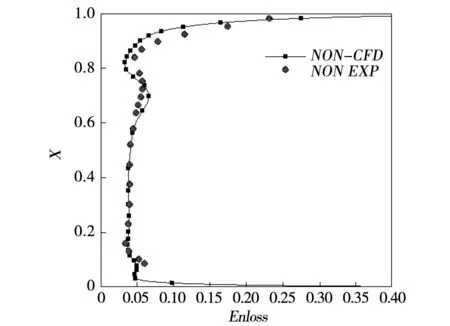
图7 非轴端壁能量损失叶高展示与实验对比

3.2 流动特性对比分析

将针对造型方法和原型端壁分析叶栅通道中流动损失的影响，以期探索非轴对称端壁造型如何改变二次流损失的原理。从下端壁到上端壁，沿叶高方向分别取10%，50%以及90%叶高处。图9到图11分别为相应型面静压分布示意图。由图可以看到从50%轴向一直到接近尾缘是两面之间压差最大的区域，代表着压力面与吸力面之间压力梯度最强，迫使附面层由压力面向吸力面迁移，这个区域的涡系有着较强的漩涡强度。由图9可以发现，由于是上端壁型面改造，故而对下端壁处10%叶高处静压力分布影响不大，原扇形叶栅与非轴对称端壁在10%叶高处静压力分布基本重合。

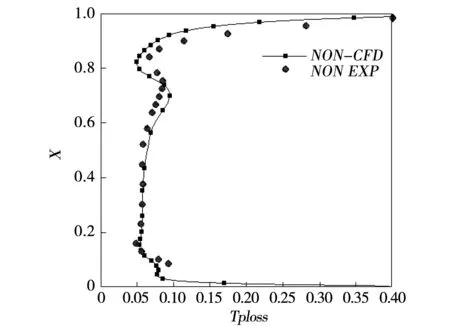
图8 非轴端壁总压损失叶高展示与实验对比

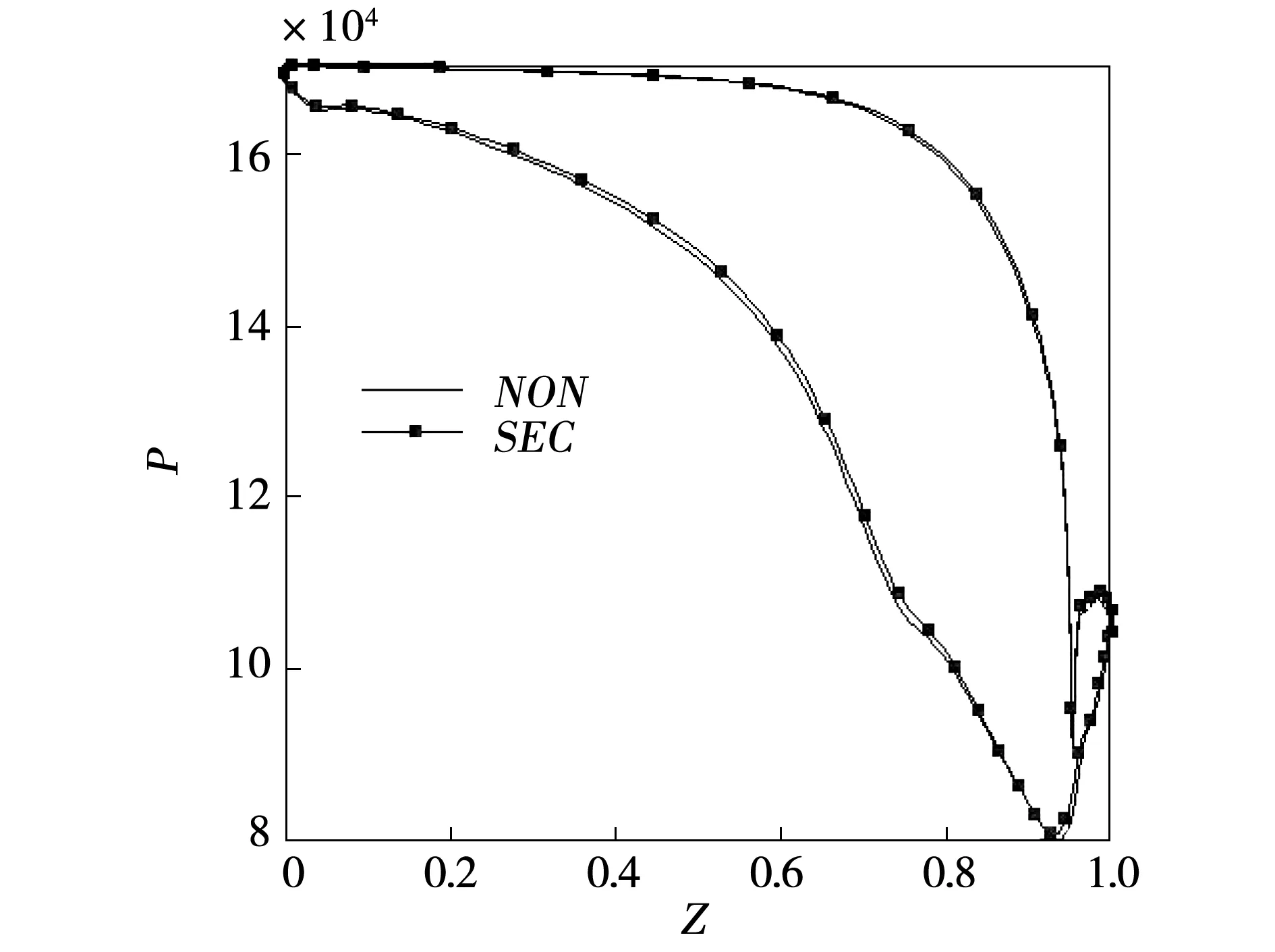
图9 10%叶高处型面静压分布

由图10可以发现，从开始一直到大约70%轴向处原扇形叶栅吸力面静压力比非轴对称端壁吸力面静压力要小，其它位置大体相同，部分略有差别，说明从50%叶高处非轴对称端壁造型对静压分布虽有影响，但不是很大。

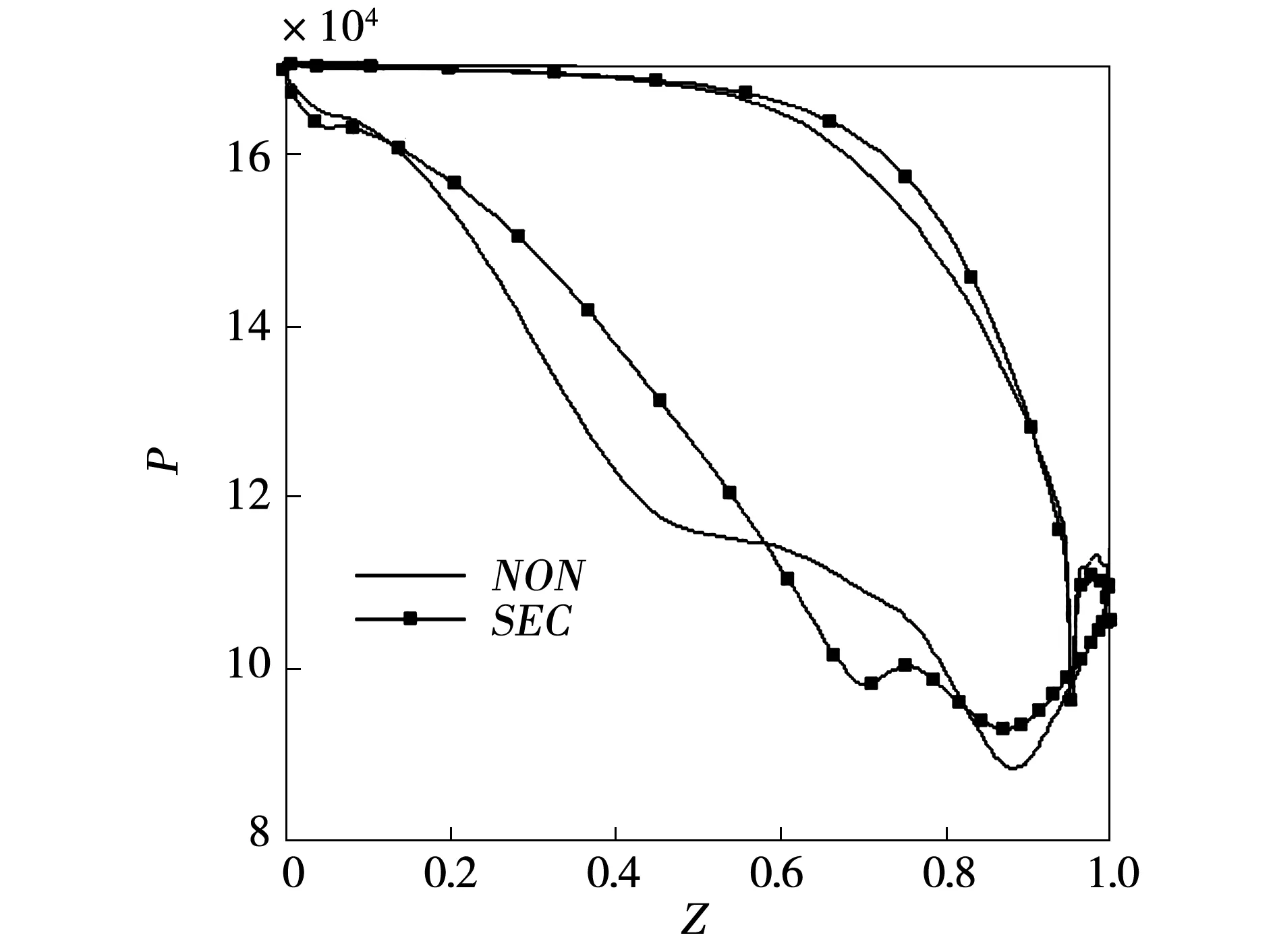
图10 50%叶高处型面静压分布

由图11可以发现从轴向约15%处一直到轴向58%处原扇形叶栅吸力面静压力比非轴对称端壁吸力面静压力明显要小，而在这个位置范围内原扇形叶栅压力面静压力和非轴对称端壁压力面静压力基本吻合，这说明在轴向约15%处一直到轴向58%处横向压力梯度非轴对称端壁比原扇形叶栅端壁横向压力梯度更大。需要注意的是轴向58%处到轴向约82%处这个压力梯度的差距反过来了，非轴对称端壁比原扇形叶栅端壁横向压力梯度变得更小，在这个位置范围对二次流损失的影响变得更小；轴向82%处到轴向93%处非轴对称端壁比原扇形叶栅端壁横向压力梯度也有一个较为明显的变化轴向，93%处到尾缘非轴对称端壁比原扇形叶栅端壁横向压力梯度要略差，但差距不是很明显。

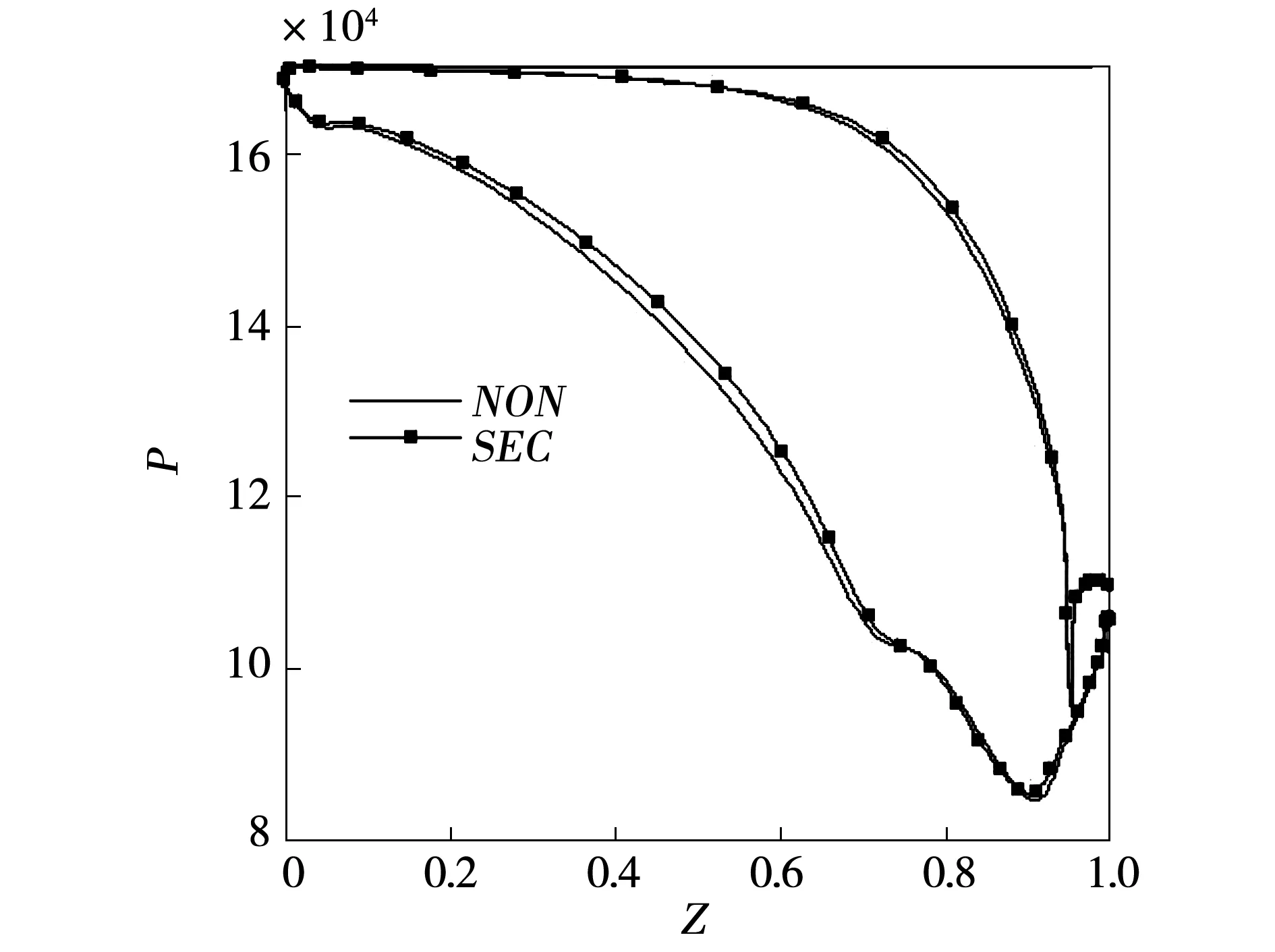
图11 90%叶高处型面静压分布

图12为90%叶高处型面等熵马赫数分布示意图。结合所学空气动力学知识以及图11和图12分析，原扇形叶栅在大约70%轴向区域之所以出现压力增加是因为随着流体从流道前缘流向流道尾缘的过程中速度越来越大马赫数约来越高达到跨音速流动产生激波，流体速度下降压力上升。而非轴造型是平滑变化，说明非轴造型在一定程度能够改善激波结构的产生。

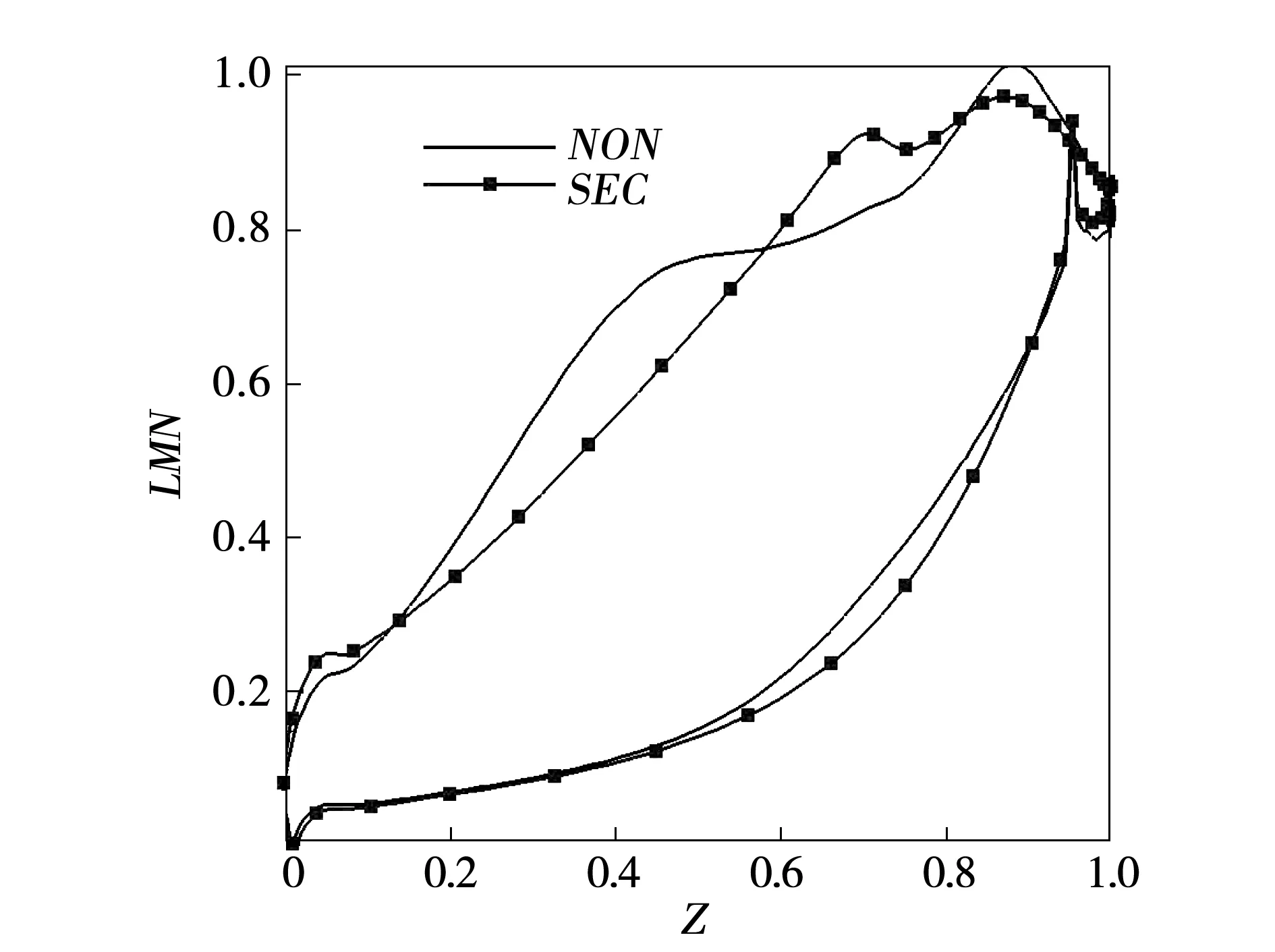
图12 90%叶高处等熵马赫数分布

图13是原扇形叶栅和非轴端壁叶栅上端壁的流线图，通过两图对比发现由于非轴造型上端壁凹凸结构使得非轴造型叶栅上端壁流场对比原扇形叶栅上端壁流场发生改变，非轴造型上端壁处马蹄涡较原扇形叶栅上端壁处提前分成两个分支。压力面涡系在凹凸壁面和压差的影响下提前和吸力面涡系交融。由两图对比发现在叶栅前半部分区域非轴端壁叶栅流道内的流线提前抵达吸力面。同时在吸力面会形成小范围的低压区域。

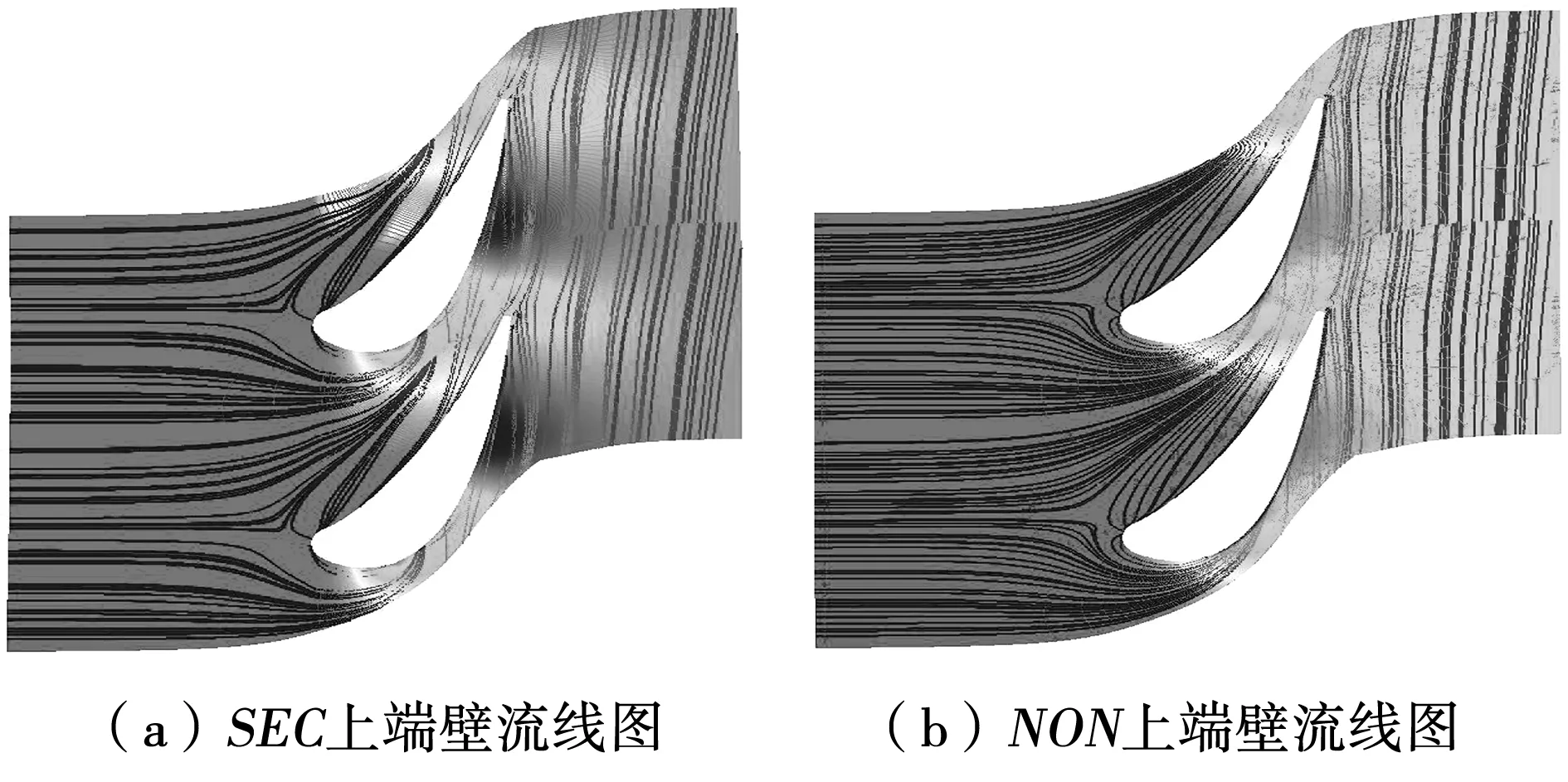
图13 上端壁流线图

3.3 非轴造型涡系分析

图14为非轴造型和原扇形叶栅上端壁漩涡结构对比显示图。由图可以清晰的看到非轴叶栅前半部分处的涡系结构与原扇形叶栅处相比漩涡结构发生了破碎，结合上文型面压力分布和上端壁流线图可知，由于压力的作用叶栅前半部分附面层很快完成迁移，虽然非轴造型压力梯度有所增加但影响较小，同时非轴凹凸的造型对涡系结构发展壮大起到了阻碍的作用，降低了涡系结构造成的损失。

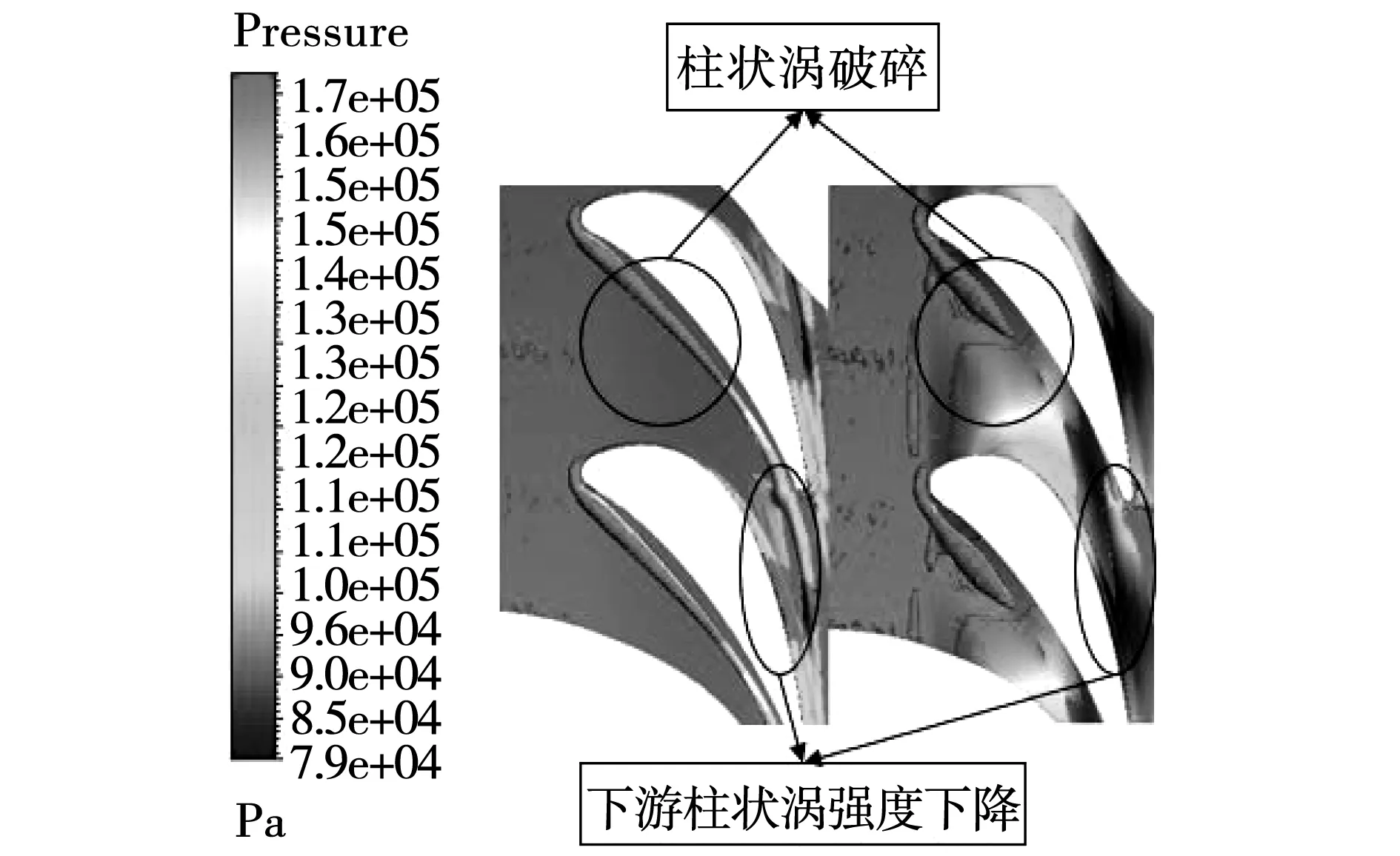
图14 原型叶栅与非轴叶栅漩涡结构对比图

图15依次为10%轴向弦长、50%轴向弦长和90%轴向弦长平面以Q准则显示云图。与原扇形叶栅对应Q准则显示云图相比可以看到上端壁各涡系结构强度均有所下降，至于下端壁处由于造型没有变化，所以无明显影响。通过以上Q准则的涡系结构云图，可以发现上端壁非轴造型确实降低了涡系结构强度。但需要注意的是0.9倍轴向弦长处，由Velocity Invariant Q显示图可知，在这个区域处上端壁有两个涡系结构，这是由于非轴造型凹凸的结构会影响到马蹄涡的提前分离、两个分侧的提前汇合以及后续涡系结构的演化从而使得涡系结构强度和数量发生改变。

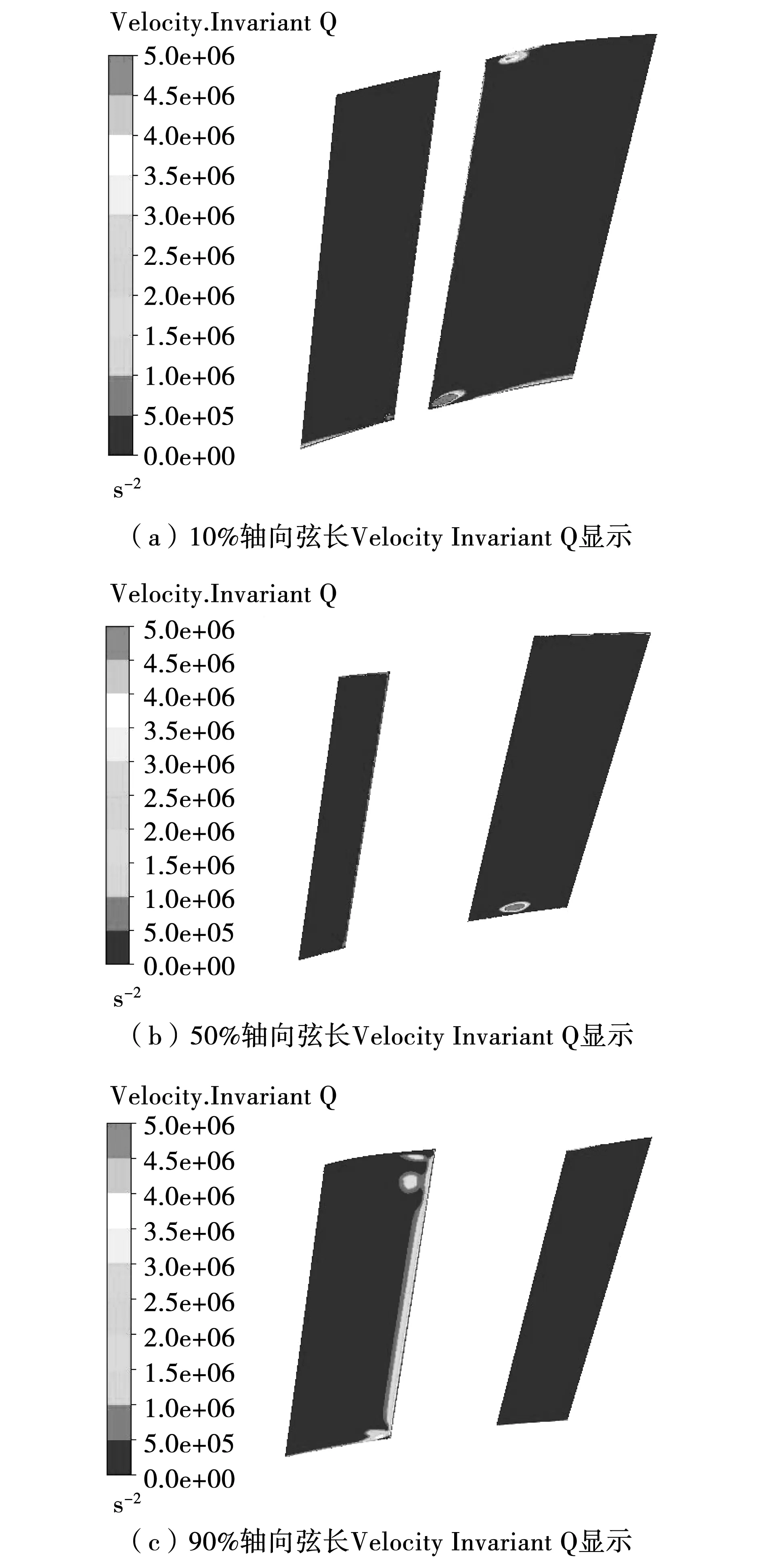
图15 轴向弦长Velocity Invariant Q显示

3.4 非轴造型损失分析

图16分别为原扇形叶栅出口能量损失云图和非轴端壁出口能量损失云图。出口位置取距尾缘40%轴向弦长处。由两对比图结合前文可知叶栅后半部分附面层由于压力梯度的降低，可以看到非轴造型和原扇形叶栅对比上端壁附面层整体尺度变得小，这也就意味着非轴造型上端壁的附面层损失变得更小了，相应损失得到降低。同时由图可以发现上半叶高区域处低损失面积增大，高损失面积减小，集中脱落涡结构下移，峰值和面积略有变化，这进一步印证上端壁附近处涡系结构的强度和所处位置的改变。下半叶高区域处低损失面积和高损失面积变化不大，集中脱落涡结构位置上没有大的变化，峰值和面积略有减小，这样的结果表明上端壁改造结果对下端壁影响甚微。

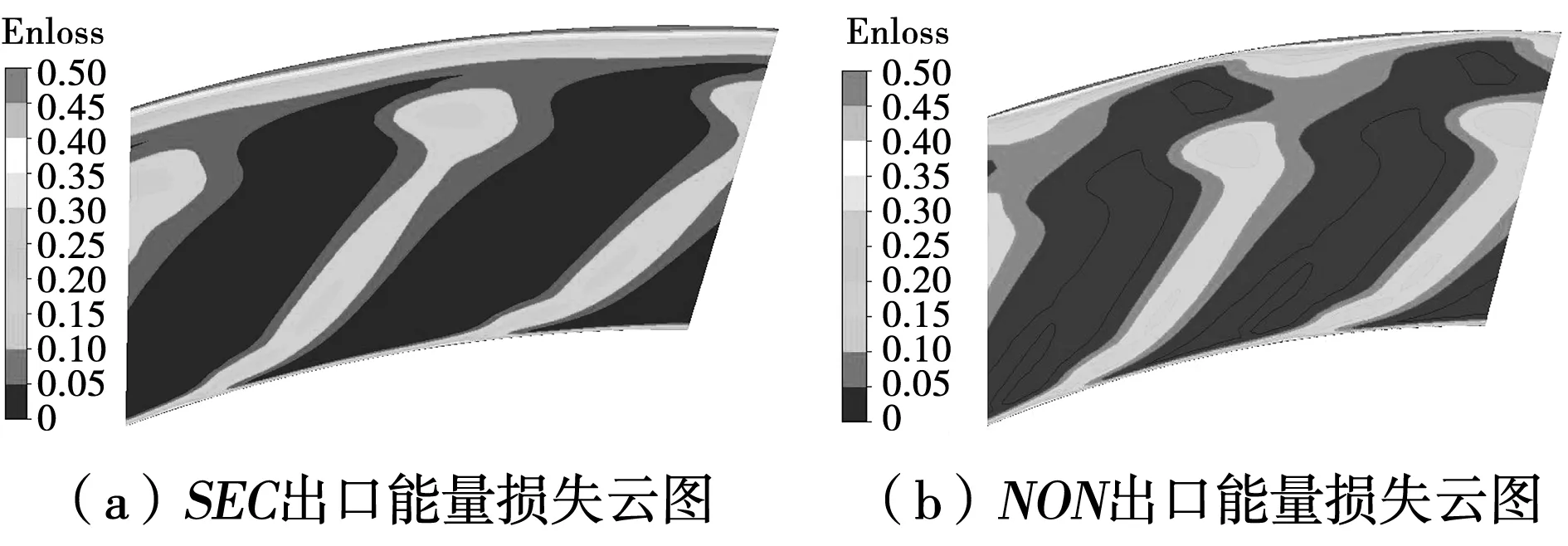
图16 出口能量损失云图

通过在Ma=0.9下的实验非轴造型叶栅和原扇形叶栅平均能量损失相对减小18.2%，数值模拟情况下非轴造型叶栅和原扇形叶栅总参数平均能量损失相对减小16.4%。进一步印证了上面对非轴端壁减低损失的分析。

4 结论

(1)通过Bezier曲线在流向控制线上分布8个控制点完成扇形叶栅上端壁非轴端壁的构建。同时为了通过数值模拟结果进行流场结构分析，所以基于能量损失系数以及总压损失系数沿叶高方向上的分布对数值模拟做了验证。

(2)进行了对非轴造型和原扇形叶栅关于型面静压分布的对比分析，对比发现上端壁非轴端壁造型基本对50%叶高以下区域流动影响很小，主要影响区域在上半部叶高，在相关轴向区域内起到改变横向压力梯度的作用。

(3)通过流动特性分析以及建立上端壁流线云图对比分析了原扇形叶栅和非轴端壁的流场结构，非轴造型影响了叶栅端壁的涡系结构产生位置的偏移以及分离和汇合时间的改变。通过建立Velocity Invariant Q显示图在轴向上五个位置与原扇形叶栅进行了对比分析，同时结合出口截面能量损失云图分析表明非轴端壁造型在叶栅前半部分降低损失主要通过削弱涡系结构的强度。叶栅后半部分通过减小横向压力梯度改善了流场性能，减小附面层厚度降低损失。

(4)通过在不同马赫数条件下对非轴造型和原扇形叶栅进行了数值模拟计算得到了上端壁非轴造型更为精准的影响区域在40%以上，其中部分区域损失略有增加但大部分损失降低。通过三种马赫数条件下的出口损失云图和平均能量损失可以得到非轴造型通过减小端壁附面层的厚度以及削弱涡系强度，达到了降低能量损失的目的。最后基于本文扇形叶栅进行上端壁非轴造型能够达到降低15%左右的能量损失。