基于CAPSO-RBF的磁悬浮系统控制研究

贾涌槟，李丹菁

(上海应用技术大学电气与电子工程学院，上海 201418)

0 前言

磁悬浮技术是让被控对象保持在一个悬空且相对静止的状态下，处在这种状态下的被控对象没有与其他物体发生接触，所以就避免了因摩擦造成的损耗，很大程度上降低了维护成本。因此，无论在国防、制造业、交通，还是其他各个领域，磁悬浮技术都有着很大的发展空间。

磁悬浮球系统因结构简单、成本低、易于实现等特点成为磁悬浮技术领域广泛的研究实验平台，但磁悬浮系统由于非线性和滞后性等特性使得系统的稳定性较差，易受外界因素干扰。因此，设计一个可靠并且高效的控制器使磁悬浮系统有较好的稳定性和快速性是该领域研究重点。

磁悬浮球系统控制策略主要分为传统控制和智能控制，传统控制主要有PID控制、模糊控制、自适应控制以及混合控制等[1-2]，其本质都要建立控制对象的数学模型，然后设计一个数学形式的控制器以达到控制目的；而智能控制是利用仿生算法或者模拟人脑的逻辑思维模式去控制系统，主要采用神经网络，而不同的神经网络各有利弊[3]。在径向基函数(Radial Basis Function，RBF)神经网络研究方面，文献[4]用RBF改进了在线辨识的自适应PID控制算法；文献[5]设计并实现了神经网络结合模糊滑模控制系统，该系统具有速度跟踪性能与鲁棒性；文献[6]设计并实现了RBF神经网络自适应状态反馈控制器。在粒子群算法优化神经网络研究方面，文献[7]基于粒子群优化(Particle Swarm Optimization，PSO)结合梯度下降算法优化RBF磁浮列车温度补偿模型参数；文献[8]证明了云自适应算法能有效优化RBF网络；文献[9-10]在图像领域，通过云自适应粒子群优化(Cloud Adaptive Particle Swarm Optimization，CAPSO)算法减少了运算量，提高了搜索精度；文献[11]在电力作业风险态势感知上采用了云自适应粒子群优化脉冲神经网络的方法。在控制领域中，文献[12-13]采用改进的CAPSO算法优化BP神经网络；文献[14]设计并实现了自适应粒子群优化算法用于修正炮弹分数阶控制器。采用云自适应粒子群算法的神经网络控制器设计方面缺乏理论依据，并且磁悬浮球系统具有非线性特点，因此，如何设计利用云适应粒子群算法的神经网络控制器成为一个难题。

本文作者针对磁悬浮球系统，设计云自适应粒子群优化后的RBF神经网络控制器。该方法采用一个PD控制器作为RBF神经网络的“教师”控制器，RBF神经网络控制器对整定后的PD控制器的输出进行学习，再结合云自适应粒子群算法优化RBF网络3个参数以对控制精度进行补偿，达到由CAPSO-RBF控制器主导控制效果，使被控对象实现更快速、准确、稳定悬浮的目的。

1 磁悬浮系统的数学模型

1.1 磁悬浮系统的硬件组成与参数

实验装置分为装有数据采集卡的PC机和磁悬浮球装置两个部分。其中，磁悬浮球装置包括电磁铁、光电位置传感器、电源、功率放大器、补偿器、钢球、LED等部件，其系统硬件实体如图1所示。

图1 磁悬浮球装置系统硬件实体

磁悬浮球装置参数的具体数值如表1所示。

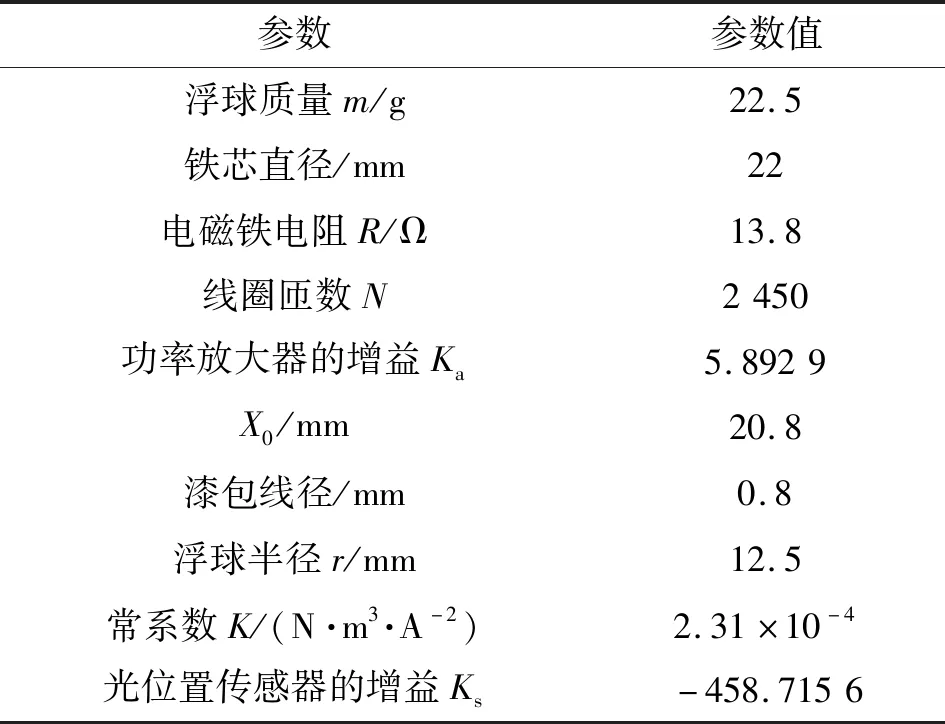
表1 磁悬浮球装置参数

1.2 系统模型建立

建立系统的物理模型需要忽略一些影响不大的干扰因素并考虑系统物理变量之间的实际问题，再进行理想化假设以便建立出切合实际的物理模型。假设：磁通全部穿过外部；磁通分布均匀；气隙磁阻抗相对汇合；钢球所受的电磁力集中在质心。

假设只存在两个力，一个是电磁铁的吸引力，另一个是被控对象的重力，其动力学方程为

(1)

其中：x为钢球重心离磁铁下端表面的距离，m；m为钢球质量，kg；F(i,x)为电流经过线圈产生的电磁力，N。

根据基尔霍夫定律、能量守恒定理，被控对象受到电磁铁的力为

(2)

其中：μ0=4×10-7H/m，μ0为空气磁导率；KfA为小球截面的导磁面积，m2；N为电磁铁线圈匝数；x为电磁铁磁极表面到被控对象重心的间距，m；i为电磁铁绕组中的瞬时电流，A。因μ0、A、N为常数，故可定义一个常系数K:

(3)

由式(2)可以看出磁悬浮系统为非线性系统。

在研究磁悬浮的一些特性后，因为磁悬浮系统的控制目的是让被控对象在一定范围内受力平衡，所以可以将其非线性部分利用小偏差法进行线性化处理。

又因为磁悬浮系统的控制属于弹性控制，可以在被控对象保持稳定悬浮的点(i0,x0)处对其进行线性化处理。将式(2)按泰勒级数展开并保留前几项得：

F(i,x)=F(i0,x0)+Fi(i0,x0)+

Fx(i0,x0)(x-x0)

(4)

其中:

(5)

故完整描述此系统的方程如下:

(6)

其中：Ki是钢球稳定点处电磁引力F对电流i的刚度;Kx是稳定点处电磁引力F对空气间隙x的刚度。

设此实验装置的输入为功放的输入Uin，系统输出为Uout，则系统方程式(6)经过拉氏变换后代入边界方程得开环传递函数：

(7)

其中：Ks为光位置传感器的增益；Ka为功率放大器的增益。磁悬浮系统的状态方程为

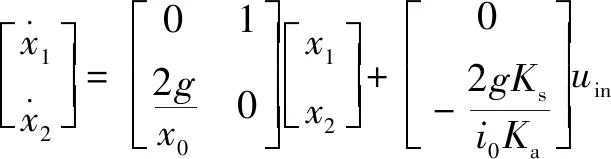
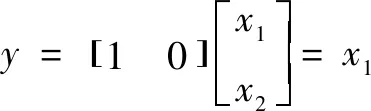
(8)

将实际参数代入式(8)后系统的状态方程为

(9)

2 RBF神经网络

2.1 径向基函数神经网络的模型

RBF神经网络由三层组成，如图2所示，用“基”构成隐含层，输入不需要通过权值连接可直接映射到隐含层。当RBF的中心点确定后映射关系随之确定。输出是隐含层单元输出的线性加权和，所以隐含层到输出层的映射是线性的，此处的权即为网络权值。利用核函数的思想，网络由输入到输出的映射是非线性的，而网络输出与网络权值是线性关系，从而使网络学习速率加快并且避免落入局部最优问题。

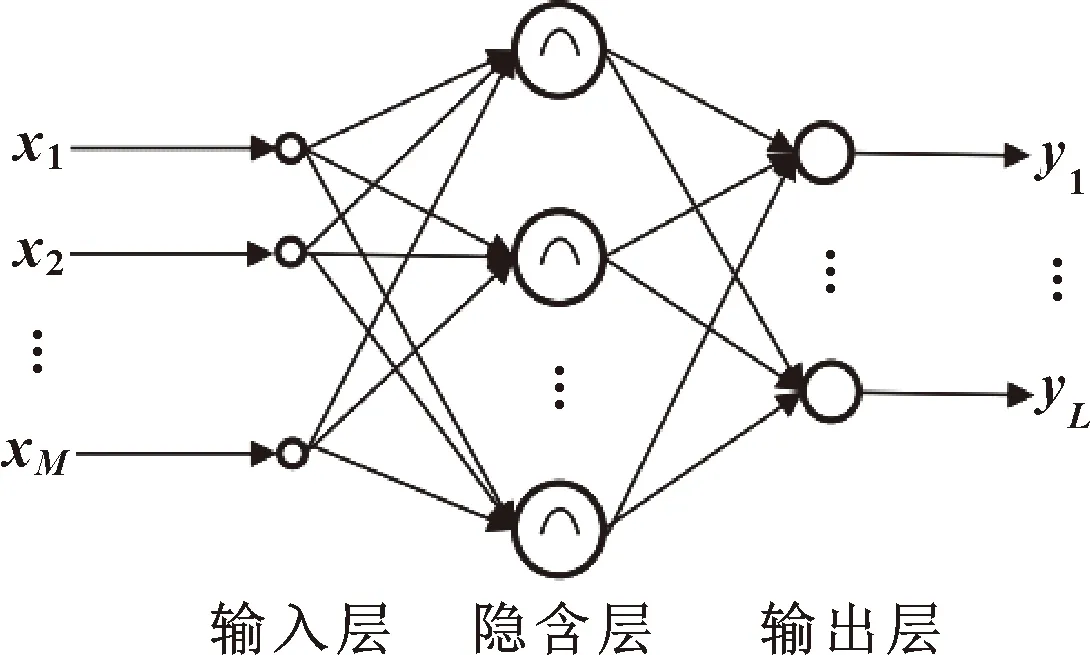
图2 RBF神经网络结构

2.2 径向基函数神经网络的输出

设网络输入x的维数为M，输出y的维数为L，输入样本对的长度为N。

因为RBF神经网络的输入层到隐含层的映射x→ui(x)是非线性的，使用高斯函数为激活函数的RBF网络隐含层第i个节点输出可表示为

(10)

式中：ui为第i个隐含层节点的输出;δi为对应的标准化常数;隐含层的节点数量为q，x=[x1,x2,… ,xM]为输入样本;ci为对应隐含节点的高斯中心向量,c=[ci1,ci2,… ,ciM]T，节点输出的范围为(0,1)，当x=ci时ui=1，RBF神经网络隐含层到输出层ui(x)→yk的线性映射即为

(11)

2.3 RBF神经网络监督控制

采用一个PD控制器作为RBF神经网络控制器的“教师”。首先让RBF神经网络控制器对PD控制器的输出进行学习，再结合CAPSO优化RBF网络，最后达到由CAPSO-RBF控制器主导控制的效果。系统结构如图3所示。

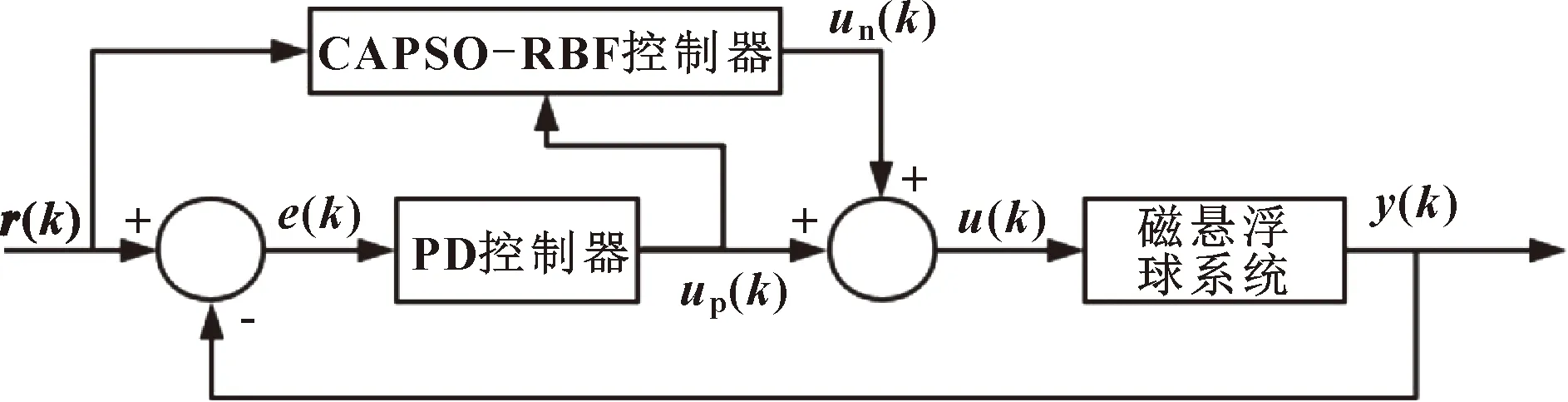
图3 基于CARBF神经网络控制的磁悬浮系统结构

图3中，r(k)为神经网络的输入，高斯函数为RBF神经网络隐含层的激活函数。经调试，隐含层采用4个隐含单元，设CAPSO-RBF神经网络控制器的输出为un(k)。隐含层隐含单元的输出为hi：

(12)

其网络连接权值为wi(k)(i=1,2,3,4)，则RBF网络的输出为

(13)

控制率为

u(k)=up(k)+un(k)

(14)

其中:w=[w1,w2,w3,w4]T，需要学习的参数有3个：中心向量c，标准化常数σ，网络权值w。

经整定,PD控制器的控制参数取kp=20、kd=0.28时,能使磁悬浮球悬浮。

3 基于云自适应的粒子群算法RBF神经网络控制

3.1 粒子群算法

粒子群算法是模拟鸟群捕食而发展起来的基于群体协作随机搜索的算法，用于解决优化问题，每个需优化问题的解相当于搜索空间里的一只鸟，称为“粒子”。而所有的粒子都有一个被优化函数所定义的适应度，适应度越大越好，并且每个粒子都有一个速度来决定它们的方向和距离，再通过迭代更新自己的位置。

(15)

其中:d表示向量的维数;ω表示惯性权重;k表示迭代次数；c1和c2表示学习因子。

采用粒子群优化算法对RBF控制器的中心向量、标准化常数、网络权值3个参数进行寻优，进一步提高RBF神经网络控制器的整体性能。

3.2 云自适应粒子群算法

传统的粒子群搜索算法中的惯性权重和学习因子参数设置更新简单，会导致整个网络优化速度减慢、寻优精度降低，更或者使算法陷入局部最优。本文作者利用动态自适应思想优化惯性权重、学习因子，以解决以上问题。

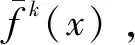
(16)

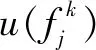
(17)

学习因子c1、c2为改变粒子群算法中粒子之间信息交换的能力，进行动态自适应调节,可提高算法寻优速度。

c1=c1max-k(c1max-c1min)/K

(18)

c2=c2max-k(c2max-c2min)/K

(19)

其中:[cmin，cmax]为学习因子c的取值范围;K为迭代总次数。

在寻优前期要保证寻优速度，设定c1>c2；到寻优后期,算法接近收敛,设定c1

采用云自适应算法优化的粒子群算法在全局寻优能力上得到提升，收敛速度更快且避免了陷入早熟收敛和局部最优所导致的精度下降问题。

3.3 云自适应粒子群算法优化RBF控制器

传统的径向基函数神经网络是采用聚类算法得到基函数，然后通过最小二乘法得到连接权重，这种方法导致前两个参数和连接权重失去内在联系。为解决这类问题，本文作者采用云自适应粒子群算法对学习PD控制器输入后的RBF神经网络控制器的中心向量、标准化常数、连接权重3个参数进行编码归一优化。

设粒子种群规模为20，迭代次数为250次。其中，适应度函数控制RBF神经网络的预测精度，把每个粒子个体误差作为适应度函数f(x)，计算公式如下：

(20)

基于云自适应粒子群算法优化(CAPSO)的RBF神经网络监督控制器设计流程如图4所示。

图4 设计流程

4 设计仿真

在仿真实验中选择3种输入信号测试系统的信号跟踪性能，分别为8 mm阶跃输入、周期为1 s峰值为8 mm的方波、周期为1 s峰值为8 mm的正弦波。PSO-RBF与CAPSO-RBF 2种控制算法的测试结果如下：

(1)8 mm阶跃输入

图5所示为2种方法的阶跃响应结果。可知：加入了云自适应粒子群算法的神经网络控制器的磁悬浮控制系统响应速度非常快，迭代100次时误差稳定在7%。并且在0.15 s左右就达到了稳定状态，在快速性上比PSO-RBF快了2倍，并且没有超调。

图5 阶跃响应结果与收敛结果

(2)周期为1 s峰值为8 mm的方波

图6所示为2种方法的方波输入响应结果。可知：云自适应粒子群算法控制的系统在对方波信号的跟踪方面也表现得十分出色，当方波从+8 mm阶跃到-8 mm时无超调量，稳定时间也缩短为0.6 s，迭代60次时误差已经小于7%，但准确性指标稍欠缺。

图6 方波输入响应与收敛结果

(3)周期为1 s峰值为8 mm的正弦波

图7所示为2种方法的正弦波输入响应结果。可知：云自适应粒子群算法控制的系统对正弦波输入的响应较好，输出完全跟随输入，使得系统保持在稳定状态。

图7 正弦波输入响应与收敛迭代次数

云自适应粒子群算法结合RBF网络的梯度下降算法全局收敛速度快的优点，能够有效提高系统控制效果。对比3种算法在相对稳定下的控制性能，结果如表2所示。可知：加入云自适应算法后的RBF神经网络控制效果最好。

表2 3种算法控制性能比较

5 结论

针对磁悬浮球系统，本文作者设计了基于云自适应粒子群算法优化的RBF神经网络监督控制器。其中，粒子群算法对RBF网络的3个参数进行了量纲一化，云自适应算法改善了粒子群算法的早熟问题。采用原有RBF神经网络梯度下降法、粒子群算法、云自适应粒子群算法进行训练仿真并与所提方法进行对比。结果表明：加入2种智能算法耦合的RBF神经网络控制器凭借优秀的学习与自适应能力，使得磁悬浮球系统在动态性能和稳态性能上有较大的提升。