多辊连续矫直对高强钢残余应力分布的影响

陈 壮，丁文红，孙 力 ，张志强，刘天武

(1.武汉科技大学省部共建耐火材料与冶金国家重点实验室，湖北 武汉，430081；2.河钢集团钢铁研究总院，河北 石家庄，050023；3. 河钢集团邯钢公司技术中心，河北 邯郸，056002)

近年来，随着控轧控冷工艺的快速发展以及对高品质高强钢带材需求量的不断提升，加工过程中钢板内部产生的残余应力已成为制约生产效率和产品质量的关键问题之一[1-2]。为修正轧后板形缺陷以及减小甚至消除板内残余应力，国内一些大型钢铁企业斥巨资引进德国 MDS、SMS-Demag 和日本 MHI 等国际知名冶金设备公司的先进矫直设备对轧后钢板进行矫直处理。

多辊矫直是通过对板材施加逐步递减的交替弹塑性弯曲变形来消除板形缺陷。矫直过程中，钢板内部残余应力会随着钢板弹塑性弯曲而不断演变。Ataka[3-4]通过大量实验发现当塑性变形量超过70%时钢板矫直效果大幅提高，同时，当带钢形状不良时，最合适的矫直方法是：前两道次采用较大的弯曲曲率进行平行压下矫直，待曲率均匀化后，第三道次采用倾斜矫直使残余曲率逐渐收敛为0。荒木甚一郎[5]根据弯曲曲率几何关系对带钢矫直过程进行分析，发现当带钢原始曲率越大、矫直压弯量越大以及矫直辊数量越多时，矫直后带钢的不平度越小。Doege等[6]建立了成型过程分析模型来描述带钢多辊矫直过程，并提出了初始残余应力评价方法及相应的消除原理。詹光曹[7]研究了矫直道次对钢板残余应力的影响，结果显示，适当增加矫直道次有助于降低钢板宏观残余应力，从而改善板型质量。赵志毅等[8]采用盲孔法测定了不同矫直工艺处理后带钢中残余应力的分布情况，分析了矫直工艺对钢板残余应力分布的影响。刘东冶[9]采用ANSYS有限元软件中LS-DYNA模板建立了七辊矫直过程的三维动态仿真模型，重点分析了带钢矫直过程中的应力演变方式。目前的研究主要集中于带钢矫直过程中塑性变形规律及其表面残余应力变化，无法全面表征沿钢板厚度方向上残余应力分布的整体变化趋势，此外，关于残余应力分布对矫直后钢板在后续加工和使用中畸变行为影响的研究也报道较少。

基于此，本文以620JJ搅拌罐体用钢为研究对象，采用裂纹柔度法测定了原始钢板及经过多辊连续矫直后的钢板沿厚度方向上的轧向残余应力分布，提出了影响下游剪切过程材料畸变的残余应力评价指标，分析了矫直前后钢板内部残余应力的变化趋势，以期为后续矫直工艺参数的合理制定提供参考。

1 试验材料及方法

1.1 试验材料

实验用钢为某钢厂提供的搅拌罐体用钢620JJ的原始热轧板和矫直板，板厚为2.75 mm，宽度为1500 mm，其化学成分如表1所示。

表1 620JJ钢的化学成分(wB/%)

1.2 残余应力测试方法

对于620JJ原始钢板和经过矫直工序的钢板，均沿钢板宽度方向从操作侧开始，以带钢宽度1/2为对称中心，分别在1/16、1/8、1/4、1/2位置处取样作为残余应力测试样，试样尺寸为60 mm×50 mm×2.75 mm，依次标为A、C、E、G、I、K、M点，取样位置如图1所示。

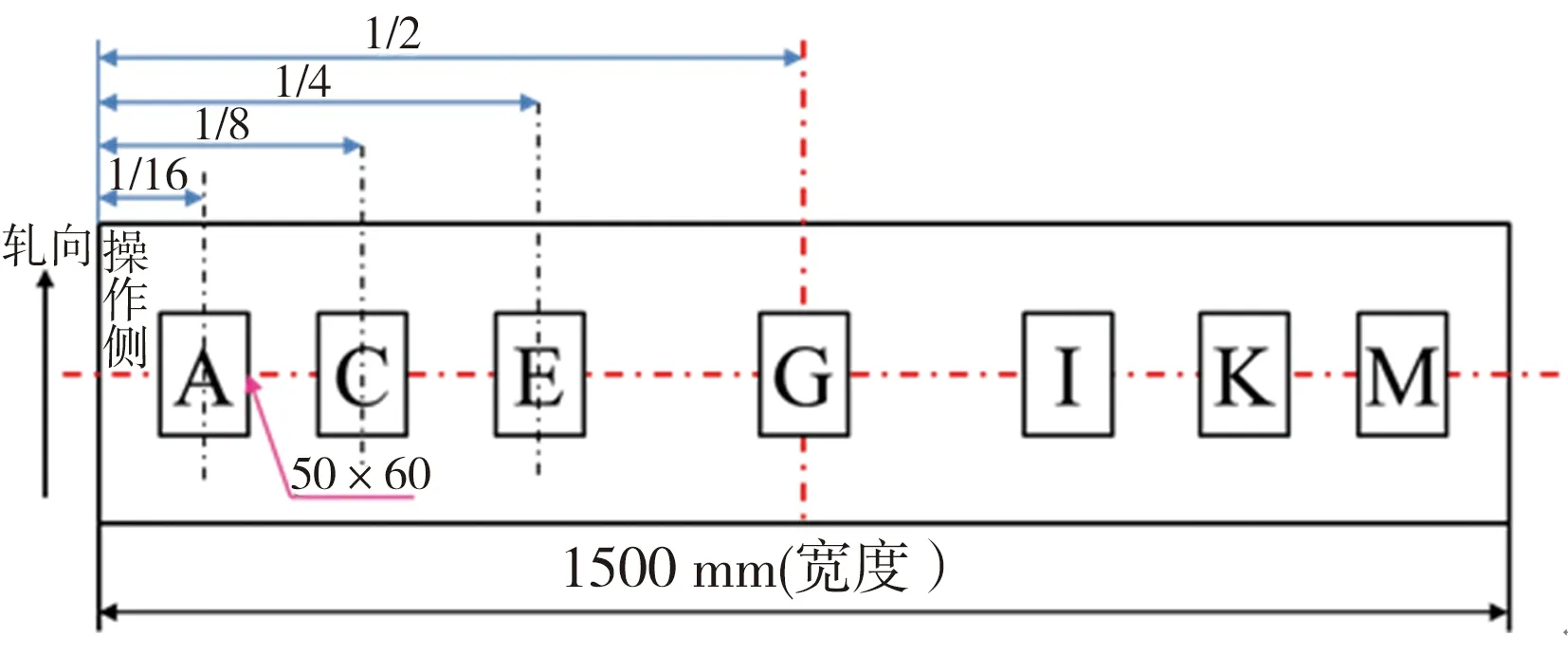
图1 取样位置示意图

采用基于弹性断裂力学原理的裂纹柔度方法(CCM)测试样品的残余应力，以表征材料沿厚度方向的轧向残余应力分布，测量时，通过引入逐渐增加深度的狭缝以释放测试平面上的残余应力，并且记录由残余应力释放所引起的变形，采用Abaqus和Matlab软件反演计算得到材料内的残余应力分布，测量原理示意图见图2。Prime[10-11]详细描述了本文所采用的特定应力计算程序。为降低测量时的附加应力，使用电火花线切割机(EDM)进行增量切割，其中钼丝直径为0.18 mm，切口宽度为0.20 mm。从附着于BE120-3AA箔式电阻应变计(酚醛-缩醛基底，康铜箔)的商用桥式应变指示器读取所释放的应变，敏感栅格尺寸为2.8 mm×2.0 mm。矫直试样切口以0.11 mm的增量切割至最终深度为2.53 mm。

图2 裂纹柔度法应变测量示意图

2 结果与分析

2.1 带钢沿厚度方向上的轧向残余应力分布

图3为原始钢板与矫直后钢板沿厚度方向上的轧向残余应力分布。由图3可见，原始钢板内部残余应力曲线大多呈“W”型，即沿中性面(1.5 mm附近)呈对称分布，同时中性面处残余应力值一般为曲线顶点，即应力最大值。经过矫直后，钢板内部残余应力大致呈“N”型分布，残余应力曲线一般有两个拐点，极大值一般在0.75 mm左右，极小值一般在2.125 mm附近。

为具体分析厚度方向上的轧向残余应力分布，特对表面残余应力进行定义：钢板线切割由下表面开始至上表面结束，故残余应力曲线的第一个点(起始点)对应下表面的残余应力，残余应力曲线最后一个点(终末点)对应上表面的残余应力。

表2列出了原始钢板和矫直后钢板不同测点对应的上、下表面残余应力值。由表2可见，原始钢板上、下表面均存在较大的残余应力，且呈现非对称分布，上表面最大和最小残余应力差值为572.35 MPa(对应E点和M点)，下表面最大和最小残余应力差值为437.84 MPa(对应M点和K点)，可以看出，上、下表面残余应力波动范围均很大，原因可能是在热轧快速冷却过程中，上、下表面水量比设置不合理，导致上、下表面的冷却速度不一样，在钢板各区域不同温度应力和组织应力的共同作用下，使得钢板内部存在较大的残余应力。

(a)测试点C (b)测试点E

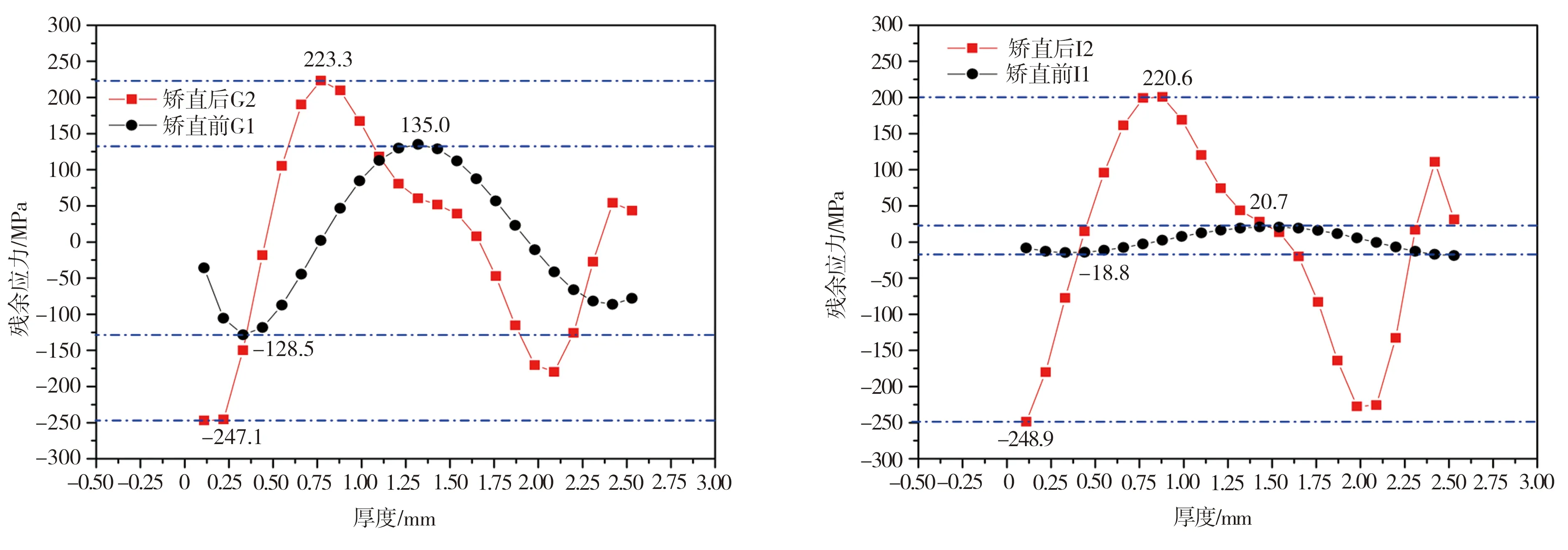
(c)测试点G (d)测试点I

(e)测试点K (f)测试点M

钢板经过多辊矫直后，上表面最大和最小残余应力差值为411.63 MPa(对应A点和M点)，下表面最大和最小残余应力差值为294.45 MPa(对应A点和K点)，上、下表面的残余应力分布均匀性有所改善，但在原表面残余应力较小的部位，表面残余应力水平出现恶化现象。矫直过程中，钢板发生弹塑性变形，消除了初始残余应力的同时也会引入一部分应力。若矫直机参数设置不当，则会对钢板表面残余应力分布产生不利影响。对于初始残余应力较大的点位(如C点和M点)，矫直后钢板表面残余应力急剧减小，矫直过程引入的应力与初始残余应力的消除程度相比，并不算大，矫直后对应位置的表面残余应力呈下降趋势；但在初始残余应力较小的点位(如I点)，矫直过程所引入的应力大于消除的初始残余应力，矫直后该点的表面残余应力反而会出现增大现象。

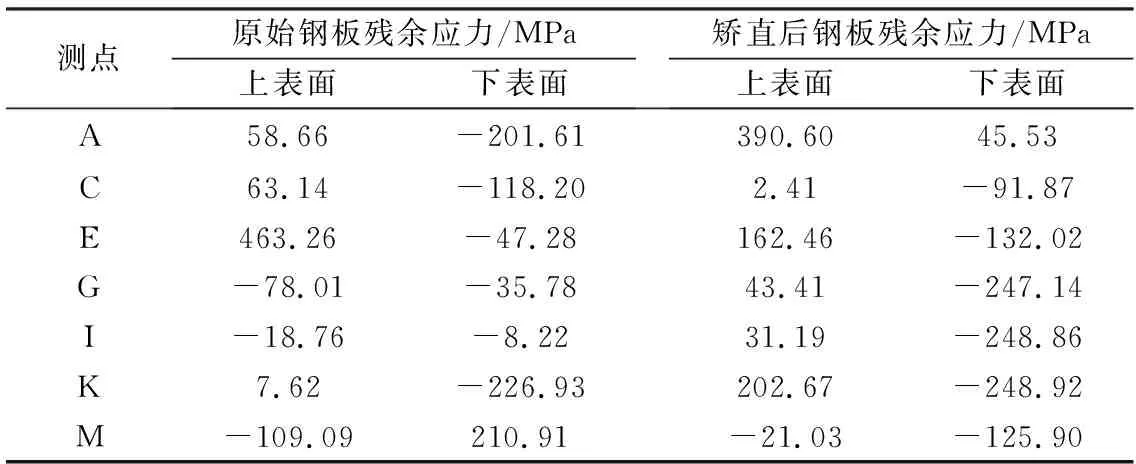
表2 矫直前后带钢各点的表面残余应力

2.2 带钢沿宽度方向上的轧向残余应力分布

图4为原始钢板和矫直后钢板沿带钢宽度方向的上、下表面残余应力分布。由图4可见，矫直前后，钢板上表面残余应力波动区间由463.26～-109.09 MPa变化到390.6～-21.03 MPa，上表面最大残余应力与最小残余应力差值由572.35 MPa减至411.63 MPa，降低了28.08%，波动区间减小；下表面残余应力波动区间由210.91～-226.93 MPa变化至45.53～-248.92MPa，下表面残余应力最大值与最小值差由437.84 MPa减至294.45 MPa，降低了32.75%，波动区间也显著减小。

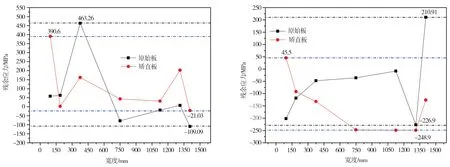
(a)上表面 (b)下表面

为更准确地描述原始钢板和矫直后钢板宽度方向上各点的残余应力变化，本文定义了两个残余应力的表征参数：厚度方向上轧向残余应力的绝对值(|δRS|)和轧向残余应力在厚度方向上的弹性应变能(ERS)。二者均采用了提取某一点残余应力水平的分析方法，是表征带钢宽度方向上应力分布的基础。

|δRS|是指材料上某点在厚度方向上最大残余应力δmax和最小残余应力δmin之间差值的绝对值，即|δRS|=|δmax-δmin|，用来衡量某点在厚度方向上残余应力的最大幅值，表征局部残余应力的不均匀程度。

弹性应变能(ERS)是对厚度方向上轧向残余应力的绝对值积分后所得，是带钢沿厚度方向上轧向残余应力形成过程中储存在带钢内的单位应变能，可用于描述某点在厚度方向上轧向残余应力的总体水平，可由式(1)描述：

(1)

表3列出了原始带钢和矫直后带钢各点的|δRS|和ERS计算值，为更直观地反映带钢沿宽度方向残余应力变化情况，特绘制相应的|δRS|和ERS随宽度的关系曲线如图5所示。结合图5和表3可知，与原始钢板相比，矫直后带钢|δRS|最大值与最小值之差由559.43 MPa降至430.75 MPa，波动范围降低了23.0%，而ERS最大值和最小值之差由245.42 MPa·mm降至207.49 MPa·mm，波动范围降低了15.46%。另外，经过矫直后，试样A、C、E、M四点的弹性应变能ERS有所减小，而G、I、K三点的ERS相对增大，相比于原始钢板，矫直后A、C、E、G、I、K、M处ERS的变化幅度依次为：-15.05%、-42.11%、-27.20%、43.46%、830.56%、34.17%、-15.82%。

表3 矫直前后带钢沿宽度方向不同位置的|δRS|和ERS值

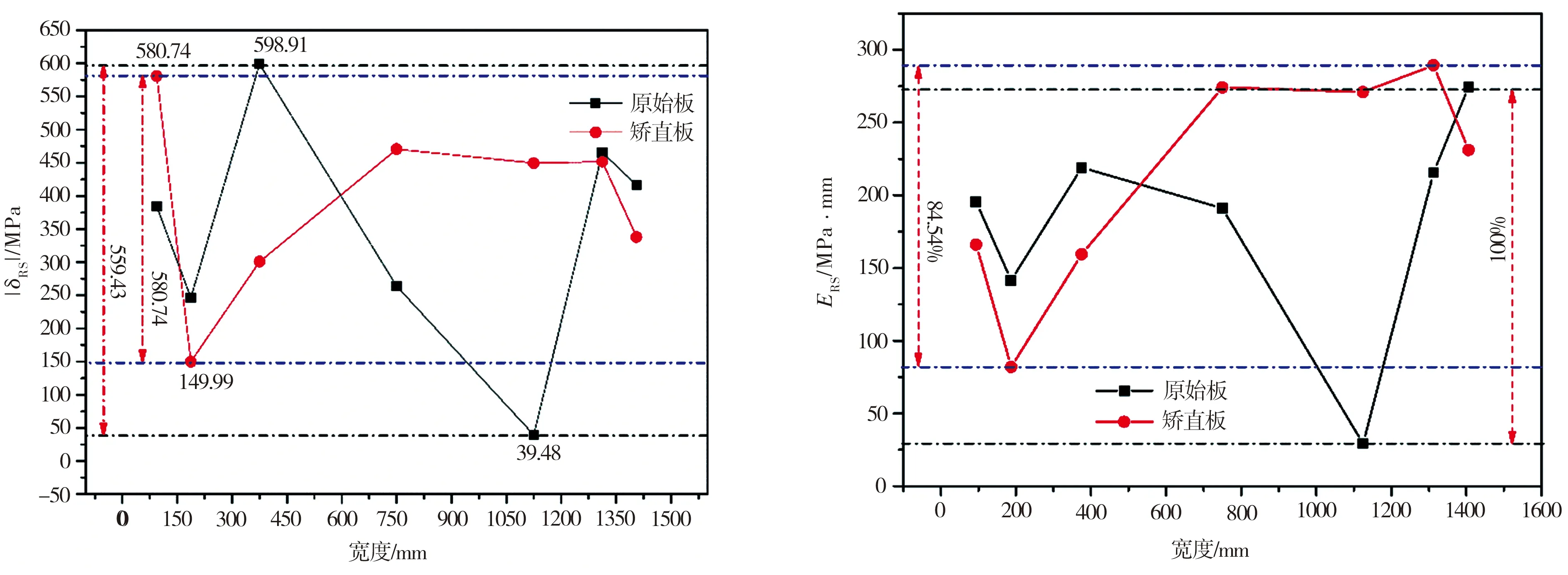
(a)|δRS| (b)ERS

由此可见，钢板经过多辊连续矫直后，沿宽度方向上残余应力分布的均匀程度整体上有所改善；而钢板某些部位残余应力水平的增加，这可能是因为矫直过程中大量应力伴随着钢板弯曲变形而引入。若将矫直前带钢内部的残余应力称为初始残余应力，多辊连续矫直过程中引入的残余应力称为多辊残余应力，那么带钢在矫直后总残余应力可以分为两部分：多辊连续矫直过程中引入的多辊残余应力和弹性区的初始残余应力[12]。矫直过程中，矫直参数设置不合适、板材初始残余应力小或引入的多辊残余应力过大均可能会导致矫直后钢板局部的残余应力增大。

3 讨论

3.1 带钢厚度方向上残余应力对称度分析

板带材在后续加工和使用过程中经常会产生翘曲畸变，其主要表现为：沿轧向的纵向翘曲(工厂称之为L翘)、沿宽度方向的横向翘曲(工厂称之为C翘)以及两个方向翘曲共存的四角翅，这主要是由钢板沿厚度方向上残余应力不均匀分布引起的[13]。为表征多辊连续矫直对带钢厚度方向上残余应力分布的影响以及衡量钢板的抗翘曲畸变能力，本文定义了一个评价指标:上、下表面应力不平衡度BT，可由式(2)表示：

(2)

式中：σTOP和σBOT分别为钢板上、下表面的残余应力值，MPa；σS表示钢板屈服强度，σS=607 MPa。

表4列出了矫直前后带钢厚度方向上的残余应力不平衡度计算值。从表4可以看出，经过多辊连续矫直后，钢板上、下表面的不平衡度平均值增加了20.95%；具体到各点位，A点上、下表面不平衡度增幅相对较小，增加了32.58%，而G点、I点、K点上、下表面的不平衡度增幅很大；C点、M点、E点上、下表面不平衡度则有所减小。由此可见，经过多辊连续矫直后，钢板厚度方向上残余应力对称度的平均值增大，多个点的残余应力不平衡度增加，表明矫直后钢板上、下表面应力的对称度出现恶化，亦即更容易在后续加工使用过程中发生翘曲畸变。

管奔等[14]提出，在矫直过程中，具有不同初始曲率的截面通过同一设备时必然具有不同的弹塑性变形历史，其应力演变过程是不一致的。轧制后钢板本身上、下表面残余应力呈不对称分布外加若矫直参数设置不当，矫直时上、下表面发生了不同程度的弹塑性变形，同时伴随着不同程度的弯曲，从而引入了不同大小的多辊矫直残余应力，这些因素的耦合作用导致了矫直后钢板上、下表面应力对称度的恶化，使得钢板更容易在下游工序中发生翘曲畸变。

表4 矫直前后钢板沿厚度方向的残余应力不平衡度

3.2 带钢宽度方向上单位长度残余应力变化

卢兴福[13]提出了钢板带裁切加工后侧弯变形的假设：轧制后钢板带塑性应变(主要是纵向塑性应变)会沿宽度方向呈不均匀分布，由于变形协调作用，在钢板带内部产生了不均匀的压应力，但其不足以引起钢板带翘曲变形，而经裁切加工后，钢板带纵向塑性应变不变，应力重新分布，这会导致钢板发生整体的屈曲变形，可能会生产出侧弯缺陷板。钢板带在下游裁切加工后的变形是切条宽度方向不均匀延伸所导致的整体屈曲变形的结果，为了衡量材料在下游剪切过产生侧弯的可能性，本文定义了一个参考量WT，表示宽度方向上单位长度残余应力，亦即相邻两点弹性应变能之差与距离的比值，可由式(3)表示：

(3)

式中：ERS1和ERS2分别表示1点和2点处的弹性应变能，MPa·mm；L1-2为1、2两点之间的距离，单位为mm。

表5所示为矫直前后沿宽度方向不同位置试样的单位长度残余应力计算值。由表5可见，钢板经过矫直后，其边部A-C部分单位长度残余应力WT增大了0.32 MPa，增幅为55.17%，K-M段的WT值则变化不大；矫直后钢板中部E-G段的单位长度残余应力显著增大，增幅为342.86%，G-I、I-K段的WT值明显降低，C-E段的WT值则保持不变。此外，矫直前后，钢板单位长度残余应力的最大值和最小值之差由0.93 MPa减至0.89 MPa。

由此可见，经过多辊连续矫直后，虽然钢板整体的残余应力水平有所上升，但残余应力分布的均匀性得到改善，钢板整体的单位长度残余应力分布相对均匀，使得其在后续使用过程中产生侧弯畸变的可能性减小。矫直过程中，工作辊对带钢不断施加正或负应力抵消了钢板内原有的反方向应力，使带钢发生弯曲变形，内部残余应力发生变化，若初始残余应力过大，矫直时很大程度上会被抵消，而过小的初始残余应力可能导致矫直后残余应力增大。

表5 矫直前后沿宽度方向不同位置带钢的单位长度残余应力

4 结论

(1)裂纹柔度法能很好地表征带钢厚度方向上的残余应力。原始板经轧制后，表面存在较大的残余应力，且残余应力沿厚度方向呈“W”型分布，上、下表面最大残余应力值分别为463.26、210.91 MPa；钢板经过矫直后，厚度方向残余应力呈“N”型分布，上表面呈拉应力状态，最大残余应力值为390.60 MPa，下表面大多呈压应力状态，最大残余应力值为-248.92 MPa。

(2)带钢经多辊连续矫直后，内部某些部位残余应力水平上升，但沿宽度方向上残余应力分布均匀程度有所改善。经过多辊连续矫直后，带钢靠中心至传动侧这一区域内的弹性应变能增加，但残余应力绝对值和弹性应变能的波动范围有所减小。

(3)带钢经多辊连续矫直后，上、下表面残余应力分布对称度减小，导致钢板更容易在后续使用过程中产生翘曲畸变。

(4)经过多辊矫直后，带钢整体的单位长度残余应力分布稍显均匀，这使得其在后续使用过程中产生侧弯畸变的可能性更小。