一类带参数的插值逼近型曲线细分
姚红丽, 张 莉, 檀结庆
(合肥工业大学 数学学院,安徽 合肥 230601)
0 引 言
近40年,细分方法是CAGD、CAD&CG的研究热点之一;给定一个控制多边形,根据选取的细分规则,通过计算机不断细化控制多边形,直接生成平滑的曲线曲面。由于细分方法适用于任意拓扑网格,在曲线/曲面重建以及几何造型中有着广泛的应用。
根据极限曲线是否通过初始控制点,曲线细分格式被分成插值型和逼近型2种。插值型细分格式直接插值初始控制点并按需产生新点,生成的极限曲线能有效保留目标曲线的细节特征。文献[1]提出经典的四点二重细分格式,并证明了生成的极限曲线可达C1连续;文献[2-4]提出不同的插值型细分格式。逼近型细分格式逼近初始控制多边形,其生成的极限曲线连续阶更高。文献[5]提出割角细分法,引起图形学届的广泛关注;文献[6-10]提出不同的逼近型细分格式,促进了细分方法的发展。为了将2种细分格式结合起来,文献[11]首次提出融合型细分,先利用逼近型细分格式计算出每步细分时的偏移量,再通过对参数的调整,从而实现对控制点的插值。采用参数调节的方法的文献也有很多。文献[12]从三次B样条曲线细分格式出发,推导出2种融合型细分格式并分析了其相应的连续性;文献[13]通过对融合型细分格式中参数变量的适当选取,从而衍生出具有良好性质的新格式,实现对极限曲线的形状调整;文献[14]提出一种非静态融合型细分格式并分析了其指数多项式的再生性;文献[15]对一类融合型三重细分格式的一系列性质进行了分析。然而,参数调节的过程是非常冗杂的。文献[16]“Interproximation”细分不仅能够将插值型和逼近型细分格式的优势有效地结合,而且避免了参数调节的冗杂过程;文献[17]推导出相应的几何规则,将四点插值和三次B样条细分格式结合起来,给出一种C2连续的插值逼近型细分格式;文献[18]通过相应的几何规则,将四点插值和切割磨光细分格式结合起来,给出一种C1连续的四点插值-切割磨光细分格式。
鉴于插值逼近型格式的优异表现,本文建立一个带双参数的插值逼近型细分框架。该框架既包含了一些已有的细分格式,还派生出一些新的细分格式。它的极限曲线既能插值部分点,同时又能逼近其余点,能有效地生成和复现复杂的几何图形。
在自然界中,很多几何图形的轮廓上既有一些尖锐的地方需要被插值,同时又有其他平滑的地方需要被逼近,如图1所示。
单一的插值型格式或是单一的逼近型格式都很难复现其轮廓曲线,而本文框架能够简单有效地复现其轮廓曲线。

图1 轮廓上的黄色圆点需要被插值,其余地方需要被逼近
1 预备知识
(1)
其中,系数a={ai}i∈Z被称为细分格式的掩模。
引理1[2]若细分格式(1)一致收敛,则
(2)
对细分格式应用z-变换,即
(3)
其中,a(z)被称为Laurent多项式。
2 带参数的插值逼近型细分框架
本节针对融合型格式调参过程复杂的缺陷,构造一类带参数的插值逼近型细分框架,该框架无需调参就能自如地插值指定点并逼近其余点。另外,本节还设置了插值点的选取规则,根据此规则,能自动筛选出插值点的位置。
2.1 细分框架的构建
在现有细分格式中,若想插值指定点并逼近其余点,融合型格式是一个比较合适的选择,融合型格式为:
(4)
在细分迭代过程中,不断产生新边点和新顶点。控制多边形的每条边所对应产生的新点被称为新边点,每个控制点所对应产生的新点被称为新顶点。参数γ是否为0对极限曲线的影响如图2所示。当γ=0时,(4)式退化成插值型格式;当γ≠0时,(4)式退化成逼近型格式。
插值型格式固定旧顶点的位置,生成新边点,呈向外扩张的趋势。逼近型格式移动旧顶点的位置,生成新顶点及新边点,呈向内收缩的趋势。
插值型格式和逼近型格式都有其自身独特的优势。然而在实际应用中,不仅要插值部分点,同时还要逼近其余点。因此,本文基于融合型格式,通过分段设置参数来满足实际应用需求。

图2 参数γ的影响效果
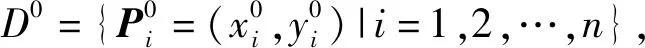

(5)

(6)

(7)

(8)
根据初始数据点集被分成插值点集DI和逼近点集DA,新点的产生有4种情形。若相邻两点都是插值点,则选用(5)式进行迭代,引入参数ω1;若相邻两点都是逼近点,则选用(6)式进行迭代,引入参数ω2、γ;若相邻两点中既有插值点,又有逼近点,则选用(7)~(8)式进行迭代。
设给定的初始控制多边形是不封闭的,其顶点为P0、P1、…、Pn,需要增加2个顶点P-1、Pn+1。一般地,这2个顶点的位置向量分别取P-1=P0,Pn+1=Pn或P-1=2P0-P1,Pn+1=2Pn-Pn-1,从而得到新增的2个顶点P-1、Pn+1。
2.2 插值点的选取规则

(9)
利用差分代替微分,从而实现对离散数据点曲率的计算[19]。
本文建立下列3类插值点选取法规则。
拐点:拐点是曲线的凹凸分界点。在实际应用中,曲率也用来判断拐点的位置。首先,点Pi两侧的曲率值变号,即K(ti-1)K(ti+1)<0;其次,点Pi的曲率值K(ti)∈(-ε,ε)或不存在。若上述2个条件同时被满足,点Pi为拐点。
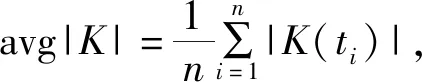

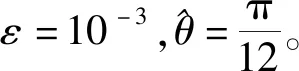
3 连续性分析
为了兼顾实际应用需求,本节给出参数具体的取值范围,使得(5)~(8)式生成的极限曲线达到C2连续。
引理2[20]假定局部细分矩阵的5个特征值λ0、λ1、λ2、λ3、λ4依次递减,其中λ0=1。若特征值满足(λ1)2=λ2,则该细分格式生成的极限曲线是C2连续的。

证明由上述分析可知,要证明本文细分框架(5) ~(8)式生成的极限曲线可达C2连续,即证(6)~(8)式生成的极限曲线可达C2连续。




(10)
综上所述,定理1成立。

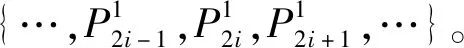

(11)
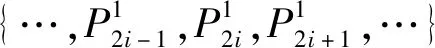
(12)


综上所述,定理2成立。
4 数值实例
本节给出一些数值实例,利用本文的细分框架以及插值点的选取规则来复现复杂图形的极限曲线,其中参数ω1=-1/16、ω2=0、γ=1/8。
如图3所示,由本文细分框架生成的极限曲线能够自如地插值正六边形的部分顶点。给定初始正六边形,任意指定插值点的位置和数量,并将其余点标记为逼近点,则生成的极限曲线能够自如地插值指定点。图3中:蓝色虚线表示初始控制多边形;红色实线表示生成的极限曲线;星形是插值点的位置。

图3 插值正六边形的部分顶点并逼近其余点
梅、兰、竹、菊4种植物的极限曲线如图4所示。图4中:黑实线和红实线分别表示初始控制多边形与极限曲线;蓝色、绿色、亮红色实心圆圈分别为极大曲率点、拐点、尖点的位置。

图4 4种植物的极限曲线
梅兰竹菊是诗画中最常见的题材,它们的造型各有特色。图4a通过采集植物轮廓的数据点来形成蓝色控制多边形;图4b利用本文提出的细分框架,插值植物花瓣、枝叶的边缘等特征点,生成极限曲线;图4c展示了梅兰竹菊的最终效果,其极限曲线不仅保留了细节特征,而且呈现了植物的美丽姿态。
以上实例说明了本文算法的灵活性,通过插值细节特征点,逼真地复现了上述复杂造型,通过在耐克Logo的几何轮廓上采取控制顶点,利用本文格式与文献[8-9,14]等4种格式分别进行迭代,复现耐克Logo的极限曲线。通过比较可以看出,本文格式生成的极限曲线更加贴合耐克Logo的几何形状,如图5所示。

图5 4种格式复现耐克Logo几何形状的对比
5 结 论
本文基于融合型细分格式,给出新顶点及新边点生成的几何规则,提出一类二重插值逼近型细分框架。该细分框架不仅包含了一些已有的经典细分格式,还派生出一些新型细分格式。它可以同时插值指定点并逼近其余点,且极限曲线是C2连续的。另外,本文还给出了一套插值点的选取法则,控制点集被分成插值点集和逼近点集。数值实例表明,本文所提出的细分框架能有效地生成和复现复杂的几何图形,其生成的极限曲线不仅能保细节特征,而且有良好的视觉效果。

