无人驾驶拖拉机田间路径规划方法研究

张炳力, 程啸宇, 程 进, 李傲伽, 郑平平

(1.合肥工业大学 汽车与交通工程学院,安徽 合肥 230009;2.安徽省智能汽车工程实验室,安徽 合肥 230009)

随着精准农业实施,无人驾驶拖拉机已成为研究热点,它的应用可解决农村劳动力不足等问题[1-2],而其规划路径的合理高效性将影响田间作业的精度和质量。根据环境信息掌握的情况,无人驾驶拖拉机路径规划可分为全局路径规划和局部路径规划。全局路径规划是在农田环境信息已知的情况下提前离线规划出全局路径,以实现对地块全覆盖,减少对地块不必要碾压,寻求最优解;局部路径规划是在环境信息未知的情况下,由感知传感器实时获取行驶路径周围障碍物信息进行在线路径规划,注重路径安全性与实时性[3-4]。

现阶段国内外关于拖拉机路径规划的研究较少。对于全局路径规划:文献[5]对地块最佳作业角展开研究,提出了“哈密顿路径搜索”和“几何推理”2种路径轨迹构建法;文献[6]将地块分割为若干单元,再利用遗传算法寻找最优覆盖路径;文献[7]以铁牛TN654为实验平台,联合田间作业方式和拖拉机自动导航系统的特点,对耕地和播种这2种作业轨迹进行设计。对于局部路径规划:文献[8-9]根据障碍物大小与农机作业宽度的关系划分障碍物,针对含大障碍物的地块,多通过“自上而下法”、“细胞分割法”等对地块进行分割和合并,提出一种折线避障措施避开小型静态障碍物;文献[10]提出最短切线避障路径构建方法,针对有静态障碍物的情况可快速规划出避障路径。目前,国内外对于全局路径规划的研究主要是针对规则地块在不同评价指标和不同作业方式下的路径规划,对不规则地块的全局路径规划研究较少,且缺乏一定的通用性。而现有局部路径规划多采用最短切线法和折线法[11-12],没有考虑农机作业宽度和最小转弯半径的存在,且避障策略过于简单，只考虑单个静态障碍物避障情况,没有对障碍物存在的不同情况进行系统性分析研究。

本文在现有研究的基础上,提出一种面向不规则地块全区域覆盖通用路径规划方法,分析不同障碍物对作业路径的影响并进行系统性的划分整理,针对障碍物不同情况且考虑到农机固有参数限制而规划出相应的局部路径。最后,本文合理选择切换条件,将离线全局路径与实时局部路径相结合形成完整的田间作业路径,并设计开发无人驾驶拖拉机路径规划系统。

1 全局路径规划算法

1.1 地块几何建模

农田地块是拖拉机主要的工作对象,考虑到实际地块环境复杂性,为便于验证算法的正确性,使用 GPS/BDS等导航系统实地测量获取农田地块顶点位置信息，并以E120°为中央子午线进行高斯投影正算，以获得农田顶点的平面坐标[13]。将地块抽象为2D几何多边形后放入平面直角坐标系第一象限中分析,把路径规划问题转换为几何数学问题。若建模时有地块边界垂直于坐标系x轴,应将几何模型旋转一定角度直至无边界垂直于该轴。设n边形地块顶点坐标为(xi,yi)(i=1,2,…,n),其边的大小和方向以向量形式表示。

全局路径需满足连续行驶作业、转弯轨迹应大于拖拉机的最小转弯半径r等条件,因此本文选用梭式法作为拖拉机田间行驶方式,如图1所示。该转弯方式由农机具作业宽度w和r之间的关系确定[14]:w<2r,选用梨形转弯;w=2r,选用半圆形转弯;w>2r,选用弓形转弯。因半圆形转弯可视为弓形转弯特例,本文仅考虑弓形和梨形转弯2种转弯方式。

图1 梭式法全覆盖示意图

1.2 几何地块处理

1.2.1 最佳作业方向求取

全局路径规划重在提高作业效率,使无效路径上的消耗达到最小,因此本节将对最佳作业角ω进行求取,得到最优全局路径。4种评价指标中[15],选取地头消耗最少作为ω求取的指标,即

Ci=TiNi,

(1)

其中:αi为作业直线与第i条边界夹角;Li为第i条边界的长度;Ti为第i条边界上单个转弯消耗时间;Ni第i条边界上转弯次数;Ci为第i条边界上的转弯消耗;C为地头消耗。

设ω∈[0,180°],当αi≠0时,C为连续函数,以作业角θ为变量,θ=0.5°为起始角度,以0.5°为间隔分别计算该角度下的C值,通过选取C最小值,确定ω取值。需注意当αi=0时,在该地块边界无转弯，则C=0。同时,地头消耗求取不考虑整体地块的覆盖,只以各边界为一单位求取对应地头消耗值进行汇总。

1.2.2 几何地块分割

地块建模后,被分为凸形、凹形、复杂多边形地块。由于拖拉机沿ω行驶作业时对某些凹形地块不能一次性遍历,需判断凹形地块是否分割。设过凹点Pi(xi,yi)以ω为倾角做其直线方程y-kωx-b=0,且设与凹点相邻的2个顶点坐标分别为Pi-1(xi-1,yi-1)、Pi+1(xi+1,yi+1)。当(yi-1-kωxi-1-b)(yi+1-kωxi+1-b)>0时,Pi-1、Pi+1两点分布于该直线同侧,需沿最佳作业方向角对凹点进行分割,形成新子地块;反之,两点分布于直线两侧,地块无需分割,如图2所示。

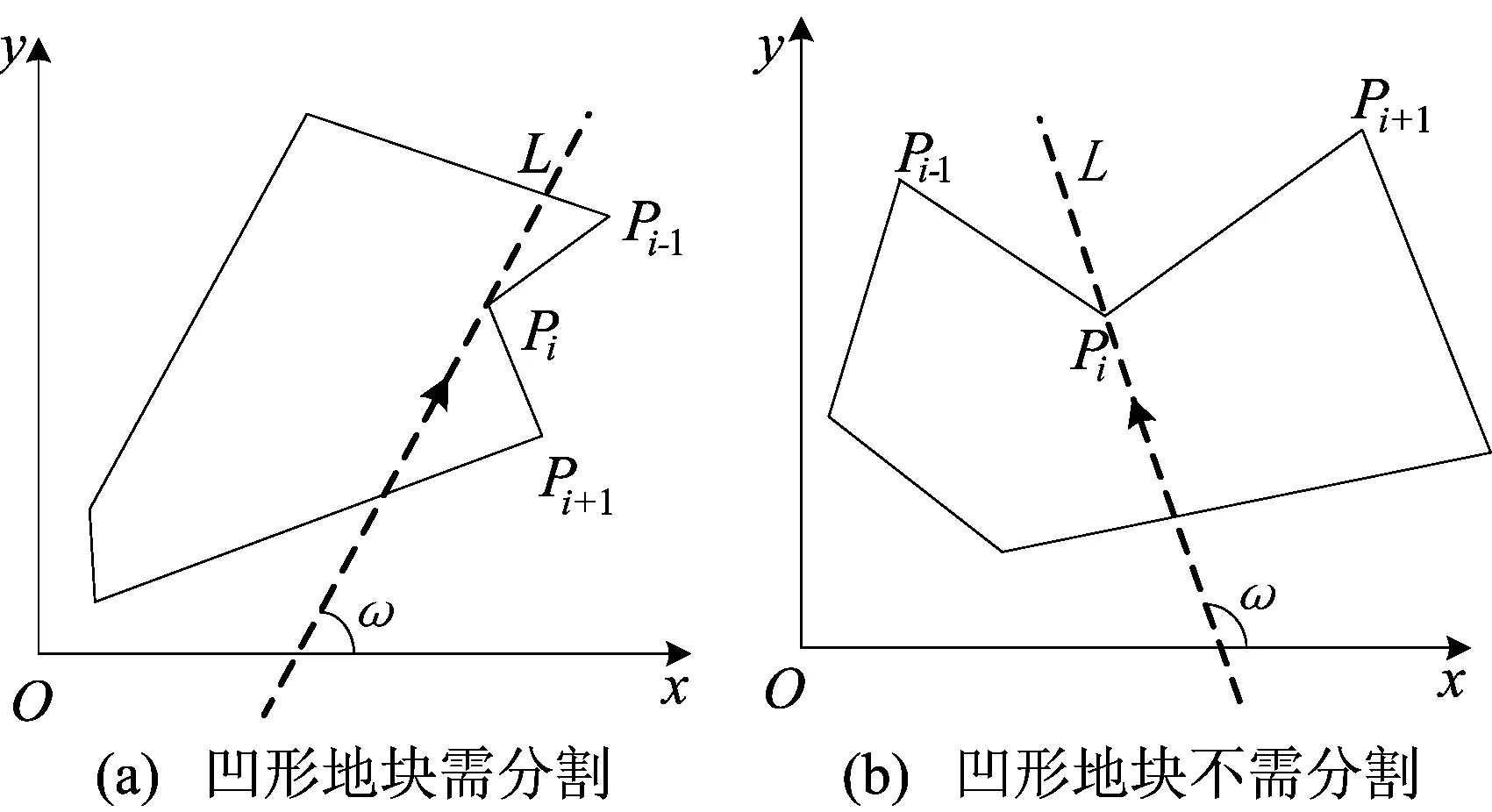
图2 凹点是否需要分割示意图

地块内含障碍物的长或宽大于等于3w时,如存在大沟渠、水坑等,对其采点建模,其在模型中显示为复杂多边形中的“岛屿”或“空洞”。由于大障碍物区域对全局路径规划影响过大,必会增加转弯区域,因此这些转弯区域可被用于子地块之间的路径衔接。以ω为最优分割方向选用“扫线法”对地块进行最优分割,形成若干子地块。需注意,对复杂多边形地块的ω求取应包含地块中大障碍物边界处的地头消耗,以寻求全局最优。当分割出若干子地块时,对各子地块逐个进行路径规划,但子地块的遍历次序也将干扰整体路径作业效率,故本文采用“自上而下、由右到左”的优化次序衔接各子地块,保证整地块的最优全局路径,以复杂多边形地块为例,如图3所示。

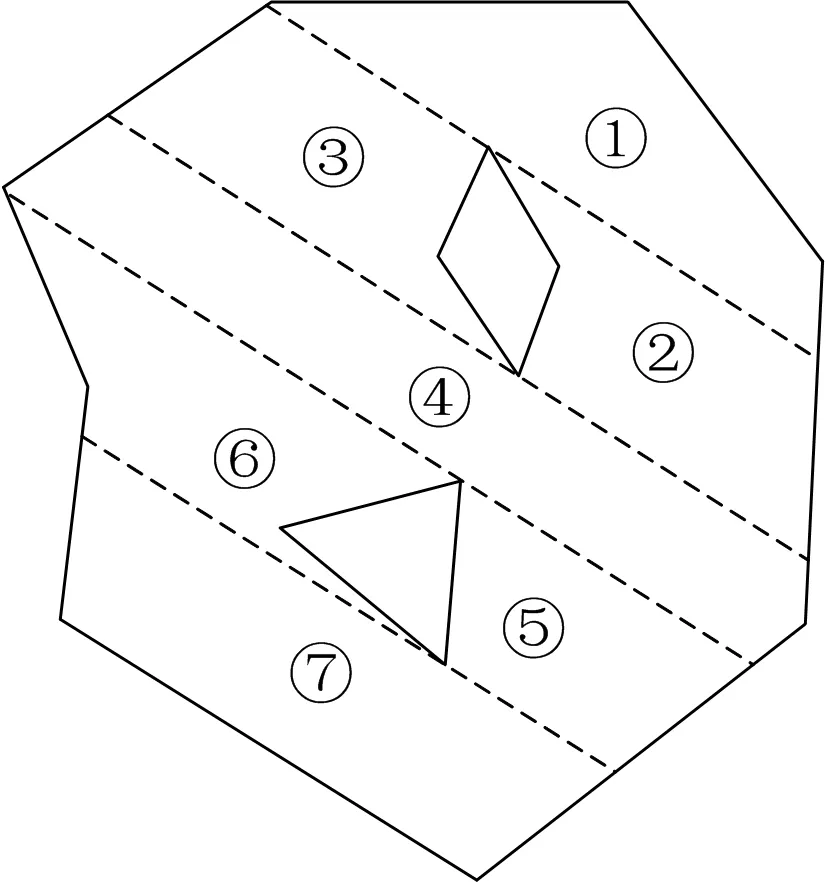
图3 大障碍物地块分割图

1.3 全局作业路径构建

全局路径构建应对3种地块模型分类构建,但后2种地块都可被分割为凸形地块,且不分割凹形地块的路径构建方法与凸形地块一致,因此本文以凸形地块为例,采用几何推理法构建全局路径。

1.3.1 作业区域构建

图4 内缩多边形求解

1.3.2 直线路径构建

为使拖拉机在不规则地块作业时可一次性遍历全地块,且行走方式简单,本文采用“自上而下”的方法进行直线路径构建。

以多边形地块内缩区域A′B′C′D′为例,如图5所示。

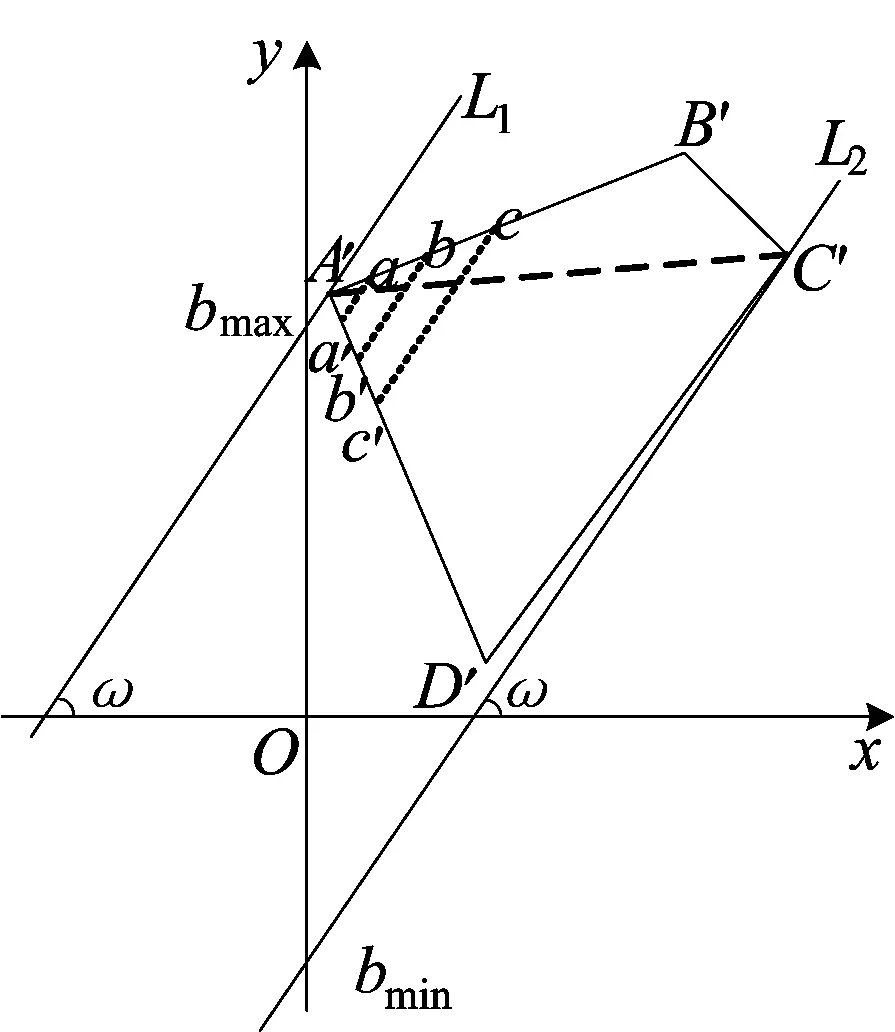
图5 直线路径构建示意图

以ω为倾角,过A′点所对应的直线L1的截距为最大截距bmax,过C′点所对应的直线L2的截距为最小截距bmin,则A′为上方端点,C′为下方端点,连接线段A′C′,A′C′将A′B′C′D′ 分为左、右两侧。A′C′的下方为地块的左侧,上方为地块的右侧。L1以不同w在y轴上投影值为平移量依次向下平移且不超过L2,依次连接左右两点并均分形成完整的直线路径。

自上而下第n行作业行直线方程为:

(2)

其中,bw为w在y轴上投影。

1.3.3 转弯路径构建

拖拉机在地头区域内无论采取何种转弯方式均可被分为4种情形:βi>90°,从地块右侧边界左转或右转;βi<90°,从地块左侧边界左转或右转。以梨形转弯βi>90°右侧转弯为例进行轨迹构建,如图6所示。

图6 βi>90°右侧梨形转弯

(3)

(4)

(5)

(6)

其中:θv为直线P1P4所对应的倾角。

由各圆弧起始角度可知,联合各圆心坐标可以求得各圆弧轨迹点,然后按照遍历次序连接各点即可得到完整的转弯路径,同理可求得其他3种情况的转弯路径。

在直线路径的基础上,按照左右交错、自上而下依次排序的原则将求得的多个转弯路径添加到地头区域,形成完整的全局路径。所规划路径的起点为最上方的直线路径线段与作业区域右侧边界交点,终点则由作业行数的奇偶性决定:若为奇数,最后一条直线路径线段与作业区域右侧边界交点为终点;反之则左侧交点。注意,若起点、终点处的转弯轨迹超出内缩边界,应给予删除。

2 局部路径规划算法

2.1 障碍风险评估

拖拉机沿着全局作业路径在地块内行驶时,其作业区域由远及近可被划分为:障碍物观测区、冲突避让区、紧急避障区。周围作业环境未知,在障碍物观测区内利用感知传感器(激光雷达)不断采集期望路径周边静态障碍物信息。由于激光雷达原始数据是以球坐标系的形式储存,为方便解析处理数据,将激光点球坐标转化为笛卡尔坐标。激光雷达是安装在拖拉机机体上,需将激光坐标系通过平移矩阵和旋转矩阵转换为拖拉机随车坐标系,且随车坐标系是固结于车身上,故需将随车坐标系转化到大地坐标系完成对障碍物绝对坐标系的获取且将其轮廓拟合为最小外接圆形,获得障碍物最小外接圆圆心坐标(x0,y0)和半径R。当静态障碍物半径小于3w,即为小障碍物。

当冲突避让区内有静态障碍物时,需对障碍物进行风险评估。设当前所在直线路径方程为y=kω+b,可求得障碍物圆心与作业路径所在直线的距离d。当R+w/2≤d时为无威胁障碍物,不需要采取任何避障策略,仍沿原作业路径行驶;反之为有威胁障碍物,若拖拉机仍沿原路径行驶,所携带的农机具将会与障碍物发生碰撞,故需进行局部路径规划。

2.2 单障碍物局部路径构建

单障碍物局部作业路径搭建原则是考虑参数限制，使得拖拉机顺利转弯且实现避障后回到原路径上。

(1) 因为拖拉机存在r,且存在w,所以需设定障碍物安全圆区域,保证拖拉机能安全转弯避让障碍物。障碍物最小外接圆半径为R,两者圆心重合。当R≥r-w/2时,其半径RO=R;反之,RO=r-w/2。

(2) 判断安全圆圆心与路径所在直线方程的关系。若kωx+b≥y0,则从上方避过;反之,则从下方避过。

(3) 设拖拉机的前3 s行驶轨迹点为Pi(xi,yi),当前行驶轨迹点Pi+1(xi+1,yi+1)。局部路径规划时可被分为4种情况:当xixi+1,下行上避障或下避障。

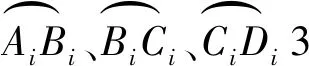
2.3 多障碍物局部路径构建

当拖拉机行驶路径上有多威胁性小障碍物时,沿行驶方向定义为Z1,Z2,…,Zn。首先,不考虑其他障碍物存在,构建各小障碍物避障路径,设各避障路径为Si(i=1,2,…,n),如图7所示。

图7 单/多障碍物避障轨迹示意图

(1)DiAi+1与直线路径线段夹角为0°或长度为0时,拖拉机可从2个障碍物之间安全通过,因此,沿路径Si行驶避过Zi,令i=i+1,对Zi+1采取局部路径规划,直至到检测范围内的Zn。

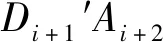
3 路径规划系统软件设计及测试

3.1 路径规划系统软件开发

无人驾驶拖拉机路径规划方法需将全局路径规划方法和局部路径规划方法相结合,使得离线规划的全局路径与实时规划的局部路径相结合形成完整田间作业路径,从而保证路径规划的全局最优性和局部实时性,具体结合流程如图8所示。

3.2 路径规划系统软件测试

基于上述算法,本文使用LabVIEW2016作为开发工具,该系统软件通过BDS采集方式获得试验地块电子地图,可在此软件中规划出最优作业方式的路径规划图,用户可以通过一个友好的界面来完成地块搭建、最佳作业角选取、自主路径规划等功能。支持各种标准化数据格式的作业路径输出,界面如图9所示。

图9 路径规划系统软件前面板

为了检验路径规划算法和系统软件的有效性,设r=5 m,令w为6、12 m,选取地块顶点坐标为(108,257)、(288,205)、(327,85)、(147,17)、(76,18)、(10,85)、(1,180),然后进行全局路径规划。

手动输入期望路径前、后轨迹点和各静态小障碍物坐标Z1(104,227)、Z2(92,199)、Z3(132,185)、Z4(159,196)、Z5(195,171)、Z6(99,99)、Z7(122,109)、Z8(240,140)、Z9(246,145)、Z10(188,80)、Z11(201,84)、Z12(186,52),对应R为3、3、4、3、6、5、5、4、3、3、3、1 m,模拟实时局部路径规划,其结果如图10所示。

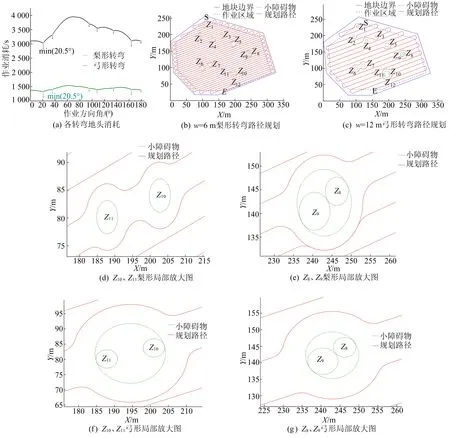
图10 系统软件测试结果1

由图10的全局路径规划结果可知:w=6 m时,选用梨形转弯,其ω=20.5°;w=12 m时,选用弓形转弯,其ω=20.5°,相较于梨形转弯,由于w增加导致地头消耗显著减少。在2种转弯方式下,沿该方向对地块进行路径规划,S为起点,E为终点,其规划的路径末端作业行与地块距离均大于w/2,起点、终点和转弯方式均符合作业要求,且都能满足对地块的全覆盖要求,符合本文设计要求。

由图10的局部路径规划结果可知,因w不同,障碍物风险评估的结果、相邻障碍物的评判标准不同。w=6 m,Z1、Z2、Z3、Z4对多条作业路径都具备威胁性,上下都需进行避障;Z10、Z11相邻但不满足合并条件,因而各视为单一障碍物进行避障路径规划。w=12 m,Z1、Z2、Z3、Z4仅对单一作业路径具备威胁性,只需进行上/下避障;Z10、Z11相邻但避障圆有交点,拖拉机不能从两障碍物之间安全经过,需合成一新障碍物进行避障路径规划,合成的新障碍物圆内切于Z10、Z11两障碍物圆且圆心坐标为(194,82),R=10 m。由于Z8、Z9两障碍物圆相邻过近,无论w数值为多少都需合成一新障碍物进行避障路径规划,其圆心坐标为(243,142),R=7 m,该圆内切于Z8、Z9两障碍物圆。

综上所述,本文所提出的局部路径规划可针对单障碍物、多相邻障碍物进行实时局部路径规划避障,且避障后仍回到原期望路径,符合本文设计要求。

对其余地块以及相应转弯工况类型进行系统测试。

设地块顶点坐标为(43,247)、(184,236)、(236,369)、(391,359)、(347,163)、(18,13),令w=7 m,r=3 m,结果如图11所示。

仍选取上述凸形地块,内设一大障碍物,其顶点坐标为(139,161)、(200,130)、(170,80)、(120,120),w=5 m,r=2.5 m,结果如图12所示。

图12 系统软件测试结果3

由图11可知,初始地块ω=24.5°,由于在该方向作业时不能一次性遍历地块,需沿凹点进行分割,子地块① 的顶点坐标为(43,247)、(184,236)、(384,328)、(347,163)、(18,13),子地块② 的顶点坐标为(236,369)、(391,25)、(384,328)、(184,236),对子地块① 、子地块② 重新进行全局路径规划,两子地块ω均为24.5°,在该方向下对两子地块所规划的路径均符合本文设计要求。

由图12可知,原始地块ω=20.5°,地块建模时为复杂多边形,需沿此角度对地块进行扫线分割,子地块① 的顶点坐标为(108,257)、(270,209)、(7,109)、(1,180),子地块② 的顶点坐标为(270,211)、(288,205)、(170,80)、(200,130)、(139,161),子地块③ 的顶点坐标为(139,161)、(120,120)、(170,80)、(57,38)、(10,85)、(7,109),子地块④ 的顶点坐标为(312,134)、(327,85)、(147,17)、(76,18)、(57,38),对子地块逐个进行全局路径规划。子地块① 、子地块③ 的ω均为21.5°,子地块② 、子地块④ 的ω均为20.5°,在各自最佳作业角下对子地块规划的路径均符合本文设计要求。

4 路径规划实车试验

为验证该系统实用性,本文依托课题组设计的无人驾驶拖拉机实车试验平台进行实车试验,r=5 m,实车平台如图13所示。地块顶点坐标信息可由组合导航测定,其由北斗星通UB842高精定位板卡和驿唐DTU共同组成。采用固定支架将激光雷达安装在拖拉机前配重上,并通过网线与LabVIEW连接,可实时检测获得障碍物雷达坐标,经过雷达坐标与拖拉机随车坐标转换及拖拉机随车坐标与大地坐标转换获得障碍物绝对坐标信息。

试验场地为安徽泗州拖拉机制造有限公司的实车试验场,该场地由多层沥青结构面铺装而成,试验车试验时的挡位为低快3挡,油门开度40%,车辆始终保持10 km/h直线行驶速度,因场地原因未携带农机具,虚设w=5 m,当拖拉机转弯时应自行减速,转弯成功后自行加速回至原速度。

图13 无人驾驶拖拉机实车试验平台

打开LabVIEW软件里的“自主路径规划”选项卡进行作业路径规划:① 采集路径规划的坐标原点,为了避免路径点出现负值,坐标原点需设置在所规划的作业区域的东南方;② 从地块的右上角开始,顺时针采集地块的边界点的坐标信息;③ 设定 “作业速度”、“转弯速度”、“作业幅宽”和“转弯半径”等参数,系统会自主规划出期望作业路径,并将作业路径信息输入给“循迹系统”,进行路径跟踪。

在试验场地中,采集出一不规则地块顶点坐标信息,经处理后的各顶点坐标值为(2 148,2 186)、(2 208,2 258)、(2 249,2 239)、(2 155,2 130)、(2 146,2 131),随后进行全局路径规划。

由于场地过于平坦,人为设置多个相邻小障碍物,如图14a所示。当拖拉机沿该全局路径行驶至障碍物区域进行实时局部路径规划,完整路径规划实验结果如图14b所示。

由图14b可知,所规划的全局路径可实现对地块的全覆盖。当无人驾驶拖拉机沿期望路径自主行驶至小障碍物区域时,进行实时局部路径规划,规划的局部路径可实现对障碍物避障,且避障后仍回到原期望路径上,满足本文设计要求。直线路径跟踪偏差稳定在0.07 m上下波动,转弯时,由于目标路径曲率突变,跟踪偏差会迅速增加,但最大不超过0.23 m,且可迅速被修正。因此本文设计的路径具有较大的实用价值,可以作为无人驾驶拖拉机的参考作业路径,具有一定的现实意义。

图14 路径规划实车试验

5 结 论

(1) 本文综合农田几何形状和作业机具参数等因素设计全局路径规划方法,并在全局路径的基础上针对单个及多个相邻小型静态障碍物实时搭建局部路径;根据切换条件,将离线规划全局路径与实时规划局部路径相结合，形成完整的田间作业路径,保证作业路径的全局最优性和局部实时性。

(2) 基于所述路径规划算法,设计无人驾驶拖拉机路径规划系统,设定参数自主规划,结果表明对于不同形状地块在不同转弯工况下均可以规划出全局路径,并可根据模拟障碍物信息实时规划出局部路径。为验证算法的实用性,基于某型拖拉机搭建实车试验平台,根据作业情况设计试验工况,结果证明本文所设计的算法有较大的实用价值。