带资源约束的异构多核任务复制调度算法

王月恒, 倪 伟, 汪 敏

(合肥工业大学 微电子学院,安徽 合肥 230601)

由于具有高性能、低功耗、易扩展等优点,多核处理器自问世后,迅速成为当前主流的处理器架构[1]。

对于多核处理器,合理的任务调度策略是提高任务并行度、减少任务执行时间的关键因素之一。此外,异构多核处理器中的各处理器核在功能和性能上大多存在差异,因此与同构多核处理器相比,任务调度问题更为复杂,在多项式时间内无法得到最优解,属于NP完全(non-deterministic polynomial complete,NPC)问题。

为了在合理的时间内得到多核处理器并行任务调度问题的近似最优解,学术界针对该问题进行了广泛的研究,提出了多种启发式调度算法。根据算法的特征,可将这些算法分为基于列表的调度算法(HEFT[2]、PEFT[3]、lookahead[4])、智能搜索算法(GA[5],PSO[6],TS[7]、AS[8])以及基于任务复制的调度算法(TDS[9]、MJD[10]、WPTS[11]、TANH[12]、TDCA[13])。其中,基于任务复制的调度算法主要思想是以子任务的冗余计算为代价,减少不同处理器核上的任务间通讯消耗,进而获得更短的调度长度(makespan)。当选用合理的复制策略时,任务复制算法能获得比其他算法较优的调度结果[14]。

TDS算法[9]是经典的基于任务复制的同构多核任务调度算法,采用了基于聚簇与任务复制的策略,其主要思想是将有向无环图(directed acyclic graph,DAG)中join节点与其关键前驱任务分配到同一处理器,以降低并行执行时间。但TDS算法只适用于同构多核系统,且在内核数量不限的情况下,TDS算法不允许join节点的任何2个前驱节点调度到同一个处理器,影响算法调度效果。

文献[13]提出了一种基于任务复制的聚簇算法——TDCA算法。该算法在TANH算法的基础上进行了改进。TDCA算法针对异构系统引入了一种新的参数计算方法,并根据参数对任务节点进行分簇,生成初始任务集群;随后根据任务复制算法的链式反应,采用关键前驱链复制策略优化初始集群,进一步缩短调度长度;最后通过队列合并与任务插入在不增加调度长度的基础上,减小占用的计算单元数目。但TDCA算法仍存在以下不足:

(1) 部分参数的定义未考虑资源约束,过于理想化。在某些算例的调度过程中,尤其针对任务节点前驱任务较多的算例,会出现与实际情况偏差过大的情况,缺少参考价值。

(2) 布局优化阶段的偶然性较强。TDCA算法的队列优化阶段主要包含队列合并与任务插入2个环节。对于TDCA算法的队列合并环节,若布局不更新,每一队列最多仅能尝试进行一次合并操作,操作次数的限制使得部分算例在队列优化阶段后无法得到提升，而任务插入环节对缩短调度长度的作用也十分有限。

针对上述不足,本文提出带资源约束的异构多核系统任务复制调度算法(task-duplication scheduling aglorithm with resource constraints,TDSA-RC)。与TDCA算法相比,该算法主要有以下改进:

(1) 新的参数计算方式。在计算参数时通过限制分配到同一内核上任务的个数,在一定程度上体现了实际系统中资源约束的影响,使得计算出的参数更加精确。

(2) 适用性更强的优化方式。扩大了单一队列操作次数的限制,提高了布局优化阶段的有效率。

(3) 通过冗余筛除及时清除复制阶段引入的对缩短调度长度没有意义的重复节点计算。

1 模型与约束

1.1 任务模型

任务调度问题的通用解决思路是将任务与多核系统抽象成某种形式的模型来设计调度算法,最普遍的方法是采用有向无环图(directed acyclic graph,DAG)模型对待调度的任务进行抽象建模。通过对任务进行抽象建模,便可将复杂的多核任务调度问题转化成特定约束下的DAG调度问题[15]。

在DAG图中将异构多核系统下的任务抽象成一个五元组，即

G=(V,E,P,W,C)

(1)

V={v1,v2,…,vNT}为任务节点集合,NT为集合中任务节点的数量,vi∈V为任务节点集合中的一个子任务。

E为边集,e(i,j)∈E为任务vi到任务vj存在数据通讯。

P={p1,p2,…,pNP}为多核处理器上内核的集合，NP为集合中内核的数量。

W为子任务的执行时间。对于异构多核系统,同一任务在不同内核上的执行时间存在差异,因此往往通过一个NT×NP的任务计算消耗表给出对应的数值。为方便区分,任务vi在内核pk上的执行时间记为w(vi,pk)。

C为任务间的通讯时间,如c(i,j)表示任务vi、vj分配到不同内核时,任务间通讯需要消耗的时间。为衡量DAG中通讯时间与执行时间的关系,引入通信计算比(communication to computation ratio,CCR)表征平均通讯时间与平均执行时间的比值。

若CCR越大,则DAG图中通信占比越高;反之,则表示通信占比越小。

1.2 特殊集合与特殊节点

为方便表述,本节给出某些特殊节点/集合的定义。

如果某个节点存在到任务节点vi的通路,那么该节点即为任务vi的一个前驱任务,vi所有的前驱任务的集合记为PRED(vi);如果某个节点存在来自任务节点vi的通路,那么该节点即为任务vi的一个后继任务,vi所有后继任务的集合记为SUCC(vi)。

布局Sch用于表示调度的队列分配结果,1个完整的布局Sch包含Sch(p1)、Sch(p2)、…、Sch(pNP)共NP个队列,分别对应p1、p2、…、pNP被分配到的任务队列。

没有前驱任务,只有后继任务的任务节点被称为源点(entry-node);没有后继任务,只有前驱任务的任务节点则被称为汇点(exit-node)。

有2个及以上前驱任务的任务节点被称为join节点;有2个及以上后继任务的任务节点则被称为fork节点。

队列节点Sch(pi,k)表示任务队列Sch(pi)中第k个任务节点。

1.3 算法的约束条件

对∀vi∈V,在实际调度中需要考虑2个值st(vi,p)和ct(vi,p),分别代表任务节点vi的在内核p上的开始时刻和完成时刻。当任务进行实际调度时,需满足以下约束条件:

(1) 资源约束。分配到同一个内核上的任务,其执行时间不能重叠,即

(2)

(2) 数据约束。存在数据通讯的2个任务,只有在前一任务完成且将数据结果传递到后一任务所在的内核后,后一任务才能开始,即

ifvi,vj∈Sch(pk),e(vi,vj)∈E

⟹ct(vi,pk)≤st(vj,pk)或

ct(vj,pk)≤st(vi,pk)

(3)

(3) 任务约束。子任务是原子性的,执行过程不可中断,由此可以得到:

ct(vi,pk)=st(vi,pk)+w(vi,pk)

(4)

2 算法流程

2.1 参数计算

关键路径是DAG任务图的最长路径,是算法压缩调度长度的瓶颈所在。在调度算法中,关键路径的确定与优化十分重要。而对于异构多核处理器,由于任务在不同内核上的执行时间存在差异,确定关键路径时一方面需要考虑各个任务间的通讯消耗,另一方面还需要考虑在实际调度过程中任务的分配情况。因此,异构多核系统下的调度算法在实际调度前无法准确定位关键路径,借助参数估算关键路径是异构多核调度算法的常见方法。

定义1 任务vi在内核pk上的最早开始时刻为est(vi,pk)。在TDCA算法和TDSA-RC算法中,est(vi,pk)都是一个理想值,不用考虑计算单元是否被占用。TDCA算法中est(vi,pk)的计算公式如(6)式所示,其含义为在所有前驱任务vj调度到最理想内核的情况下,最后一个前驱任务到达pk的时刻即为任务vi在pk最早开始时间，该值是不考虑内核资源约束的理想值。

所有前驱任务vj都调度到最理想内核这一条件在实际调度过程中是很难实现的。例如,调度到当前内核pk不需要计算通讯消耗,使得pk被大多数前驱任务认定为最理想内核的概率增高。若前驱任务堆积在pk上,则会使因没有考虑内核资源约束而造成的误差大大增加,从而降低参数的可信度。

本文提出了一种新的参数计算方式,在一定程度上考虑调度过程中pk的资源约束问题。在计算est(vi,pk)时补充条件:vi的前驱任务中,有且仅有一个任务被放置在pk上。当确定了某个前驱任务vm调度到pk后,其余的前驱任务只能被调度在除pk以外的次优内核,并补充通讯消耗,由此得到:

(5)

其中

(6)

(7)

ect(vk,fproc(vk,1))+comm(vk,vi,fproc(vk,1),fproc(vi,1))}

(8)

定义2 任务vi在计算单元pk上的最早完成时刻ect(vi,pk)。根据(4)式所描述的任务的原子性约束,在得到最早开始时刻的计算结果后,就可以计算出任务vi在计算单元pk上的最早完成时刻ect(vi,pk)。

ect(vi,pk)=est(vi,pk)+w(vi,pk)

(9)

定义3 任务vi对内核的优先级。根据任务vi在不同内核的最早完成时刻ect(vi,p),按照非降序的原则对内核进行排序,得到任务vi对内核的优先级列表fproc(vi)。其中,优先级最高的内核被记为fproc(vi,1),意味着根据估算当vi调度到pk时拥有最早结束时刻。因此,可以根据优先级得到以下推断:

ect(vi,fproc(vi,1))≤ect(vi,fproc(vi,2))≤

…≤ect(vi,fproc(vi,NP))

(10)

定义4 关键前驱任务cpred(vi)。关键前驱任务是最晚到达当前内核的前驱任务,是优化当前任务最早开始时刻的瓶颈。TDSA-RC算法中关键前驱任务的定义如(8)式。

定义5 任务优先级。为避免调度过程中发生数据冲突而造成算法中止,在生成初始布局前需要对任务节点进行排序。TDSA-RC采用权值b-level(vi)确定各任务的优先级。权值b-level(vi)的计算方法如(11)式所示,该权值代表了当前子任务节点到达汇点的最长路径长度。按照b-level(vi)递减的原则对任务节点进行排序,可得到任务优先级列表(task priority list,TPL)。

(11)

定义6 关键前驱链。对于任意任务vi,其关键前驱链被定义为cpred(vi),cpred(cpred(vi)),……,直至追溯到源点。

2.2 生成初始布局

完成参数计算后进入生成初始布局的阶段。

从优先级列表TPL中的第1个任务vk开始,将其分配到fproc(vk,1),然后依次补充当前节点的关键前驱任务,直至调度到源点。

随后从剩余未调度的节点中,选择b-level值最大的任务节点vp作为当前任务curtask,进行第2次分配,将其调度到空闲且当前内核优先级最高的内核队列,然后对其关键前驱任务进行调度。若其关键前驱任务cpred(vp)在第1次调度时已被调度到其他内核队列,则从vp的前驱任务中,选择ect(vt,curtask)最小且未被调度的任务节点vt,将vt调度到当前内核队列。以此类推,直至所有任务节点都完成调度。在生成初始布局时需要注意以下几点:

(1) 若curtask有且只有一个前驱任务,则直接将该唯一的前驱任务添加进当前内核队列。

(2) 若curtask存在多个前驱任务,则首先检查curtask的关键前驱任务vi=cpred(curtask)是否满足添加条件,即判断是否满足不等式ect(vi,fproc(vi,1))+c(vi,curtask)≥ect(vi,curtask),vi∈PRED(curtask)，目的是检查当任务调度vi被调度到其最佳队列Sch(fproc(vi,1))时,能否得到比调度到当前队列更早的到达时间。若满足添加条件,则将vi添加进curtask所在队列;若不满足添加条件,则寻找其他前驱任务代替cpred(curtask);若找不到合适的替代任务,则中断该队列的生成过程,进行新队列的生成。

生成初始布局的伪代码如下:

for (task:TPL[1] to TPL[NP])

curtask=first unassigned task in TPL;

curproc=first proc in fproc(curtask)

&Sch(curproc)={ø};

Sch(curproc)=Sch(curproc) ∪{curtask};

while curtask≠entry-node do

ptask=cpred(curtask);

if [in-degree(curtask)>1 &

(ptask is assigned or

ect(ptask,fproc(ptask,1))+

c(ptask,curtask)

Find unassigned ktask:

1.ktask∈PRED(curtask)

2.ect(ktask,fproc(ktask,1))+

c(ktask,curtask)≥ect(ktask,curproc)

3.minimizes ect(ktask,curproc);

if (ktask not exits)

back to line1;

else

ptask=ktask;

endif

Sch(curproc)=Sch(curproc)∪{ptask};

curtask=ptask;

end while

end for

2.3 任务复制

在任务复制阶段,采用链式复制策略,主要分为如下2个步骤。

(1) 寻找符合条件的备选点。备选点只需要满足以下2个条件中的一个即可:①备选点是队列头节点Sch(p,1),但不是源点;②备选点Sch(p,x)的前一节点Sch(p,x-1)不是Sch(p,x)的关键前驱任务。

(2) 针对备选点进行任务复制。对于满足条件①的备选点,直接将备选点的关键前驱链复制到当前任务队列;对于满足条件②的备选点,将备选点前的任务移动到空闲且对Sch(p,x-1)而言优先级最高的内核队列上;若此时不存在空队列,则直接移动到fproc(sch(p,x-1),1)。最后,将备选点的关键前驱链补充进当前队列。

完成任务复制操作后,需要进一步判定调度长度是否得到优化:若长度减少,则保留复制后的布局;否则恢复原有布局。

任务复制的伪代码如下:

for (times:1 to TD-times-para)

for (curproc:1 to NP)

for(Sch(curproc,x):Sch(curproc,1) to Sch(curproc,last))

Sch-copy←Sch;//back-up

if(Sch(curproc,x-1)≠

cpred(Sch(curproc,x)))

nextProc=first processor in

fproc(Sch(curproc,x-1),1) to

fproc(Sch(curproc,x-1),NP)

&Sch(nextProc)={ø};

if(nextProc not exits)

nextProc=fproc(Sch(curproc,x-1),1);

endif

move Sch(curproc,1)、

Sch(curproc,2)、…、Sch(curproc,x-1) to

Sch(nextProc);

Add predecessor trail of

Sch(curproc,x) to Sch(curproc);

else if(Sch(curproc,1)≠entry-node)

Add predecessor trail of

Sch(curproc,1) to Sch(curproc);

else

If (makespan(Sch)>makespan(copy-Sch))

Sch←copy-Sch;

end if

end for

end for

end for

2.4 布局优化

任务复制完成后进行布局优化,优化过程分为2个环节,一是针对join节点的队列合并;二是冗余节点筛除。

TDCA算法的布局优化是通过将队列与该队末任务的最佳内核队列合并,其优化效果的实质是通过将不在同队列的join节点前驱,合并到同一队列实现的,而TDSA-RC扩大了队列合并的适用范围,并结合删除冗余节点对布局进行优化。布局优化的伪代码如下:

Sch←after-tp-sch

for (times:1 to op-times-para)

for (cproc:p1topNP)

for (ctask:Sch(cproc,1) to

Sch(cproc,last))

if [ctask is join node &&

∀v∈Sch(pv),v∈PRED(ctask),

pv≠cproc]

Sch-copy←Sch;

Add predecessor trail ofvandvto Sch(cproc);

if [makespan(Sch)≤makespan(Sch-copy)]

Sch←Check-Redundance(Sch)

endif

else Sch←Sch-copy;

endif

end for

end for

end for

final-Sch←Sch;

删除冗余节点的目的是检查任务复制过程中是否向布局内引入对改进调度长度无意义的冗余计算,若存在,则将其删除。冗余节点筛除的伪代码如下:

for(cproc:p1topNP)

for(ctask:Sch(cproc,1) to

Sch(cproc,last))

If(∃ctask∈Sch(p),p≠cproc)

Sch-copy←Sch;

delete ctask in Sch(cproc);

if[makespan(Sch)>

makespan(Sch-copy)]

Sch←Sch-copy;

endif

end for

end for

After-check-sch←Sch;

3 实 验

3.1 实验概述

为了验证所提TDSA-RC算法的调度效果,采用C语言分别实现了TDCA、HEFT、PEFT和TDSA-RC 4种算法。实验主要分为如下2个部分:

(1) 验证TDSA-RC算法处理任意随机的任务图时的加速效果。

(2) 验证TDSA-RC算法在处理实际任务图时的加速效果。

3.2 随机任务图实验

参考文献[13]中生成随机任务图的流程,本实验选取任务图中任务节点的总数(NT)、异构处理单元的总数(NP)、随机任务DAG的最大层级数(LEVEL)、通讯计算比(CCR)、系统异构程度(OFFSET)和任务通讯所能跨越的最大层级数(CROSS-LEVEL)作为生成随机任务图时的参数。针对每一类型的变量生成了25张任务图,总计生成51 200张任务图。各个参数的取值范围与默认值见表1所列。

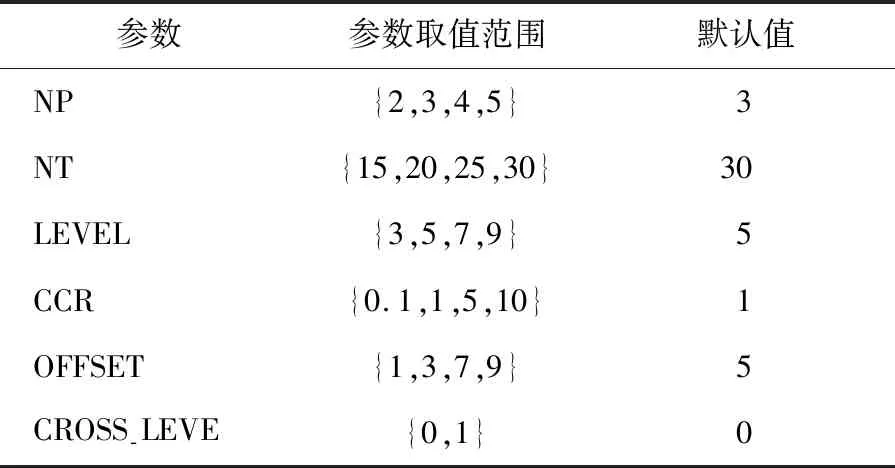
表1 随机DAG参数及取值范围

算例生成程序在生成异构多核平台的计算消耗表时,首先生成NP个中心值mid(v),其取值范围为[MMIN,MMAX]。mid(v)为计算消耗w(v,p)的取值范围中心,w(v,p)∈[mid(v)-OFFSET,mid(v)+OFFSET],OFFSET越高则系统异构程度越强。实验中MMIN、MMAX的默认值分别为10、20。CROSS-LEVEL代表任务通讯所跨越的最大层级数。

在生成的51 200张随机任务图中,将TDSA-RC算法与TDCA、PEFT和HEFT算法的调度结果进行对比,取得更优、更差以及相同调度长度的概率统计结果见表2所列。

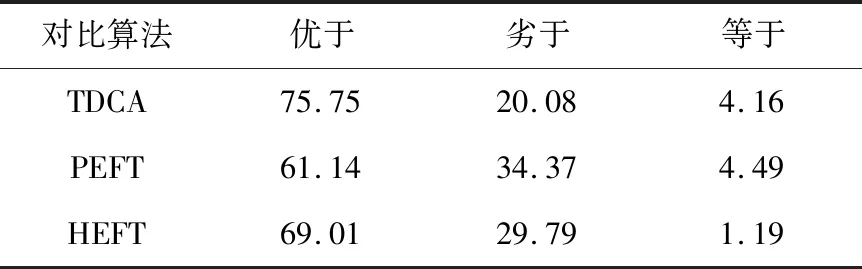
表2 随机任务图调度结果概率统计 %

由表2可知,若多核系统需要处理多种类型的随机任务,相比TDCA、PEFT和HEFT算法,采用TDSA-RC算法进行调度获得更好的结果几率更大,其中与TDCA算法对比时,TDSA-RC算法的优势最为明显。

实验还进一步地验证了TDSA-RC在不同的参数取值下相比于TDCA算法的加速效果。TDSA-RC相对TDCA在处理随机任务图时的平均加速效果以ACC(TDSA-RC,TDCA)表示,简记为ACC,其计算公式如下：

ACC(TDSA-RC,TDCA)=

100%

(12)

2种算法在不同参数取值下的相对加速效果变化如图1所示。

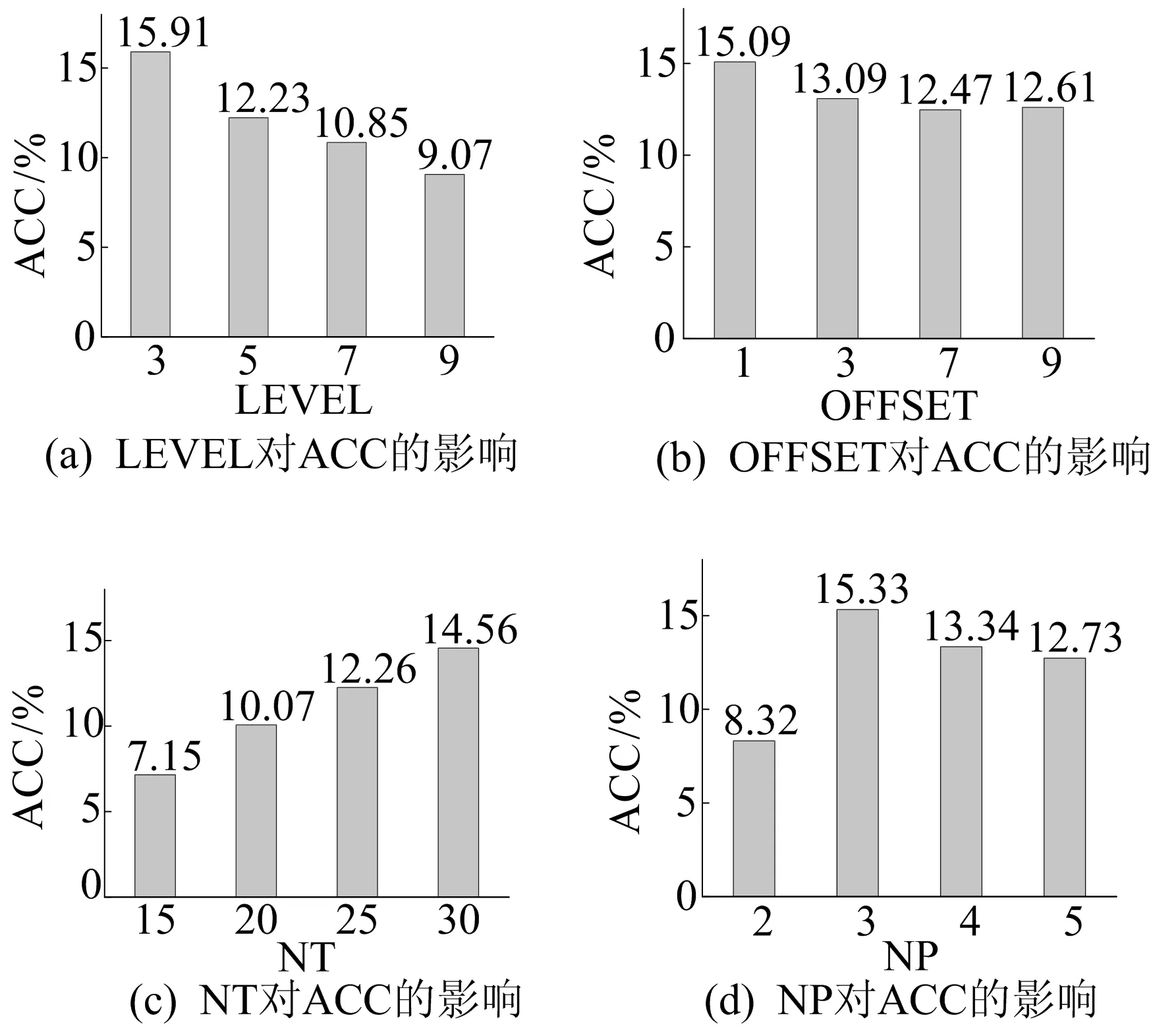
图1 随机任务图实验结果

由图1a～图1e可知,在选定参数的范围内,无论LEVEL、OFFSET、NT、NP、CCR如何变化,TDSA-RC算法都能取得较好的效果,平均加速比为12.08%；当LEVEL=3或NT=30时,平均加速比可达15%以上。此外,由图1a、图1c可知,ACC的数值与DAG的任务节点总数NT成正相关,而与DAG的任务层级数LEVEL成负相关。因此,与TDCA相比,TDSA-RC更适合处理规模较大、层级数较小的任务图,而参数OFFSET、CCR的取值对ACC影响不大。

3.3 实际任务图实验

本实验验证TDSA-RC算法相比于TDCA算法在处理实际任务时的相对加速效果。实验采用的DAG结构如图2所示。

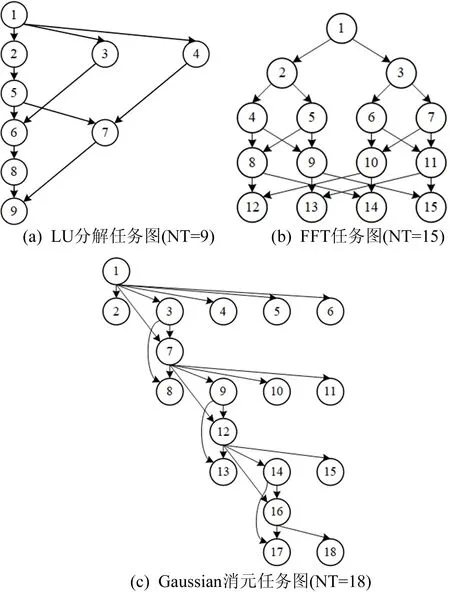
图2 实际任务的DAG

图2中，LU分解(记为LU)、快速傅里叶变换(fast Fourier transform,FFT)、高斯(Gauss)消元以及相同节点数的随机(Random)3种常见任务[16]作为调度对象进行对比。

图2中各个任务节点的计算消耗、通讯消耗由算例生成程序根据参数随机给出,其中非自变量参数MMIN、MMAX的默认值分别为10、20。

实验选取了CCR、NP、OFFSET作为自变量,自变量参数的取值范围与默认值见表3所列。不同参数下相对于TDCA的加速效果如图3所示。

表3 实际任务图参数及取值范围

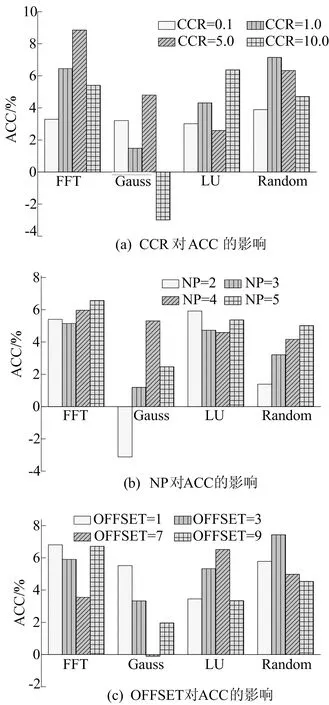
图3 实际任务图实验结果

从图3可以看出,TDSA-RC在对FFT、LU分解进行调度时,其调度结果优于TDCA算法。其中针对FFT的改进最为明显,在多数情况下优于对同等结点数的随机任务进行调度的效果。针对高斯消元的调度效果最差,在某些参数条件下会得到比TDCA算法更差的调度结果。

3.4 时间复杂度分析

TDCA算法的时间复杂度是O(mne+m2e)。其中:n为任务数；m为内核数量；e为通讯数量。

TDSA-RC算法在参数计算阶段的计算参数est(vi,pk)时间复杂度为O(mne),计算ect(vi,pk)的时间复杂度为O(mn)。且因计算内核优先级需要对内核进行排序,TDSA-RC算法中采用的排序算法的时间复杂度为O(m2),计算内核优先级的时间复杂度为O(m2n),计算关键前驱cpred(v)和b-level(v)权值的时间复杂度均为O(ne),因此参数计算环节的总时间复杂度为O(mne+mn+m2+m2n+ne)=O(m2n+mne);生成初始布局的时间复杂度为O(n2+mn+me);任务复制阶段的的时间复杂度为O(mne);布局优化阶段的时间复杂度为O(mn×me)=O(m2ne)。

综上可得TDSA-RC算法的时间复杂度为O(m2ne+n2),可以看出TDSA-RC的调度效果提升是以牺牲时间复杂度为代价的。

4 结 论

针对现有TDCA算法的不足,本文提出了一种异构多核系统任务复制调度算法TDSA-RC。通过在参数计算阶段考虑核的计算资源、改进布局优化方法和筛除冗余节点等方法对任务调度进行优化。通过随机任务图以及以LU分解、FFT和高斯消元为调度对象的对比实验,表明该算法能有效缩短并行任务的调度长度,与TDCA算法相比平均性能提升可达12.08%,更加适合处理规模大、层级少且join节点占比多的并行任务。