基于成霜驱动势冷板霜层生长的数值研究

李晓萍, 刘向农, 孙东方, 刘如佳, 董 婷

(合肥工业大学 汽车与交通工程学院,安徽 合肥 230009)

0 引 言

空气源热泵已经广泛应用在生活中,但是当冬季蒸发器表面温度低于0 ℃且低于空气的露点温度时,换热器表面就会结霜。结霜会造成换热器热阻增加,从而导致换热器的性能下降。因此研究结霜机理对于换热器的结构设计以及除霜具有一定的价值。

结霜过程不仅仅是一个相变过程,更是一个复杂的传热传质过程。文献[1]根据霜层生长初期与树枝生长的相似性,基于有限扩散聚集(diffusion-limited aggregation,DLA)模型建立结霜分形模型,并利用该模型模拟空气流速、冷表面接触角对结霜的影响,但并未引入表面粗糙度对结霜的影响;文献[2]基于DLA模型,在MATLAB平台上建立霜层生长分形模型,模拟深冷表面霜层初期生长过程,但是并未讨论霜层导热系数随时间的变化。随着计算流体动力学(computational fluid dynamics,CFD)的发展,一些学者利用CFD来模拟霜层生长。文献[3]利用Fluent建立霜层生长模型,基于经典成核理论将霜层生长分为冰晶成核和冰晶生长2个部分,建立水蒸气向冰相的质量传递速率模型,这为模拟霜层的生长过程提供了另外一种方法;文献[4]也利用Fluent模拟霜层的生长,从饱和水蒸气浓度与其同温度下的水蒸气浓度差是霜层生长驱动力的角度出发,建立了霜层生长速率的关系式,但是霜面水蒸气采用饱和水蒸气;文献[5]提出霜面上水蒸气应处于过饱和状态,通过与实验数据的对比发现,霜面水蒸气过饱和模型优于霜面水蒸气饱和模型;文献[6]指出,若霜面上湿空气是饱和状态,则传质速率会被高估,并提出了霜面水蒸气过饱和度方程;文献[7]指出,水蒸气浓度差在结霜过程中占主导地位,利用CFD模拟结霜可以消除关于初始结霜厚度和密度的2个假设,同时还可以获得霜导热系数和湿空气绝对湿度的分布。还有学者对结霜进行了实验研究,提出了霜层生长速率的经验关联式。文献[8]进行了霜层的实验研究,对影响结霜的因素进行分析,提出了霜层生长的关联式;文献[9]针对水平冷板上霜层的生长过程,提出霜层密度的半经验关联式。但这些关联式有一定的局限性。

虽然目前已经有大量关于结霜的研究,但是基于霜-气界面水蒸气处于过饱和状态使用CFD模型对结霜形态的研究很少。CFD既可以用来获得霜的形态、生长速率和霜物性参数,也可以用于结构复杂的换热器表面结霜的研究,以补充不同工况下结霜的实验数据。

本文以霜-气界面上过饱和水蒸气与霜域内水蒸气浓度差为结霜驱动势建立相变率表达式,将相变率表达式导入到Fluent中,并耦合欧拉两相流模型建立质量传递模型以研究水平冷板霜层生长与密实化过程。

1 物理模型

霜层生长的物理模型如图1所示。数值模拟区域长75 mm,宽10 mm,湿空气进口参数和低温冷板温度见表1所列。

在计算区域内,霜层的形态是时刻变化的,为了便于观察不同时刻下霜层的形态,引入霜-气界面将计算域划分为湿空气域和霜域,采用冰晶体积分数作为阈值监测霜-气界面的更替变化。湿空气域内冰晶体积分数为0;霜区域内冰晶体积分数小于临界冰晶体积分数,取10-6[3];霜气界面上为临界冰晶体积分数。

结霜是一个复杂的传热传质过程,因此在计算过程中需要一些假设来简化计算:将湿空气视为不可压缩的理想流体;铝板温度低,湿空气直接凝固为冰;在结霜过程中忽略融化和升华。

表1 初始参数

2 霜层生长与致密化模型

在计算区域内,霜-气界面的水蒸气处于过饱和状态,这与霜域内的水蒸气形成浓度差,结霜驱动势形成,冷板上产生冰晶。随着时间的增长,一部分湿空气会增加霜层的厚度,另一部分湿空气会增加霜的密实度。本文将重点讨论霜厚度生长和密度生长规律。

本文采用Fluent中的欧拉两相流模型。在模型中设置两相物质,第1相为连续湿空气(干空气和水蒸气),第2相为冰。将湿空气-霜的相变率表达式以udf形式编程到Fluent中来实现两相之间的质量传递。

2.1 质量传递模型

霜的形成需要经过冰晶成核、生长、塌陷回融等过程。冰晶始于冰晶核,随着晶体生长条件的不同,晶体的形核可以分为均质成核或者异质成核。根据晶体成核理论,相变驱动势主要与饱和水蒸气压力及其水蒸气分压力相关，冷凝驱动势为同一温度下水蒸气浓度与饱和水蒸气浓度之差。湿空气冷凝为水的相变速率[10]如下：

(1)

其中:mwa为湿空气与水之间的冷凝相变率,单位kg/(m2·s);ρa为湿空气的密度,单位kg/m2;D为水蒸气扩散率,单位m2/s;δ为单元网格中心至壁面的距离,单位m;Cphase为相变系数[11];ωsat为水蒸气饱和质量分数;ωwapor为水蒸气质量分数。

霜气界面上水蒸气会越过饱和达到过饱和状态,霜面上过饱和水蒸气与霜域内水蒸气形成浓度差,霜域内不同位置处的浓度差导致了霜的不均匀分布。从结霜驱动势ωsup-ωwapor角度出发修正冷凝相变速率,湿空气中的水蒸气以一定的扩散率进行质量传递,则单位时间内由湿空气相向冰相的质量转移速率为:

(2)

(3)

其中:mia为湿空气与冰之间的相变率;Cphase为相变系数,取106;ωsat为水蒸气饱和质量分数;ωsup为霜面上水蒸气质量分数;τ为修正系数,取0.1。

过饱和度的定义如下：

(4)

文献[6]通过对实验数据分析,得到霜表面过饱和度的经验式，即

(5)

本文使用的工况满足该经验式。在霜-气界面上满足S=Sfs,获得霜面上的水蒸气压力，即

(6)

其中:Pv为水蒸气分压力;Pvs为饱和水蒸气分压力;Sfs为霜气界面上湿空气过饱和度;Pv,∞为来流水蒸气分压力;Pvs,∞为来流饱和水蒸气分压力;Pvs,fs为霜面饱和水蒸气分压力。

由水蒸气压力和理想气体状态方程确定水蒸气的密度,进而确定水蒸气的湿度,最后将湿度转变为水蒸气的质量分数代入(2)式,便可计算湿空气转换为冰的相变率。

2.2 初始条件及边界条件

开始时,计算域充满了湿空气,湿空气的体积分数为1,冰相的体积分数为0,湿空气密度设为不可压缩理想气体,定压比热容、热导率、黏度均按照混合定律设置,水蒸气的扩散率通过编程导入到Fluent中。其他物性参数均为软件默认值。

湿空气入口为速度边界条件,出口为压力边界条件,冷板为恒温边界条件,上壁面为绝热边界条件。

3 结果与讨论

3.1 模型验证

霜层平均厚度和霜质量是衡量霜层生长的重要指标,将其模拟数据与实验数据进行对比,完成本模型的验证。模拟工况选取2种工况,模拟阶段选取20～60 min,对比结果如图2所示,所用的实验数据均参考文献[12]。

在模拟过程中,采用霜-气界面的位置变化来追踪霜层的增长,可以得到在不同时刻霜层的平均厚度,计算公式如下:

(7)

霜层质量的计算公式如下:

(8)

其中：j为湿空气流动方向上的单元网格数;N为湿空气流动方向上全部网格数;L为冷板长度,单位m;Δx为单元网格的长度,单位m;y(t)为霜面上网格纵坐标,单位m;k为霜层高度方向冷板至霜界面之间的网格数;ρi为冰晶密度,单位kg/m2;A为每个单元网格的面积,单位m2;B为铝板的宽度,单位m;S为霜区域的面积,单位m2。

实验中提取t=60 min时霜的质量。在工况为ua=0.92 m/s、Ta=275 K、RH=85%、Tw=265 K条件下霜质量为0.302 g,模拟得到的霜质量为0.259 g;在工况为ua=0.92 m/s,Ta=275 K、RH=85%、Tw=260 K条件下霜质量为0.412 g,模拟得到的霜质量为0.404 g；2种工况下,误差均在15%以内。由图2可知，霜层平均厚度模拟与实验结果的误差均在30%以内，说明该模型可以有效预测结霜特征,可用于后续分析。

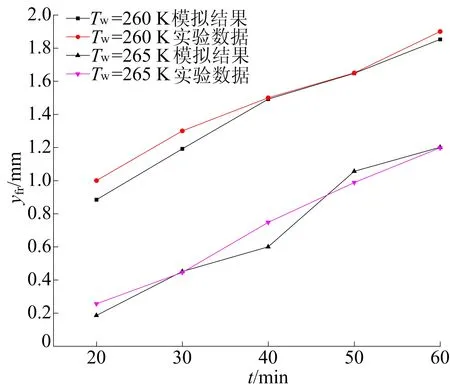
图2 霜层平均厚度模拟结果和实验结果对比

3.2 湿空气温度分布

霜的存在增加了湿空气与冷板之间的热阻,湿空气温度的分布制约着霜层形态。在t=2 h时不同截面上湿空气温度分布如图3所示。霜-气界面将计算域分为湿空气域和霜域,传热方式不同导致2个区域内温度变化速率的不同。

冷板前沿结霜驱动势最大,故冷板前沿霜密集度较大,而霜的导热系数是霜密度的函数,因此冷板前沿温度变化较大。

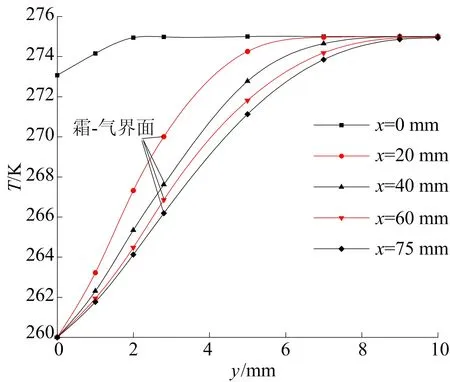
图3 t=2 h时不同截面上湿空气温度分布

在冷板截面x=20 mm上不同时间的湿空气温度分布如图4所示。从图4可以看出,随着时间增加,霜气界面上湿空气温度升高,这会引起界面上过饱和水蒸气质量分数降低,结霜驱动势下降,最终导致霜层形态发生改变,霜层在后期增长缓慢。

抗菌药说明书［适应症］不符合抗菌药说明书撰写技术指导原则的主要表现有：适应症没有按照“本品适用于治疗由对本品敏感的XXX、XXX和XXX菌引起的YYY病。”的规范描述；没有遵循“如果获得的证据仅仅支持用于较大人群的亚群（例如，疾病轻微的患者或特殊年龄组的患者）应予说明”的规定；没有遵循“在某些情况下有理由限制适应症，例如，建议药品不作为某种感染的一线治疗”应予描述的规定；遗漏使用限制的内容。

图4 x=20 mm截面上湿空气温度分布

3.3 霜层形态

霜层形态反映霜的时间和空间特性。霜-气界面上冰晶体积分数的变化率反映霜厚度增长速率;霜域内冰晶体积分数增长速度反映霜密实度增长速率。因此冰晶体积分数是表征霜层形态的重要指标。

冷板不同位置冰晶体积分数的变化如图5所示，选取了距冷板0.1 mm,并且冷板截面在10、20、30、40、50、60、70 mm的7个位置。从图5可以看出：冷板前端冰晶体积分数较大；在2 h之内,冰晶体积分数增长缓慢；在冷板截面10 mm位置处,冰晶体积分数在2～2.5 h内从0.086 32增长到0.150 40,增加了74.2%,此阶段冰晶体积分数增长迅速。

图5 冷板不同位置冰晶体积分数随时间的变化

水蒸气浓度差在结霜过程中占据主导地位。较高的温差和较大的水蒸气浓度差均有利于霜层生长。冷板前沿霜层较厚,霜层较密集,这一现象与结霜驱动势有关,如图5所示,冰晶体积分数在冷板截面20～30 mm之间下降较快,这是因为结霜驱动势在此阶段内减小速率最大。

2.5 h冷板不同位置结霜驱动势的变化如图6所示。从图6可以看出,t=2.5 h时霜气界面过饱和水蒸气的质量分数以及在距冷板高度0.1 mm各截面的水蒸气质量分数在截面10 mm处水蒸气浓度差最大,霜层较厚,霜层较密；之后水蒸气浓度差开始下降,且在截面20～25 mm之间浓度差下降15.6%,下降幅度最大,从而导致截面20～30 mm之间冰晶体积分数差异较大。

图6 t=2.5 h冷板不同位置处结霜驱动势的变化

3.4 霜物性参数

在不同的温度和过饱和度区域内,霜的构造不同,霜的密度和导热系数也不同。文献[13]、文献[14]结合实验数据分别提出了在霜密度小于500 kg/m3霜层导热系数的实验关联式。这种实验关联式更加贴近实际情况。本文采用文献[13]关联式计算霜层导热系数。霜是由湿空气和冰组成的多孔物质,采用加权平均方法计算可得:

ρfr=ρiαi+ρa(1-αi)

(9)

(10)

随着霜面上水蒸气过饱和度的下降,霜域内传质速率大于霜面上传质速率,水蒸气主要扩散在霜层内部,孔隙率下降,霜的密度增长加快。

霜层密度和导热系数随时间的变化如图7所示。在t=2 h以内密度增长缓慢,在t为2～3 h之间霜密度增长速度加快,从58.8 kg/m3增长到116.08 kg/m3,导热系数增加了92.4%。这符合霜导热系数与霜结构形态有关的理论,如图5所示,霜密度分布与冰晶体积分数分布类似,因此冰晶体积分数是影响霜密度和导热系数的重要因素。

图7 不同时刻下霜密度和导热系数

4 结 论

本文基于结霜驱动力建立了湿空气转变为霜的相变率表达式,数值模拟了水平冷板上霜生长与致密化过程；将霜层的平均厚度和霜层质量模拟数据与实验数据进行对比,验证该模型的合理性。用该模型分析了霜层形态和霜物性参数的变化,得到以下主要结论:

(1) 将霜层平均厚度、霜质量模拟数据与实验数据对比,霜层平均厚度误差在30%内,霜层质量误差在15%内,验证了本文模型的可靠性。

(2) 冷板不同截面上均存在霜-气界面点,该界面将计算域分为湿空气域和霜域,2个区域内传热方式不同。随着时间的增加,霜-气界面上湿空气温度升高,这会引起界面上过饱和水蒸气质量分数降低,从而导致结霜驱动势下降,霜层形态发生改变。

(3) 结霜初期,霜面上传质速率处于主导地位,达到时间临界点后,霜域内传质速率大于霜面上传质速率，这决定了结霜初期水蒸气主要用来增加霜层厚度,后期水蒸气主要用来增加霜的密度。霜密度与冰晶体积分数分布类似,因此冰晶体积分数是影响霜密度和导热系数的重要因素。

本文主要工作是提出霜层生长与密实化数学模型,使用冷板结霜验证模型的合理性,并利用该模型分析结霜机理,为换热器结霜和除霜研究提供一定的理论基础。