知识整体建构 素养有效提升——六年级“图形的运动（练习）”教学实践与思考

□ 杨兴谱 顾志能

【课前之思】

现行各套小学数学教材关于“轴对称”知识的编排，均未能很好地揭示轴对称是图形的运动。例如，人教版教材虽然两次编排了轴对称相关的知识（二年级下册的“轴对称图形”和四年级下册的“轴对称”），但并不能使学生很好地体会轴对称是图形的运动。在学生的意识中，轴对称就是轴对称图形的简称，或者说是描述图形特征的一个名词。

这种模糊的认识，让学生到了六年级总复习阶段梳理图形的运动相关知识时面临麻烦。人教版教材六年级下册总复习时编排了这样一道题：我们学过哪些关于图形的运动的知识？哪些运动不改变图形的形状和大小？哪些运动只改变图形的大小，而不改变形状？还设计了相关对话：“平移、旋转和轴对称不改变图形的形状和大小。”“图形的放大和缩小只改变大小，不改变形状。”题中的问题和对话，隐含的意思是“平移、旋转和轴对称是不改变图形形状和大小的运动方式”。但如果教师叩问一下自己，就会意识到，在之前的教学中，从未明确地告诉过学生“轴对称是图形的运动”。所以，总复习时，若学生反问一句：“为什么轴对称也是图形的运动？”教师想必会很尴尬，也很难回答这一问题。

教师的教学很尴尬，教材的编写更尴尬。教材呈现上述的总复习内容之后，后续的几个习题只要涉及“图形的运动”，都只提对平移和旋转的要求，而不提对轴对称的要求。事实上，教材也的确没有安排“轴对称是图形的运动”的相关教学内容。人教版教材如此，其他版本教材也大同小异，感兴趣的读者可以翻阅各套教材的习题，细细体会。

综上所述，一个现实的挑战摆在教师面前：如何在六年级的总复习阶段，通过合适的教学，让即将小学毕业的学生能够认识到轴对称也是图形的运动，能够运用轴对称这种运动方式来解决相关问题？

因此，当笔者看到北师大版教材六年级下册第33页“试一试”时（如图1，此题是《义务教育数学课程标准（2022年版）》附录1课程内容中的实例），顿觉眼前一亮。这道题目的素材和要求只要稍作改动，就能巧妙地引导学生理解和接受轴对称就是一种运动，并且还能让学生以整体、联系的视角来审视轴对称、平移、旋转三种运动，在实现灵活运用数学知识的同时，又获得空间观念、创新意识的有益发展。

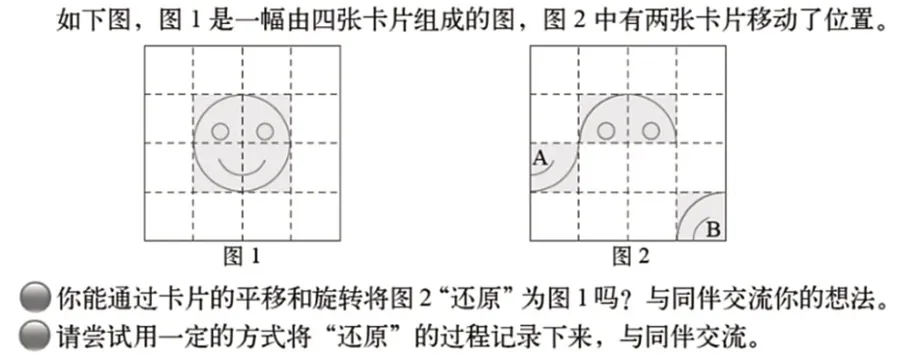
图1

【课堂实践】

一、借助情境，复习旧知

（一）回忆图形运动的方式

教师直接出示课题：“图形的运动”练习。

师：我们已经学过哪些图形的运动？

学生回答“有平移和旋转”，没有人说到“轴对称”。（教师板书：平移和旋转）

（二）唤醒图形运动的特点

师：今天我们就借助一个有趣的拼图游戏，把这些知识再理一理。（教师课件出示图2）这是一幅由四张卡片组成的笑脸拼图，一张①号卡片在拼图左边，一张②号卡片在拼图上面。如果要把这两张卡片各自还原到原来的位置，可以通过怎样的运动方式来实现呢？

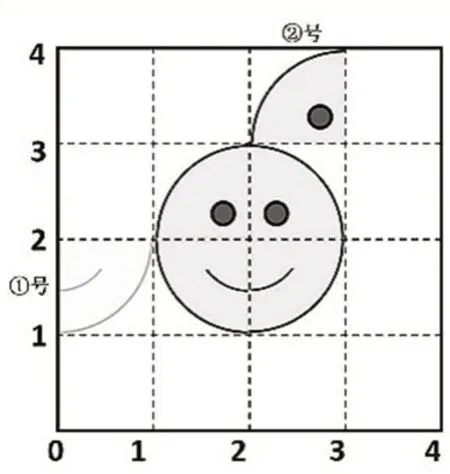
图2

1.复习平移。

生：①号往右平移两格就可以还原。

教师通过课件演示平移过程，引出平移运动的两个要素：方向、距离。（板书：方向、距离）

2.复习旋转。

师：①号图形成功还原。②号又该怎么还原？

学生能想到将②号卡片进行旋转，但在表述时讲不清楚绕哪个点或者遗漏旋转的方向。

师：要把这个点说清楚（手指着旋转中心），有一个很容易的办法。

课件出现表示行与列的数据，学生齐喊“数对”。教师再结合课件演示，引导学生完整地表达②号卡片的还原过程：绕点（2，3）顺时针旋转90°。强调旋转运动的三要素：旋转中心、方向和角度。（板书：旋转中心、方向和角度）

3.强调轴对称。

师：刚才我们运用平移和旋转顺利地还原了拼图。其实，①号图形还有其他的还原方式，你想到了吗？

生：可以把①号图形向右翻过去，连续翻两次。

教师请学生到屏幕前边比画边说明，课件同步演示卡片向右翻折的过程。

师：实际上这就是我们以前学过的轴对称，它也是图形运动的方式，运动前后的两个图形合在一起就是一个轴对称图形。我们再翻折一次，它就实现还原了（课件同步演示再翻折过程）。

教师说明这个过程是轴对称运动，告知学生把轴对称运动说成“翻折”更形象，同时强调轴对称运动要关注对称轴。

4.归纳共性。

师：这就是我们学过的三种图形运动的方式。请仔细观察，想一想，它们有什么共同的特点？

引导学生认识三种运动的共性是运动前后图形的形状、大小不变。（完善板书，如图4）

图3

二、动手操作，深度体验

（一）智慧风暴1——体验运动过程的多样性

教师课件出示图4。

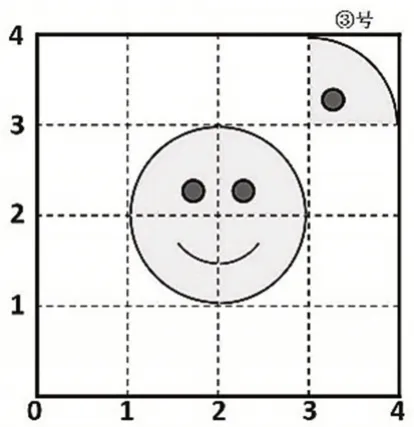
图4

师：我们来玩一个“智慧风暴1”的游戏。请看这幅笑脸拼图，一张③号卡片在拼图右上方，它可以通过哪些运动方式还原到原来的位置上？

学生先观察，再利用学具边摆边把运动过程表达清楚。学生都成功后，教师进行反馈。

生：先向左平移2 格，再绕点（2，3）逆时针旋转90°。

生：先以第3 列为对称轴翻折，再向左平移1格，最后向下平移1格。

生：先绕点（3，3）顺时针旋转90°，再绕点（3，2）逆时针旋转90°，最后以第2列为对称轴翻折。

……

为更好地训练学生的空间想象力，前两个学生反馈时，由学生到黑板前边摆边介绍，教师确认方法，统计学情；后面的学生反馈时，教师变换形式，先让学生口头描述③号图形的还原过程，再让其他学生根据听到的描述文字，想象整个运动的过程，并上台进行演示。

师：看来还原的方法有很多。老师也演示一种方法，你能不能看着电脑演示，然后用数学语言清楚地表达出来？

课件演示③号图形的另一种还原过程，引导学生规范准确地表达，教师顺势呈现运动过程的描述：先向左平移1格，再绕（2，3）逆时针旋转90°，最后向下平移1格。

（二）智慧风暴2——体验运动方法的灵活性

教师出示游戏规则：平移1格计一步，旋转1次计一步，轴对称（翻折）1次计一步。教师带领学生按上述规则统计刚才所用还原方式的步数，发现都是三步还原。

师：我们玩一个“智慧风暴2”的游戏，来挑战——两步能实现还原吗？

学生情绪激昂，教师让学生先观察、想象，再借助学具独立尝试，如果能两步还原的，用数学语言记录还原的过程。

师：两步还原成功了吗？谁来介绍一下你的方法？

生：先绕点（3，3）顺时针旋转180°（学生边口述过程边现场演示，如图5），再绕点（2，3）顺时针旋转90°。

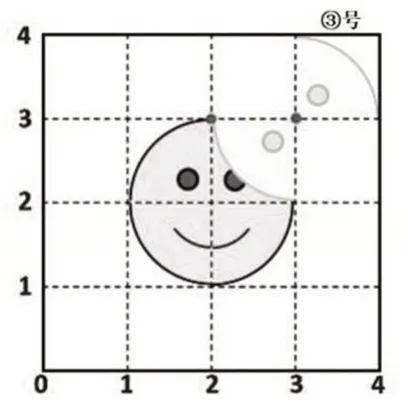
图5

生：先绕点（3，4）顺时针旋转90°（学生边口述过程边现场演示，如图6），再绕点（2，3）顺时针旋转180°。

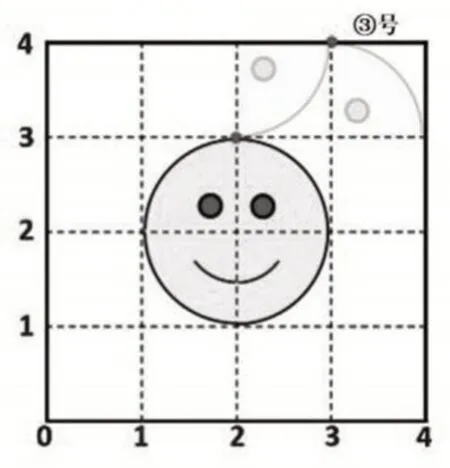
图6

师：两种方法都采用了两次旋转成功还原，你发现步数减少的窍门了吗？

学生感受到因为旋转角度的变化（变成180°），导致图形运动的幅度大，所以步数变少了。

生：先以点（4，1）和点（1，4）的连线为对称轴翻折，再绕点（2，2）顺时针旋转90°。（学生边口述过程边现场演示，如图7，学生听讲后都自发地鼓掌）

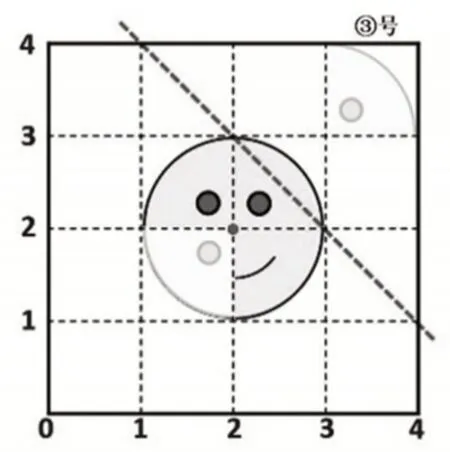
图7

生：我也是用轴对称的。先以2.5 列所在的直线为对称轴翻折一次，再向下平移一格。（学生边口述过程边现场演示，如图8，学生的掌声更热烈了）

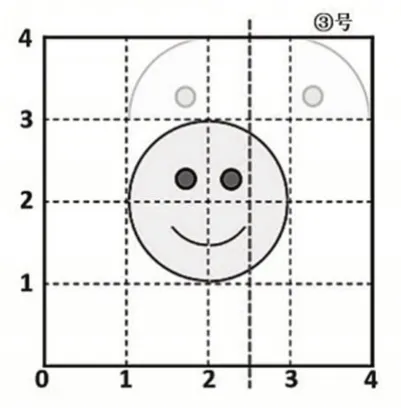
图8

……

学生体会到这些同学的窍门在于使用了多数同学没有想到的对称轴，使得图形运动的幅度变大，因此减少了步数。

师：对照自己两步还原的方法，看看是不是都用到了变大运动幅度这种策略。有不对的，自己再试一试，体验一下。

三、空间想象，提升思维

师：智慧风暴3——一步能否还原？请仔细观察、想象，发挥奇思妙想。如果有需要，也可以借助材料摆一摆、试一试。

学生踊跃探究，找寻特别的对称轴或者旋转中心（找对称轴的更多），但基本上都是失败的，大家普遍觉得一步是无法实现还原的。有个别学生说想到了方法，引起“轩然大波”。

师：有同学成功了，来展示你的方法吧！

生：把右上角这两个方格作为一个整体，绕点（3，2）逆时针旋转90°。

此时，有部分学生想象出了还原的过程，但还有不少学生不理解。教师适时借助课件，添加一条线，将线和③号拼图组合成一个“小红旗”（如图9），再引导学生想象运动过程，最后以动画演示，确认这个方法的确能一步还原。学生都忍不住热烈鼓掌表示佩服。

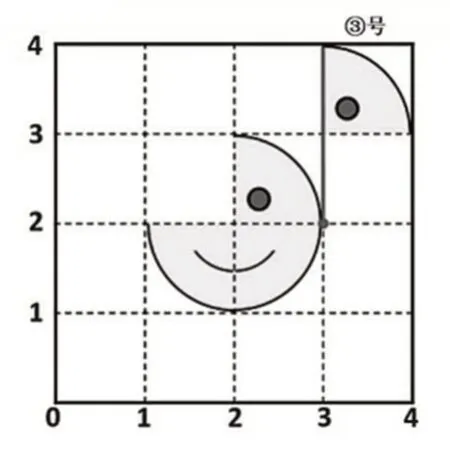
图9

师：一步还原的奥秘，靠的还是出乎常理的思维啊！除此之外，还有其他一步还原的方法吗？

四、课堂总结，升华经验

师：今天我们利用拼图游戏，复习了平移、旋转和轴对称三种图形的运动方式，大家对这三个知识的运用更灵活了。学了这节课的内容，你最大的收获是什么？

生：想问题时思维要发散，要敢于创新！

师：对的，只有创新思维，才能让我们取得突破。

【课后思考】

整个学习过程，以“笑脸还原”游戏为主线，学习氛围轻松愉悦，学生体验深刻到位，知识技能无痕落实，能力素养有效锤炼，较好地实现了预设目标。

一、轴对称巧妙融入运动，知识体系得以整体建构

引导学生理解和接受“轴对称”就是一种运动，是本教学设计最想直面的一个难点。教学设计顺应学情，先让学生运用平移和旋转还原图形，然后发挥学习材料的直观优势，启发学生思考“①号图形还可怎么还原”。此时，学生的生活经验发挥作用，“翻折”被顺势引出，再借助课件的支撑和语言的引导，“翻折就是轴对称，它也是图形的运动”就顺利地为学生所理解和接受了。

在此之后，学生面对“三步还原”“两步还原”“一步还原”等挑战性任务时，能主动运用三种运动方式，深入探寻解决问题的方法。此时，平移、旋转、轴对称，在学生心中的“地位”是完全一样的，甚至因轴对称的“特殊本领”，学生对这种运动还多了一些喜爱。最后，学生深刻地体会到了三种运动方式各自的特点和共同点，图形的运动（刚体运动）知识体系由此实现了整体建构。

二、教学的内涵充分挖掘，学生素养得以有效提升

众所周知，图形的运动知识教学中，发展学生的空间观念是重要的素养目标。整个教学过程中，观察、操作和想象三种发展空间观念的学习手段，通过精心设计获得了合理分布。观察在整个学习过程中贯穿始终，并被反复运用，使学生对三种运动的特征感知充分、印象深刻；操作被安排在最重要的环节——三步还原和两步还原，学生通过操作活动，对运动特点和过程有了直接体验，表象不断清晰；想象随着学生感知力的增强，有机地融入学习活动中，使学生逐步摆脱学具的束缚，从表象走向抽象。三个手段的灵活运用，让空间观念的培养落到了实处。另外，本内容的很多细节也是精心设计的，指向空间观念的培养，如学生展示方法时，有意要求学生仅用语言表述，其他学生边听边在头脑中想象还原过程，并演示过程。

此教学内容的另一个重要内涵就是创新意识的培养。三次“智慧风暴”，步数次次减少，逼着学生深入探索、提升思维。两步还原，学生在感受窍门之时，受到了大胆求变的思维影响；一步还原，虽困在其中，但当看到别人的成功经验时，创新的力量便深深地烙在他们心中。正因为如此，学生才会真切地总结道：“想问题时思维要发散，要敢于创新！”学生感受到创新的价值，愿意创新，追求创新，这是多么重要的收获啊！

对于图形的运动知识，如何以合适的方式引导学生释去心中疑惑，建构知识体系，提升素养能力，笔者作了粗浅的尝试。期待更多的教师能关注这个知识点，探索出更成熟、更有意义的教学之路。