形内自相似层级类蜂窝面外冲击特性研究

李 响，蔡明杰，徐兴兴，周绍国，焦元辰

(1.水电机械设备设计与维护湖北省重点实验室(三峡大学)，湖北宜昌 443002；2.三峡大学机械与动力学院，湖北宜昌 443002；3.三峡大学国际文化交流学院，湖北宜昌 443002)

随着工程领域对结构被动安全防护问题的日益重视，碰撞问题已经成为现代工程领域的一个重要的研究课题。对碰撞过程中结构的动力学行为进行研究和分析并设计出具有更高抗冲击性能的吸能缓冲结构，具有十分重要的工程意义。蜂窝结构具有质量轻，比强度、比刚度高，吸能缓冲性能优越等众多特点，被广泛应用于航空航天、汽车船舶、装甲防护等重要领域，因此对其冲击特性进行研究是十分重要的。近期研究表明[1-2]：在设计过程中引入含功能性基元，在微观尺度和宏观尺度上对材料结构进行改造设计，创造超材料性能的复合材料，将使材料的宏观物性大为提升。ARIGA等[3]使用纳米尺度的单元通过各种组合选择来生产功能材料，由简单单位组分富勒烯(C60和C70)零维单元进行组合转换成一维结构、二维形态、三维图案，甚至更复杂的层次结构，从而形成具有巨大形态变种的材料，拥有更广泛应用空间。杨德庆等[4]同样使用功能基元拓扑方法设计零泊松比(ZPR)功能超材料，通过有限元方法验证了该功能基元的零泊松比效应，并分析超材料试件的静、动力学特性，结果表明其具有更好的承载特性。霍鹏等[5]基于鹿角骨单位结构特征设计出了一种仿生薄壁管，并确定了该新型仿生薄壁管耐撞性的最优层数。单个胞元对性能的提升有限，将胞元按照相同或不同的形式在空间中进行堆垛排列，形成一种序构，该序构可有序或无序，亦或层级，其引发基元间的耦合，可对性能有更大的提升。而恰恰蜂窝胞元是功能基元的典型结构。RODERIC[6]对层级结构进行了定义，认为将层级结构引入到轻质多孔蜂窝结构中形成层级蜂窝结构，具有提高多孔材料强度与能量吸收性能的优点。AJDARI等[7]对具有自相似组织特性的层级蜂窝结构的面内力学性能进行了研究，发现一级和二级蜂窝比同质量的传统蜂窝在刚度方面均有较大提升。SUN等[8-9]对层级三角形薄壁管的冲击力学性能进行了研究，发现层级设计对薄壁管的抗冲击特性有较大提升。由“功能基元+仿生序构”，蜂窝胞元组成的蜂窝超材料结构展现出特殊的力学性能和应用前景，使得其逐渐成为未来轻量化、功能化材料/结构的理想选择。

“仿生学”的概念于1960年在美国第1次仿生学讨论会上被正式提出，通过研究生物结构、功能以及系统之间的相互作用来为工程技术领域提供相关的参考和指导。MILWICH等[10]由植物茎秆结构受到启发，提出了结构轻量化仿生设计原理。SPECK[11]根据植物茎秆的中空结构提出了变刚度设计的思想，以此实现结构的轻量化。ZOU等[12]根据竹子内部微观结构设计了仿竹薄壁管，研究表明，该新型仿生薄壁管相对于传统薄壁管具有优越的能量吸收性能。ZHU等[13]对羊角的力学性能进行理论分析以及对羊角微观结构进行观测，创新性设计了具有良好耐撞性能的仿生管。LI等[14]提出一种仿莲藕填充薄壁管结构(LFT)，经过分析和研究，该仿生薄壁管结构具有很高的能量吸收效率，能够提高车辆在正面碰撞载荷下的碰撞性能。HUANG等[15]以螳螂、虾、螯结构为原型，设计了一种仿生多胞薄壁管，采用LS-DYNA有限元分析软件建立多胞管多工况冲击下的有限元模型，并对其耐撞性进行优化。郭婷等[16]根据甲壳虫外壳设计出了仿甲壳虫芯柱并对模型进行优化，利用有限元方法研究优化后模型的耐撞性和抗冲击特性，同时与传统圆管进行对比分析，结果表明优化后的模型吸收能量更多，压缩载荷更加稳定，抗冲击性能更好，可将其应用在结构防撞性和能量吸收装置中。白中浩等[17]受甲虫鞘翅微观结构启发，提出了一种仿生微圆结构汽车吸能盒，发现该新型仿生微圆结构具有更加优越的耐撞性。霍鹏等[5]基于鹿角骨单位结构特征设计出了一种梯度仿生薄壁管，并确定了该新型仿生薄壁管耐撞性最优层数。生物材料结构是自然进化的结果，其在某些方面展现出独特的力学性能和优势，因此对生物结构材料进行分析研究和仿生设计对于材料结构功能一体化设计具有非常重要的参考价值和工程意义。

本文基于前期[18-21]研究基础，采用仿生原理和功能基元序构的设计思想，创新性提出一种新型形内自相似层级类蜂窝夹芯结构，并对其面外冲击特性进行分析，研究了层级因子、结构参数、胞元数目对该新型蜂窝结构冲击特性的影响，为设计出具有更强抗冲击力学性能的蜂窝材料提供理论依据和参考。

1 形内自相似层级类蜂窝结构的创新构型

1.1 仿生创新设计

如图1所示鹿角骨骼微观结构，在鹿角骨骼中存在大量并行排列的微圆结构，这些微圆结构被称为骨单位，骨单位主要由不同半径的同心圆骨板层层黏结而成。鹿角作为一种生物材料，具有高强度、刚度、韧性以及抗冲击的能力，而这些性质又密切相关于其独特的微观结构[22]，因此，鹿角骨骼中微圆结构与鹿角整体优良的力学性能以及抗冲击能力密切相关。传统六边形蜂窝的动、静态力学性能已有大量研究，因此，在传统六边形蜂窝的基础上，利用鹿角骨骼中的特殊微圆结构，创新性设计出一种形内自相似层级类蜂窝结构。根据对鹿角骨骼基本特征的提取以及相应的演化设计，本文所设计的形内自相似层级类蜂窝胞元结构如图2所示，其主要包括零级胞元(见图2 a))、一级胞元(见图2 b))、二级胞元(见图2 c))。其中零级胞元为正六边形，一级胞元则是在零级胞元的6个顶点向中心延伸并加入微圆结构形成的层级胞元结构，二级胞元是在一级胞元微圆结构内进行更进一步地层级设计形成的一种更高层级的胞元结构，以此类推。形内自相似层级类蜂窝夹芯由上述不同层级的胞元结构通过周期性排列而成，蜂窝级数与零级胞元内圆形结构个数一一对应。

图1 鹿角骨骼微观结构

图2 形内自相似层级类蜂窝单胞结构

1.2 几何尺寸

自相似层级类蜂窝胞元结构及结构尺寸如图3所示，其主要包括零级胞元、一级胞元、二级胞元。首先，3种层级的胞元结构最外沿均为正六边形，且其胞壁长度均为l；零级蜂窝胞元壁厚记为t0，一级蜂窝和二级蜂窝分别记为t1和t2；一级胞元内部的微圆结构半径记为r1，二级胞元中的二级微圆结构的半径记为r2,同时文中所有蜂窝夹芯沿面外方向的厚度均记为h，且尺寸关系满足l=2r1=4r2。

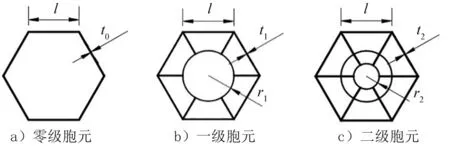
图3 形内自相似层级类蜂窝单胞结构尺寸

2 数值计算结果及讨论

2.1 有限元模型建立及实验验证

利用ABAQUS/Explicit显式动力学模块建立的形内自相似层级类蜂窝结构面外冲击有限元数值计算模型如图4所示，该模型具体由上、下刚性面板以及中间蜂窝夹芯3部分组成。计算过程中对下刚性板进行固定约束，对上刚性板分别施加10，20和30 m/s的恒定冲击速度。模型中对蜂窝夹芯采用四节点缩减积分壳单元S4R单元进行网格划分，厚度方向设置5个积分点，刚性板则采用实体单元进行网格划分，为了同时保证计算精度和效率，将蜂窝网格大小设置为0.3 mm，刚性板网格大小设置为0.5 mm。蜂窝与刚性板之间的接触设定为通用接触，其中静摩擦系数和动摩擦系数分别置为0.3和0.2。蜂窝基体材料选用铝合金AA3003-H18，其力学性能具体如下：密度ρs=2 700 kg/m3，弹性模量Es=69 GPa，屈服应力σs=115.8 MPa，泊松比为0.33。3种蜂窝胞壁长度l均取5 mm,蜂窝面外厚度h均取24 mm。蜂窝结构壁厚尺寸在2.4节讨论。为了验证面外冲击有限元数值计算模型的准确性，对零级蜂窝进行面外冲击数值模拟。

图4 面外冲击有限元数值计算模型

图5为数值计算与实验结果对比[23]，由图5可知，数值计算结果和实验结果吻合较好，证明了有限元数值计算模型的可靠性。

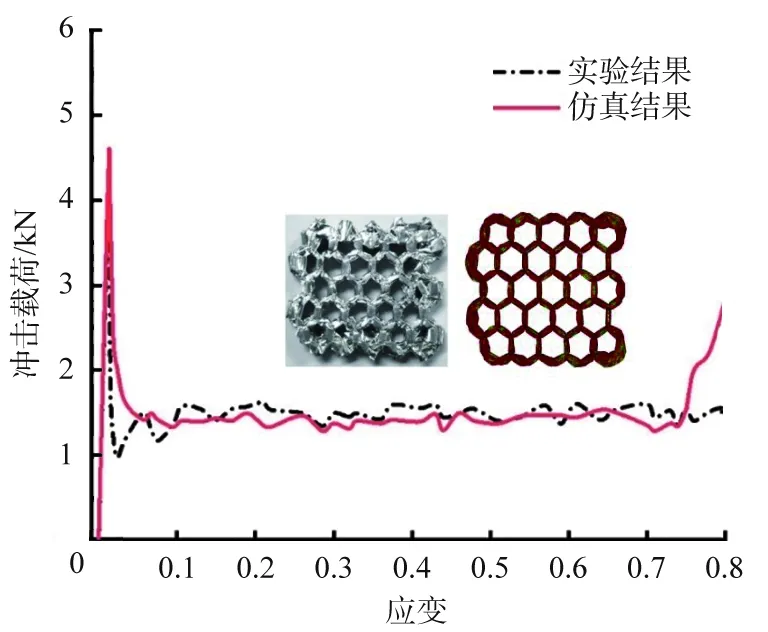
图5 零级蜂窝面外冲击有限元数值模拟结果与实验对比[23]

2.2 耐撞性评价指标

夹层结构的主要耐撞性指标包括总吸收能量(EA)、比吸能(SEA)、峰值碰撞力(PCF)、平均碰撞力(MCF)以及载荷效率(CFE)等。SEA是指结构单位质量的吸能率，是最关键的吸能效率指标，其可表示为

(1)

式中：M为结构质量；EA表示结构在塑性变形过程中的总吸收能量，其方程为

(2)

式中：d为有效压缩位移；F(x)为冲击过程瞬态冲击力。PCF和MCF与乘员的安全密切相关。CFE为平均载荷与碰撞峰值载荷的比值，具体可表示为

(3)

(4)

其中CFE越高，表示载荷稳定性就越高。

2.3 数值模拟

如图6所示，蜂窝夹芯结构在受到冲击载荷时典型的压溃力-应变曲线，包含了具有明显不同特征的4个阶段：阶段Ⅰ为线弹性阶段，蜂窝芯层发生弹性变形；阶段Ⅱ为塑性屈曲变形阶段，此阶段蜂窝芯层坍塌，发生失效；阶段Ⅲ为应力平台区，是蜂窝芯材的主要能量吸收区，经大量实验和仿真研究证明，应力平台区越长，结构的能量吸收效果越好；阶段Ⅳ为密实化阶段，蜂窝芯层压缩变形逐渐积累，直至密实化，此时结构的变形增量减小，结构整体能量吸收效率降低。

图6 冲击载荷作用下典型的压溃力-应变曲线

2.3.1 等相对密度

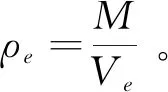
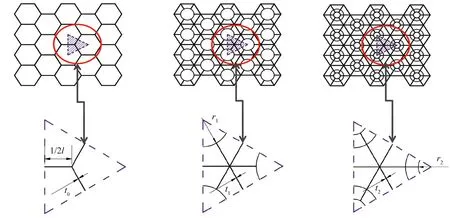
图7 形内自相似层级类蜂窝夹芯拓扑结构代表单元体示意图

为保证蜂窝整体截面积相等，即等相对密度。经计算，此时，零级、一级和二级蜂窝结构壁厚如表1所示。由表1中的不同层级蜂窝结构壁厚数值得到的各级蜂窝结构模型如图8所示。

表1 不同层级蜂窝壁厚

图8 等相对密度形内自相似层级类蜂窝模型

2.3.2 变形模式

图9反映了不同层级蜂窝在等相对密度条件下，其面外冲击速度作用下的变形模式。由图9 a)可以看出，在10 m/s冲击速度作用下，3种层级的蜂窝均是从远离冲击板的一端开始发生压溃变形；由图9 b)和图9 c)可知，当冲击速度为20 m/s和30 m/s时，起始变形区域开始向冲击端转移，这是惯性效应增强导致的结果。三者之间最为明显的差异是折叠波长会随蜂窝层级的改变而发生变化，从数值模拟结果来看，折叠波长会随蜂窝层级的提升而变短，波长越短，压缩就会更加充分，结构能量吸收效率就会越高。同时，也可以发现，在不同速度冲击载荷作用下，不同层级蜂窝结构的压缩变形过程均很稳定，满足工程领域对吸能构件的基本需求。

图9 层级蜂窝在不同冲击速度作用下的变形模式

2.3.3 动力学响应与能量吸收特性

图10为不同层级蜂窝在等相对密度条件下受到面外冲击载荷时的压缩反力-位移曲线。由图10可以看出，在不同冲击速度作用下，平台压缩反力随着蜂窝层级的提升而提升，但并不明显。虽然峰值碰撞力有所增大，但是由图11、图12可以看出，其载荷效率及比吸能仍然随着层级的增加而增加。尤其在10 m/s冲击速度作用下，CFE及SEA的提升受层级因子影响最为明显。在10 m/s冲击速度作用下，一级蜂窝和二级蜂窝的载荷效率相比于零级蜂窝分别提升21%和40%，比吸能分别提升11%和28%。层级设计可以有效提升蜂窝结构的比吸能和载荷效率。

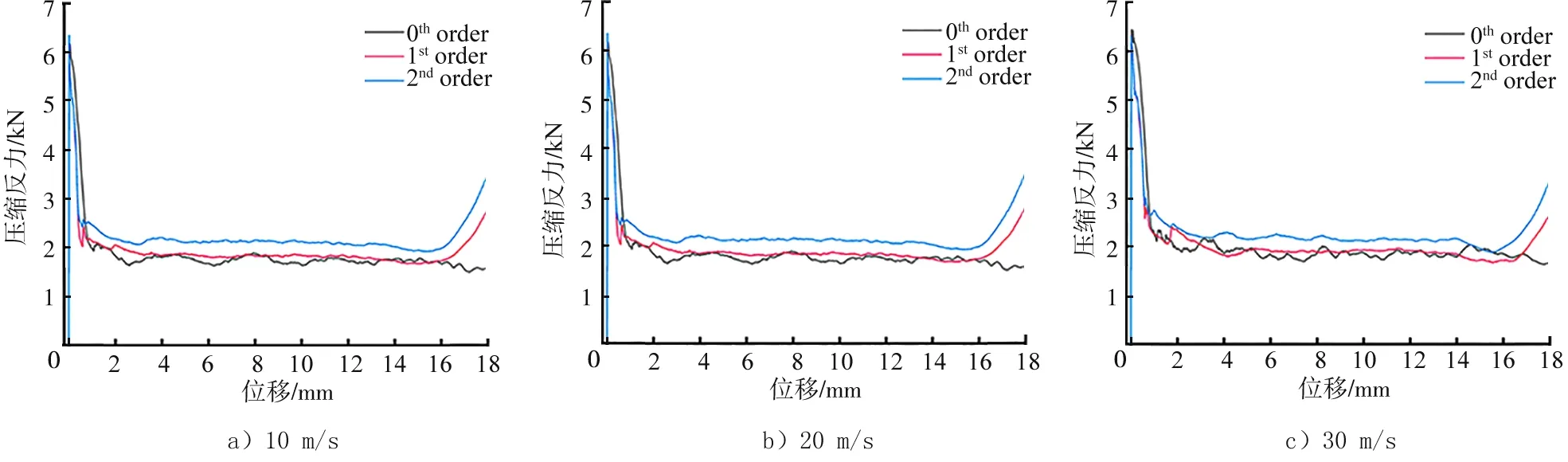
图10 不同层级蜂窝的压缩反力-位移曲线

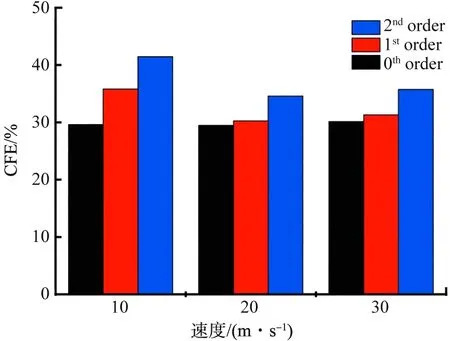
图11 不同层级蜂窝的载荷效率对比

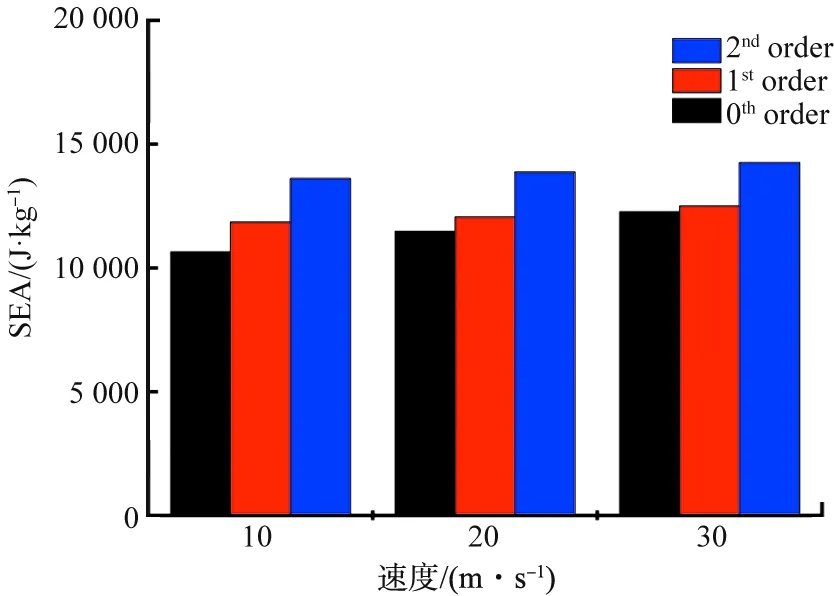
图12 不同层级蜂窝的比吸能对比

2.4 等壁厚

当一级、二级蜂窝与零级蜂窝壁厚相等时，3种蜂窝结构壁厚为t0=t1=t2=0.1 mm。图13表示不同层级蜂窝在壁厚均为0.1 mm时的有限元模型。

图13 等壁厚形内自相似层级类蜂窝模型

2.4.1 变形模式

图14反映了不同层级蜂窝在等壁厚条件下，其面外冲击速度作用下的变形模式。层级蜂窝分别在10，20和30 m/s速度冲击载荷作用下的变形模式，与等相对密度条件下的变形模式基本相同。由图14 a)可以看出，在10 m/s冲击速度作用下，3种层级的蜂窝均是从远离冲击板的一端开始发生压溃变形；由图14 b)和图14 c)可知，当冲击速度为20 m/s和30 m/s时，起始变形区域开始向冲击端转移。由于本研究中壁厚尺寸选取的局限性，在2种壁厚条件下，其变形模式基本相同。

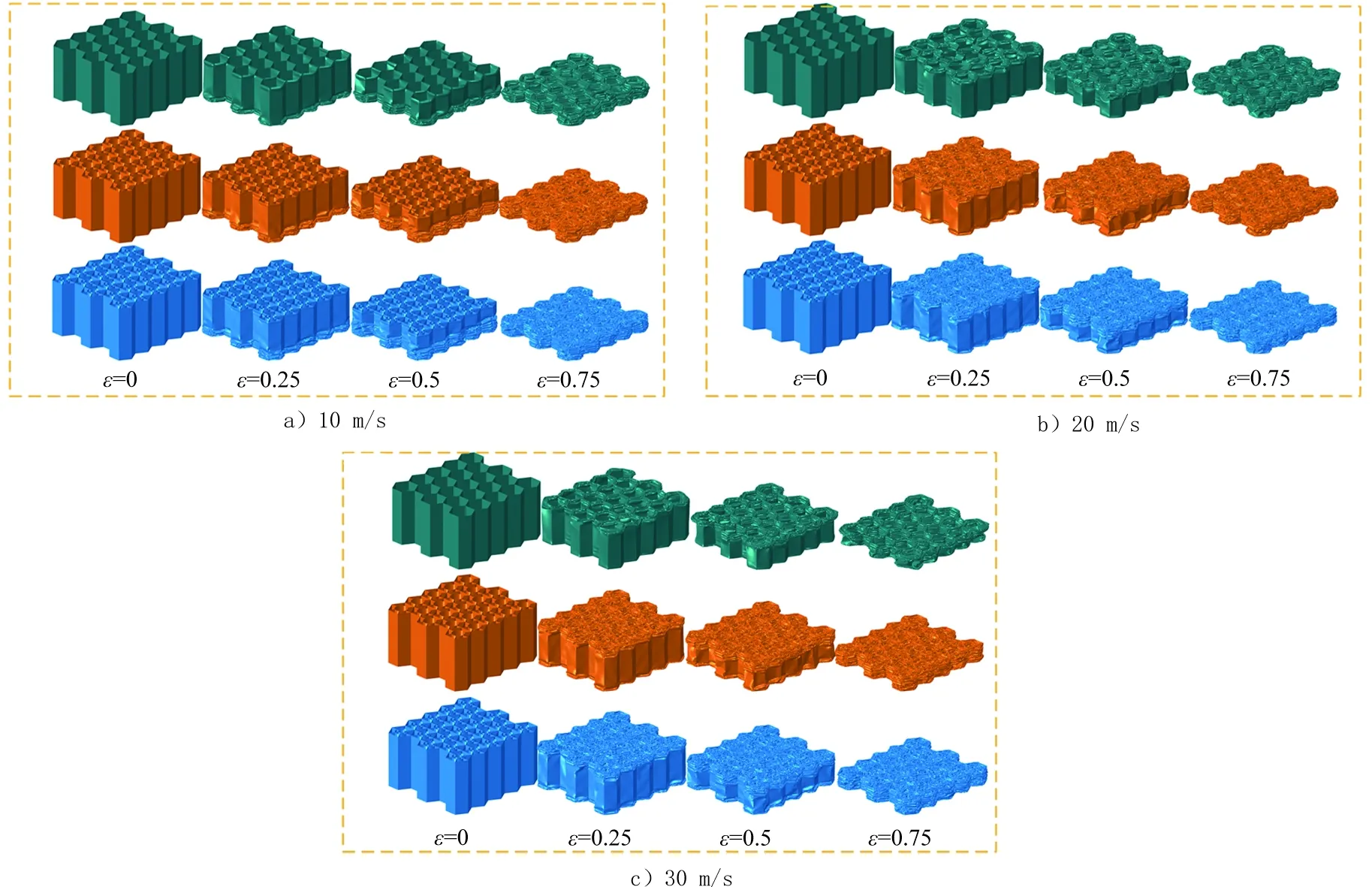
图14 层级蜂窝在不同冲击速度作用下的变形模式

2.4.2 动力学响应与能量吸收特性

图15为不同层级蜂窝在等壁厚面外冲击速度作用下的压缩反力-位移曲线。由图15可以看出，在不同冲击速度作用下，平台压缩反力会随着蜂窝层级的提升而急速提升，虽然峰值碰撞力有所增大，但是由图16、图17可以看出，其CFE及SEA还是随着层级的增加而增加并且效果是十分显著的。在10 m/s冲击速度作用下，一级蜂窝和二级蜂窝的载荷效率相比于零级蜂窝分别提升77%和115%，比吸能分别提升72%和116%。

图15 不同层级蜂窝的压缩反力-位移曲线

图16 不同层级蜂窝的载荷效率对比

图17 不同层级蜂窝的比吸能对比

通过对等相对密度以及等壁厚2种情况下的形内自相似类蜂窝夹芯结构进行冲击载荷状态下的数值模拟，可以得到以下结论：蜂窝结构受层级影响，其能量吸收效率以及比吸能会随着层级的提高而提高，层级设计可以有效提升蜂窝结构的能量吸收性能。

3 有限元模型的理论验证

采用简化的超折叠单元理论建立形内自相似层级类蜂窝结构面外压缩理论模型[24]。该理论认为当薄壁结构受到面外冲击载荷作用时，系统能量保持守恒。外力做功被薄壁结构以弯曲能和延展能的形式散耗，对于一个完整的折叠单元，存在以下表达式：

Pm×2H×k=Ub+Um，

(5)

式中：Pm为压缩过程中的平均压缩力；2H表示折叠波长度；k为单个折叠单元实际压缩长度与总长度的比值，其范围在0.7～0.8之间[25]；Ub和Um分别为一个折叠单元在压缩过程中耗散的弯曲吸能和延展吸能。图18 a)为折叠单元发生压缩时折叠波形成示意图，由图18 a)可知一个折叠波形成时，会产生3条塑性铰链，折叠单元的弯曲能可通过三塑性铰链的弯曲能求和得到，即

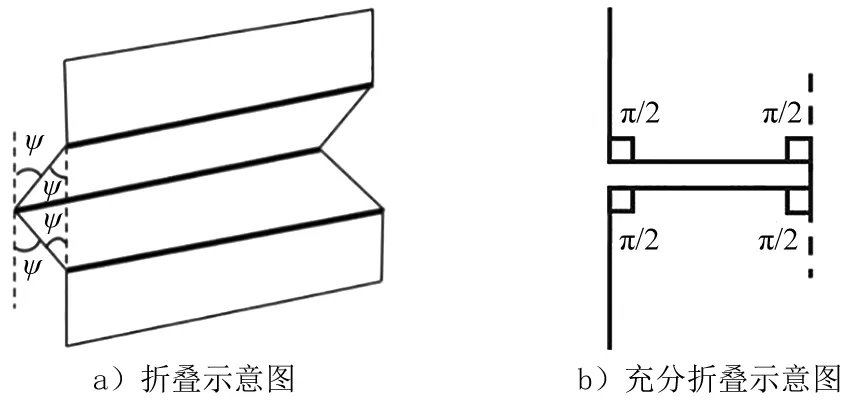
图18 基本折叠单元变形模式

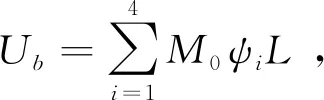
(6)

(7)

Ub=2πM0L。

(8)

对于具有多个折叠单元的薄壁结构，总延展能为所有折叠单元延展能的总和，具体可表示为

Um=NMm，

(9)

式中：N为折叠单元的数目；Mm为单个折叠单元的延展能。

在零级蜂窝中存在2种折叠单元，分别是1型单元和2型单元，其具体结构如图19所示。

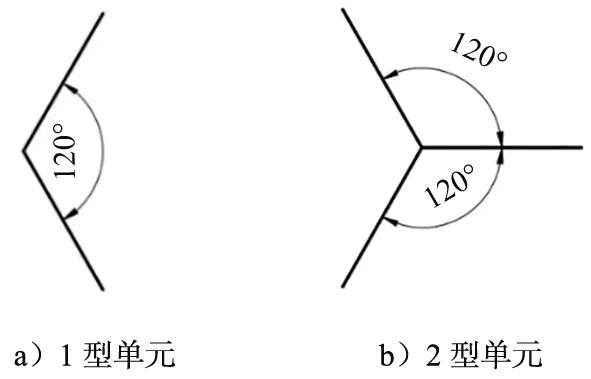
图19 零级蜂窝中的折叠单元示意图

对于1型单元，其延展能可表示为[24]

(10)

对于2型单元，其延展能则可表示为[20]

(11)

对于具有n×n胞元排列的零级蜂窝结构，其总延展能可表示为

Um0=N1M1+N2M2，

(12)

式中

(13)

因此，零级蜂窝的总延展能可表示为

(14)

零级蜂窝截面总长度L0可表示为

L0=(3n2+2.5n+0.5)l，

(15)

则零级蜂窝总弯曲能可表示为

Ub0=2πM0L0。

(16)

将式(14)、式(16)代入式(5)，得

(17)

根据准静态条件，有

(18)

根据式(18)可推导出H的表达式：

(19)

将式(19)代入式(17)，可求得

(20)

若蜂窝轴向长度为d，当其充分压缩时，结构总能量吸收可表示为

(21)

结构比吸能可表示为

(22)

一级蜂窝中存在4种折叠单元，4种折叠单元分别如图20所示。

图20 一级蜂窝中的折叠单元示意图

对于3型单元，其延展能可表示为

(23)

对于4型单元其延展能则可表示为

(24)

对于5型单元其延展能则可表示为

(25)

对于6型单元其延展能则可表示为[17]

(26)

对于具有n×n胞元排列的一级蜂窝，其总延展能可表示为

(27)

式(27)中

(28)

此时，一级蜂窝的总延展能可表示为

(29)

一级蜂窝截面总长度可表示为

L1=(3n2+2.5n+0.5)l+(n2-0.5n+0.5)(π+3)l，

(30)

则一级蜂窝总弯曲能可表示为

Ub1=2πM0L1，

(31)

(32)

若蜂窝轴向长度为d，当其充分压缩时，结构总能量吸收可表示为

(33)

结构比吸能可表示为

(34)

在二级蜂窝中，存在5种折叠单元，其具体结构如图21所示。

图21 二级蜂窝中的折叠单元示意图

对于7型折叠单元，其延展能可表示为

(35)

对于具有n×n胞元排列的二级蜂窝，其总延展能可表示为

(36)

式中

N7=6n2-3n+3。

(37)

此时，二级蜂窝的总延展能可表示为

(38)

二级蜂窝截面总长度可表示为

(39)

则二级蜂窝总弯曲能可表示为

Ub2=2πM0L2。

(40)

可求得

(41)

若蜂窝轴向长度为d，当其充分压缩时，结构总能量吸收可表示为

(42)

结构比吸能可表示为

(43)

对于N级蜂窝，截面总长度为

(44)

因此，总弯曲能可表示为

UbN=2πM0LN。

(45)

总延展能可表示为

(46)

可求得

(47)

若蜂窝轴向长度为d，当其充分压缩时，结构总能量吸收可表示为

(48)

结构比吸能可表示为

(49)

为了验证上述理论模型的正确性，将零级蜂窝相关参数代入式(20)中可求得Pm=1.77 kN。将理论计算和数值模拟结果进行对比可得到如图22所示的曲线图。从图中可以看出，理论计算与数值模拟整体吻合良好，只是在冲击过程后半段误差略有增大，这是因为在冲击过程后半段，蜂窝失稳导致平台压缩反力下降造成的。不过从整体来看，以上误差均在可接受范围内，证明上述理论模型具有较高的可靠性，可为后续研究提供理论基础。

图22 零级蜂窝面外冲击数值模拟结果与理论计算对比

4 结构尺寸和胞元数目对形内自相似层级类蜂窝面外冲击特性的影响

基于上述理论模型，研究了胞元壁厚t、胞壁长度l以及胞元数目n对形内自相似层级类蜂窝结构面外冲击平均压缩反力和比吸能的影响，结果如图23、图24所示。由图23可知，在面外冲击载荷作用下，不同层级蜂窝结构平均压缩反力会随胞壁长度和胞元壁厚的增大而增大，并且胞元壁厚的影响会更加显著。由图24可以看出，不同层级蜂窝的比吸能会随蜂窝壁厚的增大而增大，随胞壁长度的增大而不断减小。这2种情况并不矛盾，胞壁长度以及胞元壁厚的增大均会导致冲击过程中压缩反力的提升，但是二者的影响效果并不相同。

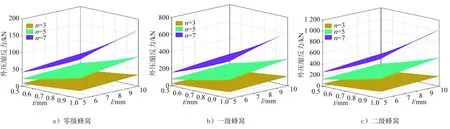
图23 结构尺寸和胞元数目对不同层级蜂窝面外压缩反力的影响

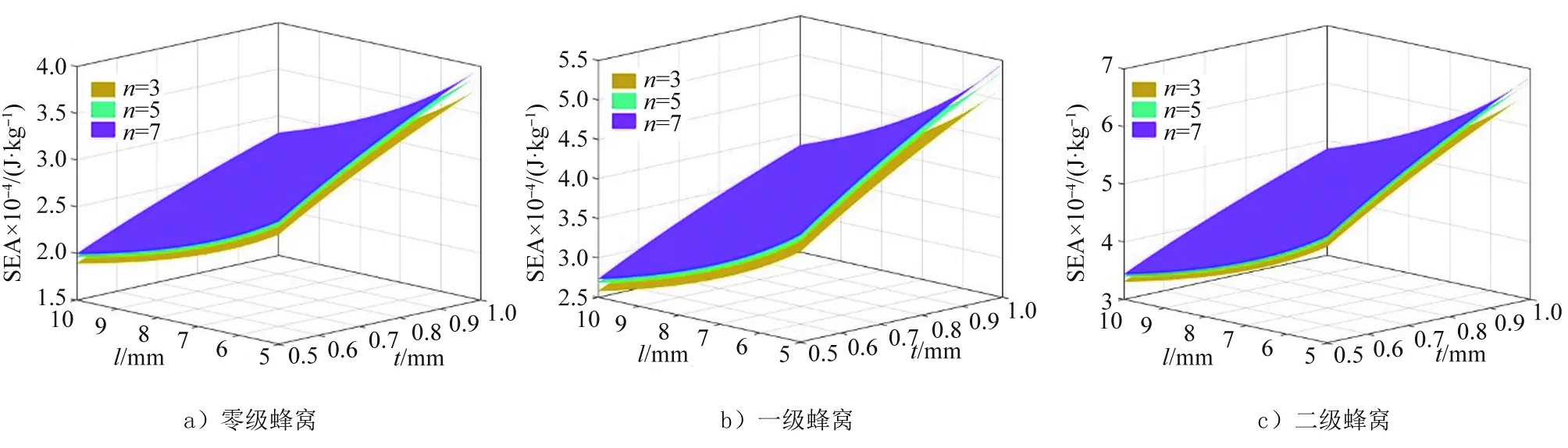
图24 结构尺寸和胞元数目对不同层级面外冲击比吸能的影响

图25反映了在特定结构尺寸下，胞元数目对不同层级蜂窝比吸能的影响。由图25可以看出，胞元数目对蜂窝结构的比吸能是有较大影响的，并且随着胞元数目的增大，不同层级蜂窝比吸能开始收敛为一个稳定值。在相同结构参数下，胞元数目为20的零级蜂窝、一级蜂窝、二级蜂窝的比吸能相比于单胞的零级蜂窝、一级蜂窝、二级蜂窝分别提升30.0%，28.1%和17.0%。同时，从图24中也可以看出蜂窝层级对结构比吸能的影响，当胞元数目为20时，一级蜂窝的比吸能较零级蜂窝提升36.9%，二级蜂窝的比吸能较一级蜂窝提升24.7%。综上所述，结构尺寸以及胞元数目均会对形内自相似层级类蜂窝面外冲击性能产生较大影响，其中增大胞元壁厚、减小胞壁长度以及增加胞元数目均能使结构的比吸能得到较为明显的提升。

图25 特定尺寸下胞元数目对层级蜂窝比吸能的影响

5 结 论

由生物材料鹿角受到启发，在传统六边形的基础上，融合鹿角骨骼中的微圆结构，创新性设计了一种形内自相似层级类蜂窝结构。首先，建立了传统六边形蜂窝，以及一、二级层级蜂窝在面外方向上恒定速度冲击的有限元模型。利用数值模拟和理论相结合的方法对其面外冲击特性进行了分析和研究，并得到了如下结论。

1)在面外冲击载荷作用下，对等相对密度及等壁厚2种结构条件下的蜂窝结构分别进行数值模拟，形内自相似层级类蜂窝结构相较于传统蜂窝结构有更高的能量吸收率以及载荷效率。

2)基于简化的超折叠理论建立了形内自相似层级类蜂窝结构面外冲击理论模型，验证了该理论模型的可靠性，可为该新型蜂窝在工程应用中的耐撞性优化设计提供理论参考。

3)通过数值模型，进一步探究了蜂窝结构尺寸和胞元数目对其面外冲击性能的影响。结构参数和胞元数目对形内自相似层级类蜂窝面外冲击性能影响较大，其中增大蜂窝壁厚、减小胞壁长度以及增加胞元数目均能使结构的比吸能得到有效提升。

4)结构的比吸能会随着胞元数目的增加而增大，但是当胞元数目增加到一定规模时，结构的比吸能会趋于一个稳定值。

层级结构设计可有效提高蜂窝结构的抗冲击性能，对于形内自相似层级类蜂窝结构而言，在不同方向上具有不同的力学性能，未来还需对该类蜂窝结构的面内力学性能进行研究，以及对形内自相似层级类蜂窝结构尺寸进行优化设计 ，使之在特定的尺寸条件下具有更优越的力学性能参数，使整体结构质量更轻，为结构轻量化设计提供一种新思路。