基于ψ-(h,r)-凹算子的非线性分数阶(p,q)-差分方程的唯一迭代解
王菊芳,王 斯,禹长龙,2
(1.河北科技大学理学院,河北石家庄 050018;2.北京工业大学理学部,北京 100124)
量子微积分又称q-微积分。1909年,JACKSON[1]首次提出量子微分与积分的定义。量子微积分作为数学发展中的一个新兴学科,广泛应用于数学、物理等自然科学领域。众所周知,许多实际问题都可归结为q-差分方程可解性的研究。近年来,人们对q-差分方程的可解性理论已获得许多重要的结果[2-4]。20世纪中期,AL-SALAM[5]与AGARWAL[6]对q-微积分进行拓展,给出了分数阶q-微积分的相关理论。与q-微积分相比,分数阶q-微积分的应用更为广泛,激发了广大学者对分数阶q-微积分的研究热潮,分数阶q-差分方程的可解性理论得到了迅速发展[7-12]。
作为q-微积分的进一步拓展,双参数量子微积分应运而生,即(p,q)-微积分,最早出现在1990年的文献中[13]。(p,q)-微积分在差分方程、组合数学、数论、力学、物理科学等领域得到了重要应用[14-20]。2020年,SOONTHARANON等[21]引入分数阶(p,q)-微积分的概念,研究了分数阶(p,q)-微积分的性质且得到与经典微积分类似的相关定理与结论。但关于非线性分数阶(p,q)-差分方程可解性的研究结果并不多[22-23]。例如:2019年,GHOLAMI[19]研究了非线性的二阶(p,q)-差分方程
的可解性,利用正锥上的Krasnosel′skii不动点定理证明了该问题正解的存在性、多重性和不存在性,还研究了相应的双参数量子特征值问题,根据Lyapunov不等式给出了正特征值的下界估计;2020年,SOONTHARANON等[22]利用Banach不动点定理及Schauder不动点定理,研究了一类具有非局部Robin边界条件的分数阶(p,q)-差分方程
为了丰富分数阶(p,q)-差分方程边值问题的基本理论,基于上述工作,笔者运用定义在有序集上增的ψ-(h,r)-凹算子的不动点定理,研究非线性分数阶(p,q)-差分方程边值问题
(1)
的可解性,其中0 定义1[18]设α是任意常数,则 其中 定义3[21](p,q)-Gamma和(p,q)-Beta函数定义为 定义4[18]函数f(x)的(p,q)-导数为 若f在x=0处可微,则Dp,qf(0)=f′(0)。 其中,tDp,q关于t是(p,q)-可微的。 引理3[21]设α,β>0,0 引理4[21]设α∈(N-1,N),N∈,0 有关凹算子的相关理论如下。 定义7[11]对于任意x,y∈X,称x与y等价,若存在μ>0和ν>0,使得μx≤y≤νx,记为x~y。 对于给定的h>θ,定义集合Ph={x∈X|x~h},显然Ph⊂P。设r∈P且θ≤r≤h,定义Ph,r={x∈X|x+r∈Ph},即Ph,r={x∈X|存在μ=μ(h,r,x)>0,ν=ν(h,r,x)>0,使得μh≤x+r≤νh}。 显然,Ph=Ph,θ。 定义8[24]设T:Ph,r→E是给定算子,满足任意x∈Ph,r,λ∈(0,1),存在ψ(λ)>λ,使得T(λx+(λ-1)r)≥ψ(λ)Tx+(ψ(λ)-1)r,则称T是ψ-(h,r)-凹算子。 本文用到的假设如下: (H3)f(t,0)≥0且对于t∈[0,1],有f(t,0)≢0; (H4)1-δηα-2≤p(1-δηα-1); (H5)pα-qα≥pα-1-qα-1。 P={ω∈X|ω(t)≥0,t∈[0,1]}。 若ζ>0,为方便起见,记 (2) 且 其中 (3) 引理7设y∈C[0,1],0<δηα-2<1且η∈(0,1),则分数阶(p,q)-差分方程边值问题 (4) 有唯一解, 其中: 证明设ω(t)是式(4)的一个解,由引理4得,边值问题(4)可以等价为积分方程: 其中,c1,c2,c3是未知常数。由边界条件ω(0)=(Dp,qω)(0)=0可得,c2=c3=0。此时, 又由(Dp,qω)(1)=δ(Dp,qω)(η),有 因此, 证毕。 是连续的; 证明如下。 性质1):显然成立。 性质3):显然成立,证毕。 证明若t∈[0,1],则有 且 则0≤r(t)≤h(t),即r∈P。此外,Ph,r={ω∈X|ω+r∈Ph}。 根据引理3和引理7可知,若边值问题(1)有解ω(t),则 因此,对于任意ω∈Ph,r和t∈[0,1],定义算子 显然,ω(t)是边值问题(1)的解,当且仅当ω(t)是算子T的不动点。 首先证明T:Ph,r→X是ψ-(h,r)-凹算子。对于任意λ∈(0,1),ω∈Ph,r,由假设(H2)得 ψ(λ)r(t)+[ψ(λ)-1]r(t)=ψ(λ)Tω(t)+[ψ(λ)-1]r(t), 即T(λω+(λ-1)r)≥ψ(λ)Tω+[ψ(λ)-1]r,λ∈(0,1),ω∈Ph,r,由定义8知T是ψ-(h,r)-凹算子。 其次证明T:Ph,r→X是增的。由于ω∈Ph,r,则ω+r∈Ph,故存在ι>0使得ω(t)+r(t)≥ιh(t),则有 由假设条件(H1)可知T:Ph,r→X是增的。 最后,证明Th∈Ph,r,只需证明Th+r∈Ph。由引理8和假设条件(H1),有 且 Γp,q(α)>0且H*>0,由假设(H1)和(H3)可知: 故μ≥ν>0,即Th+r∈Ph。 注4若定理1的条件成立,且有下列不等式: 则边值问题(1)在Ph,r中有唯一非平凡解。同理,可构造迭代函数列来逼近该非平凡解。 下面讨论当δ=0时边值问题(1)的可解性。 推论1若条件(H1)-(H3)和(H5)成立,则分数阶(p,q)-差分方程边值问题 (5) 有唯一解ω*∈Ph,r。此时,对于任意φ0∈Ph,r,定义迭代序列 则当n→∞时,φn(t)→ω*(t)。 证明类似于定理1的证明。 注5若ζ=0,根据引理6,类似地可以证明边值问题(1)正解的唯一性。 考虑非线性分数阶(p,q)-差分方程边值问题 (6) 经简单计算,可知 h(t)=H*t3/2, 且 于是有 且 及 且f(t,0)≢0。于是,假设条件(H1)和(H3)成立。 2)函数f可表示为 且 又 本文应用定义在有序集上增的ψ-(h,r)-凹算子不动点定理,研究了一类非线性分数阶(p,q)-差分方程边值问题解的存在唯一性,通过构造迭代序列逼近唯一非平凡解。在赋予非线性项f一定的条件下,非线性分数阶(p,q)-差分方程具有唯一非平凡解。研究结果在一定程度上丰富了分数阶(p,q)-差分方程的可解性理论,为分数阶(p,q)-差分方程在空气动力学、复杂介质电动力学及电路等领域的应用提供了理论基础。今后,将利用上下解、变分迭代等方法,深入研究分数阶(p,q)-差分方程的可解性。1 预备知识
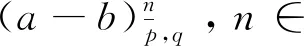
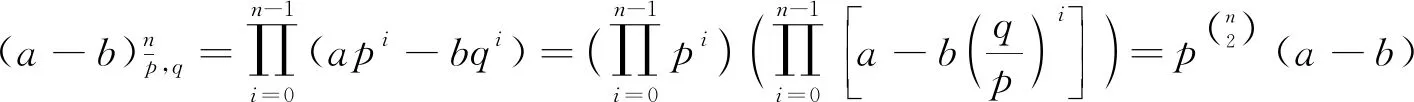


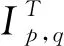

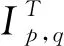
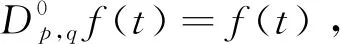

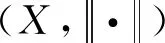
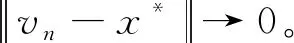
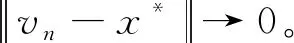


2 主要结论







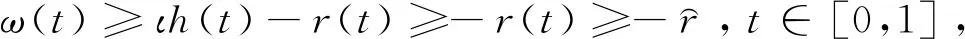
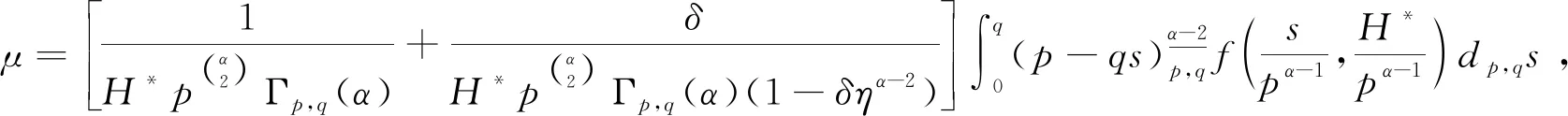
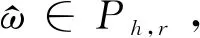
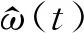

3 应用举例

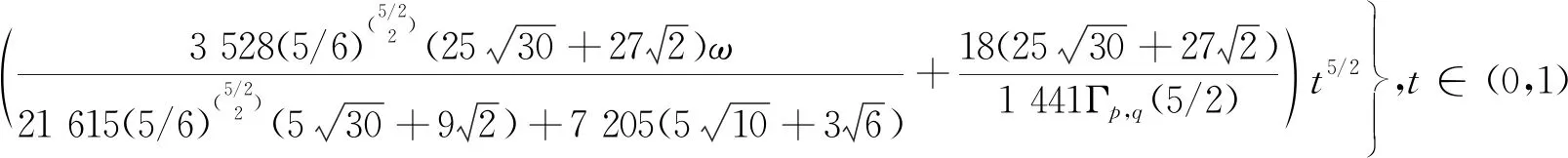

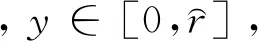



4 结 语

