融合多因素的“时间齿轮”交通流预测模型

兰添贺，曲大义，陈 昆，刘浩敏

(青岛理工大学机械与汽车工程学院，山东青岛 266520)

随着智能交通及大数据技术的快速发展，运用智能化手段解决城市交通问题成为一种主流趋势[1]。车载传感器和路口监控能够实时收集大量的交通流量数据，通过提取并挖掘数据中的隐藏规律，可以为减缓交通压力、优化出行结构和提升道路通行能力等提供帮助。因此，对交通流影响因素的深度分析，以及对交通流进行实时准确的预测，是目前城市交通领域研究的热点。

为了提升交通流预测的准确度，国内外研究人员提出了多种预测方法[2-10]，相比于传统的数学模型预测方法[11]，这些方法虽在预测精度和效率上取得了很大进步，但仅考虑了单一因素，也缺少对影响交通流的各因素进行深度特征挖掘。随着人工神经网络的快速发展，依托深度学习算法进行交通流的特征挖掘和预测，成为全新的研究方向[12-16]。一些模型虽通过人工神经网络深度挖掘了交通流信息的时间特征，但却忽略了外部天气因素和空间因素的重要性。融合多源数据并结合多种算法虽能够明显提升交通流预测的准确度，但并没有考虑城市道路交通自身拥有的特点[17-21]。城市道路的布局结构与高速公路不同，市区城市道路具有密集路网和大量交叉口。一个路段的交通流量与其附近交叉口各个方向的交通流量密切相关。此外，城市道路的交通流量与人们的出行选择有关。户外天气如温度、风速和晴雨等对于人们的出行选择均具有明显影响。

本文在数据层面将根据市区城市道路的特点，收集目标路段附近交叉口各个方向的车流量，将目标路段的天气数据作为影响因素，通过深度分析各类因素与目标路段交通流量的相关性，对天气因素和附近交叉口各个方向的交通流量分模块进行特征挖掘；在算法层面，考虑到数据本身具有周期性的规律，通过嵌入Time2vec提高模型对周期性数据的特征捕捉能力；仿照转轴与齿轮的关系，将输入数据与算法进一步结合，以Bi-GRU模型为基础，从正反2个方向对时间序列信息进行特征挖掘；最后，将Attention机制与Bi-GRU相结合，提高模型的特征学习能力，建立一种融合多因素的“时间齿轮”交通流预测模型。将市区城市道路作为研究对象，与MLP模型、AIRMA模型、SVM模型、RNN模型、LSTM模型、GRU模型和Bi-GRU模型等多种现有模型进行对比，研究预测准确度和预测速度。

1 研究数据及多元因素分析

1.1 交通流数据预处理

目标路段的研究数据源自山东省青岛市即墨区城间公路。使用电子警察采集目标路段(north)及其最近一个交叉路口各方向的交通流量信息，采集时间跨度为8 d，采集周期为5 min。

对原始数据进行检查和清洗。为了弥补缺失的值，采用附近2个数的平均值作为填补。设置有效数据区间，将超出的异常数据使用整体数据的平均值替代，每个方向包含2 304条交通流量数据。目标路段(north)及其最近一个交叉路口各方向的交通流量走势如图1所示。

图1 交通流量走势

1.2 城市道路交通流量分析

城市道路中路段的交通流量与附近交叉口有紧密关系，通过路段中某一横截面的车流量受到邻近交叉口各个方向交通流量的影响。因此，采集目标路段最近的一个交叉口各方向的数据进行研究，可分析各个方向车流量之间的相互影响作用。如图2所示，目标路段的方向为南向北，采用检测器收集其余各个方向路段的交通流量信息，根据皮尔逊相关系数法，可分析各个方向交通流量之间的相关性。二维变量的皮尔逊相关系数如式(1)所示。

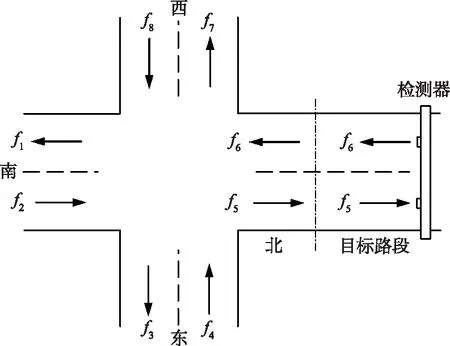
图2 目标路段及最近交叉路口

(1)

图3所示为各个方向交通流量之间的相关性热力图，通常情况下，该系数超过0.8被视为2个因素的相关性较强，处于0.5～0.8之间则被视为2个因素的相关性中等。目标路段为南向北(north)方向，可以看到其余方向的交通流量与north方向的相关性均在中等以上，平均相关系数为0.82，属于强相关。上述结果表明，交叉口各个方向的交通流量对目标路段的交通流量具有显著影响，因此考虑将各个方向的交通流量作为预测模型的输入因素之一。交叉口相关因素部分的输入变量为[f1+f2,f3+f4,f5+f6,f7+f8]，预测模型的最终输出为[f5+f6]。

图3 4个方向交通流量之间的相关性热力图

1.3 出行天气分析

人们的出行常会受到天气因素的影响。青岛气候较为潮湿，且大风天气居多，户外出行通常会考虑温度、风速和阴晴雨等。根据这一特点，本文采用从WunderGround平台获取的天气数据，数据类别包括风速、温度、湿度、气压和阴晴雨，天气数据样本如表1所示。

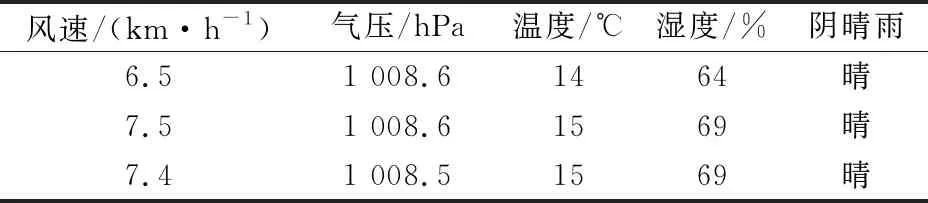
表1 天气因素数据样本

为了体现天气因素对交通出行的影响，本文提出一种更为深度的分析方法，采用K-means聚类算法[22]分析风速和温度对交通出行的影响。K-means聚类方法可以把样本点的特征矩阵区分为n个无交集的簇。首先，设定n个随机的最初质心，通过计算将样本点聚合到位置最为接近的质心，生成簇；其次，计算每个簇中样本点的平均值，将结果作为修正质心；最后，比较修正质心和最初的质心是否一致，如果不一致则再循环上述计算过程，如果一致则停止迭代完成聚类。聚类过程中需要计算的质心距离使用欧式距离，本文使用的三维空间欧式距离公式如式(2)所示：

(2)

式中：xi,yi,zi为样本点的三维特征值；xμ,yμ,zμ为最近质心的三维特征值。

图4所示为温度、风速和交通流量的聚类结果，将聚类的类别设置为3。由图4可知，图中的样本点大致分为3种情况。第1种情况，交通流量较少的绿色点集，多分布在风速高且气温低的区域；第2种情况，交通流量中等的紫色点集，相比第1种情况，分布在风速更为缓和且气温相对舒适的区域；第3种情况，交通流量较高的黄色点集，分布在温度舒适且风速较低的区域。根据这3种情况可以明显看出，人们会相应减少低温和大风天气的出行，而更多倾向于在温度适宜且风速温和的天气下出行。因此，天气变化会明显影响城市道路的车流量。

图4 温度、风速和交通流量的聚类结果

此外，分别计算晴天、阴天和雨天的交通流量平均值，如图5所示，可以看出，晴天的交通流量平均值明显要高于阴天和雨天。可见，人们较多选择晴天出行，减少雨天出行的几率。

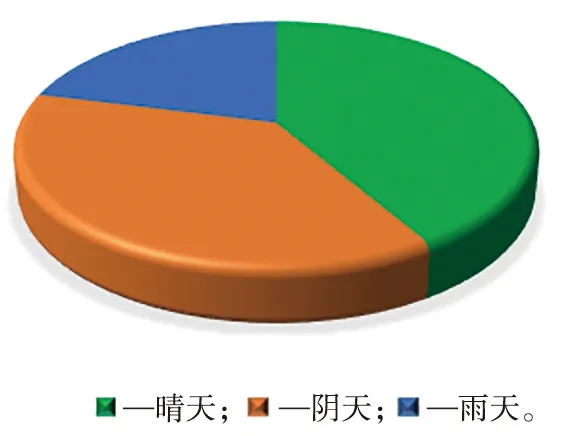
图5 晴天、阴天和雨天的交通流量

综合上述分析可知，为了提高交通流量预测的准确度，需引入更多相关因素作为影响因子。本文选择将风速、温度、湿度、气压和阴晴雨作为天气因素的输入值。

2 TGM预测模型的构建

为了有效协调多种因素对预测模型结果的影响，延长交通流预测的时长，本文建立一种新型的“时间齿轮”预测模型(TGM)。模型内部分为2个模块，模块1对天气因素进行特征提取，模块2对目标路段附近交叉口各方向的交通流量信息进行特征挖掘。最后，将2组模块的输出经过张量拼接输入到多层感知机(multiple perception,MLP)中再次挖掘数据的深层特征。

2.1 提取天气因素

如图6所示，TGM模型的模块1对天气数据进行特征提取。首先，对晴天、阴天和雨天进行热编码，对应值为晴天—2，阴天—1，雨天—0；其次，为了减少不同数据数值范围对预测结果影响的差异，对5种因素进行归一化处理，将数据压缩到0～1之间；最后，使用MLP对天气因素进行特征挖掘，设置2组全连接层(Dense)，单元数设置为128，激活函数设置为relu。

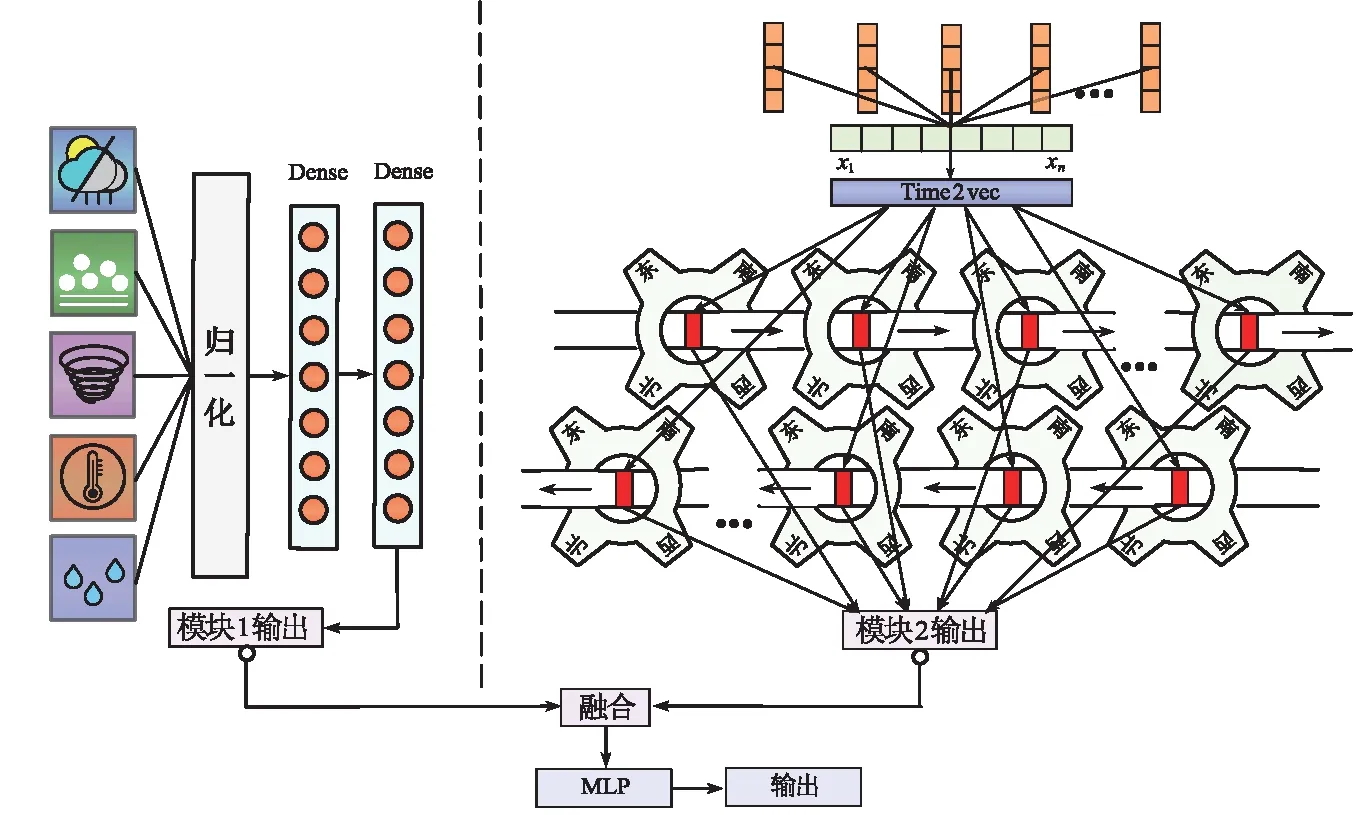
图6 TGM模型的整体结构

2.2 构建时间齿轮模型

交叉路口4个方向的交通流量数据会随着时间变化，而时间信息和各个方向的交通流信息明显在不同的维度。为了更好地体现这种时空特征，本文仿照转轴与齿轮的关系，将时间线抽象为齿轮的转轴，4个方向的交通量数据则在齿轮的轮齿上。如图6所示，每一个时间点xn均包含4个方向的交通流量数据，并将4个方向的数据排布在轮齿上沿着时间转轴传递信息。本文设置2组时间齿轮，根据正向和反向的时间线综合提取交通流的时空特征。

如同齿轮的周期性运动，交通流数据也具有明显的周期性。为了增强模型对时间序列数据的特征捕捉能力，使用一种基于Time2vec的时序数据表征学习方法[23]。在方法中添加一个正弦函数，使模型能够更容易地捕获到交通流数据的隐藏周期变化规律。如图6所示，将Time2vec嵌入到预测模型中。Time2vec的公式如式(3)所示：

(3)

式中：x为原始时间序列的特征；α和β分别为三角函数中可学习的频率和相位；ε为第ε个特征；w为特征维度。

为了充分学习交通流数据的时间特征，对TGM模型的算法框架在Bi-GRU网络的基础上进行改进。与LSTM相比，GRU在确保一定精度的同时，还进一步简化了内部组成。GRU内部组成如图7所示。

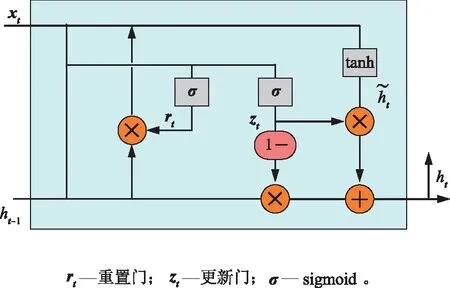
图7 GRU结构

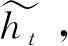
如图8所示，Bi-GRU网络将时序数据按照2个相反的方向分别送入到2组GRU中，再将2组输出的结果进行融合，因此模型的输出考虑到了未来数据信息对历史数据信息的影响，这种结构在大量学术研究中被证明具有更优的模型性能[24]。本文使用多维时空数据，Bi-GRU尽管具有优越性能，但是在数据复杂的情况下，模型为了充分挖掘数据的特征会增加迭代次数，变得难以拟合。因为传统神经网络的学习过程通常会兼顾全局信息，模型需要对信息进行逐个分析，因而大大增加了模型的学习成本。可见，面对多维度且大量的数据，如果重点分析其中的关键信息，并减少非关键信息的关注度，则可以降低模型的学习成本，使模型的计算过程变得简单灵活。

图8 Bi-GRU结构

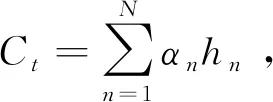
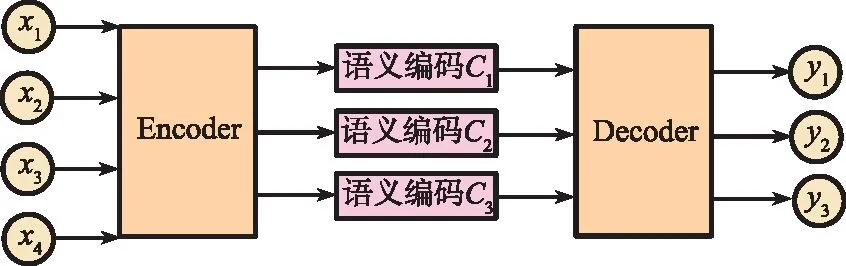
图9 引入Attention机制的Encoder-Decoder结构

综上所述，为了提升Bi-GRU对多维数据的特征提取能力，将注意力机制分别加入到正向GRU和反向GRU中，同时对Attention机制进行改进，可提高特征权重对GRU最终信息提取结果的依赖性。加入改进Attention机制的Bi-GRU结构如图10所示。

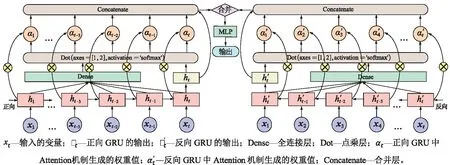
图10 结合改进Attention机制的Bi-GRU

如图10所示，对Bi-GRU的正向和反向加入改进的Attention机制。在正向和反向的GRU中，输入值xt经过GRU信息深层挖掘，获得相应的信息提取结果，分别将正向GRU和反向GRU信息的最后一个结果ht和ht′单独提取出来。然后，将每一个GRU单元的信息提取结果送入Dense层，按照输入参数的维度标准化，将正向计算结果和反向计算结果分别设为[d1,d2,d3,…，dt]和[d1′,d2′,d3′,…，dt′]。为提升Attention机制计算权重值对GRU最终信息提取结果的依赖，将Dense层的计算结果和ht，ht′进行点乘，并使用激活函数softmax将计算结果转换为衡量信息重要性的权重分数，将正向和反向Attention机制计算的权重设为A和A′。计算过程如式(4)和式(5)所示：

A=softmax([d1,d2,d3,…,dt]·ht)=[α1,α2,α3,…,αt]，

(4)

A′=softmax([d1′,d2′,d3′,…,dt′]·ht′)=[α1′,α2′,α3′,…,αt′]。

(5)

通过权重分配机制，提高模型对重点信息的关注度。将计算出的权重值和GRU每个单元信息提取值的对应元素相乘并求和，正向和反向的计算过程如式(6)和式(7)所示：

(6)

(7)

考虑到GRU最终信息提取结果较为重要，将权重求和的结果和GRU最终信息提取结果合并，结合Attention机制的正向GRU输出特征矩阵为Y1=[C，ht]，结合Attention机制的反向GRU输出特征矩阵为Y2=[C′，ht′]。通过上述计算过程，将改进的Attention机制加入到正向GRU和反向GRU中，最终的输出结果为Y=[Y1，Y2]，再添加MLP层进一步挖掘信息的深层次特征。

3 结果验证与分析

3.1 相关设置

本文设置多个对比模型，预测未来5，15，25 min的交通流量。训练集和验证集的比例设置为7∶1，输入步长为24(120 min)，学习率为0.000 1，一次性的投放抓取次数设置为128。将MSE作为模型的损失函数，使用Adam作为模型优化器，轮数epoch设置为300，Time2vec的特征数设置为64，TGM模型中Bi-GRU2个方向的神经元数均设置为64，激活函数使用tanh。

3.2 多因素对比结果

为了证明多因素预测模型及算法改进的优越性，进行以TGM模型为基础的消融实验，具体的参照对象设置如下：

上述研究中，研究组溃疡消失时间（37.20±11.52）d、症状缓解时间（14.13±5.26）d与幽门螺杆菌转阴时间（23.08±2.49）d均低于对照组，研究组治疗后经胃镜检查结果痊愈率为88.33%，与对照组（68.33%）比较，组间比较，差异具有统计学意义（P＜0.05），由此可见，在抗幽门螺杆菌的含铋四联疗法上加用双歧杆菌四联活菌片治疗消化性溃疡的效果显著。

TGM-Weather：在TGM模型的基础上，去除天气因素提取模块；

TGM-Space：在TGM模型的基础上，输入值去除其余方向路段的交通流数据；

TGM-Attention：在TGM模型的基础上，去除Attention机制，算法框架使用Bi-GRU；

TGM-RNN：在TGM模型的基础上，保留Attention机制，将Bi-GRU换成RNN。

上述参照模型以及TGM模型的预测结果如图11所示。

图11 预测结果对比

由图11可以看到TGM模型的预测性能相比其他对照模型具有明显提高。消融实验表明，当模型分别加入了天气因素、附近交叉口交通流量因素、Attention机制和Bi-GRU后，5，15，25 min的交通流预测准确度均有相应提升。与不考虑交叉口和天气因素的模型相比，TGM模型结合城市交通的特点，能够更好地捕捉城市路段交通流量的特征。此外，在TGM-Attention模型和TGM-RNN模型中可以看到，Attention机制和Bi-GRU对预测结果具有明显的影响。以上实验证明了融合天气因素和最近交叉口各方向路段交通流量信息，以及仿照转轴与齿轮关系建立TGM模型进行交通流预测的合理性。

3.3 预测模型对比分析

为了证明TGM模型具有更为准确的交通流预测能力，将MLP模型、AIRMA模型、SVM模型、RNN模型、LSTM模型、GRU模型和Bi-GRU模型设置为对比实验模型，所有对比模型的相关参数与TGM模型保持一致，并将模型的性能调至最佳状态。对比实验的预测结果见表2和表3。

表2 实验结果：MAE对比

表3 实验结果：RMSE对比

从表2和表3中可以看出，与其他模型相比，TGM模型具有更佳的预测效果。TGM模型预测5，15，25 min交通流的MAE值分别为5.21，5.73和6.24，RMSE值分别为7.22，8.29和8.79。当预测时间延长时，TGM模型在15 min和25 min实验组的预测误差MAE相比5 min实验组分别增加了9.08%和16.51%，RMSE相比5 min实验组分别增加了12.91%和17.86%。可见，TGM模型能够在预测时间延长的同时保证误差在合理范围内，具有稳定的中长时预测能力。

在15 min和25 min实验组中，传统机器学习算法的预测误差增加幅度较大。相比5 min实验组，MLP，AIRMA和SVM的15 min预测误差MAE值分别增加了18.19%，18.23%和13.24%，25 min预测误差MAE值分别增加了26.28%，25.30%和24.41%。可见，传统机器学习算法的中长时预测不稳定。在15 min实验组中，与RNN，LSTM，GRU和Bi-GRU相比，5 min实验组的预测误差MAE值分别增加了16.88%，14.35%，10.83%和10.62%。在25 min实验组中，与RNN，LSTM，GRU和Bi-GRU相比，5 min实验组的预测误差MAE值分别增加了29.72%，27.28%，25.26%和18.24%。典型循环神经网络模型和Bi-GRU模型在中长时预测实验中，其误差增加幅度均比TGM模型大，说明TGM模型相比其他模型在中长时预测方面更加稳定。此外，TGM模型预测15 min和25 min的误差MAE值相比性能较优的Bi-GRU模型分别降低了6.37%和6.73%，RMSE值分别降低了7.09%和7.99%。结果表明，TGM模型相比其他模型在预测准确度方面提升也明显。

图12所示为TGM模型预测值与实际交通流量的对比曲线图。

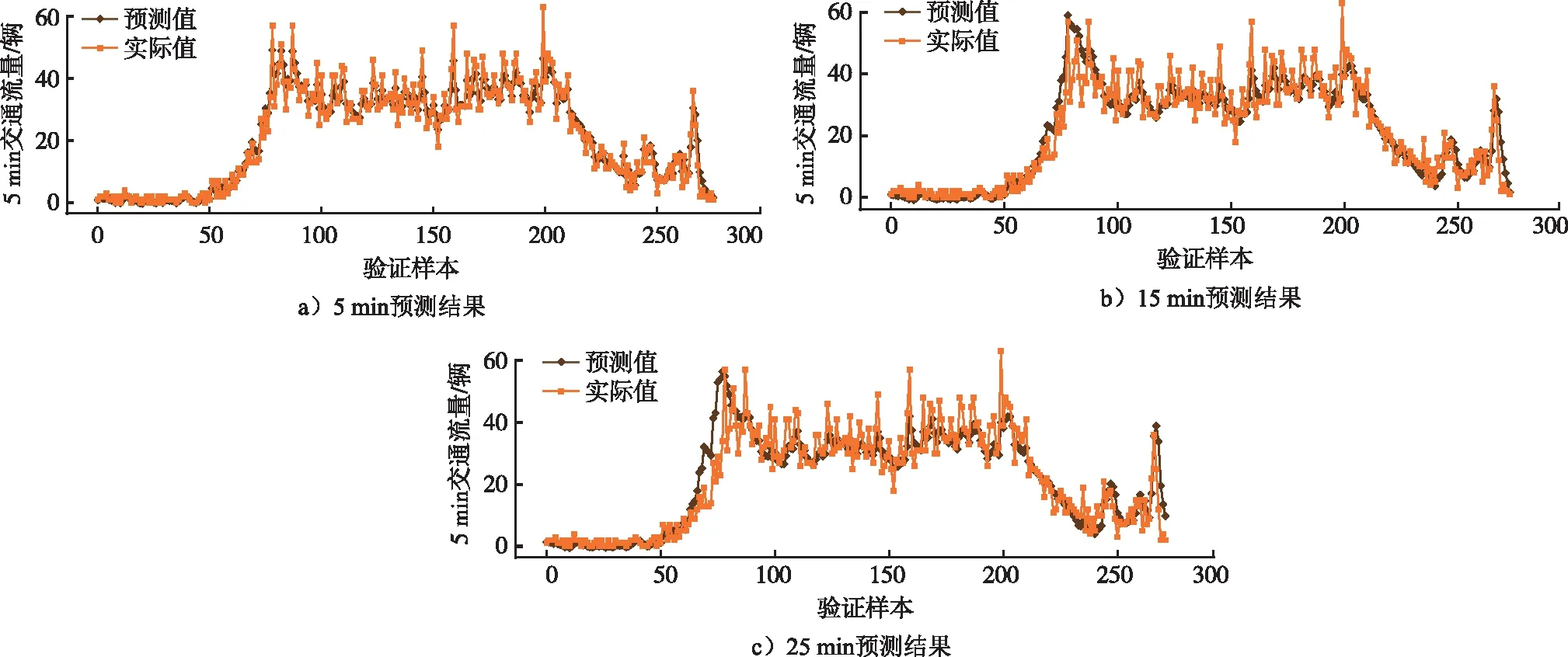
图12 TGM模型预测结果与实际值对比

由图12可知，TGM模型很好地预测了实际交通流的变化趋势，并且在多处曲线峰值处与实际值高度重合。此外，TGM模型在中长时交通流预测方面仍具有可观的拟合效果，进一步验证了TGM模型的优越性。

4 结 语

1)提出了一种融合多因素的“时间齿轮”交通流预测模型，深度分析了天气因素和邻近交叉路口各方向交通流量对目标路段交通流量的影响，融合多因素对交通流进行预测。

2)提出的TGM模型分为2个模块，模块1使用MLP对天气因素进行信息提取，模块2仿照转轴和齿轮结构，将时间线和交叉路口各方向交通流量抽象为转轴与齿轮，参照齿轮的旋转周期，嵌入Time2vec提升模型对数据周期性规律的学习能力，再将模块1和模块2的结果合并，添加MLP得到最终输出的预测结果。消融实验验证了所提出的TGM模型在方法上具有合理性。

3)与MLP模型、AIRMA模型、SVM模型、RNN模型、LSTM模型、GRU模型和Bi-GRU模型对比可知，TGM模型具有更强的非线性拟合能力和更高的预测准确度。相比性能较优的Bi-GRU模型，TGM模型在预测15，25 min交通流量的结果中，MAE值分别降低了6.37%和6.73%，RMSE值分别降低了7.09%和7.99%，可以满足中长时预测精度的要求，为交通协调管理控制提供数据支撑。

4)本文提出的TGM预测模型仅针对城市公路，面对复杂多变的道路交通情况，其预测性能仍有提升空间。未来将考虑增加出行兴趣地点和行车轨迹等因素，并区分私有车辆和公有车辆，进行更为深入的交通流预测研究。