基于模糊聚类的多类簇归属电力实体行为异常检测算法
郭禹伶,左晓军,崔景洋,王 颖,张光华
(1.国网河北省电力有限公司电力科学研究院,河北石家庄 050021;2.河北科技大学信息科学与工程学院,河北石家庄 050018)
随着数字化主动电网的建设与发展,电力设备信息化、数字化和智能化水平进一步提高,物理设备和信息系统耦合加剧,紧密耦合给配电设备和电力网络带来了更大的体系结构风险和更高的网络安全隐患[1]。主动电网中的电力实体呈现出明显的离散化、开放化、差异化特征,而逐步模糊的网络边界发展趋势使得主动电网面临的网络安全威胁剧增。主动电网中分布的实体种类丰富多样,包括用户设备与电力设施设备,这些实体在提升电网运行效能的同时也带来了新的安全威胁,主动电网的安全形势变得更加复杂[2]。对各类电力实体进行研究,分析其异常行为趋势[3]可以发现未知网络安全风险,提高数字化主动电网的网络安全防护能力。
电力实体一般包括电网内的各类信息系统、网络安全防护装置、主机设备等,其异常检测问题属于用户与实体行为分析(user and entity behavior analytics,UEBA)范畴[4],电力实体行为异常检测的主要目的是检测主动电网的内外部网络安全威胁,进一步提高主动电网的网络安全防护能力。在外部威胁识别方面,PAN等[5]设计了一个动态行为残差生成器,通过实体行为分析过滤装置对多种攻击方法进行检测,解决了静态检测模型异常检测种类少的问题。也有学者基于长短期记忆网络(long short-term memory,LSTM)及深度自编码器(deep auto encoder,DAE)建立了专门针对电网传输系统的异常检测模型[6],该模型能够对传感器实体数据进行分析,从而监控传输保护系统和检测恶意活动。在内部威胁识别方面,JIN等[7]基于统计学习方法对智能电表数据进行分析,对电力高阶消耗数据在电网中潜在的电力盗窃行为进行分析,识别其中的盗窃者与受害者。李佳玮等[8]通过对电力工控系统数据在时间维度上的周期性进行分析,建立了基于高斯混合聚类的时序异常检测模型,通过层次聚类的方式解决异常检测问题。
但上述异常检测方法都对待测样本进行“硬划分”,每个样本只归属于一个类,异常检测结果只与样本所属类簇内的样本有关,缺乏其他类簇内的样本对比,而实际情况中,电力实体行为既有“伪装性”,又有“复杂性”,不应只在一个类簇内进行分析[9]。模糊聚类[10]采用模糊数学方法对数据进行分析,最终得到样本类别隶属度矩阵,一个样本可能同时属于多个类别。基于模糊聚类算法处理电力实体行为数据,能够很好地保留样本与各个类簇间的关联信息,通过多角度评估判断电力实体的威胁程度,得到更准确的异常检测结果。ANGELOS等[11]使用模糊C均值聚类对用户用电数据进行分析,随后,基于样本对应每个类别的隶属度和类别中心的欧式距离设计了一种评价指标,用于区分不同的用电模式,从而得到其中的欺诈者。文献[12]利用模糊聚类对用电数据进行分析。首先,将具有相同用电习惯的电力用户进行聚类;然后,使用孤立森林算法对其中的用电异常情况进行检测,得到了不错的检测效果,但在使用模糊聚类结果时,只选择了其中的一个类别作为样本标签,没能很好地体现出算法的“模糊性”。
针对评价角度过少以及样本类别信息使用不完全的问题,本文提出了一种基于模糊聚类的多类簇归属异常行为检测(abnormal behavior detection based on fuzzy clustering,ABDFC)算法,包括模糊聚类以及多类簇异常检测2个过程。首先,基于实体行为频次-逆向实体频次(behavior frequency-inverse entities frequency,BF-IEF)技术建立了实体行为模糊C均值聚类算法,得到样本与类别的隶属度矩阵;其次,针对模糊聚类的结果,利用样本多类簇归属的性质设计了异常检测算法。
1 基于模糊聚类的多类簇归属异常检测算法
本文所提出的电力实体异常检测算法包含2个主要部分:1)实体行为模糊C均值聚类过程;2)多类簇归属异常检测过程。首先,从主动电网中进行电力实体行为的数据采集,并对其进行向量化和标准化操作;其次,通过模糊聚类过程得到模糊聚类结果,再对模糊聚类结果进行多类簇归属异常检测。整体处理框架如图1所示。

图1 总体框架
1.1 实体行为模糊C均值聚类算法
模糊聚类算法采用模糊界限对待测样本进行软划分,通过隶属度对样本与类别之间的关系进行表述,使得一个样本可以有多个类别标签[13]。模糊C均值(fuzzy c-means,FCM)聚类算法[14]是模糊聚类算法中最具代表性的算法之一,其通过多次迭代的方式计算样本关于类别的归属度与聚类簇中心点,以达到最大类内相似度与最小类间相似度。模糊C均值算法是对普通K均值(K-means)算法的一种改进,为了便于与K均值算法进行区分,所以改用字母C代表聚类簇的个数。传统FCM算法主要使用欧式距离对样本与类别中心的偏离程度进行度量,在电力实体行为模糊聚类分析的过程中,发现直接计算行为向量间的距离对具体实体行为的区分度不理想,所以基于TF-IDF思想优化了实体行为处理方法,设计了实体行为模糊C均值聚类(fuzzy c-means for entities behavior,FCEB)算法。
TF-IDF[15]是文本分析领域的一种语料库词语加权技术,用来评估一个单词对整篇文档的重要程度。其主要思想是:一个单词在整篇文档中的重要程度与其出现的频率成正比,与其在其他文档中出现的频率成反比。在电力实体行为分析中,参考TF-IDF对电力实体的具体行为进行差异化分析,计算实体行为频次-逆向实体频次BF-IEF。
若有某一行为B,则B的实体行为频次BF计算方法为
(1)
实体行为频次BF为某个行为出现次数与行为数量的比值,一个行为在某个实体的所有动作中出现的次数越多,越能代表该实体,而且越能够区分该实体与其他实体的差别。
行为B的逆向实体频次IEF计算方法为
(2)
式中:逆向实体频次IEF为电力实体总数量与包含某个行为实体数量比值的对数,对数内的分母进行加1,是为了防止出现分母为0的情况。如果一个行为只在少数实体中出现,则能够更好地区分这些实体与其他实体的不同。出现的范围越广,那么这个行为的区分性就越差。
实体的频次与逆向实体频次的乘积为
BF-IEF=BF×IEF 。
(3)
将BF与IEF相乘可以得到实体行为频次-逆向实体频次,该表述方法能够很好地对实体间的行为差异程度进行区别,实体某个行为的表述能力随着它在该实体行为中出现次数的增加而增加,随着它在其他实体内出现次数的增加而减少。使用BF-IEF技术对行为进行处理,可以更精确地表述实体行为向量,增强行为表示的准确性。
基于实体行为向量表述方法,再给定第i个数据样本xi与第j个聚类类别中心vj,即可计算数据样本与聚类类别中心的距离。二者之间的行为向量相似性度量值(behavioral measure,BM)的计算方法如式(4)所示:
(4)
基于实体行为向量表述方法与实体行为向量相似性度量方法,可以构造实体行为模糊C均值聚类算法。在模糊聚类中,使用隶属度表示一个样本x对于某个类别c的隶属程度,一般记为uij。uij表示第i个样本对于第j个类别的隶属度,其取值范围是[0,1]。当uij=0时,表示第i个样本一定不属于第j个类别;当uij=1时,表示第i个样本一定属于第j个类别。
基于隶属度可得到模糊聚类的目标函数,假设数据集X={x1,x2,…,xN},聚类类别C={C1,C2,…,CC},第j个聚类类别中心vj,则实体行为模糊C均值聚类FCEB算法的目标函数如式(5)所示:
(5)
满足
(6)
式(5)中:m是模糊系数,取值范围 [1,+∞),用来调节聚类模糊程度的参数,m值越大,聚类结果越模糊,一般取m=2。式(6)表示某个样本到所有类簇中心的隶属度之和为1。
利用拉格朗日乘数法,引入N个拉格朗日因子将式(5)与式(6)转化为无条件极值问题:
(7)
对式(7)中的uij与vj进行求导,可以得到各变量的极值点。
对隶属度参数uij求偏导得:
(8)
对聚类簇中心vj求偏导得:
(9)
式(8)是隶属度迭代公式,式(9)是聚类簇中心迭代公式。
所以实体行为模糊C均值聚类FCEB算法的步骤如下。
1)初始化C个样本作为初始聚类中心C={C1,C2,…,CC},第j个聚类类别中心vj。
2)针对每个样本xi,计算它到第j个聚类中心的距离,并更新隶属度矩阵:
(10)
3)针对每个类别,重新计算它的聚类中心
(11)
4)重复第2、第3步,直至达到最大迭代次数或者隶属度矩阵变化小于阈值。
1.2 多类簇归属异常检测
随着网络技术的不断发展,电力实体行为中的异常情况呈现出明显的复杂化、隐蔽化特征[16]。现有异常检测算法多基于单一维度对行为内容进行分析,采用传统方法对模糊聚类结果进行异常检测,会丧失模糊聚类结果的“模糊”特性。局部异常因子(local outlier factor,LOF)算法[17]是一种常见的基于密度的单维度异常检测算法,通过比较待分析节点与邻居节点之间局部离群值的大小,从而判断待分析节点是否异常。本文基于LOF算法,设计了一种多类簇归属的异常检测(anomaly fetection based on multi-categories affiliation,ADMA)算法专门用于解决模糊聚类结果的异常检测问题。
在同一类簇内所有的数据点中,距离待分析点O最近的第k个点与点O之间的距离被称为K近邻距离[18],用K-nearest neighbor distances表示,如图2所示。点O的K近邻距离越大,则其周围的点越稀疏,越远离主流数据分布。
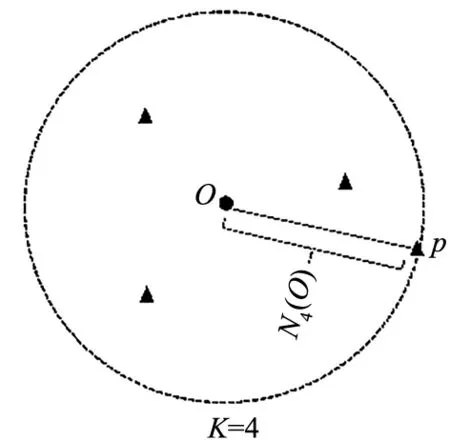
图2 点O的K近邻距离
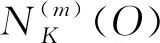

图3 点O在不同类簇内的K近邻距离
点p到点O间的可达距离(reach_dist)定义为“点O的K近邻距离”和“数据点p与点O直接距离”的最大值,即:
reach_dist(p,O)=max{KNND(O),dist(p,O)}
(12)
值得注意的是,式(12)的定义是有方向的,点p到点O的可达距离可能不等于点O到点p的可达距离。
点O的近邻密度(nearest neighbor density,NND)用来衡量点O在所属的聚类簇内与周围其他点相比的疏密程度,定义为每个类簇内K邻域内的点与点O平均可达距离的倒数,即:
(13)
式中:m代表第m个簇,对每个点O的归属聚类簇进行计算,可以得到M个点O的近邻密度。平均距离越低,近邻密度越高,近邻密度高意味着该点附近比较稠密。另外,在点O的邻域内,可能不止包含K个点,所以要根据实际情况归一化可达距离之和,图4是当K=4时,点O的4邻域内包含6个点的情况。
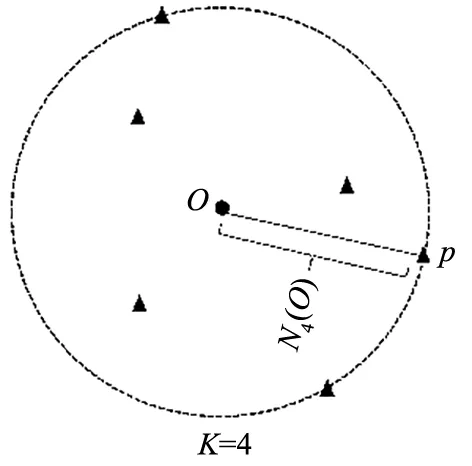
图4 点O的K近邻内包含多个点的情况
在ADMA算法中,使用点O近邻相对异常因子(nearest neighbor relative anomaly factor,NNRAF)对点O的异常程度进行衡量,其异常因子得分为点O在M个类簇邻域内样本点的平均近邻密度与点O近邻密度之比的平均值,即:
(14)
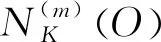
1.3 ABDFC异常检测算法过程
基于实体行为模糊C均值聚类(FCEB)与多类簇归属异常检测(ADMA)算法,设计了一种基于模糊聚类的多类簇归属异常检测ABDFC算法。首先,采用BF-IEF技术对电力实体行为进行处理;其次,采用多次迭代的方式得到各实体行为的模糊聚类结果;最后,根据类簇隶属度矩阵对异常行为进行识别。算法的整体过程主要包括模糊聚类和多类簇归属异常检测2个阶段,算法流程如图5所示。

图5 ABDFC算法流程图
具体步骤如下:
1)标准化现有实体行为信息数据集X={x1,x2,…,xN};
2)设定模糊聚类超参数(类别个数C与模糊系数m);
3)初始化聚类中心,设第j个聚类类别中心vj;
4)针对每个样本xi,利用它到第j个聚类中心vj的距离计算uij,并更新隶属度矩阵:
(15)
5)针对每个类别,重新计算它的聚类中心vj:
(16)
6)重复第4、第5步,直至达到最大迭代次数或者隶属度矩阵变化小于阈值,最终得到隶属度矩阵;
7)遍历数据集X内的样本,根据每个类别的隶属度计算其NNRAF值,并判断是否为异常点。
(17)
2 实验仿真
2.1 数据来源
为了验证异常检测算法的有效性,本文通过散布在主动电网重要节点中的网络探针得到了变压器、传感器、智能电表等各类物联网电力实体间的通信数据,部分原始数据样例如下所示:
“Source IP,Destination IP,25950,2021/8/13 18:53:06,tcp,private,RSTR,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,2,2,0.00,0.00,1.00,1.00,1.00,0.00,0.00,255,2,0.01,0.69,1.00,0.00,0.00,0.00,1.00,1.00
Source IP,Destination IP,1,2021/8/13 18:53:08,tcp,smtp,SF,1079,334,0,0,0,0,0,1,0,0,0,0,1,0,0,0,0,0,1,1,0.00,0.00,0.00,0.00,1.00,0.00,0.00,138,167,0.57,0.03,0.01,0.01,0.00,0.00,0.00,0.00”。
基于参考文献[4]中的特征工程方法和NSL-KDD[19]的数据格式对电力实体间的通信数据进行了标准化预处理,经过处理后的每条连接共有43个特征,部分特征如表1所示。
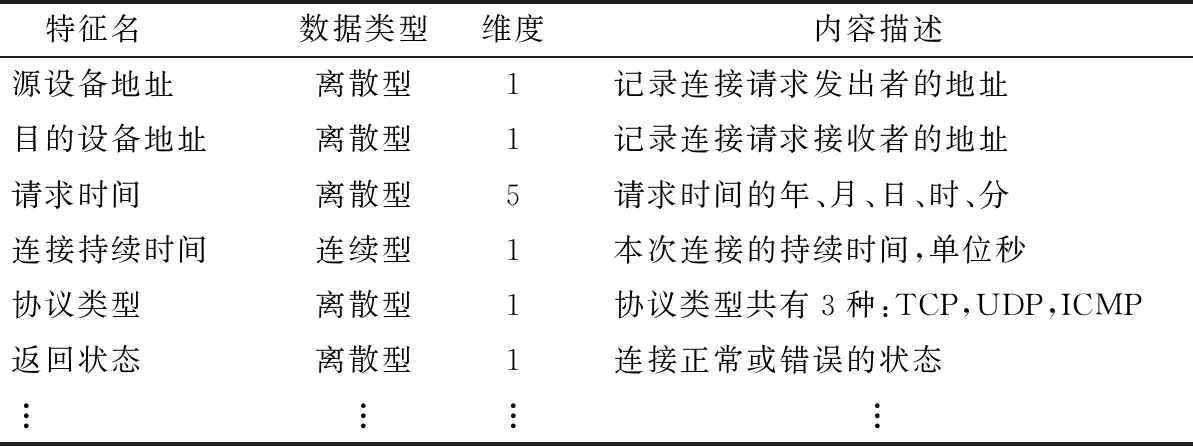
表1 电力实体行为数据特征样例
除了1.3节中所表述的BF-IEF加权技术,还使用归一化过程对数据进行特征缩放,经过处理后的数据压缩到0到1之间,其归一化方法为
(18)
另外根据NSL-KDD的攻击判断逻辑对样本数据进行了类别标注,并补充了部分攻击数据,最终得到5大类、39小类共1 000条电力实体通信行为数据,数据分布情况如表2所示。
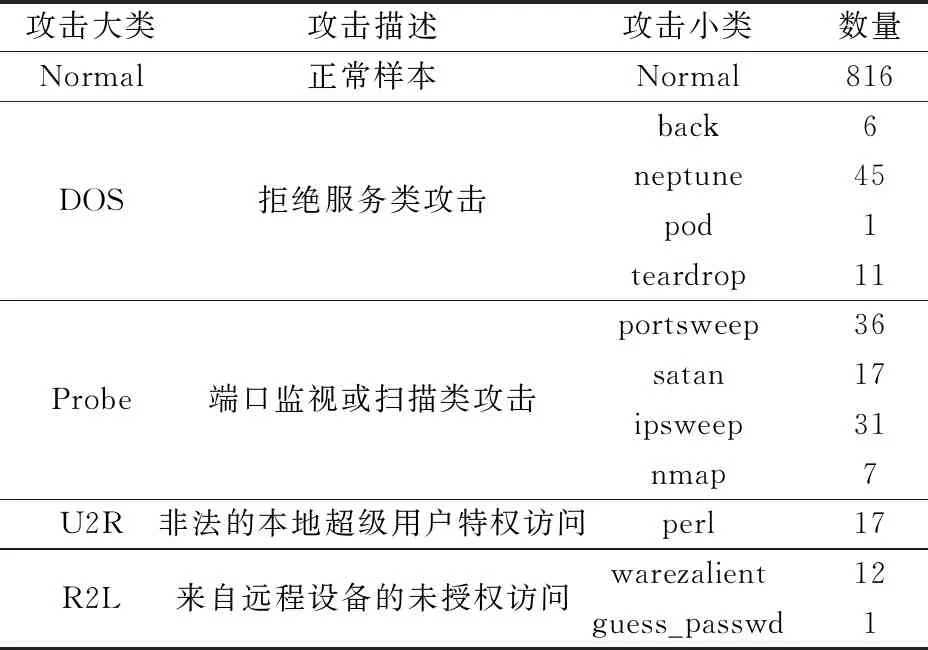
表2 实验数据的类别分布情况
2.2 评价指标
在对算法评价的过程中,基于混淆矩阵[20]对各类指标进行计算,混淆矩阵如表3所示。

表3 混淆矩阵
其中TP(true positive)代表真正例,是正样本被预测为正样本;FP(false positive)代表假正例,是负样本被预测为正样本;FN(false negative)代表假负例,是正样本被预测为负样本;TN(true negative)代表真负例,是负样本被预测为负样本。基于混淆矩阵可以得到若干评估指标,常用的指标有准确率(accuracy,Acc)、精确率(precision,P)、召回率(recall,R)和F1值,具体的计算方法如下所示。
(19)
(20)
(21)
(22)
此外还使用了受试者工作特征曲线(receiver operating characteristic curve,ROC)和ROC曲线下的面积(area under curve,AUC)对算法进行评价。
3 结果与分析
本次实验在Intel core i7-9750H@2.6 GHz处理器,16G内存,Python 3.7.2环境下运行。多分类实验的识别结果按照攻击大类进行统计,分别是Normal,DOS,Probe,U2R,R2L。
首先,进行模糊聚类分析。在参数选择方面,模糊聚类超参数m设置为2,C值设置为5。图6中,随机选取了3个样本维度进行展示,将其隶属度最大的一类作为最终类别。由图6可以看出,整体数据的模糊聚类情况有一定的分布规律,Normal类分布在xy轴平面,主要集中在x轴、y轴及对角线上;Probe类多分布在y轴;其余3类多集中在原点附近。
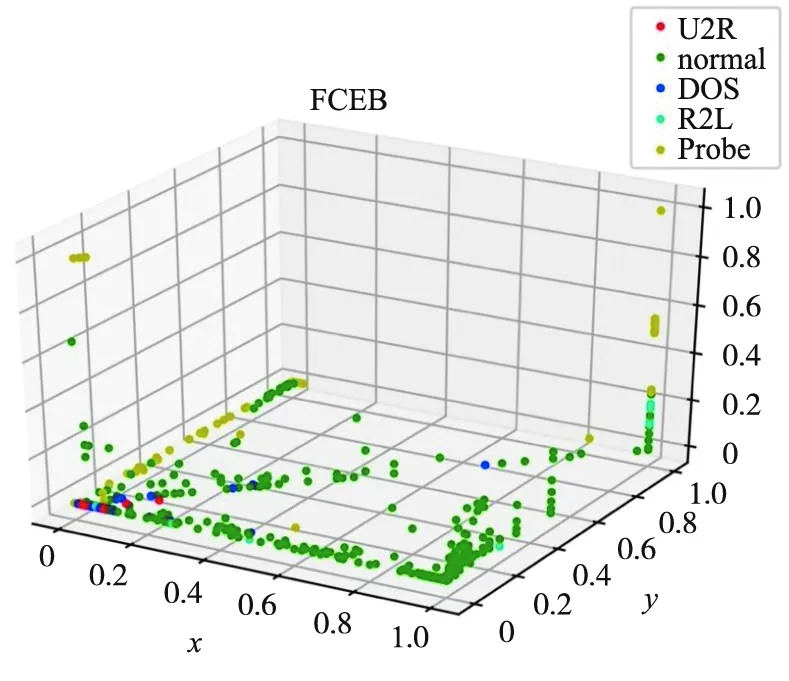
图6 实体行为模糊C均值聚类结果
选取了LOF,K-Means,Random Forest与本文所提出的ABDFC算法进行异常检测效果对比,结果如图7所示。在异常行为检出量方面,本文提出算法所检出的异常行为最多,在1 000个样本中,共识别得到了非Normal类数据164条。
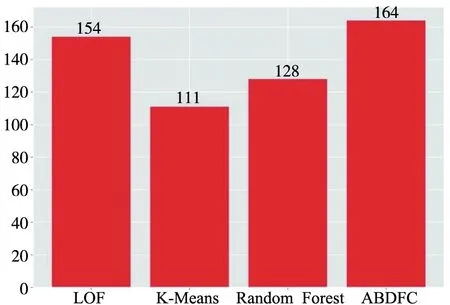
图7 异常检出量对比
算法的多类别检测将数据集按照类别进行拆分后再进行实验。表4是4种算法在多类别数据上的评价指标,由表4可以看出ABDFC算法整体表现最优,随机森林略弱。ABDFC算法在R2L类别与Probe类别的检测方面稍有不足,Random Forest在这2个类别检测的各个指标上均表现最好。虽然ABDFC算法在多个类别的检测上均取得了不错的效果,但由于R2L类别样本数较少,所以模型未能很好地从数据中学习到相应的规律,影响了ABDFC算法评价指标的平均值。

表4 评价指标对比
图8分别给出了4种算法在进行多类别检测任务时的ROC。由图8可以看出ABDFC算法的ROC曲线下面积在全量异常识别、Normal类识别、DOS类识别实验中性能优势较为明显,ROC分别达到了0.86,0.84和0.83。由于其他3个类别的样本数量较少,所以检测效果略有波动。

图8 不同算法ROC曲线对比
从图8各子图的ROC曲线来看,ABDFC算法在全量数据集的异常检测实验中表现最好,其ROC远大于其他算法,这是由于在全量数据集中实体行为种类更多,基于BF-IEF技术所改进的模糊聚类能够对各类电力实体的行为进行更好的区分,从而得到更优的模糊聚类效果。而且在分类别异常检测试验中,实体类别的多样性有所降低,ABDFC算法在多类簇归属信息使用方面的优势有所下降,所以呈现出的检测优势不如全量数据集异常检测试验中大。与传统LOF算法相比,经过电力实体样本多类簇归属性质改进的ABDFC算法进行了更多维度的异常因子计算,可以检测出更多的异常点,对比LOF算法有着更优的表现。Random Forest算法在各个异常检测的实验中对数据的大小变化不敏感,表现比较稳定,但从ROC来看稍逊于ABDFC算法。
此外,还对ABDFC算法的实时识别能力进行了测试,如表5所示。由表5可知,ABDFC算法在进行小批量在线检测方面也优于其他算法,适合作为实体行为增量检测模型进行全天候部署检测。

表5 小批量检测准确率对比
从实验结果上看,ABDFC算法对于电力实体行为异常检测的整体表现优于LOF,K-Means及Random Forest算法,尤其在Normal样本检测方面的各类指标都比较突出。在实际应用中,电力实体行为分析的主要作用在于对数据进行“正常”与“异常”的二分类验证,所以ABDFC算法比其他3种算法更适用于当前电力实体行为的异常检测。
4 结 语
本文提出了一种基于模糊聚类和多类簇归属的异常检测算法,主要应用于电力实体行为分析。首先,基于行为度量方法设计了实体行为模糊聚类算法,并得到电力实体行为与类别间的隶属度矩阵,解决了确定性聚类算法分析角度单一的问题。其次,基于隶属度矩阵设计了多类簇归属异常检测算法,对电力实体行为在各个所属类别内的相对结构进行分析,判断该点的异常情况。结果表明,ABDFC算法解决了传统异常检测算法实体行为硬划分的问题,通过在不同类内分别计算异常程度的方式得到更为准确的检测结果。
本文方法虽然能够利用模糊聚类以及多类簇归属异常检测算法对电力实体行为的异常情况进行分析,但在实验过程中所涉及的超参数较多,因此,对超参数的设置过程和具体影响进行研究,设计自动化模糊聚类异常检测算法是下一阶段的研究方向。

