离轴光学系统的畸变分析及焦距测量

程强，胡海翔，李龙响，王孝坤，罗霄，张学军，2

（1.中国科学院 长春光学精密机械与物理研究所中国科学院光学系统先进制造技术重点实验室，吉林 长春 130033；2.中国科学院大学，北京 100049）

1 引言

随着空间光学遥感技术的快速发展，为满足空间对地观测高分辨、大视场的成像需求，离轴光学系统已逐渐成为空间光学遥感器的重要发展趋势。离轴光学系统具有更多的设计自由度，且没有中心遮拦、调制传递函数高等诸多优点，可满足空间光学遥感器对地观测的高分辨率、大幅宽需求［1-4］。

在离轴光学系统的畸变分析及测量方面，北京空间机电研究所针对超宽视场的离轴光学系统开展了全视场畸变的一致性校正技术研究，相关研究成果成功应用于两台超宽视场离轴系统的装调校正，取得了良好的效果［5］；中科院长春光机所针对离轴三反光学系统，开展了镜头像面畸变标定及相机畸变测量等方面的研究及工程实践，并应用于某测绘产品镜头的高精度标定［6-9］，但其鲁棒性不够理想，针对工程实际中的随机误差解算精度和稳定性不足。此外，浙江大学［10］、吉林大学［11］、中科院上海技术物理研究所［12］也对光学系统的畸变分析及测量技术开展了深入研究。

本文介绍的某离轴光学系统，采用时间延迟积分电荷耦合器件（Time Delay Integration Charge Coupled Device，TDICCD）推扫成像，光学系统视场角为0.37°×3.5°，相机最大相对畸变设计值为1.413%。光学系统的畸变将直接影响成像的几何位置精度，对系统的成像定位造成影响。

本文对离轴光学系统的理论畸变进行了分析，提出了等效焦距概念，对离轴光学系统的相对畸变系数进行了分离，并针对装调完成的某离轴光学系统，利用多维约束非线性优化方法完成了畸变分析和焦距测量，对相机实际焦平面上特征点的物像对应关系进行解算，提高了系统畸变及焦距的解算精度和稳定性，为相机在轨图像的快速、高精度畸变校正提供准确输入。

2 反射光学系统的理论畸变

畸变广泛存在于各类光学系统中。光学系统产生畸变的原因是在一对物、像共轭平面上，垂直放大率随视场角的变化而变化，不再保持常量，导致像相对于物失去了相似性。因此，畸变虽然不影响成像的清晰度，却直接影响成像的几何位置精度。

随着光学系统视场角的变大，系统的畸变也随之变大。对于空间光学遥感器而言，其口径和视场一般都比较大，且成像精度要求较高，因此必须采取措施来减小甚至消除畸变带来的影响。

传统的同轴反射光学系统如Ritchey Chretien（R-C）系统，其所有光学镜面都关于系统光轴回转对称，因此对于视场角相同的物点，不论方向如何，其垂轴放大率都是一样的。这种情况下，畸变只与像高有关。像高相同的轴外物点，其径向畸变量是相同的。在像面上，畸变图像关于光学中心呈中心对称。此时随初级畸变系数的不同，畸变分别呈现出枕形畸变和桶形畸变。

而对于离轴反射光学系统，与传统的R-C系统相比，主、三镜离轴放置，不关于光轴对称。因此光学系统的垂轴放大率不但随视场角大小而改变，而且随轴外点的离轴角而变化。对轴外物点成像时，如果它们的主光线方向不同，即使其视场角一样，其垂轴放大率也可能不一样。因此在像面上，畸变图像不再关于光学中心对称，而与离轴光学系统的视场角和离轴角有关，需要针对离轴光学系统的物方二维角度开展系统畸变的仿真分析。

2.1 离轴光学系统的理论畸变

对离轴光学系统理论畸变的表达式进行推导。定义(x，y)为物方坐标，(X，Y)为像方坐标。已知系统畸变的表达式为：

其中：H为像高，h为物高，β为三阶畸变系数，γ为五阶畸变系数。

将系统畸变的表达式转化为直角坐标的形式，即：

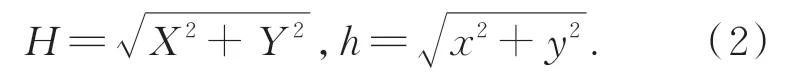
则有：

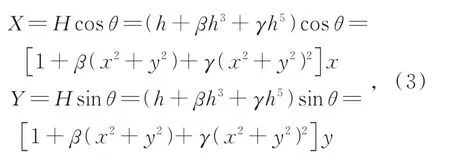
将（3）中两式展开，可得：

对公式（4）求一阶偏导数：

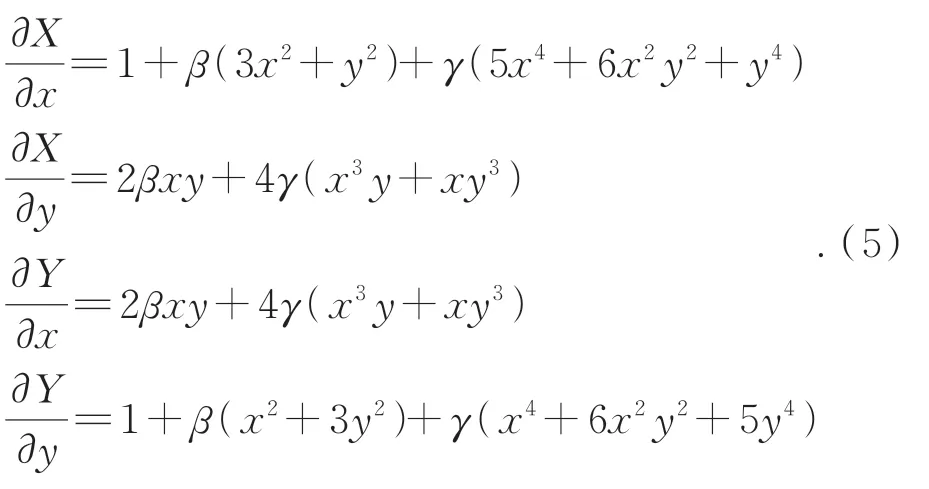
选择离轴光学系统的物方轴外某视场内的某点(x0，y0)，在其邻域内进行一阶展开，可得：

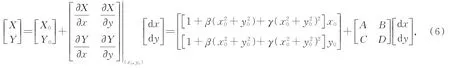
其 中：A=1+β(3x20+y02)+γ(5x40+6x20y02+y04)，B=2βx0y0+4γ(x30y0+x0y03)，C=2βx0y0+4γ(x30y0+x0y03)，D=1+β(x20+3y02)+γ(x40+6x20y02+5y04)。

式（6）中，理想像点的位置为(X0，Y0)。考虑非线性关系，在X和Y方向的放大率不同，并且有数值大小相等的交叉项存在。其中，主要部分为矩阵中的左上和右下元素，主要影响光学系统在x和y方向的放大率，次要部分是左下和右上部分，主要影响系统的偏流角度。公式可进一步表达为：

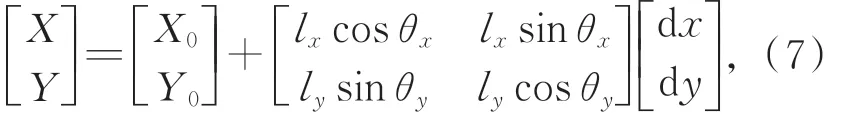
其中：

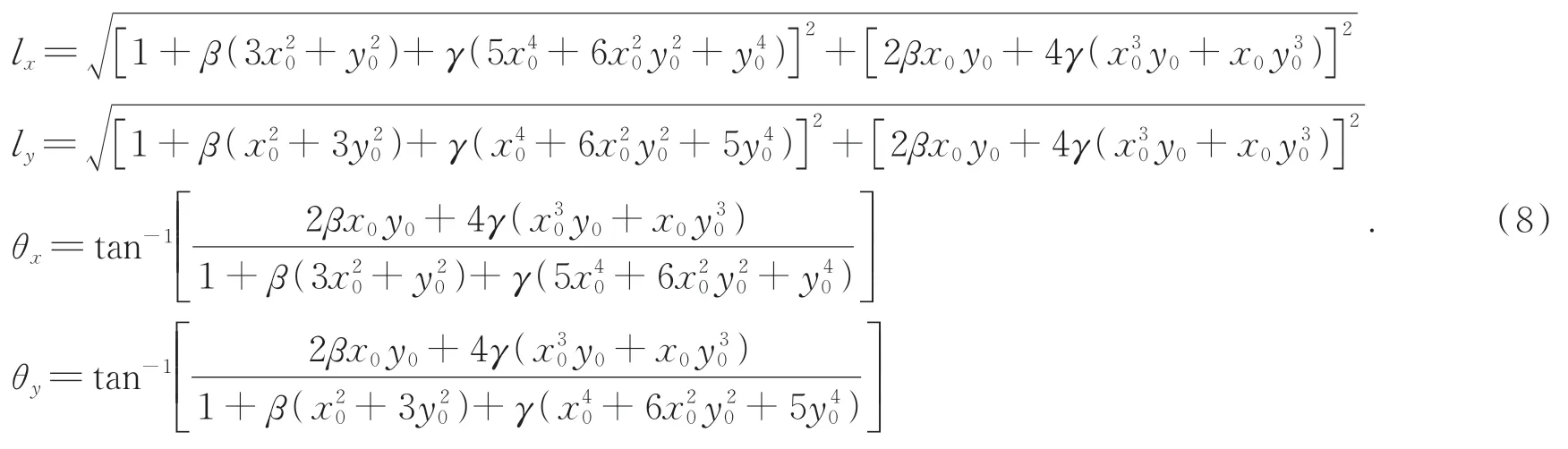
2.2 离轴光学系统的等效焦距

在上述推导的基础上，定义等效焦距为物方(x0，y0)邻域所对应的像面上的大小，则两个方向的等效焦距分别为：

其中，f为等效同轴系统焦距。

由公式（7）和（9）可知，只要解算得到离轴光学系统的高阶畸变系数β和γ，即可完成离轴光学系统的畸变分析及焦距测量。

2.3 离轴光学系统的相对畸变分离

结合ZEMAX软件中的光线追迹数据，利用多项式拟合的方法，解算得到离轴光学系统的理论高阶畸变系数。

选取某特殊视场（例如：视场角0°，离轴角4.15°），对离轴和视场方向的角度在全视场范围内进行归一化，进一步结合ZEMAX软件中的像高数据，利用Matlab中的polyfit函数对归一化后的角度量矩阵和实际像高矩阵进行五阶多项式拟合，将系统的相对畸变1.413%进行分离，最终得到光学系统的三阶畸变系数β和五阶畸变系数γ：

为了验证上述高阶畸变系数拟合的正确性和精度，将β和γ代入等效焦距公式（9），在典型的离轴角和视场角的工况下，与ZEMAX光线追迹的结果进行对比，二者的结果对比如表1所示。

表1中可以看出，当采用五阶畸变进行拟合时，最大偏差为+0.366 mm，相对偏差为+0.004 1%，拟合精度基本满足工程实际需求，接下来将利用上述系统畸变的仿真分析方法对该离轴光学系统的镜头畸变及焦距进行测量。

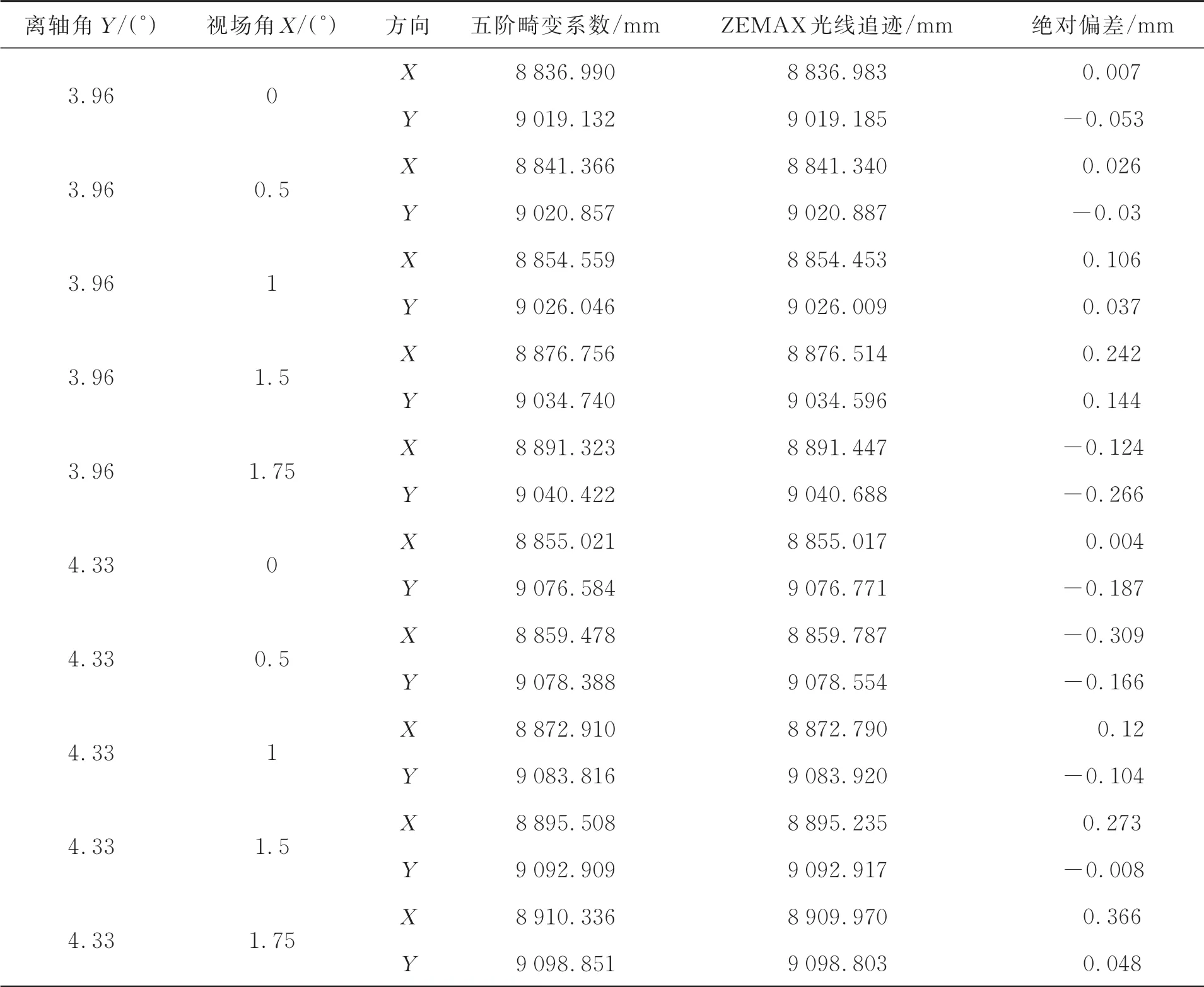
表1 五阶畸变系数计算的等效焦距与ZEMAX光线追迹结果的对比Tab.1 Comparison between equivalent focal length calculated by the fifth order distortion coefficient and ZEMAX ray tracing results

3 离轴系统的畸变及焦距测量方法

离轴光学系统的畸变测量原理如图1所示。将精细刻画和标定过的网格板精确地放置在离轴光学系统的焦平面上，并且使其刻面的中心与光轴重合。转动精密转台使其上的网格板各刻线到测位，在物方用精密测角仪在转台上绕着被测离轴光学系统的入瞳旋转观测，测量网格板上不同刻线的实际像对应的物方二维视场角。

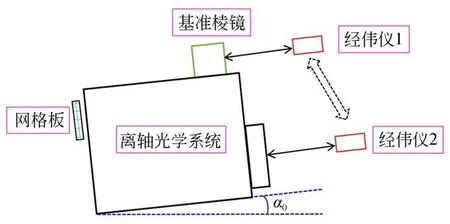
图1 畸变测量原理图Fig.1 Distortion measurement schematic diagram

具体步骤如下：

（1）经纬仪1对准离轴光学系统的基准棱镜，经纬仪2放在离轴光学系统的入光口处，利用两个经纬仪互瞄，不断调整经纬仪2的角度，使得经纬仪2瞄准离轴光学系统的中心视场，即(α0，0)，α0为系统的离轴角；

（2）将精细刻画和标定过的网格板大致放在系统的焦平面上，不断调整网格板的姿态，使得离轴光学系统入光口处的经纬仪2能够精确地瞄准网格板的中心叉丝，且经纬仪2水平、竖直扫描时能够与网格板上的特征线完全重合，此时经纬仪2已精确地放置在离轴系统的焦平面上；

（3）将经纬仪2瞄准网格板上的中心叉丝并清零二维角度，利用六维调整机构对离轴光学系统的姿态进行高精度调整，使得经纬仪分别瞄准网格板上的各刻线，以系统的中心视场(α0，0)为基准，在系统工作视场范围内，记录网格板上M×N个不同位置时经纬仪的二维角度(α0+α1，β1)，(α0+α1，β2)，…，(α0+αM，βN)。

已知离轴反射系统的离轴角为α0，进一步假设工作视场为2Δα×2Δβ，即离轴角方向的工作视场为（α0-Δα）～（α0+Δα），视场角方向的工作视场为-Δβ～Δβ，则该离轴系统工作视场内的最大空间立体角为，不论针对物方角度还是像方角度，都应采用工作视场内的最大空间立体角进行归一化，即在公式中，(x，y)为归一化后的物方角度，(X，Y)为归一化后的像方角度。物方角度归一化的计算过程为：

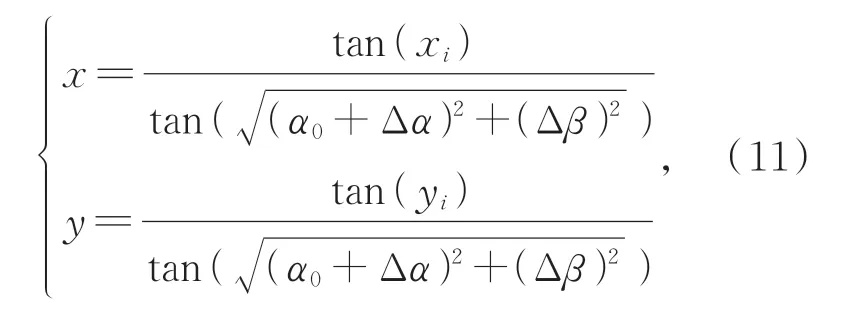
其中：物方真实角度为(xi，yi)，则归一化后的物方角度为(x，y)。

同理，像方角度归一化的计算过程见公式，像方真实角度为(Xi，Yi)，则归一化后的物方角度为(X，Y)。

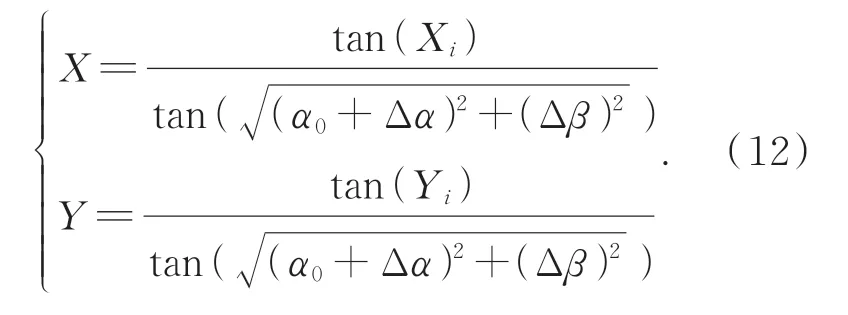
将公式进一步变形为：

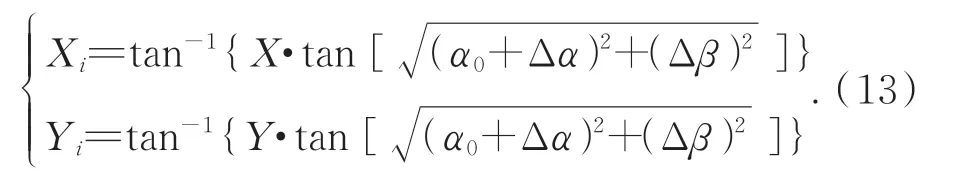
假设等效同轴系统焦距为f'，则可求得所对应的理论像高为：

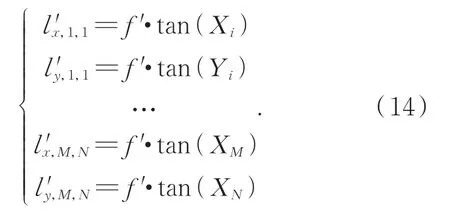
已知网格板上的各刻线对应的实际二维像高 值 为lx，1，1，ly，1，1，…，lx，M，N，ly，M，N，综 合 考 虑 离 轴光学系统M×N组理论像高和实际像高，定义评价函数为公式，当评价函数取得最小值时，即可解算得到等效同轴系统焦距为f'、三阶畸变系数β和五阶畸变系数γ：

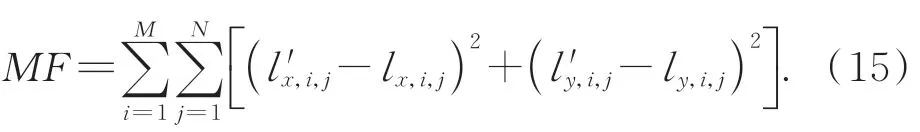
4 实验结果与分析

针对评价函数MF中，采用多维约束非线性优化方法，可以解算得到等效同轴系统焦距为f'，三阶畸变系数β和五阶畸变系数γ，物方二维角度和网格板上的像高数据见表2，解算结果见式（16），与理论等效同轴系统焦距8 750 mm相比，实测结果的偏差仅为6.378 mm，相对偏差为0.073%。

表2 物方二维角度和网格板上的实际像高数据表Tab.2 Object two dimension angle and actual image height data table on grid plate

在上述研究成果的基础上，针对在轨图像畸变校正的应用需求，还开展了探测器上特征点对应地面实际位置的应用研究。如表3所示，针对每片探测器上的3个特征点，基于上述实测的等效同轴系统焦距f'、三阶畸变系数β和五阶畸变系数γ，由像方角度可以计算得到物方角度，最终计算得到对应的地面实际位置，探测器上3个特征像元对应的地面位置如图2所示（第1片探测器的第1个特征点标为：点1-1，其余表示相同）。将该方法推广至离轴光学系统所有的探测器，即可得到离轴系统整个探测器对应的真实地物坐标，为相机在轨图像的畸变校正提供重要依据，可实现相机在轨图像准实时畸变校正。

图2 各片探测器上的特征点与地物坐标的对应关系Fig.2 Corresponding relationship between feature points on each detector and ground object coordinates

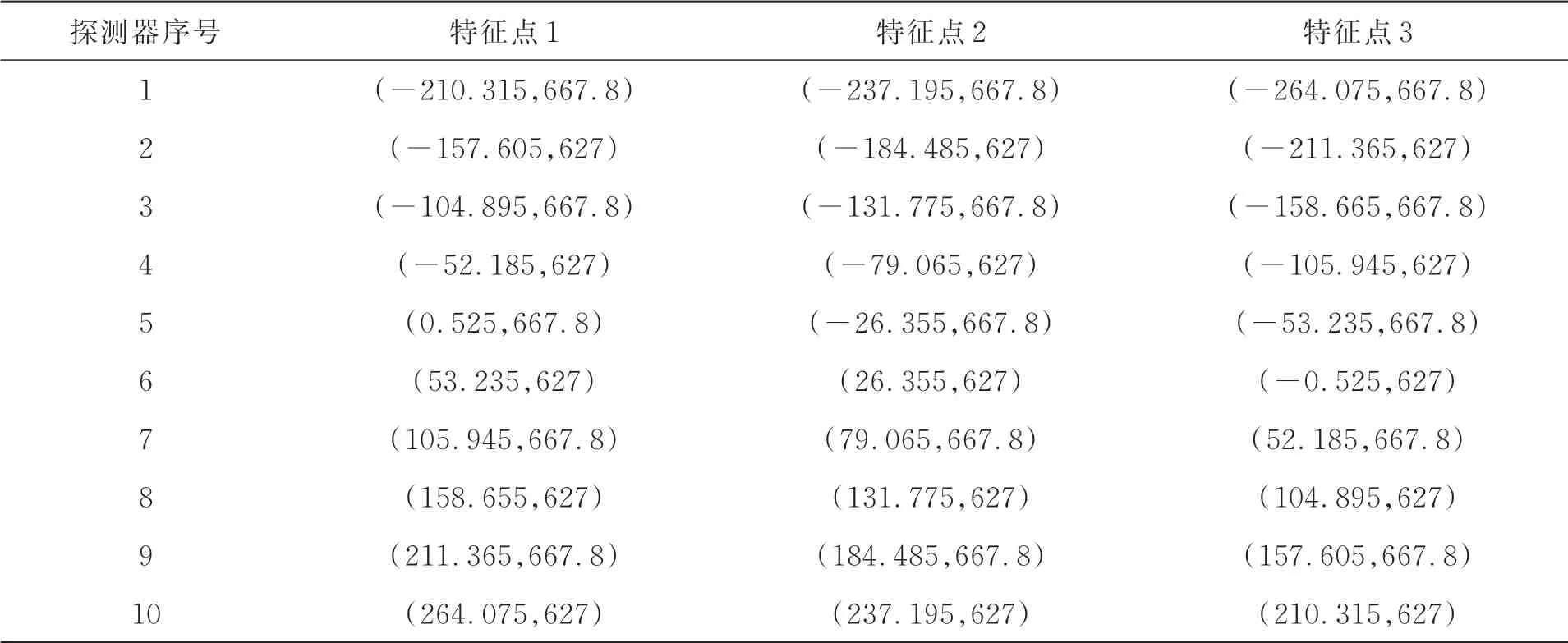
表3 每片探测器上的3个特征点坐标Tab.3 Coordinates of three feature points on each detector （mm）

5 结论

本文对离轴光学系统的理论畸变进行了分析，利用高阶畸变系数对系统的相对畸变进行了分离，并针对某装调完成的离轴光学系统，完成了畸变分析测试和焦距测量，与ZEMAX光线追迹的结果相比，等效焦距最大偏差为0.366 m，精度满足工程实际需求；针对某装调完成的离轴光学系统完成了畸变分析测试和焦距测量，实测等效同轴系统的焦距偏差仅为6.378 mm，进一步针对相机焦平面上的特征点完成了物像对应关系，为相机在轨图像的快速、高精度畸变校正提供了准确的输入。

本文初步实现了离轴光学系统的畸变分析、测试及焦距测量，下一步将综合考虑网格板的刻画精度及经纬仪的测角精度，进一步改进优化算法，提高其解算的鲁棒性，以期在未来几十米甚至一百米量级的长焦距离轴光学系统中得到更为广阔的应用前景。