高频磁致伸缩换能器输出特性测试与优化控制
黄文美,张伟帅,翁玲
(1.河北工业大学 省部共建电工装备可靠性与智能化国家重点实验室,天津 300130;2.河北工业大学 河北省电磁场与电器可靠性重点实验室,天津 300130)
1 引言
高频磁致伸缩换能器是利用磁致伸缩效应实现电-磁-机能量转换的装置,因其具有反应速度快、控制精度高、效率高等优点而被广泛应用于精密仪器、超声加工和无损检测等领域[1-2]。磁致伸缩材料易受温度和压应力等复杂工况的影响[3-4],工况的变化不仅会影响换能器的谐振频率还会对换能器最佳偏置磁场产生扰动,导致其输出性能下降[5-7]。同时,温度、负载、驱动频率和偏置磁场等影响换能器输出特性的因素之间相互作用并且存在高度非线性的关系,因此采用传统的数学方法建立换能器的输出模型具有局限性。为了提高换能器输出性能并延长换能器的使用寿命,有必要进行不同工况对换能器输出特性影响的研究并设计闭环控制系统以自动追踪换能器谐振频率和最佳偏置磁场。
目前,国内外学者关于不同工况对换能器输出特性影响的研究主要有两方面:一是对偏置磁场的影响,磁致伸缩材料存在最佳偏置磁场使其产生最大的形变量,当换能器的预应力增大时通过改变偏置磁场数值大小可提高输出位移[8-9];二是对谐振频率的影响,文献[10]利用换能器的阻抗特性研究了温度对换能器谐振频率和机电转换效率的影响,研究表明当温度升高时开环状态下的换能器谐振频率和能量转换率逐渐降低。对于自动追踪谐振频率以实现优化换能器输出性能方法主要有两种:一是锁相环闭环系统,该方法根据换能器的输入电压电流相位差可追踪谐振频率,可避免复杂的公式推导,但相位差较小时该方法极易引起追踪错误[11];二是根据换能器的谐振频率数学模型设计的自动追踪系统,该方法跟踪精度高但模型中参数较多且参数之间相互耦合,求解过程十分复杂[12]。针对换能器多根棒状材料参数存在差异从而造成阻抗分析不准确的问题,文献[13]采用分布参数法建立了换能器阻抗模型,但该模型只考虑了预应力和偏置磁场对等效模型的影响,忽略了温度对换能器输出特性的影响。文献[14]针对传统数学模型推导过程复杂且无法准确表示偏置磁场作用下换能器动态特性的问题,利用BP神经网络建立了磁致伸缩模型并研究了直流偏置磁场对磁致伸缩性能的影响,采用遗传算法和粒子群算法对神经网络的参数进行优化,但未在不同工况下对磁致伸缩材料本身性能乃至磁致伸缩器件层面性能的影响进行研究。文献[15]针对传统闭环控制系统在复杂环境下无法保证系统稳定性的问题,通过BP神经网络在线修改比例积分微分(Proportion Integration Differentiation,PID)控制器参数从而提高系统的稳定性。
本文研究了温度、负载、偏置磁场和驱动频率对高频磁致伸缩换能器输出特性的影响规律;确定了换能器工作性能优化的控制策略,随着工况的不同自动调整偏置磁场和驱动频率,建立了基于遗传算法优化的BP神经网络预测模型;设计了换能器闭环控制系统并对输出特性进行测试以验证优化控制策略的有效性。
2 磁致伸缩换能器工作原理
窗式高频磁致伸缩换能器的结构如图1所示。它由磁致伸缩材料、激磁线圈、底座、外壳和变幅杆等组成,磁致伸缩材料采用叠片结构可减小涡流损耗,两个激磁线圈采用并联的方式可减少换能器的阻抗并产生同相位磁场有利于机电能量转换。当激磁线圈中通入高频交变电流时磁致伸缩材料在交变磁场的作用下发生长度方向上的伸缩运动,将能量集中在变幅杆上以振动形式输出由此实现电-磁-机的能量转换。为避免倍频现象还需要给换能器提供直流偏置电流,使其工作在线性区间以提高换能器的输出性能。为确保换能器的振幅主要集中在变幅杆上,并提高前端和后端之间的振动速度比,变幅杆采用声阻抗较低硬质铝制成。起支撑作用的换能器外壳则使用具有较高声阻抗的不锈钢制成。
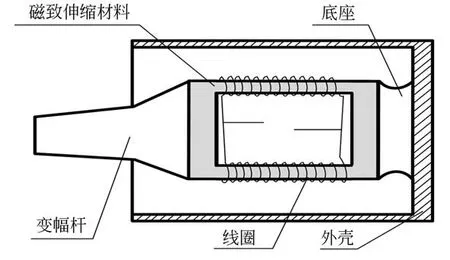
图1 窗式换能器结构模型Fig.1 Window transducer model
3 换能器输出特性测试及分析
磁致伸缩换能器的输出特性受电磁-热-机多场耦合影响。由于换能器工作在谐振频率和最佳偏置磁场时输出性能最佳,因此本文搭建了换能器阻抗特性和输出加速度测试系统并在温度20~80℃、负载0~200 N的范围内研究了不同工况对换能器谐振频率和最佳偏置磁场的影响规律。实验所用换能器的具体参数如表1所示。
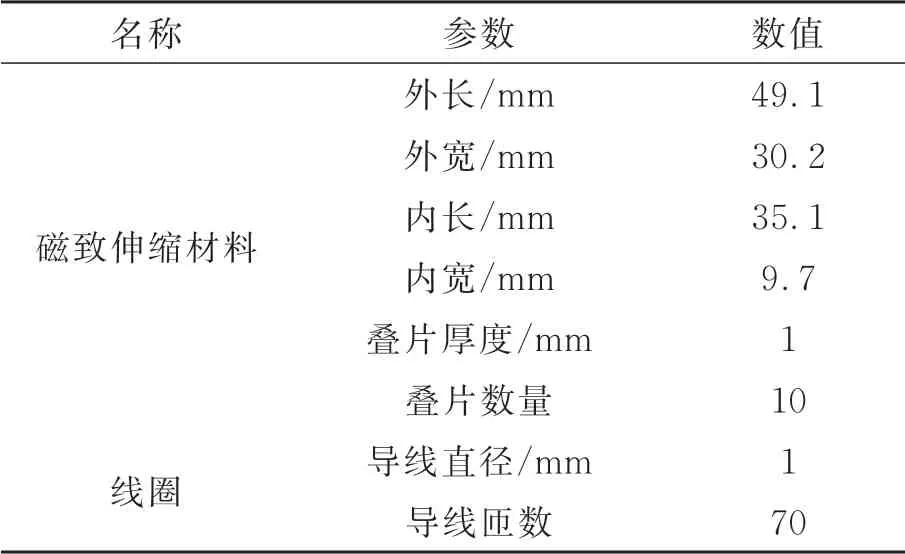
表1 换能器结构参数Tab.1 Transducer structural parameters
3.1 谐振频率漂移测试
通过阻抗圆上的谐振点可以得到换能器的谐振频率[16]。实验测试前通过自动压力机和温度控制仪设置换能器的负载F和温度T模拟不同工作环境,通过E4990A型精密阻抗分析仪对换能器的阻抗特性进行测量分析得到如图2所示的阻抗特性曲线。根据换能器阻抗特性曲线,以阻抗特性曲线中同一频率下的电阻值为横坐标,电抗值为纵坐标得到换能器的阻抗圆,由阻抗圆可知换能器的谐振频率。
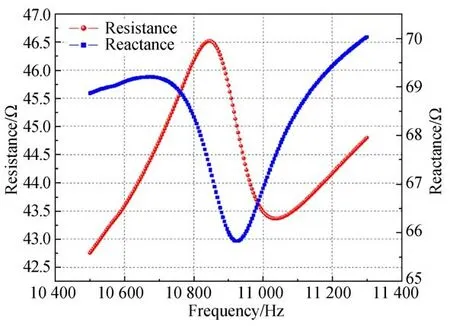
图2 换能器阻抗特性曲线Fig.2 Impedance characteristic curve of transducer
3.1.1 不同温度下阻抗圆和谐振频率的变化
当设定换能器的负载为0 N时,温度控制仪在20~80℃的温度范围内,以10℃的步长改变换能器工作温度研究温度对换能器谐振频率的影响。如图3所示为换能器工作在不同温度下的阻抗圆(彩图见期刊电子版)。
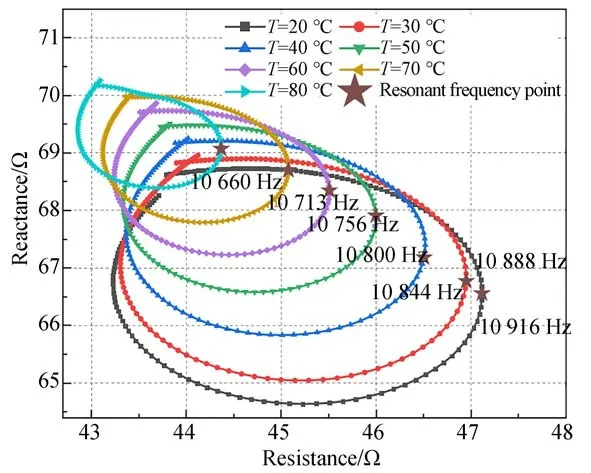
图3 不同温度下的阻抗圆(F=0 N)Fig.3 Impedance circle at different temperatures(F=0 N)
当温度升高时换能器的等效电阻呈现减小的趋势而等效电抗呈现增大的趋势,经过分析可知随着温度升高换能器的谐振频率以-4.37 Hz/℃的增长率逐渐增大,最大偏移量可达300 Hz;同时阻抗圆半径减小证明换能器的能量转换效率降低。
3.1.2 不同负载下阻抗圆和谐振频率的变化
设定换能器的工作温度为20℃时,在0~200 N的负载范围内,自动压力机以步长25 N改变换能器的工作负载以研究负载对谐振频率的影响。通过对阻抗特性曲线的分析与处理得到如图4所示换能器在不同负载下的阻抗圆(彩图见期刊电子版),结果表明:随着负载增加换能器的等效电阻、等效电抗均呈现增大的趋势,经过分析可知随着负载的增加换能器谐振频率以3.82 Hz/N的增长率逐渐增加,最大可偏移765 Hz;同时随着负载增大换能器阻抗圆半径减小证明能量转换效率降低。

图4 不同负载下的阻抗圆(T=20℃)Fig.4 Impedance circle at different loads(T=20℃)
3.2 最佳偏置磁场测试实验及扰动分析
换能器工作在谐振频率和最佳偏置磁场点时能量转换率最高,根据输出加速度变化可分析换能器最佳偏置磁场的变化情况,验证谐振频率变化规律。为了测试不同工况对换能器的最佳偏置磁场的扰动规律设计了换能器输出特性的测试系统。
3.2.1 输出特性测试系统及测试结果对比分析
换能器输出特性测试系统如图5所示,该系统主要由信号发生器、功率放大器、示波器、自动压力机、温度控制仪、磁致伸缩换能器、数据采集卡和计算机组成。信号发生器输出正弦交流信号经功率放大器放大后通过采样电阻串联磁致伸缩换能器的激磁线圈,示波器通过采样电阻的电压测量换能器驱动电流;实验测试前通过调试自动压力机和温度控制仪设置负载F和温度T模拟换能器不同的工作环境;换能器变幅杆顶端装有加速度传感器,通过DH8303型高精度数据采集卡将换能器实时加速度传输到计算机界面并进行数据处理,最终得到负载和温度对谐振频率和最佳偏置磁场的扰动规律。

图5 换能器输出特性测试系统Fig.5 Output testing system of the transducer
通过测试系统模拟换能器不同工作环境并测试换能器的输出加速度可得到换能器的谐振频率漂移情况。换能器的负载为0 N,工作温度范围为20~80℃,以10℃的步长研究温度对谐振频率的影响。不同温度下换能器输出加速度的测试结果如图6所示,结果分析得知换能器的输出加速度随着驱动频率的增加先增大后减小,可以得知换能器在某一频率下具有最大输出加速度,此时的驱动频率即换能器谐振频率;从不同温度下的曲线变化可以得知随着温度升高发生谐振频率减小的漂移现象且谐振频率处加速度呈现减小趋势。实验结果表明换能器输出装置测试谐振频率与图3的阻抗圆结果误差不超过10 Hz,可以证明该测试系统的可行性。
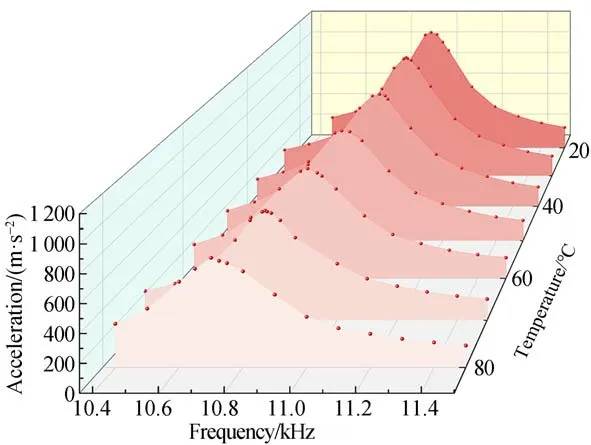
图6 不同温度下加速度与频率的关系曲线(F=0 N)Fig.6 Relationship curve between acceleration and frequency at different temperatures(F=0 N)
3.2.2 最佳偏置磁场测试实验及分析
最佳偏置磁场的确定以及不同工况下最佳偏置磁场的变化情况测试实验中,测试装置通过调整信号发生器交流信号的偏置电压改变换能器的偏置电流进而控制换能器偏置磁场。
实验中测试装置设置换能器的工作温度为20℃、负载为0 N、驱动电流幅值为0.1 A时,偏置电流IB控制在0.1~3.5 A以内,以0.1 A的步长进行最佳偏置电流的实验。当偏置电流分别为0.13 A,0.4 A,0.5 A,2.5 A,3.5 A时换能器的输出加速度的变化如图7所示,从单条曲线看,换能器加速度随着频率的增大呈现先增大后减小的趋势与温度实验结果相同;纵向分析得知随着偏置电流增大换能器谐振频率处的加速度具有先增大后减小的趋势,当偏置电流为0.5 A时加速度最大,即最佳偏置电流为0.5 A;同时随着偏置电流的增大换能器谐振频率发生100 Hz左右的漂移。偏置电流在0.1~0.5 A时,换能器的谐振频率的增长率为93.75 Hz/A;在0.5~3.5 A时,换能器的谐振频率的增长率为16.67 Hz/A。

图7 不同偏置磁场下加速度与频率关系曲线Fig.7 Relationship curve between acceleration and frequency at different bias magnetic fields
3.2.3 温度对最佳偏置磁场的扰动影响
当工作负载为0 N时,测试装置在20~80℃的范围内调整温度控制仪以步长为10℃控制换能器的温度、在0.1~2 A的范围以0.1 A的步长控制换能器的偏置电流,测量在不同的温度下换能器加速度随偏置电流的变化情况。图8所示为不同工作温度下换能器的加速度(彩图见期刊电子版),从单条曲线看,随着偏置电流增大换能器加速度先增加后减小,在最佳偏置电流处加速度幅值最大;纵向分析得换能器的输出加速度随温度升高呈现减小的趋势,同时温度的升高使换能器的最佳偏置电流以近似11.67 mA/℃的增长率逐渐增大。

图8 不同温度时加速度与偏置电流关系曲线(F=0 N)Fig.8 Relationship curve between acceleration and bias current at different temperatures(F=0 N)
3.2.4 负载对最佳偏置磁场的扰动影响
当换能器工作温度为20℃时,测试装置通过调整自动压力机在0~200 N的范围以25 N的步长控制换能器负载、在0.1~2.5 A的范围内以0.1 A的步长控制换能器的偏置电流,测量在不同负载下换能器输出加速度随偏置电流的变化情况。换能器在不同负载下的输出加速度如图9所示(彩图见期刊电子版),分析可知:负载固定时,换能器的加速度随着偏置电流增大先增大后减小;纵向看,随着负载的增大换能器同一偏置电流下的加速度呈现减小的趋势,同时换能器的最佳偏置电流以近似6.67 mA/N的增长率逐渐增大。

图9 不同负载时加速度与偏置电流关系曲线(T=20℃)Fig.9 Relationship curve between acceleration and bias current under different loads(T=20℃)
4 BP神经网络预测模型
BP神经网络只需数据样本而无需建立数学模型就可以建立任意连续函数输入与输出之间的非线性映射关系[17]。本文基于第3节的实验测试数据,采用单隐含层的神经网络来表征温度和负载与谐振频率和最佳偏置电流之间的非线性关系,建立不同工况下换能器谐振频率和最佳偏置电流的预测模型。
4.1 BP神经网络模型
根据测试装置对不同工况下换能器的谐振频率以及最佳偏置电流的漂移测试得知,谐振频率fs是关于温度T、负载F以及最佳偏置电流IDC的三元函数,而最佳偏置电流是关于温度和负载的二元函数,将式(2)代入式(1)中得到式(3),即谐振频率为关于温度和负载的二元函数。
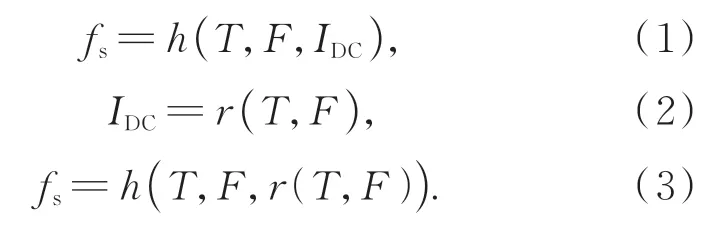
根据上述实验分析以及公式推导将换能器测试的温度T和负载F作为神经网络的输入参数,换能器的谐振频率fs和最佳偏置电流IDC作为神经网络的输出参数。BP神经网络的结构如图10所示。

图10 BP神经网络模型Fig.10 BP neural network model
神经网络结构中,隐含层节点个数为:
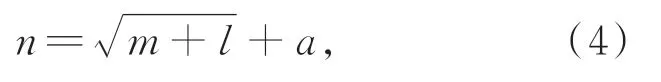
式中:m为输入层节点个数,l为输出层节点个数,a为1~10之间的整数,此实验中,输入节点m为2,输出节点l为2。其中i1,i2是BP神经网络的输入值,ωij和ωjk(i=1,2;j=1,2,…,n;k=1,2)分别表示输入层与隐含层单元节点之间的权重值和隐含层与输出层单元节点之间的权重值,j1~jn表示隐含层内神经单元节点,k表示输出层的神经单元节点。输入层的输入与输出表示为:

隐含层的输入与输出分别为:

输出层的输入与输出分别为:
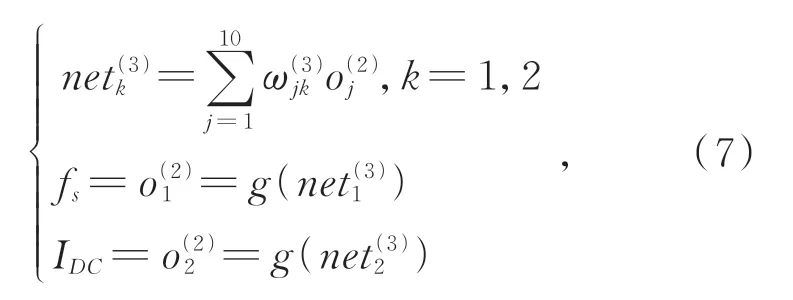
式中:f()为隐含层神经元活化函数,g()为输出层神经元活化函数。
4.2 BP神经网络预测模型的学习与优化
为准备神经网络的训练数据,将第2节测量的数据:负载一定时温度分别为20℃,30℃,…,70℃,80℃的7类数据样本以及温度一定时负载分别为0,25 N,…,175 N,200 N的9类数据样本,共可得到63组不同温度和负载下谐振频率和最佳偏置电流的数据样本。63组(T,F,fs,IDC)四维数组中的45组实验数据作为训练样本,剩余18组实验数据作为神经网络的测试数据。通过输入参数和输出参数的个数确定BP神经网络拓扑结构,从而确定神经网络的权值和阈值的个数;通过遗传算法和粒子群算法对BP神经网络的权值和阈值进行求解与优化,实现不同工况下对换能器谐振频率和最佳偏置电流的精准预测。以遗传算法优化BP神经网络(GA-BP)为例,具体算法流程如图11所示。该GA-BP神经网络的隐含层和输出层活化函数均为purelin函数,训练方法采用梯度下降法,隐含层节点个数为11,最大训练步数为1 000次,训练误差为0.000 01,学习速率为0.01,初始化的种群规模为10,最大进化代数为50,交叉概率为0.9,变异概率为0.1。

图11 GA-BP神经网络算法流程图Fig.11 Flow chart of GA-BP neural networks algorithm
在相同的训练样本和测试样本下,分别采用传统BP神经网络、粒子群优化的BP神经网络(PSO-BP)以及遗传算法优化的BP神经网络(GA-BP)三种模型对换能器的谐振频率和最佳偏置磁场电流进行预测,预测结果如图12所示。

图12 不同模型的预测结果与误差Fig.12 Prediction results and errors of different models
根据预测结果可以看出传统的BP神经网络的预测结果误差较大,这是因为BP神经网络的最优权值和阈值无法准确获得,相比之下经过遗传算法和粒子群算法对权值和阈值优化后的GA-BP神经网络和PSO-BP神经网络的误差较小。各预测模型的误差具体数值见表2。
根据表2数据可知GA-BP神经网络与PSOBP神经网络的预测误差相近但前者的学习速度快,所以本文选择GA-BP神经网络预测模型。随着工况的变化GA-BP神经网络对谐振频率预测的平均误差为20.5 Hz,最大误差为60.06 Hz;对最佳偏置电流预测的平均误差为31.4 mA,最大误差为68.68 mA,此误差与复杂环境引起的扰动相比较小,可以忽略不计。利用神经网络追踪最佳偏置磁场和谐振频率的方法与其他方法的预测对比如表3所示,根据表3可知神经网络预测模型比函数模型的拟合度更好、误差更小同时避免了锁相环不能追踪最佳偏置磁场的缺点[11]。

表2 不同预测模型的预测误差Tab.2 Prediction error of different prediction models

表3 不同追踪方法的预测对比Tab.3 Prediction comparison of different tracking methods
利用GA-BP神经网络建立换能器谐振频率和最佳偏置电流的预测模型,解决了换能器由于各参数之间相互耦合嵌套难以建立理论模型的问题,为优化和预估换能器输出性能提供了新的方法。
5 基于GA-BP神经网络预测模型的闭环控制系统
为优化换能器输出性能,本文基于GA-BP神经网络预测模型设计了不同工况下可自动追踪换能器谐振频率和最佳偏置电流的闭环控制系统,并对该闭环控制系统和换能器的输出性能进行了测试。
5.1 闭环控制系统的设计
换能器闭环控制系统如图13所示,交流驱动部分通过整流电路、Buck电路和逆变电路实现谐振频率的追踪,直流偏置部分通过整流电路和LLC谐振电路追踪最佳偏置电流,耦合电路叠加交流驱动电流和直流偏置电流为换能器提供励磁电流。当换能器工况变化时,由传感器将此时工作温度T和负载F输入DSP控制系统,DSP控制系统通过PWM1,PWM2和PWM3控制交流驱动信号的幅值、频率以及直流偏置电流实现谐振频率和最佳偏置电流的自动追踪,达到优化换能器输出性能的目的。

图13 高频磁致伸缩换能器闭环控制系统Fig.13 Closed-loop control system for high frequency magnetostrictive transducer
闭环控制系统的DSP控制系统如图14所示,以温度T和负载F为输入量、偏置电流IB和驱动频率f为控制量。温度传感器与力传感器感知换能器温度和负载经ADC转换输入DSP控制芯片中,GA-BP神经网络预测模型对换能器的谐振频率fs和最佳偏置电流IDC预测后通过调整PID控制器参考值从而实现谐振频率和最佳偏置电流的自动追踪。

图14 基于GA-BP神经网络的DSP控制系统Fig.14 DSP control system based on GA-BP neural network
耦合电路利用电感的“通直隔交”特性和电容的“通交隔直”特性将直流偏置和交流驱动电流叠加得到换能器的总激磁电流,实现电-磁-机的能量转换。单激磁线圈的交直流耦合电路设计可消除双激磁线圈设计中交流线圈和直流线圈的互感影响,同时解决了直接增加偏置电压时交直流信号中的直流信号无法通过匹配电容而失去偏置磁场等问题。
5.2 闭环控制系统测试实验
为了验证采用基于GA-BP神经网络预测模型的闭环控制系统来优化换能器输出性能的可行性,本文对不同工况下的磁致伸缩换能器输出加速度进行了测试。通过自动压力机和温度控制仪模拟不同的工作环境,利用压电式加速度传感器测量磁致伸缩换能器在闭环控制系统控制前后的输出加速度,同时对换能器的驱动频率和偏置电流进行测量。
图15所示为换能器负载F由0 N突变为100 N时偏置电流的变化过程,此时换能器的最佳偏置磁场电流由原来的0.5 A变化为1 A。从图中可以看出,在负载发生突变后,经典PID控制系统经过调整后偏置电流仍恢复为原初始值0.5 A,而基于GA-BP神经网络的闭环控制系统可以自动追踪并快速稳定在新的最佳偏置电流值1 A。此外,基于GA-BP神经网络的控制系统响应更快,超调量更小,展现了良好的鲁棒性和稳定性。
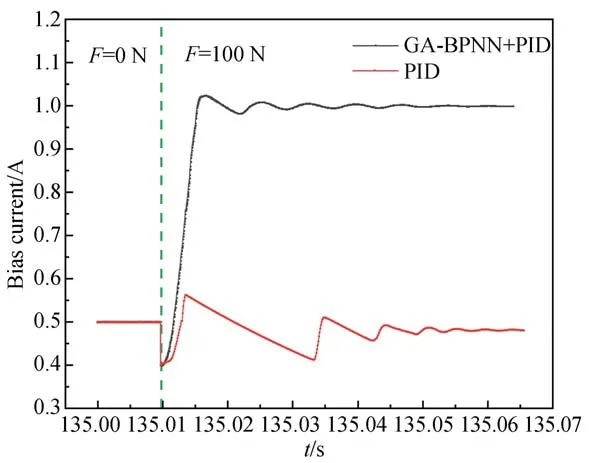
图15 换能器负载突变时偏置电流的变化过程Fig.15 Process of bias current change when transducer load is abrupt
不同工况下换能器经过闭环控制系统控制后的驱动频率、偏置电流以及输出加速度峰值在控制前和控制后的对比如图16所示,图16(a)和图16(b)为负载为0 N、工作温度为20~80℃时换能器在闭环控制系统控制前后输出加速度对比、驱动频率和偏置电流,从图中可以看出换能器的驱动频率从10.916 kHz减小到10.66 kHz、驱动电流从0.5 A增大到1.2 A,而加速度的峰值在控制后比控制前增加了0~56.8%,平均增加了28.4%;图16(c)和图16(d)为工作温度为20℃、负载为0~175 N时换能器在控制前后的输入输出数据对比,换能器的驱动频率从10.916 kHz增加为11.6 kHz、偏置电流从0.5 A增大为1.67 A,换能器的加速度峰值在闭环控制后比控制前增加了0~45.8%,平均可增加22.9%。对比换能器经闭环控制系统控制前后的输出加速度发现该控制系统可使换能器输出加速度幅值平均提高25.65%,证明了该控制系统优化输出性能的有效性。
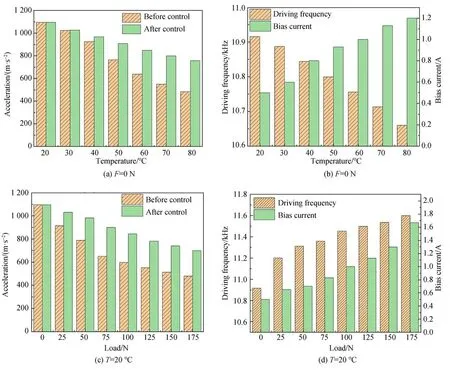
图16 闭环控制系统控制前后的换能器加速度峰值对比Fig.16 Comparison of peak acceleration of the transducer before and after the closed-loop control system
工况变化所导致的换能器最佳工作点变化会使其偏离线性工作区。这不仅导致换能器输出加速度峰值减小还会使其加速度波形产生畸变。表4为控制后的换能器驱动频率、偏置电流和换能器输出加速度峰值的具体数值,图17所示为4种工况下换能器在基于GA-BP神经网络的闭环控制系统控制前后的输出加速度波形对比。

表4 不同工况下闭环控制前后的数据Tab.4 Data before and after closed-loop control under different working conditions

图17 闭环控制系统控制前后的换能器加速度波形对比Fig.17 Comparison of transducer acceleration waveform before and after control by closed-loop control system
从图17中可以看出闭环控制系统控制后的换能器输出加速度峰值和波形均得到优化,尤其图17(b)和图17(d)由于谐振频率和最佳偏置磁场变化较大,导致控制前的加速度波形发生明显畸变。通过对比闭环控制系统控制前后的换能器输出加速度的峰值和波形表明:基于GA-BP神经网络的闭环控制系统在换能器工况发生变化时可以不依赖数学模型而准确预测并追踪换能器的谐振频率和最佳偏置磁场,实现优化输出性能的目的。
6 结论
针对复杂工况下磁致伸缩换能器的谐振频率和最佳偏置磁场的漂移导致其输出性能变差的问题,本文设计了温度可调、负载可变的换能器输出特性测试系统,测试了温度和负载的变化对换能器的谐振频率以及最佳偏置磁场的影响,构建了闭环控制系统优化换能器的输出性能,主要结论如下:
(1)在温度T为20~80℃、负载F为0~200 N的范围内时,随着负载的增加,换能器的谐振频率和最佳偏置磁场均呈现逐渐增加的趋势;随着温度的升高,换能器的谐振频率逐渐减小,而最佳偏置磁场逐渐增加。
(2)为表征温度T和负载F与谐振频率fs和最佳偏置磁场电流IDC之间的非线性关系,本文以负载和温度为输入参数,以谐振频率和最佳偏置磁场电流为输出参数,基于遗传算法优化的BP神经网络建立不同工况下换能器的谐振频率和最佳偏置电流的预测模型。
(3)搭建闭环控制系统,利用GA-BP神经网络预测模型与PID控制系统相结合实现换能器的谐振频率与最佳偏置磁场电流的实时自动追踪。实验结果表明:当换能器工况发生变化时,该闭环控制系统可有效地提高换能器的加速度峰值25.65%同时优化加速度波形。
本研究可为大功率磁致伸缩超声换能器的高效工作和广泛应用提供理论和技术支持。

