基于并联卷积神经网络的水果品种识别
李 超,李 锋,黄炜嘉
(江苏科技大学 电子信息学院,江苏 镇江 212000)
随着人工智能技术的发展,基于图像的物品识别技术得到广泛应用。在农产品分类方面,传统的图像识别算法主要用于数据集的预处理和特征提取方面[1-3],其准确度依赖于人工提取特征[4-6]的结果,难以处理当前大数据量的高分辨率图片。深度学习技术的发展,为解决这一问题提供了新的路径。目前,深度卷积网络在植物领域[7]已得到广泛应用,研究人员先后提出了VGG、GoogLeNet、ResNet等网络模型[8-10],并有学者将其用于农产品图像分类识别领域[11-14]。但是,这些模型较为简单,训练周期长,且准确率偏低。针对这一问题,本文首先利用BEGAN[15]网络对Fruit-360数据集进行数据增强,然后在Tensorflow平台上进行预处理,将数据集转换成128×128×3大小的TfRecord文件进行批次处理,利用改进的并联卷积神经网络提取更多的特征信息,利用ELU[16]激活函数代替ReLU激活函数,利用最大类间距损失函数代替传统的SoftmaxWithLoss损失函数来提高相似类间的识别准确率,最后通过实验与传统的识别算法进行比较。结果显示,本文提出的算法有效地提高了网络的识别准确率。研究结果可以为相关研究提供借鉴与参考。
1 卷积神经网络(CNN)
1.1 卷积神经网络的基本结构
典型的卷积神经网络,其网络结构由卷积层、池化层、全连接层、输出层构成[17-18](图1)。其中,卷积层是核心部分,其过滤器通过权值共享策略来提取信号特征;池化层通过最大池化或者平均池化的方法来减少训练参数,加快训练速度;全连接层将得到的特征信息组合在一起;输出层进行分类预测。

图1 卷积神经网络模型示意图Fig.1 Schematic diagram of convolution neural network model
卷积神经网络通过前向传播来提取图像特征,是一个线性模型,其前一层的输出是后一层的输入,但这样容易出现线性能力表达不够的问题。为了去线性化,需要引入一个非线性的函数,即激活函数。最后,将激活函数加入到神经网络中。上述过程涉及的主要数学模型如下:
(1)
μt=W(t)x(t-1)+b(t);
(2)
x(t)=f[μ(t)]。
(3)
式(1)~(3)中:μ、W、b、t、x、f分别表示输出、权值矩阵、偏置项、卷积神经网络的数、输入、激活函数。
在训练前馈神经网络的过程中,通过反向传播的算法来更新参数,利用期望输出与实际输出之间的差异来得到代价函数。然后,通过代价函数反向传播,即通过梯度下降算法来调整W和b。
1.2 模型构架
传统的卷积神经网络只能在上一层的基础上提取到固定尺度的特征。为实现多尺度的特征提取,本文设计了一个有着不同尺度卷积核的并联卷积神经网络,以此来实现不同尺度特征的同步提取,以使特征表达更加丰富,让网络可以提取到更多的特征信息。对网络模型(图2)简述如下。输入的图像为预处理后的图像,通过卷积池化等操作进行特征提取,C1、C2为16个3×3的卷积核,使用全0填充,步长为1,输出为128×128×3。S1为2×2的最大池化层,步长为2,输出为64×64×16。C3为16个大小为3×3的卷积核,使用全0填充,步长为1,输出为64×64×16。C4为16个大小为3×3的卷积核,使用全0填充,步长为1,输出为64×64×16。S2为大小为2×2的最大池化层,步长为2,输出为32×32×16。将生成的特征图像输入到a、b两个并联通道中:a通道包含32个3×3的卷积层和1个2×2的最大池化层,卷积层使用全0填充,步长为1,池化层步长为4;b通道包含32个5×5的卷积核和2个2×2的最大池化层,卷积层使用全0填充,步长为1,最大池化层的步长为2。a、b通道各生成32个8×8的特征图,将2个通道所生成的64个8×8的特征图作为C5的输入。C5和C6为64个大小为3×3的卷积层,使用全0填充,步长为1。S3为大小为2×2的最大池化层,步长为2。最后为全连接层,将卷积层和池化层具有分类信息的局部信息进行整合,然后输出。

图2 改进的网络模型结构示意图Fig.2 Schematic diagram of improved network model
1.3 激活函数
激活函数在实现网络模型非线性化的过程中具有重要作用。常用的激活函数,如Sigmoid和Tanh激活函数,会随着样本越多出现梯度消失问题;ReLU激活函数会出现某些神经元永远不被激活,相应的参数得不到更新的问题。针对ReLU激活函数存在不稳定性的问题,本文采用ELU[17]激活函数代替ReLU激活函数。ELU激活函数具有左软饱和的特性,能够减小梯度消失的影响。
1.4 损失函数
在识别多分类问题时,常使用SoftmaxWithLoss或者Triplet loss作为损失函数。但是,SoftmaxWithLoss不对不同品种的特征进行限制,对同一类别不同品种的识别准确率不高,相似的图片会被分到同一品种中,因此泛化能力和稳健性不强;而Triplet loss过于关注同一品种内部的关系,导致样本分散。针对以上问题,本文引用最大类间距损失函数来增大相似品种间的距离,以提高对相似品种的识别准确率。最大类间距损失函数的公式如下:
(4)
(5)
式(4)、(5)中:L表示最大类间距损失函数;i代表第i类水果;j代表第j类水果;m代表总的水果种类数;M(i)表示第i类水果的均值;M(j)代表第j类水果的均值;n代表第e个品种的样本数量;x(i,e)代表第i类水果第e个品种的值;hw,b[x(i,e)]=wx(i,e-1)+b,w表示第e个品种的权值。
将最大类间距损失函数与SoftmaxWithLoss损失函数结合,得到
J=S-λL。
(6)
式(6)中:J表示本文引入的新的损失函数,S表示SoftmaxWithLoss损失函数,λ表示超参数。
通过在新的损失函数中引入最大类间距损失函数,相似品种间的间隔会越来越大,随着训练步数的增多,J的值会越来越小,相似品种间的分类也就变得越来越准确。
对J求导,可得
(7)
式(7)中:f、l、N分别表示激活函数、卷积层数、样本数量。
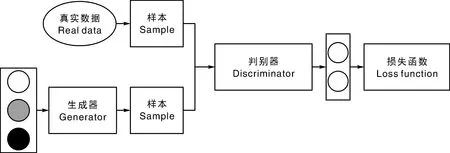
图3 边界均衡生成对抗网络的结构示意图Fig.3 Schematic diagram of boundary equilibrium generative adversarial network
2 基于边界均衡生成对抗网络(BEGAN)的数据增强
传统的数据增强方法不改变图像标签,只对已有样本进行旋转、平移、翻转、缩放等几何变换,这些变换在一定程度上可以缓解过拟合问题,但无法从根本上解决数据集不足的问题,而且,其中多需要凭借经验进行函数和参数的设置,很难实现最优的数据增强。本文在传统数据增强的基础上,引入BEGAN[18]。该网络由判别器和生成器组成,利用博弈的方式对模型进行训练:判别器通过生成器传递的参数来调节自己的参数,以此来判断传入数据的真伪;生成器主要通过判别器传递的损失函数来更新自己的参数,以此来生成更多难以被判别器判断的数据。最终,两个模型达到一个平衡点,训练结束。其优点是,生成的数据集并不来自数据样本,而是通过判别器传过来的参数生成全新的数据集。相比传统的数据增强,基于BEGAN生成的数据集质量更高。其网络结构如图3所示。此网络能够控制图像的多样性,生成更高质量的数据集。
网络模型框架分别如图4和图5所示,其中:
判别器部分由4个卷积模块和1个全连接层组成,除了第一个卷积模块采用的是3个3×3的卷积层外,其他3个模块均由1个1×1和2个3×3的卷积层外加1个池化层堆叠而成;生成器的网络结构采用5个卷积模块,每个模块均由2个3×3的卷积层和1个上采样层构成。判别器与生成器的衔接处由2个全连接层构成。

图4 判别网络结构Fig.4 Discriminating network structure

图5 生成网络结构Fig.5 Generate network structure
判别器(D)、生成器(G)在第t步的损失函数为
(8)
式(13)中:LD、LG分别表示D、G的损失函数;kt表示在对LD进行梯度下降的时候,L[G(zD)]的梯度大小;λk是学习率k的比例增益,在本研究中令λk=0.001;γ是为在训练中保持生成器与判别器损失之间平衡而引入的系数。当γ取值较小时,生成的图片较为清晰,但是较为单一;当γ取值增大时,生成的图片多样性增大,但是图片较为模糊,不利于细粒度图像分类。为了生成精细度高的数据集,本文使用较小的γ值,取值0.001。zD、zG均采样自均匀随机样本z。
3 结果与分析
3.1 数据集制备
3.1.1 数据集选取
本实验选用公共数据集Fruit-360。该数据集包含81种水果55 244张图像,分辨率为100×100×3。本实验从中选取8种水果[分别为Apple Braeburn(布瑞本苹果)、Apple Crimson Snow(红雪苹果)、Apple Golden2(金色苹果2)、Apple Golden3(金色苹果3)、Cherry1(樱桃1)、Cherry2(樱桃2)、Cherry Rainier(Rainier樱桃)、Cherry Wax Black(蜡黑樱桃)]的图像作为训练集和测试集,用来检验本文提出的卷积神经网络的准确率,并与其他方法进行对比。上述8个品种的部分图像如图6所示。

图6 实验用水果品种的图像示意Fig.6 Images of fruit varieties used in experiment
3.1.2 数据增强
实验之前,将图片大小转换成128×128×3,使用NVIDIA GTX1080Ti GPU进行加速。以Cherry Rainier品种为例,为了生成较为精确的图片,选取γ=0.001,迭代10 000次,设置学习率为0.000 07,输入350张128 pixel×128 pixel的RGB图片,开始训练。
迭代5 000次时,樱桃的特征清晰可见,但生成的图片对比度不高;迭代10 000次时,图片有了更多的细节信息,对比度和亮度提高,颜色更为逼真(图7)。
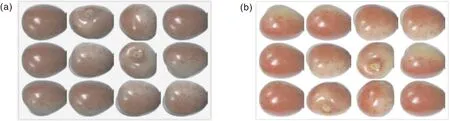
图7 迭代5 000次(a)和10 000次(b)后的结果Fig.7 Result after 5 000 (a) and 10 000 (b) iterations
通过生成一系列高质量的数据集,可以有效地避免过拟合现象。
为了验证基于BEGAN的数据增强算法的质量,选择使用传统数据增强(平移、旋转)算法的数据集和仅使用BEGAN算法的数据集在Lenet-5网络模型上进行训练,训练步数均为5 000次,学习率为0.001,动量设置为0.8,每个品种的样本数量为1 300,通过自动更改学习率的方式进行训练,得到各数据集的准确率(表1)。使用传统方法进行数据增强的,其平均识别率为93.51%;使用BEGAN进行数据增强的,其平均识别率为95.66%,效果更优。
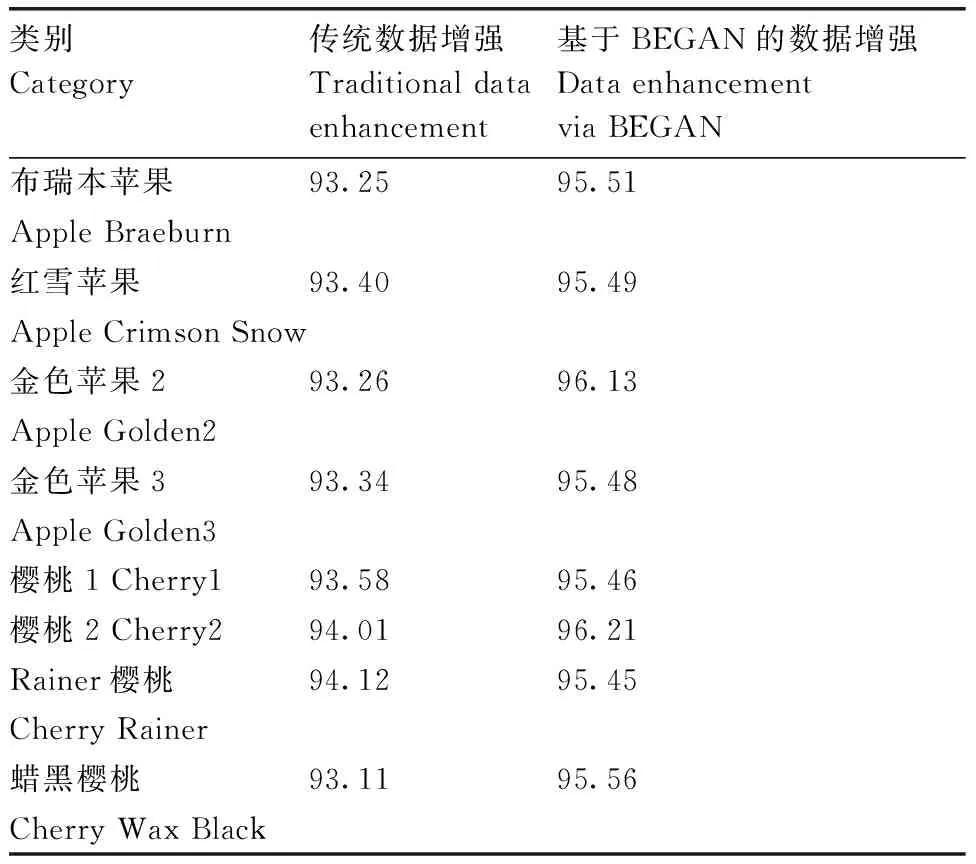
表1 BEGAN算法与其他数据增强算法的准确率对比
为了获得更多数量的数据集,本实验先使用BEGAN生成高质量的数据集,然后再结合传统的数据增强方法来扩大数据集。为了确定样本数量数对准确率的影响,以同样的方法对不同样本数量的数据集进行训练。随着数据集中样本数量的增加,其在8种水果上的平均识别准确率也随之增加(图8):当样本数量在500~2 000时,识别准确率上升较快;当样本数量在2 000~3 000时,准确率提升缓慢;当样本数量在3 000~3 200时,准确率趋于平稳,识别准确率为96.5%。综合考虑训练效率与准确率,选择每个品种的样本量为3 200左右。

图8 不同样本数量对准确率的影响Fig.8 Effect of different sample quantity on accuracy
3.2 不同模型的结果对比
采用数据增强后的水果数据集进行实验,其中,80%用作训练集,20%用作测试集。为了提升参数更新的速度、获得参数值的最优解,采用小批量梯度下降法。设定每次传入模型的数据集样本数量为64,权重衰减次数为0.01,学习速率为0.005。与传统的目标识别算法相比,卷积神经网络省去了对图片的预处理、特征提取、品种分类等过程,只需要将图片的分辨率统一设置为128 pixel×128 pixel,然后输入到训练模型中,就可以同时实现上述过程,提高了训练效率。使用并联卷积神经网络和去掉a通道后的串联卷积神经网络在训练集上进行实验。可以看出,两者的准确率在前170步均上升较快,在170步以后趋于平稳,其中,采用串联卷积神经网络的准确率在96.74%左右,采用并联卷积神经网络的准确率在97.81%左右(图9)。两者的损失值在前180步下降明显,之后趋于平稳,采用串联卷积神经网络的损失率在3.5%左右,采用并联卷积神经网络的在2%左右(图10)。综上,采用并联卷积神经网络的,其效果要优于采用串联卷积神经网络的。

图9 不同网络模型的准确率对比Fig.9 Comparison of accuracy of different network models
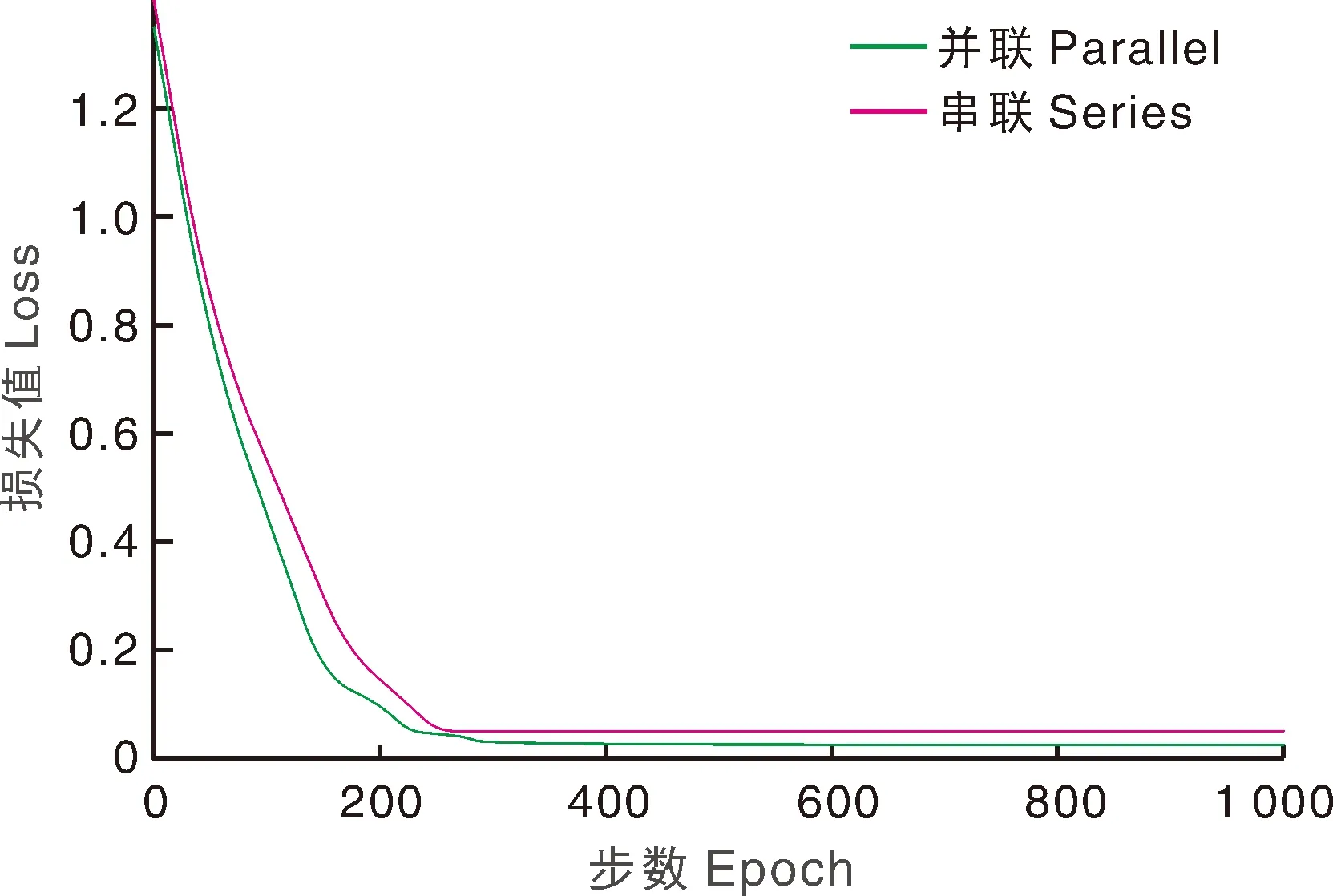
图10 不同网络模型的损失值对比Fig.10 Comparison of loss of different network models
对比使用不同损失函数(将引入最大类间距损失函数并与SoftmaxWithLoss结合的,称为新损失函数;将使用SoftmaxWithLoss损失函数的,称为旧损失函数)在并联卷积神经网络训练集上的准确率和损失值。无论使用哪种损失函数,其准确率在前200步均上升明显,之后趋于平稳,其中,采用新损失函数的准确率可以达到99%(图11)。两种损失函数下,损失值均在前300步下降明显,之后趋于平稳,其中,采用新损失函数的损失值趋近于0(图12)。这说明,本研究设计的网络模型和引入的新损失函数能够完成对多种水果品种的识别。

图11 不同损失函数的准确率对比Fig.11 Comparison of accuracy of models with different loss functions
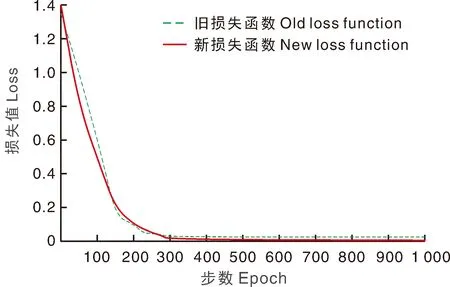
图12 不同损失函数的损失值对比Fig.12 Comparison of loss of models with different loss functions
统计使用不同损失函数时,每个品种的识别准确率(表2)。使用旧损失函数时,8种水果的平均识别率为97.87%;使用新损失函数时,8种水果的平均识别率为98.85%。这说明,新损失函数在识别相似品种时,具有更高的识别准确率。

表2 引入不同损失函数的识别准确率
进一步对比不同模型的识别准确率,具体包括本文提出的模型(以下简称本文模型)、去掉本文模型中左半支a通道的单只卷积神经网络结构(以下简称为舍去a通道的单只CNN),以及其他学者提出的特征加强+BP神经网络[5]、形状相似的水果自动识别[11]、特征提取+单只CNN[13]。其中,本文模型的准确率达到98.85%,识别率最高(表3)。这说明,采用并联卷积神经网络将不同大小的卷积核并联,实现多尺度的特征提取,同时引入稳健性更强的激活函数,采用最大类间距损失函数与SoftmaxWithLoss相结合的新损失函数,有助于提升对相似品种的识别准确率,而且,该方法解决了传统算法中人工提取特征的缺陷。

表3 不同模型的准确率对比
4 结论
针对水果品种识别,本文设计了一种并联卷积神经网络,对多尺度特征进行同步提取,采用ELU激活函数代替传统的ReLU激活函数来减小梯度消失的影响。针对数据集过少的问题,采用BEGAN结合传统数据增强方法生成大量高质量的数据集,减少过拟合现象。针对相似水果品种识别率不高的问题,引入最大类间距损失函数并与SoftmaxWithLoss损失函数联合,来增大相似类间的距离,提高对相似品种的识别准确率。本文模型与传统的神经网络相比,具有更高的识别率,是一种有效的目标识别算法。

