基于新型速度规划的优化算法研究*

苟凌铭，唐樟春,2※，李征泰，高 伟

（1.电子科技大学机械与电气工程学院，成都 611731；2.电子科技大学广东电子信息工程研究院，广东东莞 523808）

0 引言

运动控制的要求要减小运动控制系统在启动、停止、加速和减速运动阶段的振动与冲击[1]，因此运动控制规划中加减速的规划设计与插补是运动控制系统性能的保证。本文基于一种优化后的新型加减速规划算法为计算理论，以时间分割思想为基础，采用以路径误差为核心，细分路径过程的方式来进行插补运算，从而实现规划约束中速度与加速度的连续性与平滑性。Wu等[2-3]对梯形、S型和三角函数等加减速控制算法进行理论研究。梯形速度规划控制算法原理简单、比较易于实现[4]，但规划计算结果速度不够光滑，加速度突变，严重时会导致丢步[5]。S型规划能解决加速度突变，为应对特殊情况下S型曲线使用拉式逼近法来求解完整S型规划[6]，但算法计算量较大，并不适合在一般嵌入式平台使用。三角函数型加加速度轨迹规划要具有更好的边界值控制能力，并且插补曲线更加平滑[7-9]。而提出的梯形与余弦想结合的新型算法内容，提供了一种新的计算思路[10]。在新思路下应用到前瞻处理中，对运动拐点采用新运动公式来设计拐点处的加减速段[11]，但对于算法使用存在限制，在一些特殊条件限制下，规划算法并不能输出想要的结果。为此本文提出一种对新型速度规划进行优化的方法，解决之前方法的局限性，使速度规划算法能更灵活地运用于实际条件，并提高响应速度，对应用该加减速运动规划算法解决工业上要求快速平滑响应的工程问题具有重要的现实意义。

1 新型曲线速度优化原理分析

钟前进[10]提出的新型S加减速算法在对位移积分后，计算公式仍然与梯形加减速一样，如此就大大简化了轨迹规划及速度前瞻时的运算量，从而大大简化了算法，而且运算量相对来说比较小，非常适合嵌入式的运动控制，优化后的位移公式为：

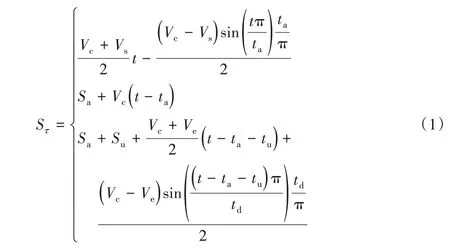
在提出的新型S型加减速规划算法中是以梯形思想为基础进行分析与处理的，在梯形计算过程中核心思想在于根据约束的加减速度计算出运动的最大瞬时速度从而判定梯形规划是两段无匀速运动还是三段有匀速运动，结合实际多段连续短轨迹情况下也可能会存在一些极端加减速情况，比如只有加速段与匀速段、只有匀速段与减速段和只有匀速段的情况，甚至只有减速段的情况。在采用的基于时间与路径例化插补算法中，最重要的就是在每个插补状态对瞬时速度的例化，而例化公式是依据当前瞬时速度对时间与位移的映射关系来确定的，因此本文就是对瞬时速度对时间与位移的映射关系进行求解。对于极端情况下的处理思想采用判断加速运行时间与减速运行时间是否是零即可确定当前运动归类，瞬时速度映射关系则可根据匀速时速度关系式得到。对于不能达到匀速状态的情况则只能加速与减速，本文对不能达到匀速状态的运动实时速度、位移与时间之间的映射关系进行推导，并以此为依据实现在时间轴上的映射。

由于梯形运动是直线加速度运动，满足直线运动速度公式：

式中：Vc为当前实时速度；Va为起始速度；ta为加速运动的时间；Sa为加速运动的位移。

由速度公式可得加速度的关系式为：

根据当前运动过程中直线加速运动速度与位移的关系式可得：

式中：Vc为停止速度；Sd为减速运动位移。

由Sa+Sd=Sp（其中Sp是总位移）和式（2）结合代入公式（4）化简可得加速度关系式：

运动过程中加速度值是一致的，即式（3）与式（5）相等，代入可得速度与时间、位移之间的映射关系为：

上式即为无匀速段运动下加减速值一致时瞬时速度对时间与位移的映射关系式，该关系式适用于加减速的全过程。而当运动过程中加速度与减速度不一致时，则根据运动一般公式可知加速过程与减速过程的瞬时速度映射关系式为：

而对于能够达到匀速状态的运动过程分析就比较简单，在运动规划过程中能够求得匀速运动位移Su与匀速运动时间tu，从而根据位移与速度公式就能求得瞬时速度的映射公式：

2 例化优化算法实现

对于梯形速度规划，对时间进行时间轴映射时默认加减速时间是一致的即对称运动，非对称运动对时间轴例化是不能单一而谈的，在运动规划的一般条件下微小段距离运动规划会比较多，而在实际微小段运动中经过前瞻处理后速度的约束条件会存在比较多的复杂情况，而对于复杂情况下的速度规划不能单一简化，本文提出的思路则是对加速阶段与减速阶段进行单独分析，规划结果以规划能达到的最大速度为连接点与着手点，对加速阶段的瞬时速度进行时间与位移例化，并对减速阶段的瞬时速度也进行时间与位移的例化。本文基于一般非对称运动为核心，给出非对称时间轴例化一般式，如此既能满足对称速度规划也能满足非对称速度规划，在插补过程中，计算的核心就在于求解插补的例化因子λ：

其中起点坐标是(xs，ys)，目标点坐标是(x，y)，为直线运动规划时的插补位移求解公式，若为圆弧运动则插补公式为：

式中：r为圆弧运动的半径；θ为圆弧运动的圆心角；flag为运算符号，由圆弧运动的顺逆方向决定，逆时针时为正，顺时针为负，核心共性都是对插补例化因子λ进行求解。

对插补例化因子的求解步骤如下。

（1）由设定的最大速度求解加速度段位移与减速度段位移以及两段位移之和。

（2）若总位移比步骤（1）求解位移和大则到步骤（5），若总位移等于求解的两段位移和，则说明是刚好达到最大速度，否则需要计算能达到的最大速度。

（3）求加速时间ta、减速时间td、加速运动位移Sa、减速运动位移Sd，并获得例化参数：

此时若加速时间ta=0，则表明运动过程为极端情况，此时没有加速段，则在加速过程中瞬时速度例化为零，此时速度的例化参数为：

式中：Vcaf、Vcdf、Vaf、Vef分别为加速段速度、减速段速度、起始速度、结束速度的例化参数。

若减速时间td=0，此时没有减速段，则在减速过程中瞬时速度例化为零，此时速度的例化参数为：

当起始速度与结束速度相等时，此时运动具有特殊性，但依据加减速运动段单独分析方式，此时速度的例化参数为：

而当起止速度非对称时，结合式（6）可得速度的例化参数为：

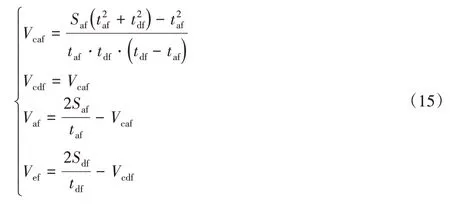
（4）由式（1）作简单变换得到无匀速段梯形余弦计算位移公式，可得优化后的插补例化因子为：

式中：t为当前插补点的状态时刻，且t=,i=1,2,3,…,N，

其中N代表总的插值点数。

通过对总的插值点数进行控制就能间接控制每个时刻的插补点的状态时刻的运动状态，从而实现细分化的插补路径控制，其中插值点数的计算方式为：

式中：C为插值倍增系数，用来倍增插补点数；S为运动总位移或圆弧运动的圆心角；V为运动的线速度或圆弧运动的角速度。

（5）同步骤（3），先求加速时间ta、匀速时间tu、减速时间td、加速位移Sa、减速位移Sd，然后可求得例化参数为：

式中：总位移为满足Sp=Sa+Su+Sd的当前所有轴运动规划的路径总数。

在运动中若加速时间ta=0，则起始速度例化参数Vaf=0，否则起始速度例化参数；而若减速时间td=0，则结束速度例化参数Vef=Vcf，否则结束速度例化参数为Vef=。在求得起止速度例化参数后结合例化参数式（18）并代入式（1）可得插补例化因子为：

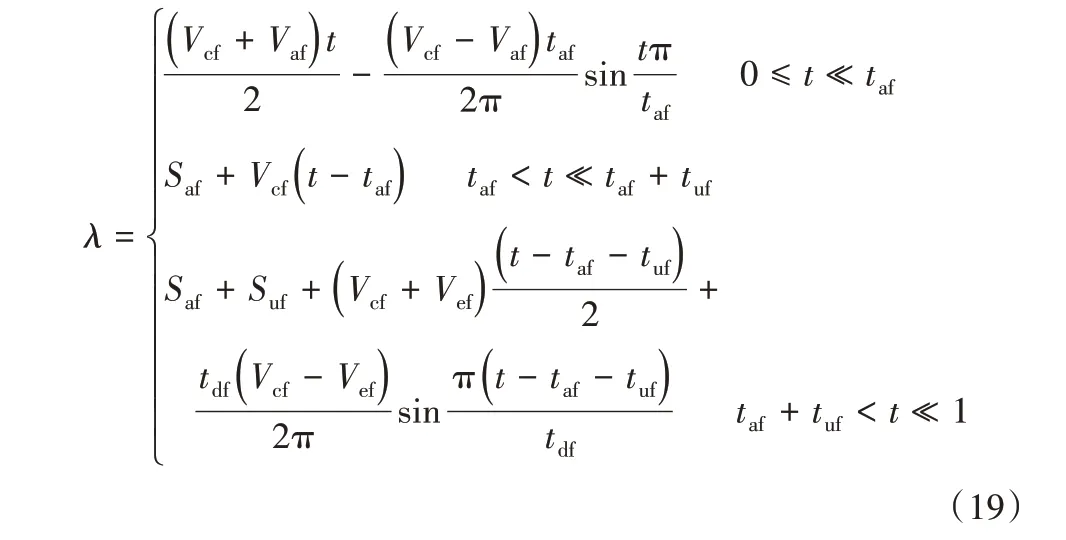
优化后的以上5个步骤流程能将实际情况所有条件下的规划情况都涵盖，在每一个插补点时刻i都会有唯一的插补例化因子与其对应，将例化因子代入式（9）中就能求得在每一个插补时刻点的坐标位置信息，并通过对当前的新型路径因子计算式进行求导就能得到当前的状态时刻的速度，结合对当前路径输出求出当前插补点坐标，细分到每个运动输出上就能得到对当前速度规划应该输出的速度与脉冲个数。

3 实验验证分析

在仿真平台MATLAB上根据以上步骤流程编写算法与测试代码，同时仿真S型规划、梯形规划与优化后的新型S型规划，仿真数据通过验证不同的运行距离，比较3种规划算法的输出曲线，为了让三者能有明显的对比，测试在设计时保证了3种规划算法在插补时具有相同的插补数，这样在每一个插补点的结果是在相同时刻的规划输出。

（1）验证参数数据为Va=0 mm/s，Vc=60 mm/s，Ve=10 mm/s，Sp=100 mm，最大加速度为30 mm/s2。此时梯形速度规划有两个阶段，S型规划分为4段，对应的速度与加速度曲线如图1所示。

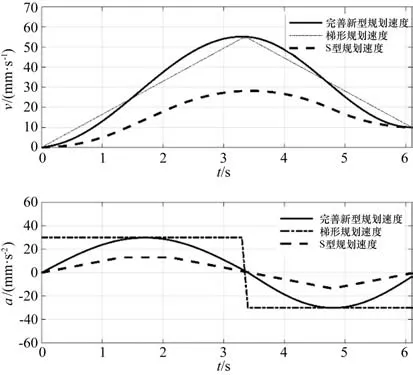
图1 条件（1）速度及加速度曲线

（2）验证参数数据为Va=0 mm/s，Vc=60 mm/s，Ve=10 mm/s，Sp=600 mm，最大加速度为30 mm/s2。此时梯形速度规划有3个阶段，S型规划分为5段，对应的速度与加速度曲线如图2所示。

图2 条件（2）速度及加速度曲线

（3）验证参数数据为Va=0 mm/s，Vc=100 mm/s，Ve=10 mm/s，Sp=800 mm，最大加速度为30 mm/s2。此时梯形速度规划有3个阶段，S型规划分为7段，对应的速度与加速度曲线如图3所示。

图3 条件（3）速度及加速度曲线

由以上3组验证数据的结果图显示，在非对称的一般情况下，优化后的新型速度规划算法都能根据约束条件灵活地计算输出较好的结果，并且在同等约束条件下优化后的算法还能以更平滑的加速度进行更快地响应。

4 结束语

在以速度规划为核心的控制中，被控对象的运动状态要求尽可能地平稳，也就是驱动被控对象的电机输出速度曲线要足够的光滑，运动加减速过程要平滑，不能有突变。为适应可移植运算在嵌入式平台复杂度的运算，并适用于所有运动条件下的运动规划，本文对提出的一种可移植到嵌入式平台的新型S曲线加减速算法进行了优化改进，提升了原算法计算的灵活性，能够适配所有的运动条件进行速度规划，在验证的算法设计结果中，数据表明优化后的新型S曲线加减速算法不仅能输出平滑的速度，还能更快地响应达到最大速度，从而使受控对象能够更好地快速平稳运动到期望位置。