基于PCA-CNN模型的页岩储层有机碳含量预测方法

管倩倩

（中国石化胜利油田分公司勘探开发研究院，山东东营 257015）

随着非常规油气勘探的深入，页岩油气已成为勘探研究的重点，而总有机碳含量（TOC）是影响页岩储层品质的主要因素。总有机碳是单位质量岩石中有机碳的质量，是评价有机质含量的指标之一，因此准确求取页岩储层TOC，对页岩储层评价具有重要意义［1］。济阳坳陷发育富有机质页岩，页岩层系中砂岩、碳酸盐岩等夹层油气规模仅占20%，资源规模最大的油气部分赋存在纯页岩中，所以对烃源岩的TOC进行精准评价是亟待解决的关键问题之一。

目前，获得TOC的方法主要有2大类，一是通过实验测得岩石样品中的TOC，但费用高昂，且实测数据有限，难以推广；二是利用测井资料计算页岩储层的TOC。中外学者提出了很多利用测井曲线计算TOC的方法。刘超等总结前人研究成果，提出改进的ΔlogR法，ΔlogR法主观因素较多，不宜推广［2］；SCHOMKER 在冀中坳陷廊固凹陷发现密度和自然伽马测井值对TOC敏感，利用密度和自然伽马测井资料，可回归计算页岩储层TOC，但适用性不强［3］。目前人工智能方法在处理大数据和预测TOC方面表现出优越性。王惠君等利用CNN，GA-BP 等大数据模型预测TOC［4］。张佳佳等采用Voigt 平均模型和Gassmann 方程进行建模，利用速度反演TOC［5］。LIU 等采用HS 模型、SCA 自洽模型、Backus平均模型以及Schoenberg 线性滑动模型进行建模，对页岩储层TOC等参数进行反演［6］，这些人工智能方法在评价TOC的精度和对复杂页岩储层的适用性上需要进一步提升。

以东营凹陷牛庄洼陷页岩油取心井沙四段上亚段纯上次亚段（Es4上纯上）实验分析TOC数据为基础，采用常规陆相页岩储层TOC计算模型预测TOC，但效果不佳。为此，利用主成分分析（PCA）模型，对数据进行降维，再利用卷积神经（CNN）模型进行TOC预测，形成PCA-CNN 模型，改进后的模型使样本数据质量和预测精度进一步提高。

1 区域地质概况

牛庄洼陷位于东营凹陷南坡东段，呈西薄东厚的不对称箕状洼陷，新生界古近系半深湖-深湖沉积环境，构造相对简单，南部发育一条大的北倾断层，派生多条反向调节断层。牛庄洼陷的内混积带是油页岩夹碳酸盐岩条带，外混积带是油页岩夹砂岩条带［7］。

2 TOC敏感参数分析

一般富有机质烃源岩具有高自然伽马、高声波时差和低密度等测井响应特征。自然伽马偏高是因为地层中存在大量的放射性元素，包括铀、钍等，其中铀元素对有机质有很好的指示作用；有机质密度偏低，导致烃源岩整体为低密度；有机质会使声速降低且成熟的烃源岩存在不易导电的液态烃类，导致声波时差和电阻率变高［8］。

分析实测TOC与页岩油取心井敏感测井曲线自然伽马（GR）、电阻率（Rt）、声波时差（AC）、密度（DEN）、中子（CNL）和孔隙度（POR）之间的相关性。由图1 可知，TOC与AC，DEN，GR的相关性较好，相关系数分别为0.455，0.501 和0.531；其次是Rt，R2为0.189；而POR，CNL与TOC无明显相关性。

3 TOC预测常规模型

近年来，基于测井资料计算TOC的常规模型有很多，较为成熟的方法包括ΔlogR法、多元回归分析法、密度单因素计算模型等。笔者采用常规的ΔlogR法和多元回归分析法预测研究区页岩油取心井牛页1井TOC，建立相关TOC的测井公式。

3.1 ΔlogR法

ΔlogR法将电阻率曲线和声波曲线进行重叠，是目前广泛使用的方法之一［9］。首先对岩心进行深度归位，然后标准化声波曲线与电阻率曲线并计算幅度差，其表达式为：

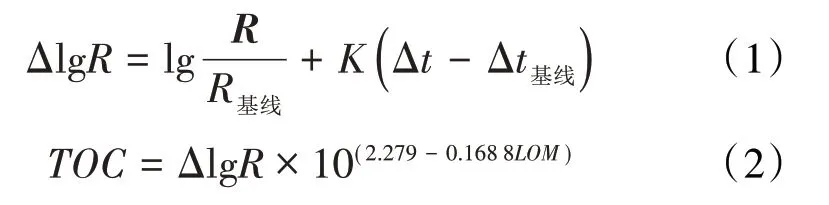
利用（1）—（2）式计算TOC，通过实测TOC与ΔlogR法预测TOC之间拟合得到线性关系（图2）。

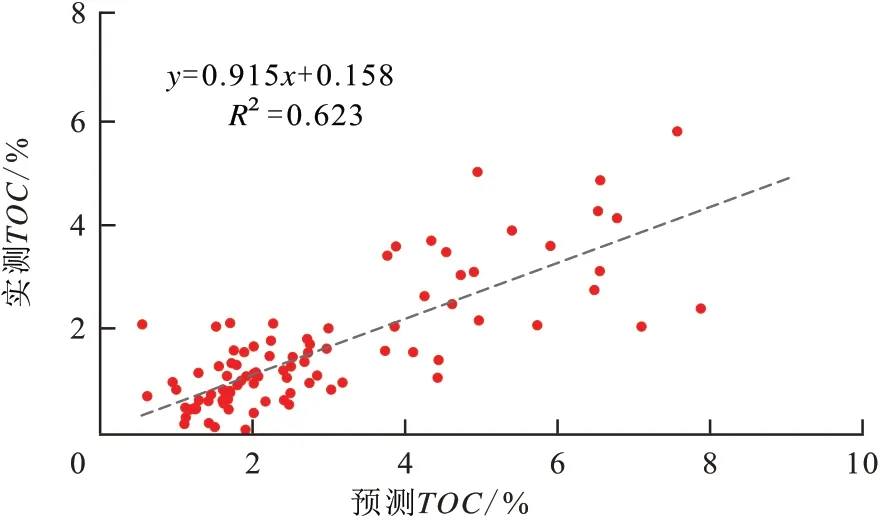
图2 实测TOC与ΔlogR法预测TOC的相关性分析Fig.2 Analysis of correlation between measured TOC and predicted TOC by ΔlogR method

利用ΔlogR法预测TOC，与实测TOC相比，相关性不高，原因主要有2点：①由于成熟度参数借用国外实验参数，对研究区的实验缺少参考依据。②ΔlogR法计算过程中需要人为确定页岩基线等多个参数，误差较大。

3.2 多元回归分析法

多元回归分析法是利用测井敏感参数，建立与TOC相关的多元线性回归方程［10］。根据研究区测井资料单参数数据拟合，TOC与中子、密度和声波时差相关系数较高，与其余测井曲线相关系数较低。因此，选取中子、密度和声波时差作为敏感参数，进行多元回归分析，建立多因素计算模型。其表达式为：

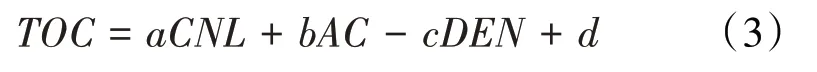
根据最小二乘法拟合获得a，b，c和d值，分别为0.038，0.032，-4.912和14.651，得到多元回归方程：

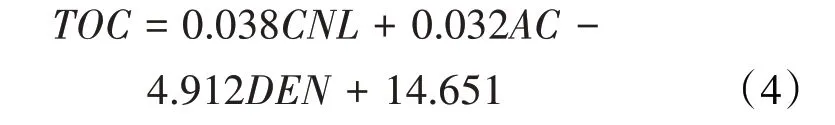
多元回归分析法R2不高，为0.668（图3，图4）。该方法所建立的模型为非理论模型，仅能确定测井响应值与TOC的正负相关性，这种线性或非线性约束存在其不合理性，且在研究区的页岩油井中，与TOC的相关系数不高，因此利用敏感曲线所建立的多元回归模型并不可靠。

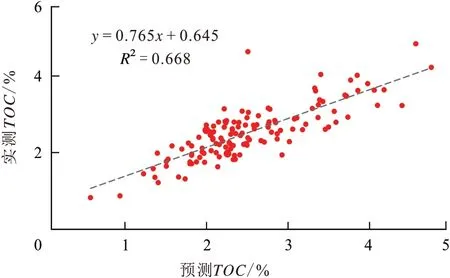
图3 实测TOC与多元回归分析法预测TOC的相关性分析Fig.3 Analysis of correlation between measured TOC and predicted TOC by multiple regression analysis method

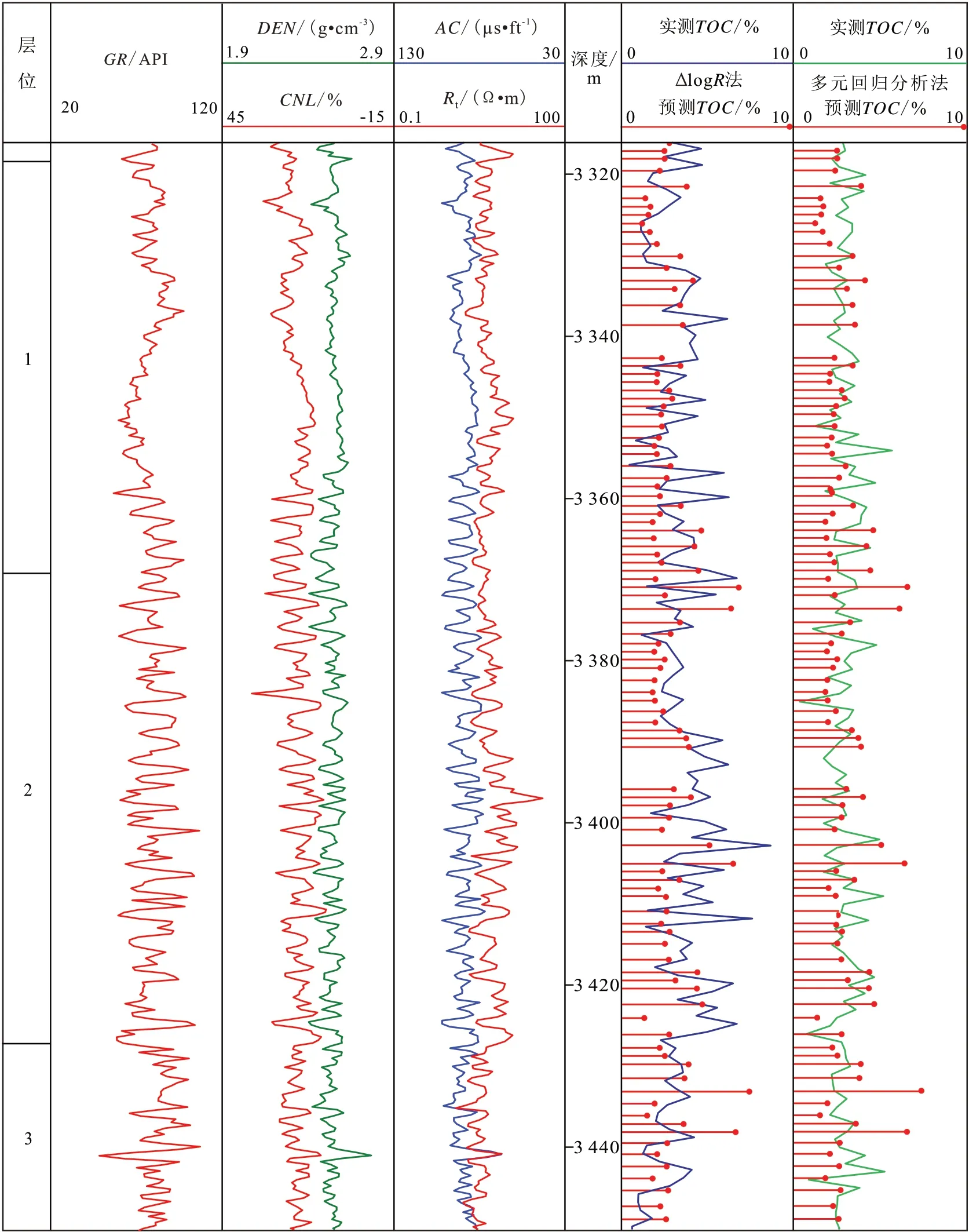
图4 利用多元回归分析法计算牛页1井纯上TOC与岩心实验数据对比Fig.4 Comparison of experimental data of core and TOC calculated by multiple regression analysis method in Upper Chun Submember of Upper Es4 Member of Well Niuye1

4 基于PCA-CNN 模型的TOC 预测方法

页岩储层测井曲线数据里包含冗余信息和噪声信息，会在实际应用中产生误差，影响准确率，而降维可以提取数据内部的本质结构，减少冗余信息和噪声信息造成的误差，提高精度［11］。页岩储层测井曲线数据之间存在多重共线性，即各个测井数据属性之间存在着相互关联关系，具有多重解的可能性，从而导致模型的泛化能力弱；而东营凹陷页岩储层测井数据样本具有稀疏性，导致模型比较难找到数据特征。通过主成分分析法可以减少测井数据中特征属性的个数，确保特征属性之间是相互独立的，同时减少了计算量，缩短训练时长。

4.1 PCA模型

PCA 是一种使用最广泛的数据降维算法［12］。PCA的主要思想是将n维特征映射到k维上，在原有n维特征的基础上重新构造出来k维特征。通过计算数据的协方差矩阵，得到协方差矩阵的特征值和特征向量，选择特征值最大的k个特征所对应的特征向量组成的矩阵，从而实现数据特征的降维［13］。

4.2 PCA-CNN模型

PCA-CNN 是一种深度前馈人工神经网络，是深度学习技术领域中具有代表性的神经网络之一［14］。一个完整的CNN 包括输入层、卷积层、池化层、全连接层和输出层。CNN 与神经（BP）最大的不同在于其增加了卷积层和池化层［15］。卷积层用于提取数据特征，层级之间的神经元为局部链接和权值共享，这样的设计减少了训练的数据量，而池化层用于压缩数据特征，对卷积层输出的特征图进一步抽样［16］。

PCA-CNN 模型即利用主成分分析法计算样本数据的均值向量、协方差矩阵以及特征值、特征向量等，对样本数据进行降维，将新的数据集代入卷积神经网络模型中。具体步骤包括：

①将归一化后的测井数据代入输入层，计算样本数据的平均值、协方差矩阵、相关系数矩阵，以及相关矩阵的特征根和特征向量，表达式为：

②在特征向量中选取m个主分量，当主分量m1，m2，…，mn（m＜n）的方差和占全部总方差的比例接近于1 时，即当m个主分量的方差和占全部总方差的90%以上，说明筛出的样本既可保留主要信息又能充分反映原指标的信息［17］，计算公式为：

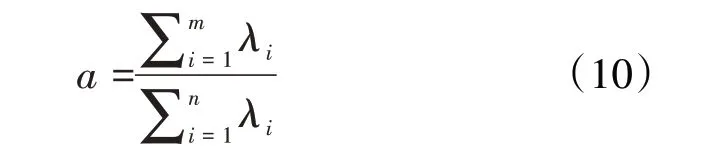
③将利用主成分分析降维后的样本数据代入卷积神经网络的输入层，设置好训练的最大迭代次数，将输入层的数据送入神经网络的输入端［17］。

④设置3个卷积层，利用卷积层提取多个特征，经过Sigmoid激活函数得到输出结果，计算公式为：

⑤利用平均池化降低特征的维度，简化模型复杂度，将卷积层中的数据代入池化层中［18］，预测TOC，计算公式为：

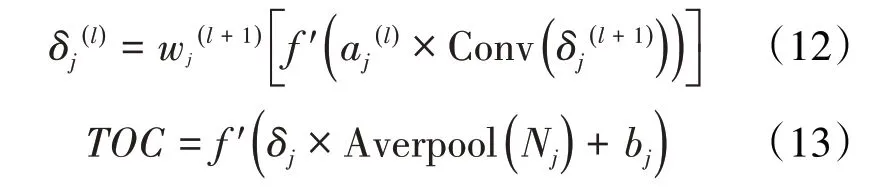
⑥将输出的结果，通过变异系数法对其进行评估，其表达式为：

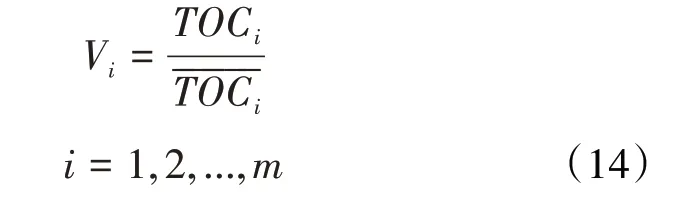
变异系数越小，表示卷积神经网络的应用效果越好［19］。

PCA-CNN 模型在输出层中选用变异系数法输出结果，能够消除平均数不同时对多个样本变异程度比较的影响，可使PCA-CNN 模型的准确率更高。

5 实例应用

5.1 数据的选取及预处理

由于操作不精准或受到地层因素的影响以及测量环境、条件、研究对象存在偏差，从而造成不同井位的岩心深度与测井曲线深度不重合，需要进行岩心归位。通过把岩心深度校正到测井深度上，保证样品数据分析值与地层测井响应特征值一致，确保岩心取样深度与实际深度一致，减少误差，提升数据质量。

对研究区的页岩油井进行测井曲线标准化，选取稳定的泥岩层段作为标准层，利用直方图法对比出误差值，通过统计数据减去误差值，获得标准化数据，消除非地层因素对测井数据的影响，做去趋势化校正，保证测井数据质量。在剔除异常实测值的情况下，利用段对段的方法，将具有TOC的实测值所对应的其他测井曲线在深度上下范围0.5 m 内求取平均值，进一步提高测井数据质量。

5.2 对比及分析

分别用ΔlogR法、多元回归分析法、CNN 模型以及PCA-CNN 模型预测计算TOC，分析4种方法的适用性和精确性。与传统的ΔlogR法和多元回归分析法相比，CNN 和PCA-CNN 模型所预测TOC的精度更高，其中，PCA-CNN 模型的精度最高（表1）。由图5 可知，常规的ΔlogR法在计算TOC时未考虑到研究区岩性的复杂程度，尤其是在黏土矿物和碳酸盐岩含量高的层段预测的TOC值会偏大；多元回归分析法在面对老井测井曲线资料不齐全时无法使用，且针对不同洼陷不同地质构造的页岩油井时，模型并不适用。CNN 模型精度不够的主要原因是前期测井数据处理不够，而PCA-CNN 模型既考虑了研究区岩性复杂导致的测井响应特征不一致的问题，也通过利用PCA 主成分分析法处理测井数据，解决了CNN 模型精度不高的问题，使模型在精度上有了较大提升。

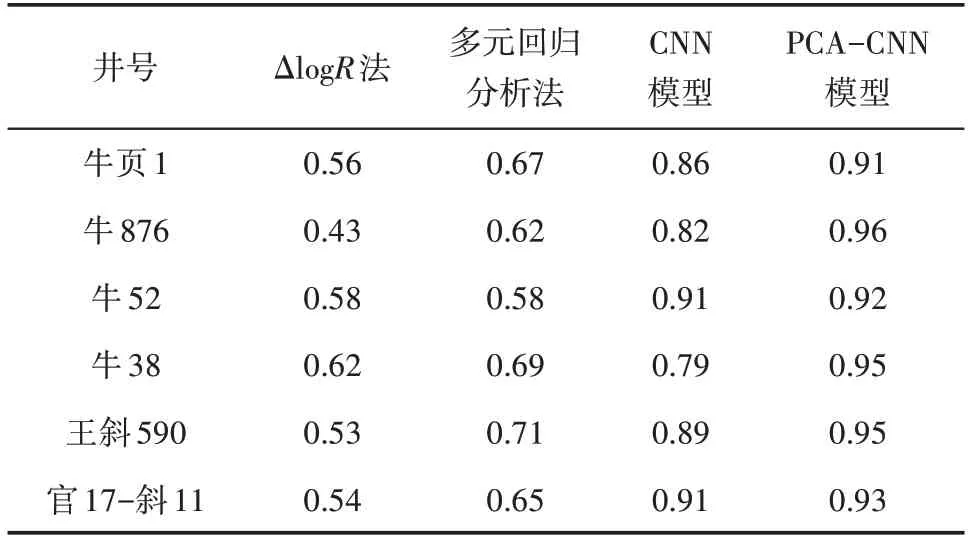
表1 不同算法的R2结果对比Table1 Comparison of R2 under different algorithms

图5 牛庄洼陷纯上不同预测方法结果对比Fig.5 Comparison of results by different prediction methods in Upper Chun Submember of Upper Es4 Member in Niuzhuang Depression

选取牛庄洼陷具有代表性的6口页岩油取心井进行TOC预测和验证，统计232 块岩心实测TOC数据，对测井数据进行主成分分析，减少因测井曲线质量导致的精度降低的问题，然后利用CNN 模型对TOC进行预测，得到牛庄洼陷6 口页岩油井纵向分布的TOC值。如图6，由牛876和官17-斜11两口取心井做对比，牛876 井在牛庄洼陷中心，中间低，四周高，多发育灰质泥岩，而官17-斜11井在牛庄洼陷东北部，处于边缘地带，多发育泥质灰岩，两口井的构造位置和发育的岩相差别很大，但是利用PCACNN 模型计算TOC匹配度较好，精度较高，符合率最高达96%，可见PCA-CNN 模型预测TOC具有一定的推广性。

图6 PCA-CNN模型预测TOC与实测TOC对比结果Fig.6 Comparison of predicted TOC by PCA-CNN model and measured TOC

6 结论

页岩储层具有高自然伽马、高声波时差、低密度的测井响应特征。牛庄洼陷页岩储层TOC与测井曲线敏感参数具有一定的相关性，陆相页岩储层TOC常规计算模型中ΔlogR法和多元回归分析法预测效果不好，采用机器学习模型和PCA-CNN 模型，通过PCA 模型对数据进行降维，再利用CNN 模型进行页岩储层TOC预测，通过PCA改进后的CNN模型使样本数据质量和预测精度进一步提高。对比4种预测TOC模型相关系数，结果表明，PCA-CNN 模型精度最高，稳定性好，应用于东营凹陷6口页岩油取心井，效果好，具有一定的推广性。

符号解释

a，b，c，d——最小二乘法拟合的系数；

aj——经Sigmiod激活函数的输出值；

Averpool——平均池化；

bc——附加偏置；

bj——卷积中的偏置；

Conv——反卷积过程；

E——单位矩阵；

f——卷积函数；

f′——激活函数；

i——输入特征图的总通道数；

j——输出特征图的总通道数；

k——深度点编号；

K——卷积核；

Kij——大小为i×j的卷积核；

l——卷积神经网络结构的层数（本文设置为3）；

LOM——有机质成熟度（热变指数）；

m——主成分的个数；

n——样本总个数；

N——测井数据的列数，即深度点数；

Nj——输入特征图的选择集合；

R——相关系数矩阵；

R基线——非生油的黏土岩中基线对应于基线值的电阻率，Ω·m；

Sii——协方差矩阵；

TOCi——通过PCA-CNN 预测出的总有机碳含量的样本数据集；

Vi——第i项数据的变异系数；

wj——第j个池化权值；

Xki——样本数据；

X′ki——中间计算系数；

yik——时频域参数；

λ——特征值；

λi——第i个主分量的方差，即特征值；

δj——输出层的参数；

ΔlgR——实测曲线间距在对数坐标上的读数；

Δt——实测的传播时间，μs/ft；

Δt基线——非生油的黏土岩中基线对应于基线值的声波时差，μs/ft。