紧扣育人目标 优化作业设计

⦿广东省中山市神湾镇崇正学校 李 悦

《义务教育数学课程标准(2022年版)》[1](以下简称《课标》)是作业设计的依据，它指出数学教育应以“立德树人”为根本任务，面向全体学生，适应学生个性发展的需要，使得人人都能获得良好的数学教育，不同的人在数学上有不同的发展[1].结合《课标》，笔者认为在作业设计上，教师应树立“以生为本”的数学作业观，设置与教学内容有效对接的作业目标，结合学生已有的知识水平和认知规律，选择合适的作业内容，设计科学有效的作业，达到“减负增效”的目的.

1 设计分层作业，激发学生学习兴趣

案例1人教版九年级下册“28.1.1 锐角三角函数”课后作业设计.

(一)作业设计目标.

(1)在解决问题的过程中，能探索发现“当直角三角形的锐角固定时，它的对边与斜边的比值也都固定”这一事实，了解正弦的概念；

(2)能灵活运用正弦的概念进行相关计算；

(3)在作业完成过程中，发展观察、比较、分析、概括等能力，激发学生学习数学的兴趣.

(二)作业设计过程.

优化前的作业设计：

(1)在Rt△ABC中，∠C=90°，AB=2，AC=1，则sinB的值是______.

(2)在Rt△ABC中，∠C=90°，AB=5，AC=4，则sinA的值是______.

(4)如图1，点D(0，3)，O(0，0)，C(4，0)在⊙A上，BD是⊙A的一条弦，则sin∠OBD=______．

图1

(5)如图2，分别求出图中sinA与sinB的值．

图2

(6)如图3，在Rt△ABC中，∠ACB=90°，CD⊥AB，BC=5，CD=4，求sinA的值.

图3

(7)如图4，CD,BE是锐角三角形ABC的两条高，如果CD∶BE=3∶2，求sin∠ABC∶sin∠ACB的值.

图4

优化后的作业设计：

A组：

(1)在Rt△ABC中，若三边长都扩大2倍，则锐角A的正弦值( ).

A．扩大2倍 B．不变 C．缩小 D．无法确定

(2)如图5，分别求出图中sinA与sinB的值．

图5

B组：

(3)如图6，点D(0，3)，O(0，0)，C(4，0)在⊙A上，BD是⊙A的一条弦，则sin∠OBD=______．

图6

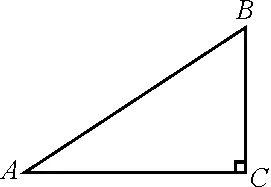
图7

C组：

图8

设计意图：优化后的作业设计，根据学生的认知基础设置了分层作业.A组是基础知识与基本技能层，是面向全体学生的基础型作业，它的设计紧扣作业目标(1)和目标(2)；B组是技能综合应用层，是面向基础中等学生的综合型作业，它的设计紧扣作业目标(2)和目标(3)；C组是能力拓展提升层，是面向基础较好的能力型作业，它的设计紧扣作业目标(3).优化后的作业设计，紧扣目标，指向性强；作业分层，围绕学生，针对性强.优化后的作业设计突出了以生为本的理念，让学生通过“跳一跳”就可以完成学习任务,在完成作业的过程中，学生能够体会到成功感和满足感，达到“减负增效”的目的.

2 设计实践型作业，发展学生学科核心素养

案例2人教版九年级下册“28.2.2 应用举例”课后作业设计.

1.5 统计学处理 采用SPSS 13.0统计软件进行分析。各测量值均以表示，组间比较采用t检验；相关性分析采用Pearson直线相关分析。多组比较采用单因素方差分析(One-Way ANOVA)和Kruskal-Wallis检验分析符合正态分布和不符合正态分布的数据。检验水准(α)为0.05。

(一)作业设计目标.

(1)学生能借助生活中的实例，理解仰角、俯角的意义，并学会正确地判断；

(2)学生经历由实际问题抽象为数学问题(将实物画出平面图形转化为直角三角形)的过程，体会建模的思想方法；

(3)能恰当地选择锐角三角函数的关系式去解决直角三角形中的问题.

(二)作业设计过程.

优化前的作业设计:

(1)如图9所示，课外活动中，小明在离旗杆AB10 m的C处，用测角仪测得旗杆顶部A的仰角为40°，已知测角仪器的高CD=1.5 m，求旗杆AB的高． (精确到0.1 m)(供选用的数据：sin 40°≈0.64,cos 40°≈0.77,tan 40°≈0.84.)

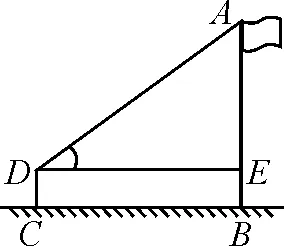
图9

(2)又到了一年中的春游季节，某班学生利用周末到白塔山去参观“晏阳初博物馆”，如图10所示．

图10

下面是两位同学的一段对话：

乙：我站在此处看塔顶仰角为30°；

甲：我们的身高都是1.5 m；乙：我们相距20 m；

请你根据两位同学的对话，计算白塔的高度(精确到1 m).

优化后的作业设计：

运用直角三角形的相关知识，以小组为单位设计测量方案，动手测量学校A座教学楼的高度.(可参考教材第76页练习题、第81页数学活动等.)

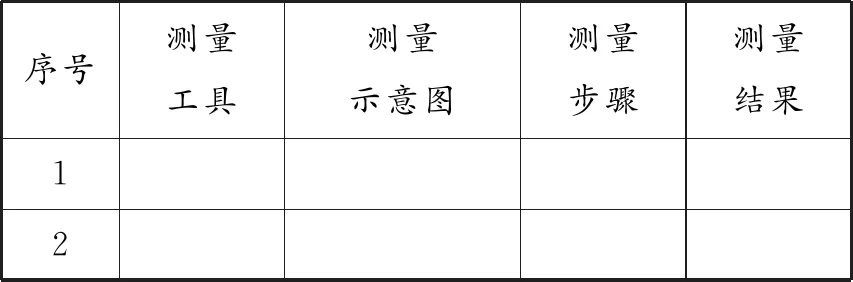
表1 测量表

设计意图：优化后的作业设计紧扣作业目标，依托教材合理选择作业内容.优化后的作业设计是测量教学楼的高度，以小组为单位，商讨方案，做好分工，合作完成.它将教材知识与学生实际生活结合起来，引导学生用数学的眼光观察现实世界(发现可求教学楼的高度)、用数学的思维思考现实世界(思考用学习过的数学知识如何去求教学楼的高度)、用数学的语言表达现实世界(建立模型求教学楼的高度)，培养了学生的建模意识，提高了学生的数学运算能力，发展了学生的学科核心素养.

3 设计个性化作业，促进学生全面发展

案例3“单元练习卷”纠错强化作业.

单元练习是检验单元学习情况的一种有效的方法,除了帮助学生整体掌握数学知识之外，更能暴露出学生的知识漏洞.因此应针对这些漏洞进行查漏补缺，这项工作的完成，对进一步巩固学生的知识有着重要的作用.如何开展实施？以往，教师会让学生将错题抄在改错本上重新做一遍，同时教师再编制针对性练习进一步巩固训练.这样的操作对于知识掌握较好的学生，完成起来比较容易，但是有相当一部分同学完成起来并不容易，他们错的多，不能理解数学知识的本质，这样设计的作业既达不到预期效果，也增加了学生的负担.故在实际操作中笔者设计有针对性、个性化的纠错强化作业，提升复习效率.

表2 纠错强化作业格式

说明：(1)学生将自己能够改正的错题整理在改错本上，简要描述错因(可用红色笔强调)和反思(简要描述以后如何避免)；

(2)在“作业目标”一栏，结合自己错题的相关知识点，填在作业目标处；

(3)强化作业，将老师设计的相应错题的巩固作业条粘贴到“强化巩固”位置，并完成.(提倡自己找1～2题进行巩固.)

设计意图：优化后的作业目标，因人而异，突出作业设计的重点，对以后学习具有指导性.优化后的纠错强化作业设计，提升了作业的针对性、高效性和实效性，培养了学生的批判性思维，减轻了学生的负担，促进了学生的全面发展.

4 优化作业设计建议

“双减”背景下，教师尤其要注意作业设计的优化.笔者认为可以从明确设计目标、创新作业形式、完善作业评价等角度进行作业设计的优化，进而让更多的学生在高质量的作业中夯实基础、提升能力、发展素养.

(1)明确设计目标，夯实基础

目标是教学的指南针，作业设计首先要明确作业设计目标，依托教材，根据《课标》，再选择适合学情的作业内容.这样设计的作业既能减少作业的数量，又能提高作业的质量；这样设计的作业指向性明确，可以帮助学生夯实基础，更好地发挥作业的功能和价值.

(2)创新作业形式，提升能力

单一的作业设计形式会降低学生做作业的兴趣，不利于学生能力的培养，教师要尝试创新作业的形式.数学作业的形式可以有很多种，如：开展数学趣题收集活动、制作数学手抄报、开展数学小课题研究、制作单元思维导图等，这些内容都可以作为数学作业设计的方向.教师通过创新作业的形式，从多个角度为学生能力的培养提供锻炼的机会，达到提升学生能力的目的.

(3)完善评价机制，发展素养

作业评价是作业效果的反馈，传统的评价方式单一乏味，教师批改完作业后写分数(或等级)和日期的居多,这样的评价方式并不能很好地发挥与学生有效交流的功效.实际上，好的作业评价是与学生进行沟通交流的一个重要桥梁，对学生的学习起到一定的促进作用.作业的评价方式还可以从多个角度进行完善，如：教师写鼓励或表扬性的评语，同学之间互相评价，作业展示，作业评比.评价的标准不仅仅是正确率，还可以是书写、态度、整洁度等.作业评价是学生学习的一个重要环节，教师要有意识地完善作业评价机制，达到发展学生素养的目的.

“双减”背景下的数学教学要达到“减负增效”的设计与优化.坚持以生为本的数学作业观，制定明确的作业目标，精选合适的作业内容，促进作业设计的优化，可以激发学生的学习兴趣，减轻学生负担，提升教育教学质量.