借助数学实验 点亮数学课堂

⦿安徽省阜阳市太和县北城中学 田少华

1 引言

面对“互联网+”时代的迎面来袭,特别是在新冠肺炎疫情防控成为常态化的背景下，“互联网+教育”的教学模式自然成为数学教学的应然之举.

《义务教育数学课程标准(2011年版)》基本理念中指出：“数学课程的设计与实施应根据实际情况合理地运用现代信息技术，要注意信息技术与课程内容的整合，注重实效.要充分考虑信息技术对数学学习内容和方式的影响，开发并向学生提供丰富的学习资源，把现代信息技术作为学生学习数学和解决问题的有力工具，有效地改进教与学的方式，使学生乐意并有可能投入到现实的、探索性的数学活动中去.”[1]

纵观数学教学，教师难教、学生厌学，是一个共识的痛点．如何巧妙地在数学教学中融入信息技术，使数学课堂直观化、形象化，是义务教育阶段数学教学迫在眉睫的一个课题.如何借助GeoGebra软件的“动态可视化”，提高课堂效率和学生学习的积极性，提升学生的数学素养，是义务教育阶段数学教学面临的一个课题．为此，笔者做了一些教学层面上的实践，发表一下个人的思考与领悟．

2 课堂教学艺术化、魅力化

传统的数学课堂教学，大多数教师的教学模式都是一支粉笔，一本书，一张嘴，一讲到底，教师只顾着完成教学任务，却忽略了教学目标和教学效果.这就导致了大部分学生觉得数学太乏味，对数学充满迷茫，从而不愿意听课，导致学习效率低下.其实，这些都是可以理解的.因为学生很难在“要我学”的教学过程中转变为“我要学”，从而不能保持注意力集中，自然导致数学教学效果不佳.

数学是有用的，但中学生厌学态势却逐年加强，改变教学的刻板化，“请”信息技术融入数学课堂，是时代之需.基于GeoGebra软件的“3D功能”的动态演示，让静态的知识动态地呈现出来，让学生领悟数学的学习不再是单纯机械地“记公式-套题型”，使学生的身心得以放松，领悟数学知识的魅力，改进“诱”思的方式，读懂数学知识的“玄妙”，调动学生破译数学知识“冷艳”的潜能，促使“探”究的高效性，达到学生的学习与老师的教学有效统一，并有可能投入现实的、探索性的数学实验中去．

如“点动成线，线动成面，面动成体”的学习时，将点设置为“显示踪迹”，在拖动点时，就显示“点”动态地生成直线，再将该直线设置为“显示踪迹”，拖动直线时直线动态地生成平面，若将一个三角形进行旋转，平面自然形成立体图形，借助这种动态的“隐形的翅膀”提供了“玩”数学进行数学实验的空间，这才是最重要的，最有效的．

如讲授圆周角定理时，教师借助GeoGebra软件绘制出圆周角和圆心角的图形，改变图形中A,B,C这三个点的位置，学生会从动画中“看出来”结果：同一段弧所对的圆周角的大小始终是不变的，而且圆心角变化的同时，圆周角也在变化.但是，更为神奇的是“动中有静”：圆周角的大小始终等于圆心角大小的一半，如图1～4.

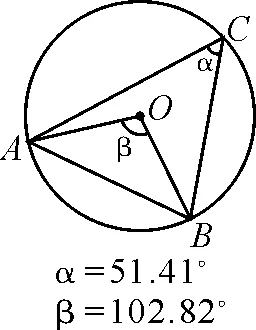
图1

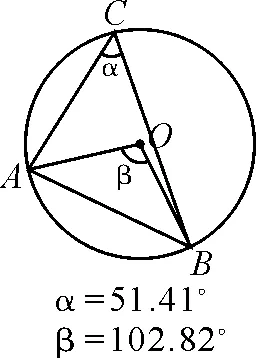
图2

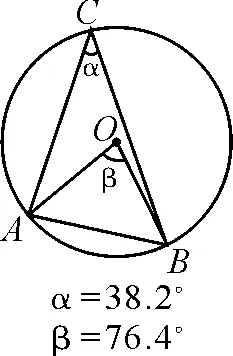
图3

图4

3 教学内容形象化、直观化

数学源于实践，数学中有许多较为抽象的教学内容.遇到这种情况，教师就可以借助GeoGebra软件，在学生已有的认知水平、认知规律和经验基础上，用数学的眼光“看”世界，将原本呆板的知识讲解变为兴趣盎然的“动画”，引导学生积极参与，并关注教学活动中学生的兴奋与迷茫，促使学生积累从具象思维到抽象思维的活动经验，运用数学的抽象意识研析问题、思考问题，进而提升直观想象和数学抽象素养．

如，讲授“图象的平移”时，教师不管如何阐述，哪怕是反复多遍，总有一部分同学迷迷糊糊地，弄不清每个点的坐标如何变化.理不顺左右平移、上下平移中哪一维坐标不发生变化，哪一维坐标发生变化，如何变化，而借助GeoGebra软件的“动态可视化”这些问题就迎刃而解了，学生可以直观地感受图象平移蕴含的内在实质，并主动投入数学学习活动.

4 教学主体参与化、探究化

一节好的课堂，首先要看学生的参与率，能够达到课程标准要求的师生互动、生生互动.其次，还要看课堂上的生成，哪怕是学生错误的想法，都是有用的教学资源.教学需力争做到让学生体验“数学实验”的愉悦感受，历经“感知(数学实验)—初悟(大胆猜想)—思辨(推理验证)—深悟(探究应用)”的过程，学生才会完全掌握知识，甚至可以说一辈子也不会忘记这个知识点，然后再用知识解决问题.

如，在二次函数的教学中，为了使函数知识更加直观易懂，笔者首先了解学生对函数的一些疑问，再使用GeoGebra软件绘制二次函数的图象，如图5，通过拖动a,b,c滑动条，可以形象直观地观察到参数a,b,c的变化对抛物线的开口方向、开阔程度、顶点坐标以及对称轴的影响，还可以发现判别式Δ=b2-4ac的正负与根的个数的联系.这对学生理解函数的图象，掌握函数的性质十分有益.

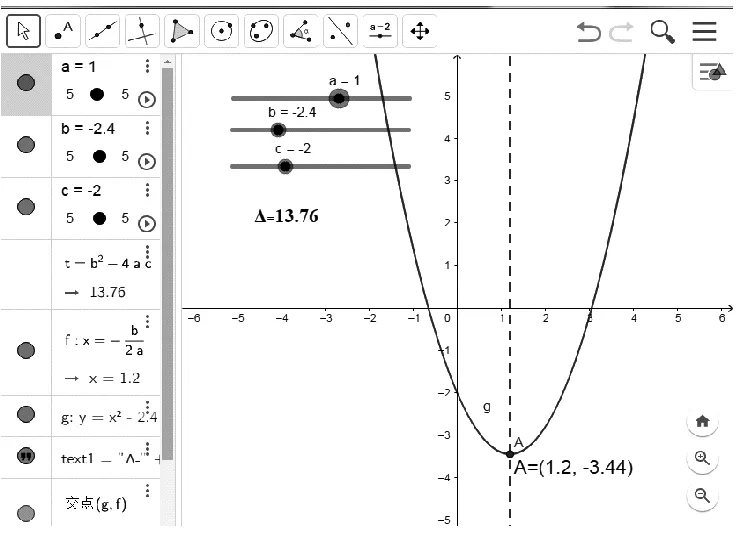
图5

这样一来，“做中学, 学中悟，悟中思”，使课堂呈现的不仅仅是知识的“传输”，而且还是学生感悟“拔节”的声音.

5 数学思维立体化、多维化

“相对于其他数学教育软件而言，GeoGebra软件拥有外观简约，表现力‘强悍’的特点，不仅能直观地‘3D动画’演示立体图形，真实地刻画‘色彩可视’的三维空间，把属于‘只可意会而不可及’的问题，如图形的割补、展开、折叠，将问题‘暴露’得‘迎刃而解’，而且可以借助于绘图区、运算区、表格区等多区域联动表征的优势，把数学模型意识、直观想象素养实现得‘酣畅淋漓’！”[2]

例如，几何体的三视图的教学中，通过“数学实验”就可以得到几何体在三个视角的投影，帮助学生理解并掌握三视图的生成过程，让抽象的几何直观、空间观念变得“活灵活现”，在光影的变幻中，提升学生的空间想象能力.

6 结束语

“章建跃先生在2010年提出了中学数学教学的‘三个理解’，又在2017年将‘三个理解’发展为‘四个理解’，增添了‘理解技术’，这足以说明数学实验的‘可视化’‘动态化’在数学教与学中的重要性.”[3]

依托于GeoGebra软件，请“数学可视化”进入数学课堂，解放了传统教学方式.每一位数学教师应当充分发挥自己的“民间智慧”，选择性地合理使用，真正地“启智润心”，提升学生的数学核心素养.

数学教学的“可视化”之路，还有待且行且探索.