非凸张量多视图子空间聚类

洪振宁,苏雅茹

(福州大学计算机与大数据学院,福建 福州 350108)

0 引言

在实践中,多视图学习有着广泛的应用,传统的机器学习算法,如谱聚类[1],将多个视图串联成一个视图来进行学习.然而这种串联缺乏物理意义,可能导致过拟合.与单视图学习相比,多视图学习引入了一个函数来模拟特定的视图,并联合优化所有的函数,以利用同一输入数据的不同视图提高学习性能.

在实际应用中,高维数据增加了模型训练参数的数量,给硬件带来了计算压力,同时其广泛的数据表现形式,也对鲁棒性提出了挑战.子空间学习采用潜伏的低维特征组合来保留数据的基本信息,从而提高模型的训练效率.子空间学习中最具代表性的工作是低秩表示[2]和稀疏子空间聚类.

然而,这些方法往往具有较高的时间复杂度,并且只对矩阵进行学习.因此,张量结构被引入,探索视图之间的关联[3].考虑到使用的是基于矩阵的奇异值分解(singular value decompostion,SVD)[4],其张量的物理意义并不明确,因此文献[5]使用了具有物理意义的张量奇异值分解(singular value decompostion,t-SVD)代替了矩阵SVD,并引入了张量旋转操作.近年来,为了进一步减少噪声的影响,文献[6-9]将不同的图学习方法与张量结构相结合,即先对输入的特征矩阵进行不同的图学习,再将学习到的矩阵重构为张量.但是仍存在一些不足,如所结合的鲁棒图与联合图不利于处理人脸数据集[6],采用tucker分解与领域自适应增强了聚类效果但忽略了张量的空间特性[7].

以上算法往往使用凸函数来近似张量秩,但这种近似可能不是最优的[10].本研究提出一种非凸张量多视图子空间聚类(nonconvex tensor multi-view subspace clustering,NTMSC).通过非凸函数来近似张量秩,并结合广义奇异值阈值算子(generalized singular value thresholding,GSVT)[11]进行求解,目的是获得更好的聚类结果.

1 非凸张量多视图子空间聚类

1.1 非凸最小化

迭代重赋权核范数(iteratively reweighted nuclear norm,IRNN)[12]被提出来解决以下的非凸最小化问题:

(1)

其中：σi(X)代表矩阵X∈Rm×n的第i个奇异值.函数g:R+→R+是连续的、凹的并且在[0,+∞]上非递增.h:Rm×n→R+是有Lipschitz连续梯度∇的损失函数.

目标函数的一个更紧的替代是保持g的同时只松弛h.然后按如下规则更新,称为广义近端梯度(generalized proximal gradient,GPG) :

(2)

解决式(2)需要引入广义奇异值阈值算子:

(3)

对于满足g:R+→R+,g(0)=0,g是凹的、非递减和可微的且梯度∇g为凸的非凸函数,文献[11]提出了相应GSVT的解法并且证明GPG是收敛的,作为更紧的一个替换,其下降速度优于IRNN.

综上,对GSVT进行求解再根据GPG规则更新即可得到对于非凸最小化问题的解.本研究使用该解法来对张量的秩函数进行近似,并将其应用于多视图子空间聚类问题以提高聚类效果.

1.2 目标函数

本研究提出的非凸张量多视图子空间聚类算法的目标函数如下式所示：

(4)

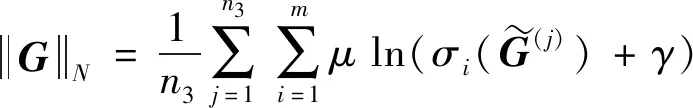
(5)

(6)

其中:α和β为惩罚参数；P和Yi为拉格朗日乘子；T为辅助张量；M代表视图数.〈A,B〉代表内积.

首先对表示矩阵和误差矩阵进行如下更新:

(7)

其中:P(i)和T(i)分别是张量P和T第i个正向切片；(·)T代表矩阵的转置；I为单位矩阵.

(8)

(9)

最后对拉格朗日乘子Yi，以及惩罚参数α和β进行更新:

Yi=Yi+α(X(i)-X(i)G(i)-E(i));α=min(θα,tol)β=min(θβ,tol)

(10)

其中:tol为预先设置的阈值;θ为学习率.

1.3 算法

表1 非凸张量多视图子空间聚类Tab.1 Nonconvex tensor multi-view subspace clustering

2 实验分析

表2 实验数据集Tab.2 Datasets used in our experiments

本实验采用两个不同类型的多视图数据集,具体信息在表2中展示.对于每个数据集,分别采用LRR[2]、t-SVD-MSC[5]、ETLMSC[6]、CGL[9]、RMSC[13]、CGD[14]、CoMSC[15]7种算法进行对比实验.本实验使用6个指标来评价聚类效果:归一化互信息(normalized mutual information,NMI)、准确度(accuracy,ACC)、调整的随机指数(adjusted rand index,AR)、F-score、精确度(Precision)和召回率(Recall).对于所有方法,每个实验均重复10次,最后记录平均值和方差.

图1为满足收敛条件时学习到的相似性矩阵的可视化图像.图2为固定参数λ对参数μ进行调整所对应的指标值变化图像.表3～4 分别记录了本研究方法在6个指标上的聚类表现,其中表3中的数据在λ=0.01且μ=15时取得,表4的数据在λ=1.3且μ=5时取得.

最终相似性矩阵代表各视图所共享的子空间.从图1中可以观察到,学习到的相似性矩阵中多数较大的值都聚集在对角分块上,说明本研究的方法获取到了更丰富的聚类信息,有利于提升聚类效果,表3～4中的聚类结果也证实了这一点.图2表明,式(5)中对于参数μ的引入是有必要的,一个好的μ可以更好地对张量秩进行近似,需注意对于不同类型数据集最优值的区间会有所不同.

从表3～4中可以看出,相比单视图算法LRR,多视图算法t-SVD-MSC挖掘了视图之间的互补性与一致性信息而具有更好的表现.另外对比RMSC和ETLMSC可知张量结构由于探索高维空间关联能加强效果.同时,不同相似性矩阵学习方式对聚类结果也有影响,比如ETLMSC和RMSC均采用基于鲁棒图的转移概率矩阵而在人脸数据集上表现不佳,而CGL构造一致性图并与低秩张量结合明显具有更好的效果.本研究方法对比各算法均有明显提升,不仅由于结合了低秩表示和张量旋转操作,更是因为使用log函数对张量秩进行非凸近似,更好地利用了张量的性质.

图1 相似性矩阵的可视化Fig.1 Visualization of learned similarity matrix

图2 参数μ对聚类效果的影响Fig.2 Clustering result by tuning parameter μ

表3 COIL-20数据集上的聚类表现Tab.3 Clustering result on COIL-20

表4 Extended YaleB数据集上的聚类表现Tab.4 Clustering result on Extended YaleB

3 结语

通过在两个不同类型的多视图数据集上的实验,得出以下结论:1) 多视图聚类算法相对于单视图聚类算法因为探索了多视图间的互补性和一致性具有更好的性能；2) 使用张量结构学习多视图间的空间关联,引入张量旋转操作并使用侧向切片进行实验可以取得相对好的结果；3) 使用非凸方法代替凸优化来近似张量秩可以获取更多视图间的关联信息.