《几何原本》在高中数学教学中的应用

王智洋 韩 粟 (华东师范大学教师教育学院 200062)

1 引言

欧几里得的《几何原本》(下称《原本》)是世界上最著名、最有价值的数学巨著之一，它作为使用过两千多年的教科书，为我们提供了大量数学概念、方法和思想，如今教材中的许多内容均可以在其中找到来源．徐光启曾在《几何原本杂忆》中提到“而习者盖寡，窃意百年之后，必人人习之”，表达了他对于《原本》的赞赏和推崇．在数学文化的价值受到广泛关注的今天，“纯数学”的学习已经不能满足学生的发展需求．教师在当下重温经典，不仅能够获得丰富的教学素材，还能发现其宝贵的育人价值．

随着HPM(History and Pedagogy of Mathematics，数学史与数学教育)得到数学教育界的认可，许多中学数学教师已经认识到数学史的教育价值，但在实际教学中运用数学史仍然存在诸多困难．例如，手头无史料(不知道用什么)，胸中无方法(不知道怎么用)[1]．本文希望结合已有的HPM课例，探究将《原本》[2]中的材料应用于教学的方法，为一线的高中数学教师提供帮助．

2 思想溯源：数学公式的教学

· 等比数列求和公式

《普通高中数学课程标准(2017年版)》(下称《课标》)要求“探索并掌握等比数列的前n项和公式”，国内教材中给出的公式推导方法多为错位相减法，呈现方式也十分相似．错位相减法固然是一种非常重要的思想方法，用途广泛，体现了高等数学中“算法”的思想．但学生在学习中容易产生困惑：为何想到错位相减法？是否存在其他推导方法？[3]

《原本》第9卷命题35中给出了等比数列求和公式的另一种推导方法：

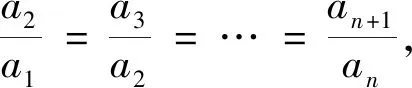
文献[4]第219～226页的课例中教师在引出等比数列求和问题后，通过微视频大致介绍了公式推导的几种思路，引导学生分组进行探究．然后组织学生分享推导思路，展示《原本》中的推导过程以及其他精彩的推导方法．最后让学生运用公式解决古今问题，体会公式的必要性和实用性．

将《原本》应用于教学，为公式的推导提供了一种简单方法——比例法，这种方法与等比数列的定义结合紧密，增添了推导方法的丰富性．学生经历公式推导后了解了比例法思想的历史来源，增加了课堂的人文性．

3 古今对话：几何概念的教学

在概念课教学中，最重要的环节莫过于形成概念并引出定义，学生往往在这一环节缺少同化的过程，只能被动接受．这样得到的概念对于学生而言如空中楼阁一般虚无缥缈，学生不理解定义从何而来，造成概念模糊和混淆．本节以旋转体和棱柱的概念为例，探究《原本》在概念课教学中怎样帮助教师更好地“引”出定义．

3.1 旋转体的概念

《原本》第11卷中分别给出了圆柱、圆锥和球的定义：

·固定一个半圆的直径，旋转半圆到开始位置，所形成的图形称为一个球；

·固定直角三角形的一条直角边，旋转直角三角形到开始位置，所形成的图形称为圆锥；

测试方法：基本站立，1）双手叉腰；2）双手触肩；3）双手在背后；4）双手击掌；5）左手触鼻，右手触摸耳朵；6）双手击掌1次；7）右手触鼻，左手触摸耳朵；8）还原开始时候的姿势。将8个动作依次进行，重复4遍，用时间计算结果。

·固定矩形的一边，绕此边旋转矩形到开始位置，所成的图形称为圆柱．

上述定义都是动态的，与如今教材中给出的具体旋转体的定义基本相同，只是教材中还补充了圆台和一般旋转体的定义．在学习旋转体时，学生容易产生困惑，不理解学习旋转体的必要性，难以想到立体图形的动态形成过程[5].

文献[4]第182～187页的课例中，教师首先通过问题情境展示了生活中的圆柱，并让学生分析圆柱的静态性质，体会学习圆柱的必要性．然后通过回忆圆的静态、动态定义，感受到图形动态定义的生动与活力．接着组织学生利用提供的材料，用图形的运动形成圆柱，从动态角度得到包括“欧氏”定义在内的多种圆柱定义，并引导学生对每个定义进行辨析，强调严谨性．随后通过对多个定义的比较，评选出最优的定义，分享“欧氏”定义的优点和美妙之处．最后将平面图形一般化，得到一般旋转体的定义．

将《原本》应用于教学，从学生熟悉的具体几何体出发，帮助学生抽象出旋转体的概念，感受旋转体的特殊性，对于立体几何的认识从平面过渡到曲面、从静态上升到了动态．学生在动手操作的过程中仿佛穿越时空与古人对话，通过观察不同材料的运动现象产生多种动态定义．

3.2 棱柱的概念

《原本》第11卷中给出棱柱的定义：“一个棱柱是一个立体图形，它是由一些平面构成的，其中有两个面是相对的、相等的，相似且平行的，其他各面都是平行四边形．”“欧氏”定义在历史上很长一段时间里都被认为是棱柱的标准定义，但事实上，通过“正十二面体”的反例，可以说明这个定义是不完备的．

文献[4]第165～171页的课例中，教师先让学生通过观察、搭建模型等方式，从多个角度抽象出棱柱的定义，从而引出《原本》中的定义，并引导学生思考、讨论定义的正确性．然后简单介绍数学历史上对“欧氏”定义正确性的讨论，提醒学生从棱柱的基本量的数量关系和位置关系出发进行思考、动手操作，逐步构造出反例．证明“欧氏”定义的不足后，引导学生通过增加条件来完善定义，最后得到教材上的定义．

教学实践表明，学生对棱柱概念的理解具有历史相似性，他们在学习过程中往往会把棱柱的某些特征放在一起定义棱柱，认为《原本》中的定义是正确的[6]．因此，将《原本》应用于教学中，通过对不完备定义的修正，解决学生对于棱柱的认识从模糊的几何图形过渡到具体的数学定义的困难．在过程中回顾整个棱柱定义的发展历史，让学生感受到数学发展的曲折和探索精神的可贵．

4 方法运用：数学命题的教学

在命题课的教学过程中，教师要让学生经历从命题的背景中发现和提出猜想、推理论证，获得命题的过程[7].《原本》不仅提供了背景素材，帮助教师引出命题，还提供了多种证明方法和思路，帮助学生得到命题．本节以线面垂直判定定理、余弦定理和基本不等式的概念为例，探究《原本》在命题课教学中的应用．

4.1 线面垂直判定定理

《原本》第11卷中给出了线面垂直的定义：“一直线和一平面内所有与它相交的直线都成直角时，则称此直线与平面成直角．”

在同卷命题4中给出了线面垂直的判定定理：“如果一直线在另两条直线交点处都和它们成直角，则此直线与两直线所在平面成直角．”并通过添加辅助线构造全等三角形进行了证明．

教材中给出的线面垂直判定定理与《原本》基本相同，只是在线面垂直的定义中将“与直线相交”去掉，改为“若一条直线与一个平面上的两条相交直线都垂直，则该直线与该平面垂直”．根据前面直线与直线位置关系的内容，教材将《原本》中线面垂直的定义和判定定理进行了简化．因为《课标》中的要求是“归纳出判定定理”，所以教材只是归纳出了定理，没有进行证明，但在实际教学中，仅仅依靠归纳难免会让学生将信将疑．《原本》提供了一种学生可以理解的证明思路，虽然证明过程较为繁琐，但其思路能够启发学生探索其他证明方法．

文献[4]第280-285页的课例中教师首先通过一些生活中线面垂直的例子，如翻开书本直立在桌面上、旗杆与地面等，让学生产生线面垂直的概念，并将生活实例抽象成数学情境，引出“欧氏”定义．然后通过之前学习的直线与直线位置关系相关内容，将“欧氏”定义简化，得到课本上的定义．接着通过分析定义，化无限为有限，得到判定定理．最后展示《原本》中判定定理的证明思路，提示学生添加辅助线，引导学生尝试证明定理．

将《原本》应用于“线面垂直判定定理”教学，在得到线面垂直定义的过程中铺设台阶，先通过几何直观和数学抽象得到“欧氏”定义，再通过简化“欧氏”定义，得到课本上的定义．这给学生提供了证明定理的思路，学生经历了合情推理和逻辑推理的过程，感受到数学来源于生活以及数学的严谨性．

4.2 基本不等式

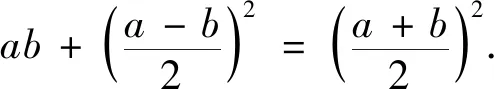
图1 矩形模型

图2 半圆模型

《原本》中的半圆模型从“形”的角度展示了基本不等式的几何意义．在推导基本不等式的众多方法中，作差法是学生容易想到的，也是证明不等式的首选[8]．《原本》中的矩形模型不仅给出了作差法的详细步骤，还提供了几何解释．

文献[4]第338～341页的课例中教师首先通过等周问题引出算术平均数和几何平均数的概念．然后引导学生通过作差法证明，并通过作图比较两个平均数的大小，即《原本》中的半圆模型．接着组织学生尝试通过分析法和综合法严格证明基本不等式．

将《原本》中的两种模型应用于“基本不等式”的教学，帮助学生从“数”与“形”两个角度进一步认识基本不等式，将抽象的代数式变得具体，培养学生数形结合的思想，感受几何图形中蕴含着代数关系的和谐美．

4.3 余弦定理

《原本》第1卷命题47中用面积法证明了勾股定理，这给我们提供了一种思路：将直角三角形推广为一般三角形，用同样的“面积法”证明余弦定理．以锐角三角形为例，证明过程如下：

如图3，在边长为a,b,c的锐角△ABC的三边BC,CA,AB上分别作正方形BCED,ACFG和ABIH．过顶点A,B,C分别作BC,CA和AB的垂线，垂足分别为J,L和N，延长垂线，与DE,FG,IH分别交于K,M和P．

图3 面积法

与勾股定理的情形类似，由于△ACE≌△FCB，则SACE=S△FCB．又SCEKJ=2S△ACE且SCFML=2S△FCB，从而SCEKJ=SCFML．同理可证SBDKJ=SBIPN．那么SBCED=SCEKJ+SBDKJ=SCFML+SBIPN=SABIH-SAHPN+SACFG-SALMG，即a2=b2+c2-SAHPN-SALMG．又因为SAHPN=2S△AHC=AH·AN=c·bcosA=bccosA，且SALMG=AG·AL=b·ccosA=bccosA，所以a2=b2+c2-2bccosA．

另外，《原本》第2卷的命题12和命题13中分别给出了钝角三角形和锐角三角形的三边关系：命题12相当于在图4左所示的钝角△ABC中，有a2=b2+c2+2cm．命题13相当于在图4右所示的锐角△ABC中，有a2=b2+c2-2cm．并利用“作高法”对上述两个命题进行了证明，如图4所示，由勾股定理分别得到a2=h2+(c+m)2=h2+c2+m2+2cm=b2+c2+2cm，a2=h2+(c-m)2=h2+c2+m2-2cm=b2+c2-2cm．

图4 作高法

教材中给出的余弦定理叙述基本一致，将《原本》中的钝角三角形和锐角三角形两种形式合并为三角形式，即a2=b2+c2-2bccosA．但证明方法有所不同，人教版和苏教版教材用向量法证明，沪教版用两点间距离公式．虽然课标中要求“借助向量和运算”，但在实际教学中，学生很难想到用向量方法来解决[9]．《原本》从学生熟知的勾股定理出发，提供了两种证明余弦定理的思路，一种是由面积法证明勾股定理推广到证明余弦定理，另一种是通过构造直角三角形的几何证明方法．

文献[4]第264～268页的课例中教师首先让学生比较不同形状三角形三边和的关系，得到《原本》中余弦定理的描述．然后提示面积法证明勾股定理的思路，启发学生证明余弦定理，并将定理形式合并成课本上的三角形式．接着，教师鼓励学生从代数的角度证明余弦定理，学生想到了作高法、解析法等．最后教师总结方法，并对公式形式进行分析和变形．

将《原本》应用于“余弦定理”教学，不仅为学生从“形”的角度提供了两种证明方法，展示了方法之美，还让学生经历了从勾股定理到余弦定理的类比和推广过程、从几何探究到解析证明的过程，培养研究数学的能力．

5 结语

本文展示了《原本》在高中数学阶段丰富的教学素材，以教材中的“一个公式，两个概念，三个命题”为例，结合相关HPM课例给出了将《原本》应用于高中数学教学中的方法．《原本》中内容、方法和思维的应用，能让学生更自然地理解并掌握新知，构建“知识之谐”；开拓思维，激发创新意识，感受“方法之美”；主动参与课堂，激发学习兴趣，享受“探究之乐”；培养数学抽象、逻辑推理、直观想象和数学运算核心素养，实现“能力之助”[1].同时，它们也帮助教师读懂教材、丰富教学内容，解决实际教学中“概念引入太快”“定理形成过简”“公式推导单一”等问题．

《原本》应用于教学不仅有教学价值，还能够在数学课堂上帮助落实立德树人的教育根本任务．学生在了解相关知识的历史后，能够树立严谨求实的理性精神，培养动态的数学观，在学习过程中仿佛穿越时空与数学家对话，体会数学“冰冷外表”背后的人文关怀，达成“德育之效”[1]．