基于抽象素养培养的变式教学探究——以2018年高考全国卷Ⅰ理科第16题为例

324022 浙江省衢州第三中学 汤小青 陈 旭

变式教学的教学策略包括概念性变式和过程性变式.概念性变式是指构建合适的变异维度，让学生体验学习对象的关键方面，形成对概念的本质理解.[1]过程性变式旨在提供适当的铺垫，帮助学生形成学习对象与已有知识的内在、合理的联系.两种变式策略共存互补、相互促进，分别在不同情境、不同阶段发挥作用.数学抽象素养的形成包含概念、规则的获得，命题和模型的提出，知识结构和体系的形成.通过概念性变式教学，学生能从多角度体验学习对象的数学本质，更好地获得概念和规则；通过过程性变式，学生能更合理地构建知识的内部联系，形成知识结构和体系.因此，变式教学的开展更有利于抽象素养在课堂教学中的落地生根.笔者以2018年高考全国卷Ⅰ理科第16题为例，从变式教学层面进行抽象素养培养的探究.

一、 原题再现

原题(2018全国卷Ⅰ理-16) 已知函数f(x)=2sinx+sin2x，则f(x)的最小值为________.

二、 变式教学设计

为便于不等式的使用，将原题变为以下变式.

变式已知函数f(x)=2sinx+sin2x,则f(x)的最大值为________.

(一)单调性开路

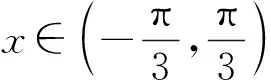
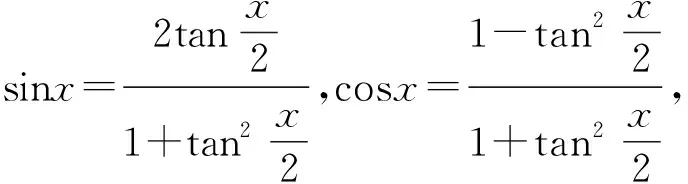
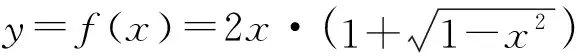
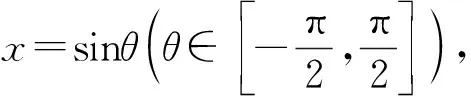
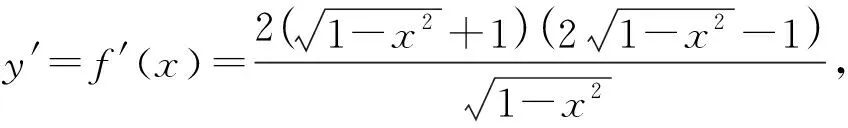
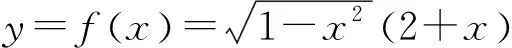
变式2解法与变式1类似，此处略.

设计意图：利用所学知识寻求普适性的方法是解题教学的首要任务.利用导数求解函数单调性，进而解决最值问题，是求解所有可导函数最值问题的通法.从最值的层面更好地构建导数在函数问题中的价值.

(二)应用不等式初探

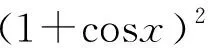
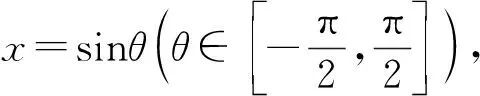
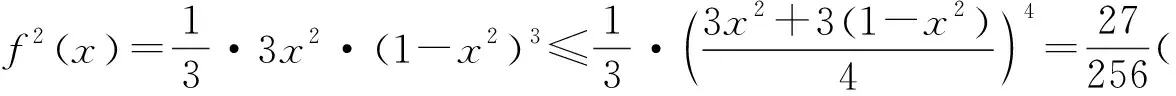
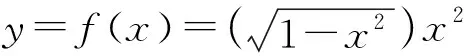
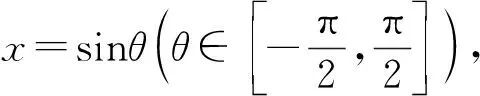
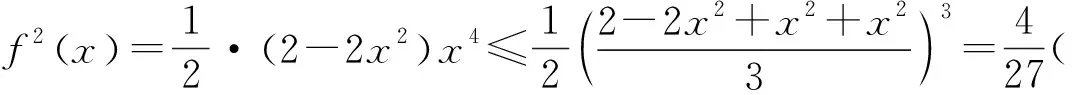
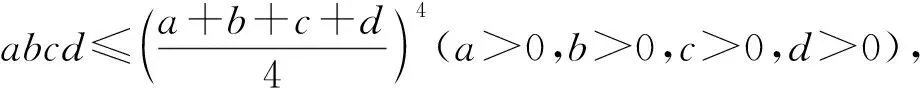
(三)应用不等式再探

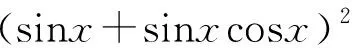
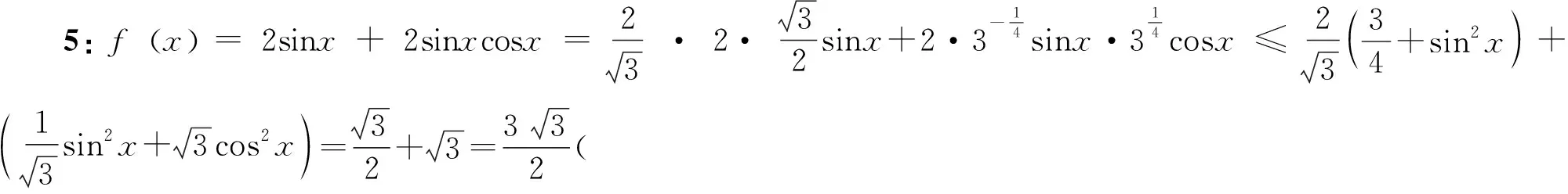
变式5求函数y=f(x)=sinx+sin2x+sin3x的最值.

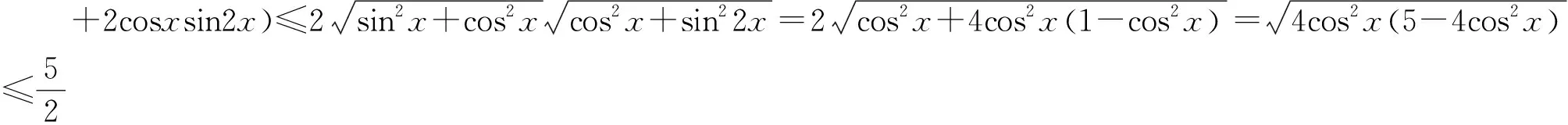
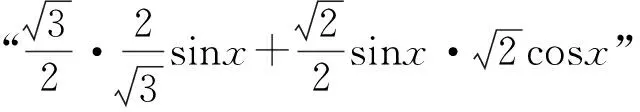
(四)数形结合显威

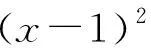
变式6求函数y=f(x)=sin(2x)+2sinx+2cosx+2的最大值.

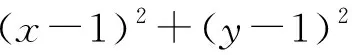
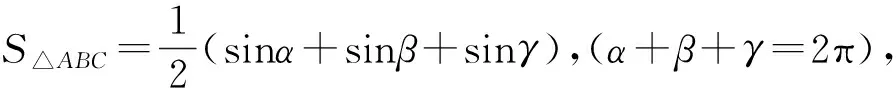
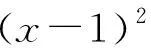
(五)高观点立意

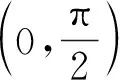
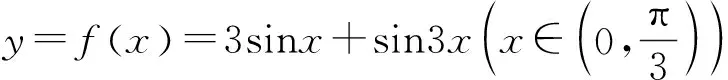
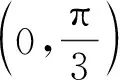
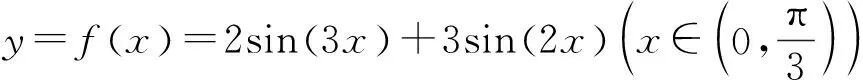
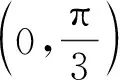
设计意图：2019年人教版高中数学新教材必修一第三章复习参考题中就有“求证：若g(x)=x2+

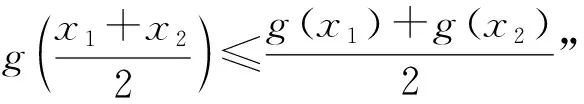
三、 反思与总结

(一)通过变式教学设计完善知识结构，形成知识体系

函数最值问题的知识结构和体系较为复杂，结合三角公式、三角函数可以实现形式的多变性，在多种形式的基础上融合多种方法，进而帮助学生更好地抽象出函数最值问题的知识结构和体系.从通法的角度利用导数研究单调性求最值，结合万能公式，再利用求导求最值；将基本不等式、柯西不等式的形式特点和三角函数的公式变形进行有机结合，让结构的形式和问题的实质相融合；利用问题的结构特征构造反比例函数和圆的相切、构造单位圆的内切三角形面积，让抽象的代数与直观的图形相融合；从函数的凹凸性观点，进一步揭示问题的实质.

(二)通过变式教学设计一题多解，抽象出问题的实质，提升思维品阶

数学核心素养水平的提升，思维能力的进阶，是一个有序的过程.通过合理的变式教学设计、多维度逐层深入的变式，学生经历由通性通法到多种不等式探究、再到数形结合、最后在高观点下立意的探究过程，在逐层深入的过程中逐步揭开问题的实质，不断提升数学核心素养水平，发展高阶思维.

(三)通过变式教学设计多题一解，抽象方法的内涵，形成一般性结论

在变式教学设计中，每一维度都设计多个变式，实现多题一解，使学生多角度认知方法，形成一般性的结论.