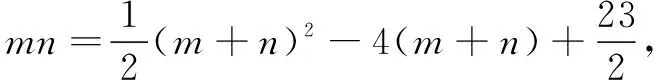中考二次函数模型试题的源与流
石树伟 (江苏省扬州市广陵区教师发展中心 225006)
无论是知识的综合性还是思维的层次性,二次函数都当之无愧地占据着初中数与代数领域的“制高点”,是肩负区分功能的中考压轴题的命题热点.当前,二次函数试题多为“抛物线外衣+几何内核”的命题方式,即以抛物线为背景,将二次函数与三角形、四边形、圆等知识结合起来考查学生的综合应用能力,这样的考查方式“人为拼凑”痕迹严重,掐头去尾烧中段,对二次函数的来源和应用关注不够,偏离二次函数内容的课标要求,对数学建模核心素养的考查缺失.因此,二次函数模型试题应运而生,越来越成为考查热点.
1 认识二次函数模型试题
1.1 从一道试题说起
例1(2013江苏扬州)如图1,在梯形ABCD中,AB∥CD,∠B=90°,AB=2,CD=1,BC=m,P为线段BC上的一动点,且和B,C不重合,连结PA,过P作PE⊥PA交CD所在直线于E.
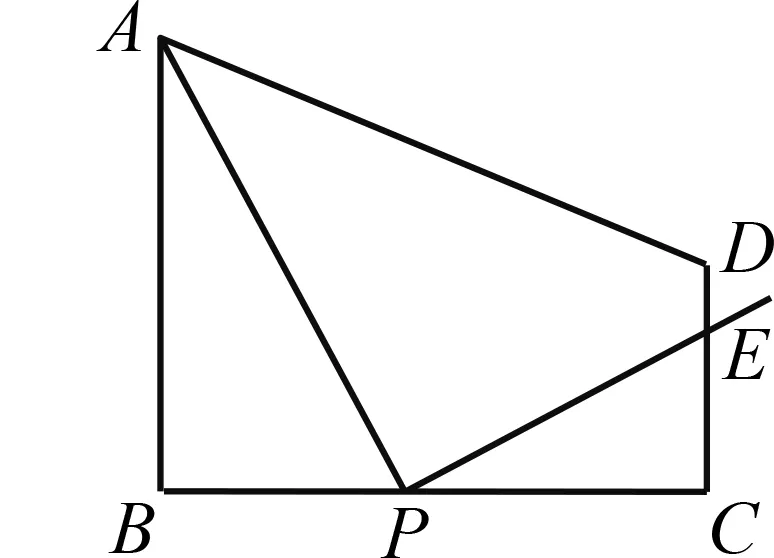
图1
(1)在图1中找出一对相似三角形,并说明理由;(2)若点P在线段BC上运动时,点E总在线段CD上,求m的取值范围.
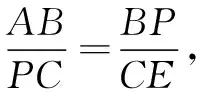
1.2 二次函数模型试题及其考查思路
例1在题目中根本没有出现任何“函数”或“二次函数”之类的字眼,但最终却是用二次函数来解决问题.因为需要学生自己构造二次函数,我们把这类试题称为二次函数模型试题.二次函数模型试题与一般的二次函数试题不同,它关注了二次函数的来源与应用,有利于考查学生的数学建模素养和应用意识.
二次函数模型试题考查的基本思路如图2所示,一般要设计一个现实情境(生活现实或数学现实),因为只有在现实情境中才能考查一个学生“用数学眼光观察现实世界,用数学思维思考现实世界,用数学语言表达现实世界”[1]的能力;一般避免通过小题铺垫来指令学生先构造函数,再利用函数解决问题,而是需要学生自主发现现实情境中存在函数依赖关系,从而自主构造函数,自觉应用函数解决问题.这里强调自主自觉,是因为当学生未来遇到真正的实际问题时,不会再有人告诉他“这个问题里面有函数关系”,或有人替他分解成几个小问题,指令他构造函数.强调自主自觉才能真正考查学生的函数建模意识和能力[2].

图2
2 二次函数模型的源
二次函数模型试题需要学生自主发现函数关系、自主建构二次函数,因此,要想顺利解答二次函数模型试题,首先需了解二次函数模型的一般来路.
2.1 如何想到构造二次函数?
二次函数要靠我们自己发现、自主构造,那怎么想到要去构造函数呢?二次函数模型试题,虽然题目中不会直接指令或提示构造函数,但也不是完全无迹可寻,一般从以下两个层面启示我们要构造函数.
2.1.1显性层面
显性层面,如果试题已知情境问题的最值或研究其最值,可以启示我们想到函数,从而主动构造函数去解决问题.如下面的例2求最大面积,启示学生构造二次函数解决问题.
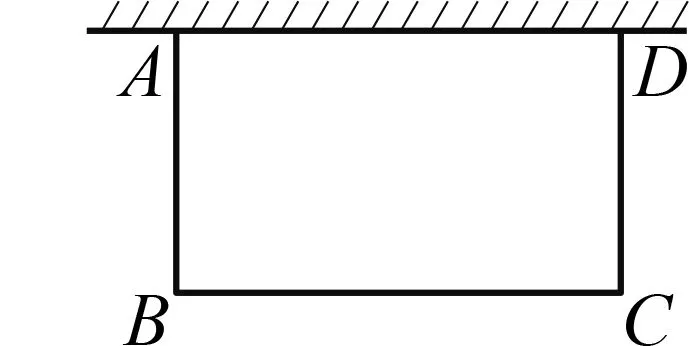
图3
例2如图3,要用总长为16 m的篱笆,一面靠墙(墙的可利用长度为6 m),围成一个长方形的生物园饲养小兔,求小兔活动范围的最大面积.
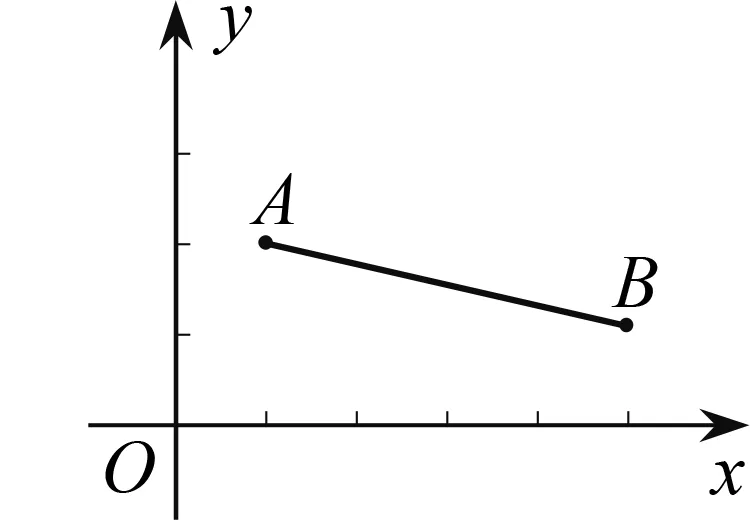
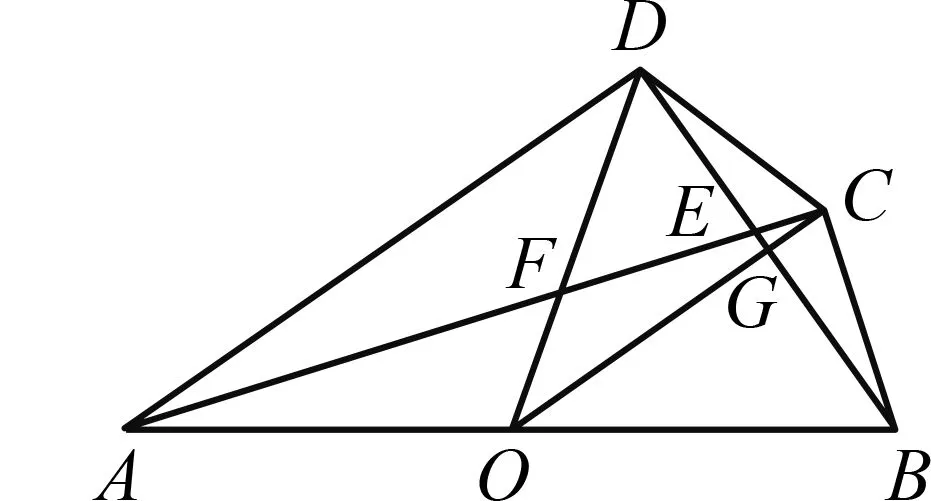
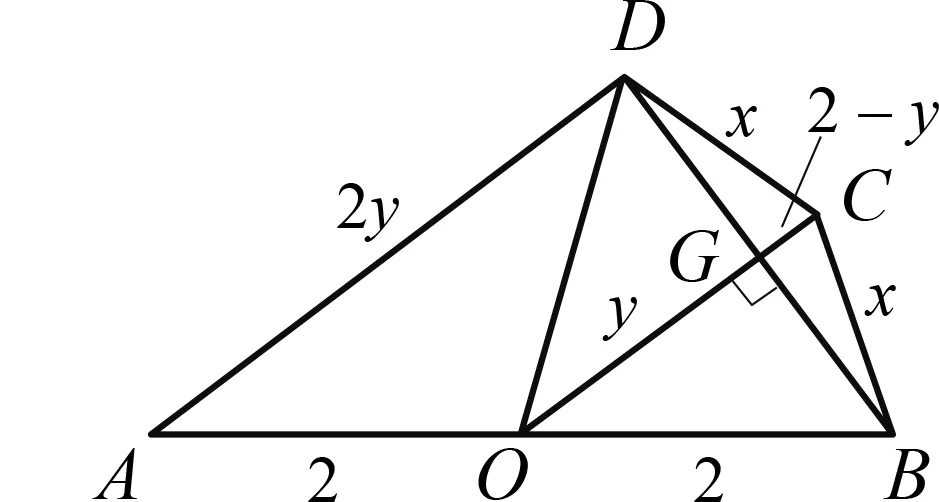
分析 本题求最大面积,容易联想到构造二次函数解决问题.设生物园面积为S,宽AB=x,则长BC=16-2x,利用长方形面积公式可得S=x(16-2x)=-2(x-4)2+32.又因为0 显性层面,如果试题已知情境问题的增减性或研究其增减性,也可以启示我们想到函数,从而主动构造函数去解决问题.如下面的例3,“30天内利润随天数t的增大而增大”,这是已知“利润-天数”函数的增减性情况,启示学生构造函数解决问题. 例3(2016江苏扬州)某电商销售一款夏季时装,进价40元/件,售价110元/件,每天销售20件,每销售一件需缴纳电商平台推广费用a元(a>0).未来30天,这款时装将开展“每天降价1元”的夏令促销活动,即从第1天起每天的单价均比前一天降1元.通过市场调研发现,该时装单价每降1元,每天销量增加4件.在这30天内,要使每天缴纳电商平台推广费用后的利润随天数t(t为正整数)的增大而增大,a的取值范围应为. 2.1.2隐性层面 有的试题虽然没有出现任何提及“函数”的字眼,也没有最值、增减性等方面的显性提示,但通过对问题情境的分析,发现其中蕴含着函数的三个要素:一是在一个运动变化过程中,二是有两个变量,三是一个变量随着另一个变量的变化而变化.由此可以启示我们想到函数,从而主动构造函数去解决问题.如例1是一个点P从点B运动至点C的变化过程,其中BP,CE是变量,且CE随着BP的变化而变化,这就说明CE与BP之间存在着函数关系.这样的函数考查有利于学生充分感悟函数概念的本质,可以让学生体会到函数来源于运动变化过程中变量之间的依赖关系,感悟到函数是研究运动变化过程的有效模型.再如下面的例4. 图4 (1)当n=1时,①求线段AB所在直线的函数表达式;②你完全同意小明的说法吗?若完全同意,请说明理由;若不完全同意,也请说明理由,并求出正确的k的最小值和最大值. (2)若小明的说法完全正确,求n的取值范围. 想到函数了,如何构造函数呢?二次函数的构造,关键在于“二次”如何得到,一般有以下三个途径. 2.2.1乘法模型——一次乘一次得二次 乘法模型“一次乘一次得二次”常见的问题情境有:①面积问题,矩形面积=长×宽,三角形面积=底×高÷2,如果长、宽或底、高都能用含有自变量的一次式表示,则容易得到关于自变量的二次式,如 例2;②销售问题,总价=单价×销量,总利润= 单件利润×销量,若单价、销量或单件利润、销量都能用含有自变量的一次式表示,则容易得到关于自变量的二次式,如例3;③相似问题,相似三角形对应边成比例,若比例外项或比例内项都能用含自变量的一次式表示,则容易得到关于自变量的二次式,如例1;④其他蕴含乘法数量关系的问题,如例4中反比例函数的系数k=动点横坐标×纵坐标. 2.2.2几何模型——运用勾股定理得二次 几何模型“运用勾股定理得二次”常见的问题情境有以下两种: ①一个直角三角形,先用含有自变量的一次式表示各边,然后运用勾股定理得到一个等式,最后展开变形得二次函数,如下面的例5. 图5 (1)若四边形PMCN的面积为3.5,求四边形PMCN的周长; (2)求四边形PMCN面积的最小值,并说明此时点P的位置. ②两个共边直角三角形,先用含有自变量的一次式表示其余各边,然后在两个直角三角形内分别运用勾股定理表示出共边的平方(算两次),得到一个等式,最后展开变形得二次函数,如下面的例6. 图6 例6(2020江苏扬州)如图6,已知点O在四边形ABCD的边AB上,且OA=OB=OC=OD=2,OC平分∠BOD,与BD交于点G,AC分别与BD,OD交于点E,F. 分析 第(1)题易由基本图形“等腰三角形(△OAD)+顶角外角平分线(OC平分∠BOD)”得到OC∥AD,也易由三角形中位线定理(OG是△BAD的中位线)得到OC∥AD. 图7 2.2.3组合模型——多个已知函数组合得二次函数 (1)当科研所到宿舍楼的距离x=9 km时,防辐射费y=万元;a=,b=; (2)若每公里修路的费用为90万元,求当科研所到宿舍楼的距离为多少千米时,配套工程费最少?(3)略. 构造出二次函数关系式不是最终目的,最终目的是为了应用二次函数去解决问题.因此,要想完整解答二次函数模型试题,还需要把握二次函数模型的一般去路. 二次函数模型试题构造出二次函数后,一般应用所构造的二次函数研究以下三类问题.需要注意的是,研究每一类问题都需结合大致图象,即数形结合. 3.1.1研究最值问题 最值问题有三种情况: ①顶点最值,即图象顶点在自变量取值范围内,顶点纵坐标即为函数最值,如例4第(1)题、例5、例6、例7; ②区间最值,即图象顶点不在自变量取值范围内,需结合图象确定最值,如例2; ③离散最值,即函数图象不是连续抛物线,而是一系列的散点,需结合图象根据散点到对称轴的距离远近确定最值. 3.1.2研究增减性问题 增减性问题有两种情况: ①连续抛物线,所有点要保持统一的变化趋势,一般无需考虑跨对称轴的情况,如例4第(2)题; ②离散抛物线,所有点要保持统一的变化趋势,最后一点或第一点可以跨对称轴,与其余各点分置于对称轴的两侧,但跨对称轴的那一点必须最接近对称轴,如例3. 3.1.3研究参数范围问题 这一类问题与前面两类问题有交叉.含参数的二次函数解析式,既含自变量又含参数,因此不能利用它去列不等式求参数范围.一般需表示出它的最值或对称轴,这样就剥离了自变量,仅保留参数,然后再根据已知条件,利用最值或对称轴的范围列不等式求出参数范围,如例1、例4第(2)题. 3.2.1整体的眼光 3.2.2转化的思想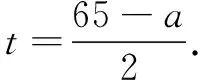
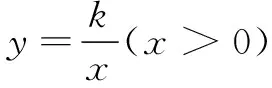
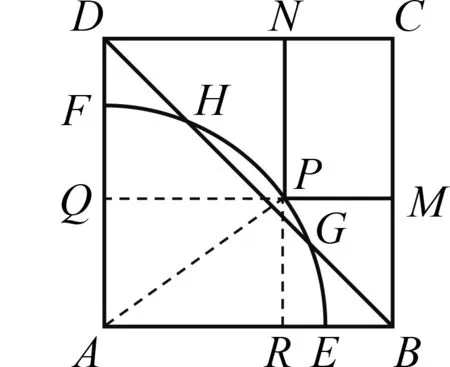
2.2 如何构造二次函数?

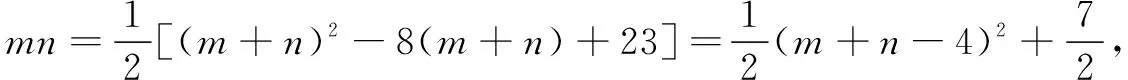
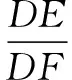
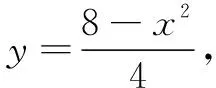
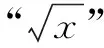
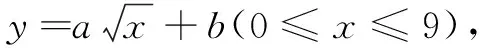
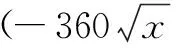
3 二次函数模型的流
3.1 构造的二次函数一般用来干什么?
3.2 构造的二次函数一般有哪些变形?