高压换流站交流滤波器组相干噪声源声功率反演*

赵亚林 路 达王 绿申 晨杨 彬陈 玉杨坤德

(1国网陕西省电力公司电力科学研究院 西安710100)

(2西北工业大学航海学院 西安710072)

0 引言

高压换流站的噪声治理是当前电网环境保护问题中的热点之一[1-6]。交流滤波器场包含大量滤波电抗器、滤波电容器等设备，这些设备在运行时产生的噪声是高压换流站内重要的噪声来源。准确获取噪声源声功率，对于交流滤波器场噪声预测和换流站噪声治理方案的制定都具有重要意义。然而准确获取换流站内噪声源的声功率存在着诸多困难。一方面，设备厂家提供的声功率参数一般在实验室测量得到的，实验条件和运行环境等与实际工况往往不一致。另一方面，当设备处于投运状态时，现有声功率测量方法几乎无法实施。

针对声源声功率难以直接获取的问题，人们提出了参数反演技术，通过实测数据与声学模型的计算结果对比分析来获得噪声源参数。目前，反演方法已应用于交通噪声的计算[7-9]。张景晨等[10]利用经验与半经验模型将建立了一个关于噪声源强度的线性方程组，采用Tikhonov正则化算法求解，得到高压换流变压器的声功率。经验与半经验模型主要基于ISO 9613-2标准[11]，该模型本质上是几何声学理论和实验结果相结合的经验性公式，由于计算相对简单，目前主流的噪声预测软件，如Sound Plan[12]、Cadna/A[13]均采用了该模型。然而经验与半经验模型给出的是声压级结果，相位信息已被消除，因此无法应用于相干噪声源的声功率反演。

交流滤波器组辐射声场是典型的相干声场，不仅A、B、C三相滤波器的辐射声场之间存在相干性，单相滤波器内电抗器与电容器的辐射声场之间也存在相干性[14]。相干性使得辐射声场能量分布存在同相叠加的局部极大与异相相消的局部极小值。因此对于相干噪声源的声功率反演，不仅需要考虑噪声源的强度，还需要考虑噪声源之间的相对相位。几何声学理论将空间中的声场分布视为沿不同路径传播声线的贡献总和，具有直观的物理含义，且能考虑声源的相位信息，在输变电工程的噪声计算方面也得到了广泛的应用[15-17]。本文采用几何声学理论对交流滤波器辐射声场进行建模，分析了相干声场的空间分布特性，建立了相干噪声源声功率反演模型，并通过数值仿真和实验数据对该方法进行了验证。

1 基于几何声学理论的交流滤波器声学模型

1.1 半自由空间点声源

考虑一个由空气和大地组成的半自由空间(图1)，空气中声速为c1，密度ρ1，地面声速为c2，密度为ρ2。当位于rs=[xs,ys,zs]T的点声源以频率f向外辐射简谐声波时，测点r=[x,y,z]T处的声压是直达波和地面反射波相干叠加，

图1 半自由空间点声源Fig.1 Point source in half space

式(1)中：g(r,rs)为半自由空间中点声源的格林函数，w为与声源强度有关的声压系数，决定了点声源的声功率，k=2πf/c1为波数，Ld为直达路径长度，Lr为反射路径长度，ξ为地面反射系数，θ表示发生地面反射时的入射角，且有

1.2 电容器塔声学模型

电容器塔由大量电容器单元按一定方式组成，通常为多层结构，每层包含多个电容器单元，此外还包括附属的支撑结构，如图2所示，其中电容器单元尺寸不超过0.3 m×0.3 m×0.6 m。目前在对整个换流站进行噪声预测时，为了建模的方便和计算的高效，普遍是把电容器塔模拟成单个竖直的线声源[1,15,18]。2020年8月，中国电力企业联合标准会颁布了《塔架式电力电容器装置噪声计算导则》(征求意见稿)[19]。导则将每个电容器单元等效为自由空间中的点声源，给出了单个电容器塔装置声压级的工程计算方法，同时也指出在地面反射较强时，为方便工程计算，可认为噪声声压级较自由场时增加6 dB。这种工程近似忽略了地面反射引起的相位变化，不能直接用于计算多个电容器塔的相干声场。

图2 电容器塔Fig.2 Capacitor tower

本文采用类似的方式，将每个电容器单元等效为一个点声源，但为了更精细地处理地面反射，采用半自由空间点声源模型来计算测点处声场。严格意义上的点声源是指半径远小于声波波长的脉动球源。在实际应用中，当测点距离相对于声源尺寸较大时，也可使用点声源近似。声速340 m/s时，500 Hz声波的波长为0.68 m。电容器单元的尺寸相对于该波长较小，如果测点距离电容器单元较远时，可认为点声源近似是合理的。

由于电容器单元相同，且运行中的电压电流相同，可以认为每台电容器单元的声学特性相同。假设电容器塔中共有N个电容器单元，每个电容器单元的声压系数均为wC，第n个电容器单元的位置为rn=[xn,yn,zn]T，则整个电容器塔辐射到测点r处的声压为

1.3 电抗器声学模型

干式空芯电抗器大致为圆柱体结构，如图3所示，其中较大的电抗器直径为1.7 m，高度为1.6 m。尽管有研究表明电流激励下的电抗器表面振动并不均匀[5]，但是在工程计算中当测点距离电抗器较远时，仍然将其简化为点声源来处理。此外，相比电容器塔，电抗器体积相对较小且结构简单，对交流滤波器场噪声的影响没有前者显著。本文为了建模和计算的方便，将电抗器作为点声源处理。令电抗器的声压系数为wL，等效声中心位置为rL，则其辐射到测点r处的声压为

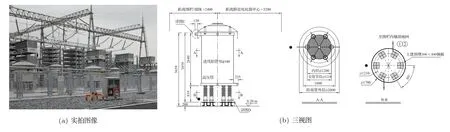
图3 电抗器Fig.3 Reactors

1.4 交流滤波器组声学模型

交流滤波器组包含A、B、C三相滤波器，单组滤波器之间配置完全相同，仅流经电流的相位不同。由于三相滤波器的流经电流相位差恒定，而辐射噪声主要由谐波电流激励下设备振动引起，因此三相滤波器的辐射声场之间也具有恒定的相位差，是典型的相干声场。以单组滤波器为例，图4给出了单相滤波器的等效电路图，包含高压滤波电容器C1、低压滤波电容器C2、高端电抗器L1、低端电抗器L2和电阻器R1。由于电阻器R1和低压滤波电容器C2的噪声较低，可以忽略不计，本文仅考虑高压电容器C1、电抗器L1和L2的噪声。

图4 单相滤波器等效电路图Fig.4 Circuit diagram of the AC filter

假设电抗器的中心位置坐标分别为rL1和rL2，声压系数分别为wL1和wL2。电容器C1含有N个电容器单元，其中第n个电容器单元的位置坐标为rC1,n，则单相滤波器在测点r处产生的总声场为

式(4)中：φ1和φ2分别表示电抗器L1和L2相对于电容器C1的相位差。式(4)可进一步简化为

式(5)中：w表示声压系数向量，g表示格林函数向量，均为长度为N+2的列向量，且有

三相滤波器在测点r处产生的总声压则为

式(6)中：g=gA+ej2πq/3gB+ej4πq/3gC，gA、gB和gC分别为A相、B相、C相滤波器等效声源模型对应的格林函数向量，q∈{-1,0,1}分别表示三相滤波器之间的相位关系是负序、零序或正序。

对于空间中的M个测点，则有

式(7)中：y=[y(r1),···,y(rM)]T表示测点数据向量，G=[g1,···,gM]T表示格林函数矩阵。

需要说明的是，式(7)是一种频域信号模型，它表示某一时刻测点处的复声压。采用复声压为参数进行建模的优势在于不仅可以考虑各相滤波器之间的相干性，而且可以考虑同一相滤波器内不同点声源之间的相干性。理论上，如果已知G可采用求逆的方式进行噪声源强度的反演，然而这要求测点的数据是同步测量的。对于由非同步测量得到的测点数据，则无法使用求逆的方式进行反演。实际上，在设备工况不变的情况下，可认为测点处的噪声功率在测量期间保持恒定。因此反演问题即为在已知的条件下，求声压系数{wL1,wL2,wC}和相位因子{φ1,φ2}。

2 噪声源声功率反演方法

第1节中基于点声源近似建立了电容器塔和电抗器的等效声学模型。在该模型下，它们的声功率与点声源的声压系数直接相关。一旦求得点声源的声压系数，则可以通过附录A中给出的电容器塔和电抗器声功率计算公式求得两者的声功率。下面介绍噪声源声功率的反演方法。

2.1 代价函数与优化算法

令zm=[|y1|2,···,|yN|2]T表示模型(7)的计算结果，zd=[|~y1|2,···,|~yN|2]T表示实测噪声数据，为了从已知的多个测点的数据中求解点声源声压系数和相位，构建如下代价函数：

式(8)中：|·|2为求2范数算符。代价函数f描述了两组数据之间的相关系数，在几何意义上表示高维空间中从原点出发的两条向量之间的夹角。此外，利用实测数据与模型计算结果的绝对差值可构造如下代价函数：

这也是反演问题中常用的代价函数，在几何意义上表示高维空间中两点的欧氏距离。一般而言，基于相关系数的代价函数f比基于绝对差值的代价函数f2具有更好的抗误差能力。

使代价函数值最小的一组参数即为待求的声压系数参数。代价函数的寻优过程可使用全局优化算法实现，本文使用模拟退火算法[20-21]进行寻优。

2.2 反演流程

对于代价函数f，反演流程如下：

(1)对交流滤波器相干声场进行测量，选择合适的坐标原点，将测点位置坐标记为

(2)基于交流滤波器CAD厂址图和建筑几何尺寸(或者实测的几何关系)确定待测噪声源的位置坐标

(3)由式(1)计算点声源位置和测点位置两两之间的格林函数，生成格林函数矩阵G；

(6)多次重复步骤(4)～(5)，统计的分布；

对于代价函数f2，反演流程中步骤(5)可以略去。这是因为相关系数的代价函数在构造过程中进行了归一化，因此需要一个幅度校准的过程。

3 数值仿真与实验数据分析

3.1 交流滤波器场的噪声分布

考虑如表1所示的电抗器和电容器的中心坐标和等效声学尺寸，其中电容器塔沿高度方向为7层结构，层内沿x轴方向为2列，每列沿y轴方向含12个电容器单元。整个电容器部分的尺寸为2 m×3.7 m×7.4 m，这也是主要的发声部分。

表1 交流滤波器组5664设备位置坐标Table 1 Equipment positions of AC filter group 5664

假设环境参数为：空气声速340 m/s，空气密度1.29 kg/m3，大地声速2900 m/s，大地密度3000 kg/m3。图5给出了声源频率500 Hz时，按照表2中的参数计算得到的声场分布情况。其中，图5(a)和图5(b)分别表示A相滤波器组C1高压塔和C1低压塔的声场，图5(c)和图5(d)分别表示电抗器L1和L2的声场，图5(e)表示整个A相滤波器组的声场，图5(f)表示A、B、C三相滤波器组的相干合成声场。可以看出，单个电容器塔的声场具有很强的指向性，且由于电容器塔每层都沿y轴密集排列了12个电容器单元，在垂直y轴的方向上的指向性尤为明显。对于电抗器，由于考虑了地面的影响，电抗器的声场分布在近距离存在环状的极小值点，且极小值出现的位置与声源距离地面的高度有关。经过相干叠加后，单组滤波器的声场以及整个三相滤波器的声场分布变得尤为复杂，在图5(f)中的x轴正方向上甚至出现了声压级显著升高的现象。尽管这里采用的声源参数与实际中的情况不一定相符，但至少从侧面说明了交流滤波器场相干噪声场分布的复杂性。

表2 交流滤波器等效声源参数Table 2 Source parameters of the AC filter

图5 声场分布(500 Hz)Fig.5 Sound pressure level distribution at 500 Hz

3.2 相干声源声功率反演

定义信噪比(Signal-to-noise ration,SNR)为

式(10)中：σm为测点m处接收到的背景干扰分量。对于图5(f)所示的声场分布，以(-10,0)为起点，按逆时针顺序每隔1 m取一个测点，构成一个50 m×50 m的矩形，测点分布如图5(f)中红色虚线所示。对测点处的声场加入信噪比为20 dB的背景噪声作为采样数据，使用两种代价函数分别进行100次蒙特卡洛仿真，参数反演结果如图6所示。其中图6(a)表示代价函数f的反演结果，图6(b)表示代价函数f2的反演结果。当使用代价函数f进行反演时，5个参数的估计结果均分布在真值附近，验证了反演方法的有效性。当使用代价函数f2进行反演时，尽管也能够得到相对准确的反演结果，但参数的集中程度较弱，说明基于绝对差值代价函数的抗误差能力较弱。对图6(a)的结果进行进一步的分析：使用表2中的声压系数参数，利用附录A中给出的声功率计算公式，可得电容器塔C1、电抗器L1的声功率级分别为132.13 dB和97.1 dB，而使用反演结果计算得到声功率估计值为132.13 dB(ˆwC=1.003)和95.36 dB(ˆwL1=0.49)。

图6 两种代价函数的反演结果对比Fig.6 Comparison of inversion results of two cost functions

3.3 实验数据分析

2021年3月，国网陕西省电力公司电力科学研究院的科研人员在驻马店±800 kV换流站内对交流滤波器组的噪声进行了现场测量。换流站内交流滤波器场的设备布置情况以及测点的分布情况如图7(a)所示，含两组三相滤波器，编号分别为5664和5663。图7(a)中黄色虚线表示围栏，尺寸为28 m×36 m×1.8 m。场内的电容器塔和电抗器实拍图像已由图2和图3给出。滤波器组5664的设备坐标见表1，坐标原点为滤波器组5664所在围栏的左下角。交流滤波器5663和5664的设备布置情况完全一致。因此5663的设备坐标可在5664的基础上沿x轴正向平移30 m得到(围栏间隔2 m)。测试期间，换流站工况保持恒定。实验中相邻两个测点的间距为1 m，每个测点处在高度为1.2 m和2.5 m高度上进行了两次测量。由于测点数量众多，受篇幅所限，这里仅统计了每个测点相对每个电容器塔和电抗器的距离分布，如图7(b)所示。可以看出，最小距离约为4 m，最大距离约为64 m，绝大部分测点距离大于10 m，均大于电抗器和电容器单元的最大尺寸。第一个测点的数据如图7(c)所示，在100 Hz、

图7 实验配置Fig.7 Experiment configuration

200 Hz、300 Hz、400 Hz、500 Hz、600 Hz、700 Hz、1100 Hz、1200 Hz、1300 Hz存在明显的线谱。

由于存在两组三相滤波器，因此待反演的参数包括：电抗器L1的声压系数wL1和相位φ1，电抗器L2的声压系数wL2和相位φ2，电容器的声压系数wC以及两组滤波器之间的相位差φ3。以500 Hz谱线为例，使用两种代价函数分别进行100次独立反演，统计反演结果的分布，结果如图8所示，其中图8(a)表示代价函数f的反演结果，图8(b)表示代价函数f2的反演结果。可以看出，当使用代价函数f进行反演时，声压系数参数的反演结果较为集中，而相位的反演结果较为分散，可以认为声压系数已收敛，而相位则没有收敛。当使用代价函数f2进行反演时，基本上所有参数的反演结果都很发散，说明此时已经无法获得正确的反演结果。进一步分析图8(a)的结果可知，ˆwC主要分布在0.005附近，ˆwL1主要分布在0.09附近，ˆwL2主要分布在0.05附近。由于相位并不影响计算单台设备的声功率计算，将ˆwC=0.005、ˆwL1=0.09、ˆwL2=0.05分别带入电抗器和电容器塔的声功率计算模型(见附录A)中，即可得到二者的声功率。电抗器L1和L2在500 Hz处的声功率级为80.6 dB和75.5 dB，电容器塔C1高压塔和低压塔的自由场声功率级均为86.1 dB。

图8 实验数据反演结果Fig.8 Inversion results using experiment data

为了验证反演参数的有效性，使用反演得到的参数对2.5 m处的声场进行预测，并与实验数据进行比较，结果如图9所示。尽管实测值与预测值在局部有一定的差异，但是总体上二者的趋势和量级上较为一致，这说明所采用等效声学模型很好地建模了相干声场的分布结构，间接说明了反演结果的有效性。此外，从量级上看，反演结果也具有一定的合理性。图9表明部分测点的噪声实测声压级已达到70 dB。如果以距离声源声中心1 m处的声压级为70 dB计算，对应的声功率级约为81 dB。由于测点与声源声中心的距离至少为4 m，对应的球面波传播损失为12 dB，考虑到地面按照镜反射估算约有6 dB增益，折算下来的声功率级约为87 dB。而文中通过反演得到的500 Hz处的电容器塔声功率级为86.1 dB，二者非常接近。这虽然是一个较为粗略的估算，仍在一定程度上说明反演结果是合理的。

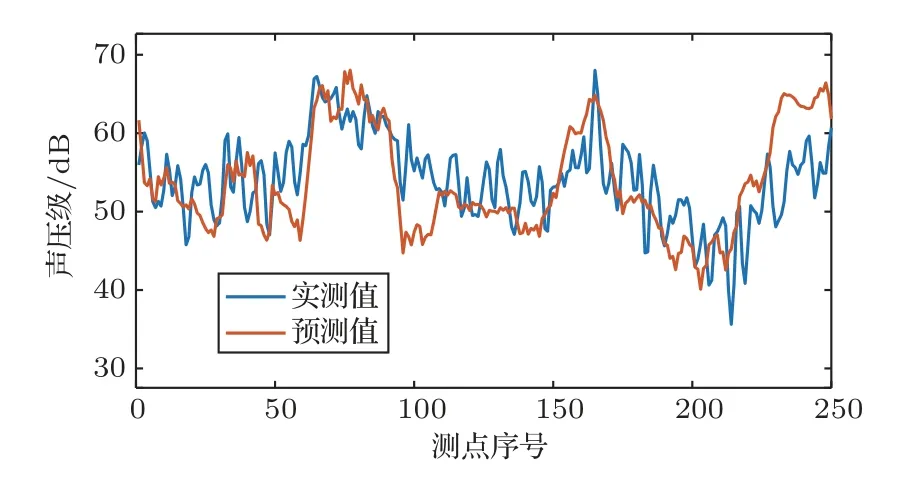
图9 实测值与预测值的比较(500 Hz)Fig.9 Comparison between measurements and predicted values(500 Hz)

4 应用条件与局限性分析

4.1 应用条件

在工程应用中，一个重要的问题是测点与场源(即电抗器、电容器单元)满足怎样的关系时才能保证反演方法的正确性。本文中声功率反演的准确性主要取决于所建立的等效声学模型对声源实际辐射特性的逼近程度。两者的逼近程度越好，则反演方法给出的声压系数估计值越准确，由此计算得到声功率自然越准确。

测点与场源距离。由于采用了点声源模型对场源进行近似，测点与场源之间距离至少需满足远场条件，才能保证点声源能够较好地模拟场源的声辐射特性。如果测点处于场源的近场区域，声场的幅度和相位随距离的变化较为剧烈，此时点声源模型无法模拟这种剧烈的变化，不再适用。以无限大障板上圆形活塞辐射声场为例，其近场和远场的临界距离为a2/λ，其中a表示活塞半径，λ表示声波波长。该条件同样适用于一般的辐射声源，此时可取a为最大尺寸的1/2。500 Hz时，电容器单元的最大声学尺寸以1 m计，对应的临界距离约为0.4 m；电抗器最大声学尺寸以2 m计，对应的近远场临界距离约为1.5 m。实验中的测点与场源之间最小距离为4 m，符合远场条件，可使用点声源来模拟此时的辐射特性。

测点数量。为了保证反演逆问题可解，测点数量的最低要求是不能小于反演参数的个数。例如，文中仿真部分对5个参数进行反演，则测点数量不应低于5个。在实际中，由于系统噪声、测量误差、模型误差等诸多因素的影响，仅使用最低数量的测点往往无法获得可靠的反演结果。从经验的角度而言，测量数量越多越好，且测点的位置分布尽可能多地采样声场空间分布。

测试条件。测试对象应尽可能远离其他强噪声源。此外，测量期间内，设备的运行工况应保持恒定。

4.2 局限性分析

由于采用了点声源近似，且换流站内测量空间受限，本文方法仅适用于中频段，具体频段受电容器单元以及电抗器具体尺寸、测点距离以及变电站实际环境的多重限制。随着频率的升高，波长越来越短，当波长小于噪声源设备时，点声源近似误差逐渐增大。波长减小也会导致近远场临界距离变大，现场条件不一定满足测点的测量条件。随着频率的降低，尽管点声源近似的精度升高，但是低频噪声的衰减较慢，测点声场受到换流站内其他大型设备强低频辐射噪声的污染影响较大。本文实验场景中测点与场源的最小距离为4 m，场源最大声学尺寸约为2 m，在近远场临界距离的约束下，上限频率约为1360 Hz(声速取340 m/s)。考虑到交流滤波器组周围存在大型变压器，500 Hz以下的低频辐射噪声较强，因此下限频率可取500 Hz。文献[2]指出，电容器单元的主要发声频率为100 Hz、500 Hz、600 Hz、700 Hz、1100 Hz、1200 Hz、1300 Hz。本文方法基本上覆盖了绝大部分频点。此外，本文没有考虑电容器和电抗器单元的辐射指向性，也没有考虑围栏、支撑结构引起复杂声学衍射。

5 结论

本文以几何声学理论为基础，结合交流滤波器场主要噪声源(电抗器与电容器塔)的声学特性，建立了交流滤波器场相干声场模型，并提出了声源参数的反演方法。仿真实验验证了反演方法的有效性。将该方法应用于驻马店±800 kV换流站内交流滤波器组的实测噪声数据，结果表明该方法可实现对相干声源的声压系数的有效反演。

该方法直接反演的是电容器塔和电抗器等效声源的声压系数，在此基础上进一步使用等效声源的声功率计算模型实现对声功率的间接反演，反演结果的精度依赖于等效声源模型的准确程度。对于工程应用而言，更关注的是噪声量级的整体分布情况，而无需获得过于精细的结果，因此对于模型的精度要求可适当放宽。本文采用了较为简单的点声源模型来近似电抗器和电容器单元，与交流滤波器场实际的声辐射特性难免存在差异。这种差异的存在使得在反演过程中不宜使用绝对量级来衡量模型预测声场和实测声场的接近程度，因此本文使用了相关系数为衡量标准，由此得到的反演结果与实验数据展现出较好的一致性。

在接下来的研究中，可将电抗器和电容器单元的辐射指向性考虑在内，进一步提高声场建模的准确度，并研究衡量模型预测声场和实测声场接近程度的不同标准对反演结果的影响，以进一步提高反演结果的准确度。

附录A

在本文中，电抗器的声功率计算公式为

式(A1)中：A表示声压系数，ρ表示空气密度，c表示空气中的声速。电容器塔的声功率计算公式为

式(A2)中：k表示声波的波数，Nx、Ny、Nz分别表示x轴、y轴、z轴方向上电容器单元的个数；dx、dy、dz分别表示x轴、y轴、z轴方向上电容器单元声学中心的间距。