抑制风噪装置的实验

吴 睿 金向锋

(惠州迪芬尼声学科技股份有限公司 惠州516000)

0 引言

随着主动降噪(Active noise control,ANC)技术的成熟，真无线立体声(True wireless stereo,TWS)ANC耳机成为研究热点[1-3]。ANC的基本原理为对系统中的前馈传声器和后馈传声器拾取到的噪声进行数字信号处理(Digital signal processing,DSP)，用处理后的信号激励扬声器，使其发出反相的噪声来实现降噪。大多数环境噪声会在该机理下被降低，但是在风速较大的环境中ANC效果不佳。风速较大时传声器会拾取到风噪，由于风噪信号不属于线性时不变(Linear time-invariant systems,LTI)系统，ANC机理对其无效。因此有必要研究如何抑制传声器拾取风噪信号。从膜片接收到声波的方式，可将传声器分成“纯粹压力式”和“有压差式存在”两大类。前者可拾取全方向的声波，后者可根据压差成分比例设计需要的指向性。本文研究如何抑制全指向性传声器拾取风噪。

传声器拾取风噪的原理涉及流体力学，实际上风噪并不是风声信号，而是传声器采集到了空气湍流所引起的传声器膜片扰动。对抑制传声器拾取风噪的研究，可追溯到20世纪80年代。Strasberg[4]提出利用置于传声器外部的声屏障结构来抑制风噪。通过量纲分析讨论了抑制风噪的影响因素，包括风速、声屏障大小和形状。并利用公式(1)来计算传声器拾取到的风噪大小。

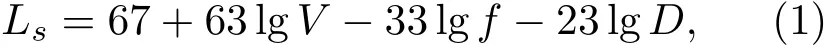
式(1)中，V是流速，f为频率，D是声屏障的直径。

但Strasberg的研究只限于风速较低的情况。Morgan等[5]研究了高流速下，风噪形成的原因。根据伯努利理论，提出层流中的压力波动与流体的动能有关。在高流速下，空气中的总气压为

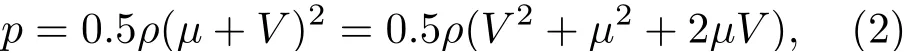
其中，μ是波动速度，V是平均流速，ρ是气体密度。高流速下，波动速度为平均速度的5%～15%，所以公式(2)的值主要由第三项决定，即p=ρμV。因此Morgan等认为高流速下，风噪主要来源于气流中的湍流压力扰动；并通过实验得出，流速较高时声屏障并不能有效地减弱风噪。van den Berg[6]分别对低流速和高流速条件下的风噪进行了研究。他提出低流速下，传声器拾取到的风噪主要来源于气流与风屏障作用产生的涡流；而高流速下，风噪来自于气流中本身的湍流。声屏障在低流速下，对风噪有较好的抑制作用；但是在高流速下，它的效果并不显著。

目前应用的抑制传声器拾取风噪的结构，大都没有根据上述原理进行设计，效果欠佳。例如在传声器的拾声孔前加一段管道[7-9]。单独管道并不会抑制风噪，反而会由于管壁的黏滞效应增大气流中的涡流，从而使风噪增强。另一种设计是腔体在前管道在后的抗风噪结构[10-11]，气流从腔体到管道，横截面变小流速会加快，因此风噪也会增大。此外还有小孔加腔体的设计结构[12]，虽然在低流速会降低风噪，但是高流速下效果不佳。同时这种设计并没有考虑到腔体引起的声波传递损失。

为了简化分析，本文忽略来风方向进行研究。基于风噪原理提出一种抗风噪结构设计，来抑制TWS耳机中全指向性传声器拾取风噪。然后进行有限元仿真和风噪实验，验证设计结构的抗风噪能力。最后，基于声波的传递损失特性提出结构的尺寸设计指标，保证传声器拾取的声信号不会在高频失真。

1 抗风噪结构设计

目前TWS耳机中常用的微机电系统(Microelectro-mechanical Systems,MEMS)电容式全指向性传声器如图1所示，其长、宽、高分别为3 mm、2 mm和1 mm左右。其拾声孔的直径一般为0.5 mm。由传声器拾取风噪的原理可知，低流速下声屏障对风噪有较好的抑制作用，但是高流速下效果甚微。所以本文设计的抗风噪结构由两部分组成，第一部分降低气流流速，第二部分充当声屏障，如图2所示。

图1 MEMS传声器Fig.1 MEMS transducer

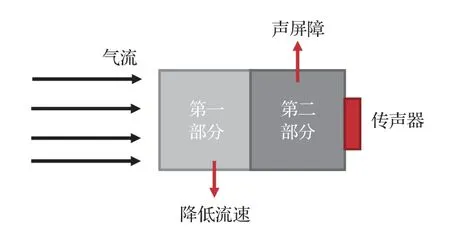
图2 设计结构示意图Fig.2 The schematic diagram of the designed structure

1.1 降低流速

第一部分的设计结构为渐变管道，从气流入口到传声器的方向横截面逐渐增大。考虑到TWS耳机的空间大小，管道的直径在0.6～1.2 mm之间，长度在5 mm以内。由于管道直径较小，管壁会与大部分气流发生强烈的黏滞反应[5]，从而耗散气流动能并降低气流流速[13]。其次，根据物质守恒原理，理想条件下管道每个截面的气流量相同，如公式(3)所示：

其中，V和S分别代表管道某截面的流速和面积。显然截面积越大，气流流速越小。因此，开口逐渐增大的管道会降低气流流速。

基于有限元仿真，验证该设计管道对气流流速的影响。模型使用“湍流，k-ε”接口求解渐变管道中的气流湍流，并采用含壁函数的湍流模型与对称面边界条件来简化计算。仿真模型中的渐变管道长度为3 mm，气流入口面直径为0.6 mm，出口面直径为1 mm。入口面处入射气流流速设定为10 m/s。仿真结果如图3所示，不同颜色代表了不同的流速，气流经过管道后，流速衰减明显。图4展示了管道出口截面的流速分布图，出口截面中流速均低于5 m/s。而且速度分布符合黏滞效应，靠近管壁流速低，管道中部流速高。因此，仿真结果验证了截面逐渐变大的直管能有效地降低气流流速这一结论。考虑到实际结构的可制作性与一致性，弯管不在本文的讨论范围中。但根据原理，截面逐渐增大的弯管也能有效地降低气流流速。

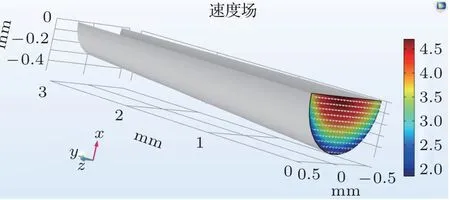
图4 出口横截面的流速分布Fig.4 Velocity distribution on outlet cross section

1.2 声屏障

第二部分结构为腔体，腔体内填充泡棉，充当抑制风噪的声屏障。整体抗风噪设计结构如图5和图6所示，气流先通过渐变管，从高流速转变为低流速。在低流速状态下，气流再经过声屏障，最后到达传声器的拾声孔。由公式(1)可知，声屏障的面积越大，抑制风噪的效果越好。因此泡棉设计为尖劈形，增大与气流的接触面积。

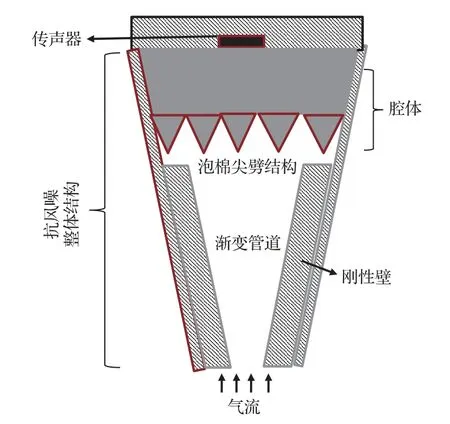
图5 整体结构示意图Fig.5 Overall structure diagram

图6 整体结构实物图Fig.6 Overall real structure

2 抑制风噪的实验

2.1 对比实验

基于该设计结构进行风噪测试实验。实验时传声器正对风管，采集传声器所拾取到的风噪信号。实验采用的MEMS传声器尺寸为2.7 mm×1.8 mm×1 mm，灵敏度-38 dBV/Pa，信噪比64 dB(A)。传声器和设计结构按图6方式固定。风管提供流速为10 m/s的气流，实验时结构固定在支架上，与风管出口距离30 cm，如图7所示。采用Audio Precision 5.0声频测量设备，录取传声器拾取到的信号并进行分析。

图7 实验示意图Fig.7 Wind noise experiment setup

进行对比实验，抗风噪测试的对象如下：(1)单独传声器；(2)传声器前加一段直管；(3)传声器前加抗风噪结构。同一对象录声5次，对频谱结果进行平均处理来减少实验误差。实验结果如图8所示。和单独传声器相比，抗风噪结构能明显减弱传声器拾取到的风噪，而且频率越高效果越好。在人听感最明显的频率点1000 Hz，能抑制10 dB左右的风噪。

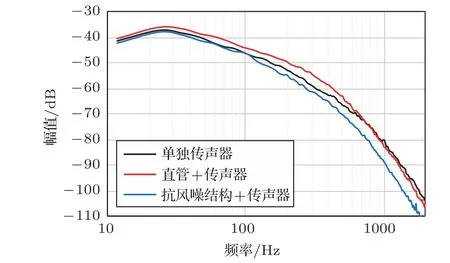
图8 对比实验结果Fig.8 Results of the comparison experiments

直管结构不仅不会抑制风噪，反而会增大风噪。虽然直管由于管壁的黏滞效应降低了气流的流速，但是在其出口处截面存在明显的速度梯度，如图4仿真模型中管道出口的速度分布。速度梯度是形成湍流的重要原因。因此直管出口处湍流剧烈，传声器采集到的风噪信号不降反增。

2.2 影响因素

对该抗风噪结构的几个关键因素进行实验分析。包括腔体大小、管道等效直径和泡棉材质。首先保持其他条件相同，采用大小分别为3.6 mm×2.4 mm×3.1 mm和8.33 mm×7.7 mm×4.5 mm的两种腔体组装成抗风噪结构，进行对比实验。图9实验结果表明了大腔体有更好的抑制风噪能力，尤其在中高频效果更明显。其本质是因为大腔体增大了声屏障与气流的接触面积。

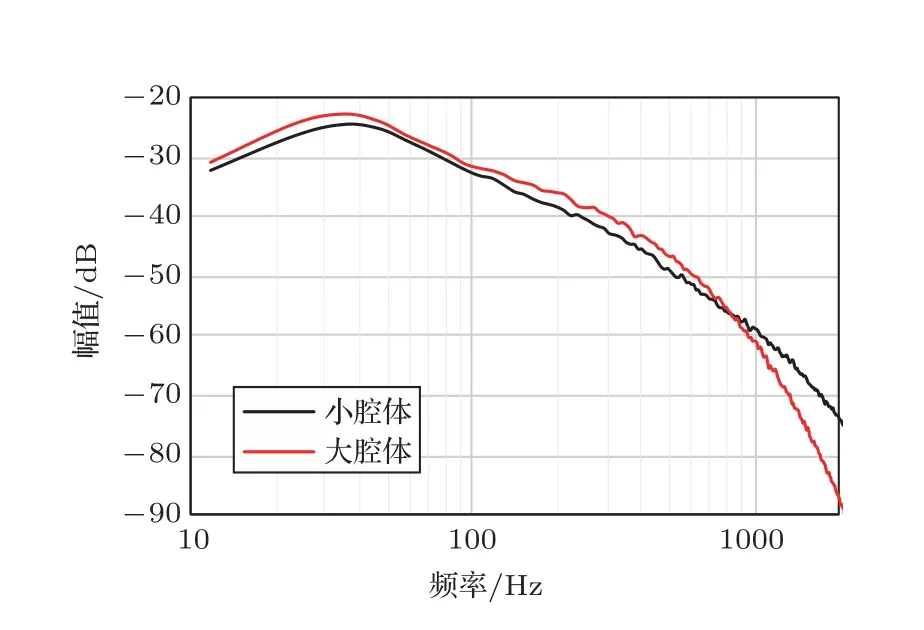
图9 不同大小腔体的抗风噪实验结果Fig.9 Experiment results of different cavities

图10展示了不同等效直径的渐变管所构成的抗风噪结构的效果对比。等效直径定义为d=L/π，其中L为管道中心(距离入口为管道总长度一半的位置)的截面周长。等效直径越小，抗风噪性能越好。管道越小，管壁黏滞效应会和更多的气流发生反应，亦会更有效地消耗能量降低流速。图11展示了3种不同密度的泡棉，将其装入腔体组成结构进行实验。对比结果如图12所示。泡棉密度越大，抗风噪效果越好。从原理上分析，泡棉密度越大，泡棉孔隙率越小，声屏障和气流的接触面积越大。

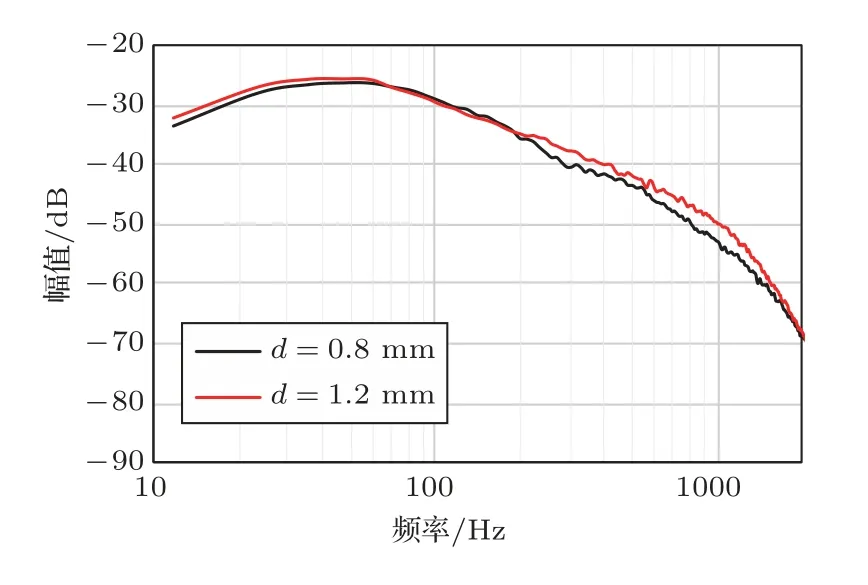
图10 不同管道直径的抗风噪实验结果Fig.10 Experiment results of different tube diameters

图11 3种不同密度的泡棉Fig.11 Three different kinds of foams

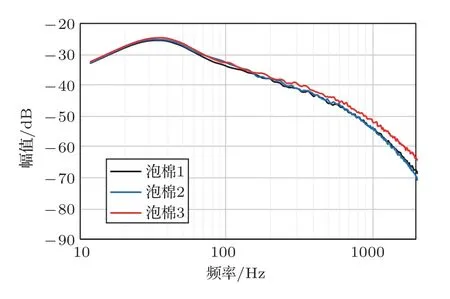
图12 不同密度泡棉的抗风噪实验结果Fig.12 Experiments results of different foams

3 声波传递损失分析

抗风噪结构帮助传声器抑制风噪的同时，也要保证其他有用声信号通过，例如人声。根据声传输线以及等效电路理论[14]，该传播路径可以等效为图13所示电路。由声质量Ma和声容Ca组成一个低通滤波器。其截止频率和相关参数如公式(4)和公式(5)所示：

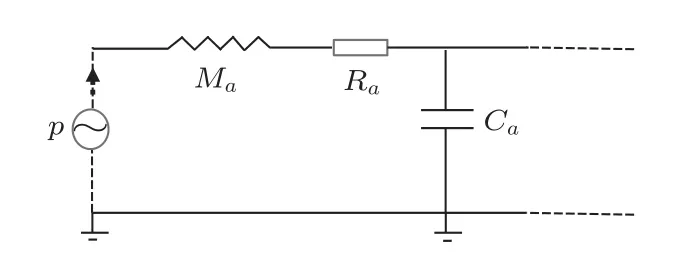
图13 等效电路图Fig.13 The equivalent circuit

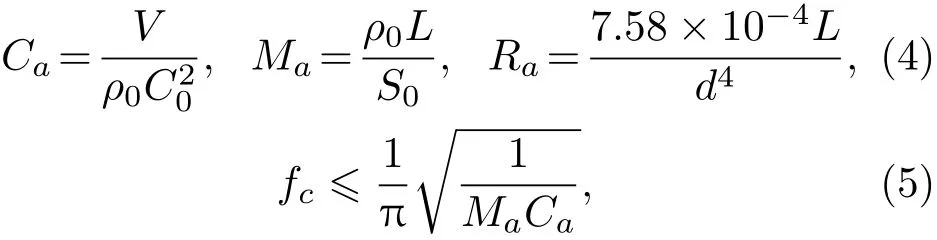
其中，Ra为管道的声阻，简化模型忽略腔体和泡棉的阻抗；V是结构中腔体的体积，d为管道的等效直径，ρ0是空气密度，c0是空气中的声速，L是设计管道的长度，S为管道的横截面积。

基于不同尺寸的抗风噪结构，进行声波传递损失实验。以截止频率评价其效果，显然截止频率越低，传递损失越大。传声器和不同参数的结构耦合，如图7固定在支架上，两种结构参数如表1所示。内部均填充密度为18 kg/m3的相同泡棉。同时根据公式(4)和公式(5)计算出两种结构下的理论截止频率，见表1。在消声室中音箱发出50～10000 Hz的扫频信号，Audio Precision 5.0声频测量设备录取并分析传声器拾取到的信号。

表1 实验结构参数Table 1 The parameters of two different structures

图14展示了实验结果。和单独传声器曲线相比，可得两种结构的实测截止频率分别在5000 Hz和1000 Hz左右，基本和表1中的理论截止频率吻合。因此该等效电路模型能较准确地计算抗风噪结构的声波传递截止频率。

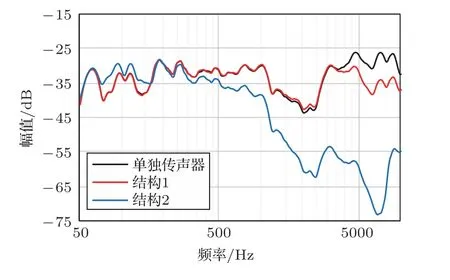
图14 传递损失实验结果Fig.14 Results of the transmission loss experiment

对于该设计结构，存在本征固有频率。系统的Q值大于时结构会强烈的共振，从而产生“哨声”。为了避免该现象，系统的Q值应小于，如公式(6)所示。进一步化简得到公式(7)，抗风噪结构的设计需满足该式。

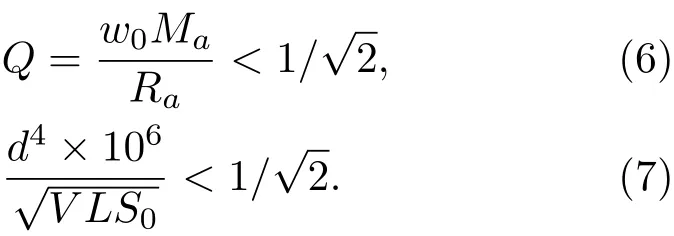
为了保证耳机有良好的通话功能，传声器至少需要在8000 Hz以内拾取到不失真的声音，所以低通截止频率应大于8000 Hz，如公式(8)所示。结合公式(4)和公式(5)，可得公式(9)：

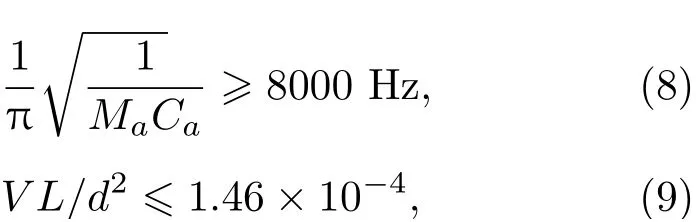
其中，d和L分别为渐变管的等效直径和长度，V为腔体的体积。对于抗风噪结构，大的腔体体积、小的管道等效直径和长的管道长度L都利于抗风噪性能，但是三者间的关系需要满足式(9)，才能保证传声器拾取到的高频信号不失真。因此，公式(7)和公式(9)为抗风噪结构的尺寸设计指标。

4 结论

本文首先介绍了传声器拾取风噪的原理，并分析了目前应用的抗风噪结构的设计缺陷。然后基于风噪原理，提出了一种新型抗风噪结构设计，来抑制传声器拾取风噪。

该设计由渐变管道和填充泡棉的腔体两部分组成。渐变管道用来降低气流的流速，填充泡棉的腔体用来充当声屏障。基于有限元仿真，验证了渐变管道降低流速的能力。风噪实验结果证明了该设计能有效地抑制风噪。但是单独直管结构对传声器拾取到的风噪不增反降。

讨论了几个关键因素对该结构抗风噪能力的影响。大的腔体、小的渐变管等效直径和高的泡棉密度，都有利于结构的抗风噪效果。最后，基于声传输线和等效电路理论，建立了声波经过该抗风噪结构的传递损失模型，并通过实验验证了其准确性。基于该模型和高频不失真条件，提出了抗风噪结构的尺寸设计指标。